Weiterbildung Informatik
Inhaltsverzeichnis
Sekundarstufe I
1. Visuelle Programmierung
- 1.1 Visuelle Programmierung
- 1.2 Einstieg in Scratch
- 1.2.1 Übungsaufgaben
- 1.3 Kontrollstrukturen
- 1.3.1 Übungsaufgaben
- 1.4 Programmieren mit Variablen
- 1.4.1 Übungsaufgaben
- 1.5 Strukturierung von Programmen
- 1.5.1 Übungsaufgaben
- 1.5.2 Vertiefung
- 1.6 Anhang
- 1.6.1 Scratch-Referenz
2. Informationsdarstellung
- 2.1 Informationsdarstellung
- 2.2 Codierung digitaler Daten
- 2.2.1 Codierung von Textdaten
- 2.2.2 Codierung von Bilddaten
- 2.2.3 Grafische Codes
- 2.2.4 Datenkompression
- 2.3 Informationsdarstellung im Internet
- 2.3.1 Strukturierung mit HTML
- 2.3.2 Gestaltung mit CSS
3. Algorithmik
- 3.1 Einstieg in die Algorithmik
- 3.1.1 Übungsaufgaben
- 3.2 Darstellung von Algorithmen
- 3.2.1 Übungsaufgaben
- 3.3 Anhang
4. Netzwerke & Internet
- 4.1 Netzwerke und Internet
- 4.2 Kommunikationsprotokolle
- 4.3 Netzwerke
- 4.4 Kommunikation im Netzwerk
- 4.5 Anwendungsprotokolle
5. Programmierung in Python
- 5.1 Programmierung in Python
- 5.2 Einstieg in Python
- 5.3 Variablen und Ausdrücke
- 5.4 Funktionen und Bibliotheken
- 5.4.1 Die datetime-Bibliothek
- 5.5 Kontrollstrukturen
- 5.6 Debugging
- 5.7 Datenstrukturen
- 5.8 Objekte
6. Links
- 6.1 Materialsammlungen
- 6.2 Software-Werkzeuge
Sekundarstufe II
7. Blick über die Informatik
8. Algorithmen
9. Grundlagen der Programmierung
- 9.1 Arithmetische Ausdrücke und Variablen
- 9.2 Weitere primitive Datentypen
- 9.2.1 Übungsaufgaben
- 9.3 Bedingte Anweisungen
- 9.3.1 Übungsaufgaben
- 9.4 Schleifen
- 9.4.1 Übungsaufgaben
- 9.5 Programmablaufplan (PAP)
- 9.5.1 Übungsaufgaben
- 9.6 Tabellarische Programmausführung
- 9.6.1 Übungsaufgaben
- 9.7 Zusammenfassung, Quellen und Lesetipps
- 9.8 Lösungen
10. Programmiertechniken
- 10.1 Aufzählen und Überprüfen
- 10.1.1 Übungsaufgaben
- 10.2 Teilen und Herrschen
- 10.2.1 Übungsaufgaben
- 10.3 Vertiefung
- 10.3.1 Übungsaufgaben
- 10.4 Quellen und Lesetipps
- 10.5 Lösungen
11. Funktionen und Prozeduren
- 11.1 Abstraktion von Ausdrücken durch Funktionen
- 11.1.1 Übungsaufgaben
- 11.2 Benutzereingaben verarbeiten
- 11.2.1 Übungsaufgaben
- 11.3 Abstraktion von Anweisungen durch Prozeduren
- 11.3.1 Übungsaufgaben
- 11.4 Lösungen
12. Programmierung mit Zeichenketten
- 12.1 Programmierung mit Zeichenketten
- 12.1.1 Aufgaben
- 12.2 Suche in Zeichenketten
- 12.3 Lösungen
13. Programmierung mit Listen
- 13.1 Programmierung mit Listen
- 13.1.1 Aufgaben
- 13.2 Suche in Listen
- 13.2.1 Aufgaben
- 13.3 Lösungen
14. Programmierung mit Dictionaries
- 14.1 Dictionaries
- 14.1.1 Aufgaben
- 14.2 Tupel
- 14.3 Sets
15. Terme und ihre Auswertung
- 15.1 Termdarstellungen
- 15.1.1 Aufgaben
- 15.2 Schlangen und Keller
- 15.3 Termauswertung einer Stackmaschine
- 15.3.1 Aufgaben
- 15.4 Tabellenkalkulation
- 15.4.1 Aufgaben
- 15.5 Lösungen
16. Reguläre Ausdrücke
17. Syntaxbeschreibung mit (E)BNF
- 17.1 Syntax arithmetischer Ausdrücke
- 17.1.1 Aufgaben
- 17.2 Syntax von Palindromen
- 17.3 Erweiterte Backus-Naur-Form (EBNF)
- 17.4 Syntax von Python-Anweisungen
- 17.4.1 Aufgaben
- 17.5 Lesetipps
- 17.6 Lösungen
18. Rekursion
- 18.1 Rekursive Funktionen
- 18.1.1 Aufgaben
- 18.2 Rekursive Prozeduren
- 18.2.1 Aufgaben
- 18.3 Rekursion und Schleifen
- 18.4 Die Türme von Hanoi
- 18.4.1 Aufgaben
- 18.5 Lösungen
19. Sortieren und Effizienz
- 19.1 Einfache Sortierverfahren und ihre Laufzeit
- 19.1.1 Aufgaben
- 19.2 Insertion Sort
- 19.2.1 Aufgaben
- 19.3 Systematische Laufzeitanalyse
- 19.4 Effizientere Sortierverfahren
- 19.4.1 Aufgaben
- 19.5 Lösungen
20. Objekte und ihre Identität
- 20.1 Mutation
- 20.1.1 Aufgaben
- 20.2 Objekt-Identität
- 20.3 Weitere Mutations-Anweisungen
- 20.3.1 Aufgaben
- 20.4 Mutation als Seiteneffekt
- 20.4.1 Aufgaben
- 20.5 Lösungen
21. Definition von Objekten
- 21.1 Rationale Zahlen als Objekte
- 21.1.1 Übungsaufgaben
- 21.2 Mutierbare Objekte
- 21.2.1 Übungsaufgaben
- 21.3 Lösungen
22. Hierarchische Modularisierung
- 22.1 Aggregation
- 22.2 Vererbung
- 22.2.1 Übungsaufgaben
- 22.3 Dynamische und späte Bindung
- 22.4 Ersetzbarkeitsprinzip
- 22.4.1 Übungsaufgaben
- 22.5 Lösungen
23. Rechnerarchitektur
- 23.1 Schaltnetze
- 23.1.1 Übungsaufgaben
- 23.2 Synchrone Schaltwerke
- 23.3 Hauptprozessor und Von-Neumann-Architektur
- 23.4 Assembler
- 23.5 Quellen und Lesetipps
- 23.6 Lösungen
24. Netzwerke
- 24.1 Netzwerkdienste und -protokolle
- 24.1.1 Übungsaufgaben
- 24.2 Internet
- 24.2.1 Übungsaufgaben
- 24.3 Die HyperText Markup Language (HTML)
- 24.3.1 Übungsaufgaben
- 24.4 Quellen und Lesetipps
- 24.5 Lösungen
25. Dynamische Webseiten
- 25.1 HTML-Formulare für Benutzereingaben
- 25.2 Client-seitige Webprogrammierung mit Javascript
- 25.2.1 Übungsaufgaben
- 25.3 Das Document Object Model (DOM)
- 25.3.1 Übungsaufgaben
- 25.4 Lösungen
26. Digitale Bildverarbeitung
- 26.1 Rastergrafiken und Histogramme
- 26.1.1 Übungsaufgaben
- 26.2 Bildverarbeitung in Python
- 26.2.1 Übungsaufgaben
- 26.3 Quellen und Lesetipps
- 26.4 Lösungen
27. Backtracking
- 27.1 Suchbäume
- 27.2 Damenproblem
- 27.3 Aufgaben und Lösungen
28. Künstliche Intelligenz für Spiele
- 28.1 Zwei-Personen-Spiele und automatisches Spiel
- 28.1.1 Aufgaben
- 28.2 Bewertung von Spielzügen
- 28.2.1 Aufgaben
- 28.3 Lösungen
- 28.3.1 Lösungen
29. Neuronale Netze
- 29.1 Das Perzeptron
- 29.2 Training vernetzter Neuronen
- 29.3 Programmierung Neuronaler Netze mit Keras
30. Relationale Datenbanken
31. Algorithmen und Datenstrukturen
- 31.1 Hashing
- 31.2 Python-Listen
- 31.3 Definition Suchbäume
32. Datenbankprogrammierung in Python
33. Webprogrammierung in Python
34. Verteilte Versionskontrolle
Sekundarstufe I
1. Visuelle Programmierung
1.1 Visuelle Programmierung
Einleitung
In diesem Modul werden Sie anhand der Programmiersprache Scratch in die Grundlagen der Programmierung eingeführt.
Scratch ist eine visuelle Programmiersprache inklusive einer Entwicklungsumgebung (engl. integrated development environment oder IDE), die von der Lifelong Kindergarten Group am MIT Media Lab entwickelt wurde und unter didaktischen Gesichtspunkten für Kinder und Jugendliche konzipiert ist. In visuellen Programmiersprachen werden Programme im Gegensatz zur textbasierten Programmierung aus grafisch gestalteten Elementen nach dem “Baukastenprinzip” zusammengesetzt, deren Bedeutung über ihre visuelle Repräsentation (Form, Farbe und Beschriftung) intuitiv erschlossen werden kann. Im Vordergrund steht die einfache Bedienbarkeit.
Visuelle Programmierungsprachen vermeiden so, dass eine komplizierte, abstrakte Syntax gelernt und eingehalten werden muss und ermöglichen einen spielerischen und explorativen Zugang zum Programmierenlernen.1 Scratch und verwandte visuelle Programmiersprachen wie Blockly, NEPO, MakeCode oder Snap! haben sich als Einstieg in die Programmierung im Informatikunterricht bewährt und stellen in ihren Online Communities umfangreiches didaktisch aufbereitetes Material für den Informatikunterricht zur Verfügung (siehe Materialsammlung). Ausgewählte Unterrichtsmaterialien werden auch im Rahmen der Weiterbildung behandelt.
Vorbereitung
Scratch-Projekte lassen sich direkt im Webbrowser oder auf Ihrem Rechner mit der Desktop-Anwendung Scratch-App erstellen. Am einfachsten ist die Verwendung der Browserversion, hierzu benötigen Sie aber eine laufende Internetverbindung, während Sie arbeiten.
Wenn Sie lieber offline arbeiten möchten oder sicherstellen möchten, dass keine persönlichen Daten übermittelt werden2, installieren Sie als Erstes die Desktop-Anwendung auf Ihrem Arbeitsrechner.
Scratch als Desktop-Anwendung
Die Scratch-App wird auf Ihrem Rechner installiert und läuft dort dann auch ohne Internetverbindung. Scratch-Projekte werden lokal auf Ihrem Rechner gespeichert und von dort geladen.
Die Installationsdatei kann von der Scratch-Homepage unter https://scratch.mit.edu/download heruntergeladen werden. Als Betriebssysteme werden momentan Windows 10, macOS (ab Version 10.13), sowie ChromeOS und Android für Tablets unterstützt.
Wenn Sie ein Linux-System verwenden, können Sie auf die inoffizielle Linux-Portierung Scratux ausweichen, die Sie über den Snap Store oder über die Projekt-Homepage https://scratux.org installieren können.
Nachdem Sie die Scratch-App gestartet haben, sollten Sie das Fenster als Erstes maximieren und als Sprache “Deutsch” für die Oberfläche über das Symbol  in der Menüleiste auswählen.
in der Menüleiste auswählen.
Scratch im Webbrowser
Öffnen Sie in Ihrem Webbrowser die Seite https://scratch.mit.edu/projects/editor, um direkt im Webbrowser Scratch-Projekte zu erstellen und abzuspielen.
Die Browserversion von Scratch bietet denselben Umfang wie die Desktop-Anwendung und kann auch verwendet werden, ohne einen Account zu registrieren.
Account registrieren
Die Registrierung eines Accounts bietet den Vorteil, dass Sie Ihre Projekte zusätzlich online speichern und veröffentlichen können. Mit einem Account für Lehrkräfte können Sie darüber hinaus Accounts für Ihre Schülerinnen und Schüler anlegen und in Klassen verwalten.
Mit einem Lehrkräfte-Account können Sie auch gemeinsam nutzbare Ressourcen-Pools (“Lager”) anlegen, über die Programmcode, Grafiken und Sound-Effekte innerhalb der Klassen ausgetauscht werden können, sowie “Studios”, in denen die Schülerinnen und Schüler ihre erstellten Projekte innerhalb der Klasse veröffentlichen können.
Weitere Informationen zum Anlegen und Nutzen eines Lehrkräfte-Accounts finden Sie auf der Scratch-Homepage unter https://scratch.mit.edu/educators.
Scratch-Projektdateien
Ein Scratch-Projekt kann über das Dateimenü der Scratch-Oberfläche lokal in einer Datei mit der Endung .sb3 gespeichert und daraus geladen werden. Eine Projektdatei enthält immer alle Skripte und Ressourcen (also Grafiken und Soundeffekte), die im Projekt verwendet werden.
In der browserbasierten Version von Scratch lassen sich Projekte auch online speichern, wenn Sie einen Account registriert und sich darin angemeldet haben.
Beachten Sie, dass wir in der Weiterbildung ausschließlich mit Version 3 von Scratch arbeiten werden. Projektdateien älterer Scratch-Versionen können mit Scratch 3 aber in der Regel auch geöffnet werden.
-
siehe auch Peer Stechert: Kriterien zur Auswahl einer Programmiersprache – Bsp. Scratch aus der Reihe Informatikdidaktik kurz gefasst (Teil 31), Video bei YouTube ↩︎
-
Beachten Sie dazu auch die Datenschutzbestimmungen von Scratch. ↩︎
1.2 Einstieg in Scratch
Zu Beginn werden Sie als Einstieg in die visuelle Programmierung die Handhabung der Scratch-Entwicklungsumgebung kennenlernen und erste kleine Projekte erstellen.
Dabei werden Sie die ersten grundlegenden Programmierkonzepte kennenlernen: Die Konstruktion von Programmen aus elementaren Anweisungen und Anweisungssequenzen, hier um Objekte zu steuern und Reaktionen auf bestimmte Ereignisse festzulegen.
Grundlagen
In einem Scratch-Projekt agieren Spielfiguren in einer 2D-Welt, die in Scratch als “Bühne” bezeichnet wird. Figuren werden durch Bilder dargestellt, ihr “Kostüm”. Das Verhalten und Aussehen der Figuren lässt sich mit Hilfe von kleinen Bausteinen steuern, den “Blöcken”. So lassen sich mit einzelnen Blöcken beispielsweise Figuren bewegen, das Bild einer Figur wechseln, Soundeffekte abspielen oder auf der Bildschirmfläche zeichnen, wobei jeder Block eine andere elementare Anweisung repräsentiert. Blöcke können wie Puzzleteile zu komplexeren Steuerungsvorschriften zusammengesetzt werden, den “Skripten”.
Um von der “Theater-Metapher”, die Scratch verwendet, zu abstrahieren, werden Figuren im Folgenden allgemeiner als “Objekte” bezeichnet. Statt “Bühnenbild” oder “Kostüm” werden die Bilder, die zur Darstellung von Objekten und Hintergrund verwendet werden, hier allgemeiner als “Grafik” bezeichnet.
 |
Die Benutzeroberfläche
Die Oberfläche der Entwicklungsumgebung von Scratch ist im Entwurfsmodus in die folgenden Bereiche aufgeteilt:
-
Über die obere Menüleiste können Sie Projekte laden und speichern (Menüpunkt “Datei”), die Sprache der Entwicklungsumgebung wählen (Symbol
 ) und Tutorialvideos zu verschiedenen Themen ansehen.
) und Tutorialvideos zu verschiedenen Themen ansehen. -
Auf der linken Seite befindet sich der Arbeitsbereich. In diesem Bereich wird das momentan ausgewählte Objekt (Figur oder Bühne) bearbeitet. Über die Reiter lässt sich zwischen den verschiedenen Bereichen für Skripte, Grafiken und Soundeffekte des Objekts wechseln.
-
Auf der rechten oberen Seite befindet sich das Vorschaufenster des erstellten Programms, das den Bühnenbereich und die darin befindlichen Figuren darstellt. Das Programm kann jederzeit in der Vorschau durch Klicken auf die grüne Fahne
 ausgeführt werden. Mit einem Klick auf das Symbol
ausgeführt werden. Mit einem Klick auf das Symbol  oben rechts wird in den Präsentationsmodus gewechselt, in dem das Programm im Vollbild ausgeführt werden kann.
oben rechts wird in den Präsentationsmodus gewechselt, in dem das Programm im Vollbild ausgeführt werden kann. -
Unterhalb des Vorschaufensters befindet sich die Objektliste mit allen im Projekt vorhandenen Objekten, also Figuren und Bühne. Wählen Sie hier ein Objekt per Mausklick aus, um es im Arbeitsbereich zu öffnen. Mit einem Rechtsklick auf eine Figur können Sie diese löschen oder eine Kopie erzeugen. Dabei werden auch alle Skripte, Grafiken und Soundeffekte der Figur kopiert.
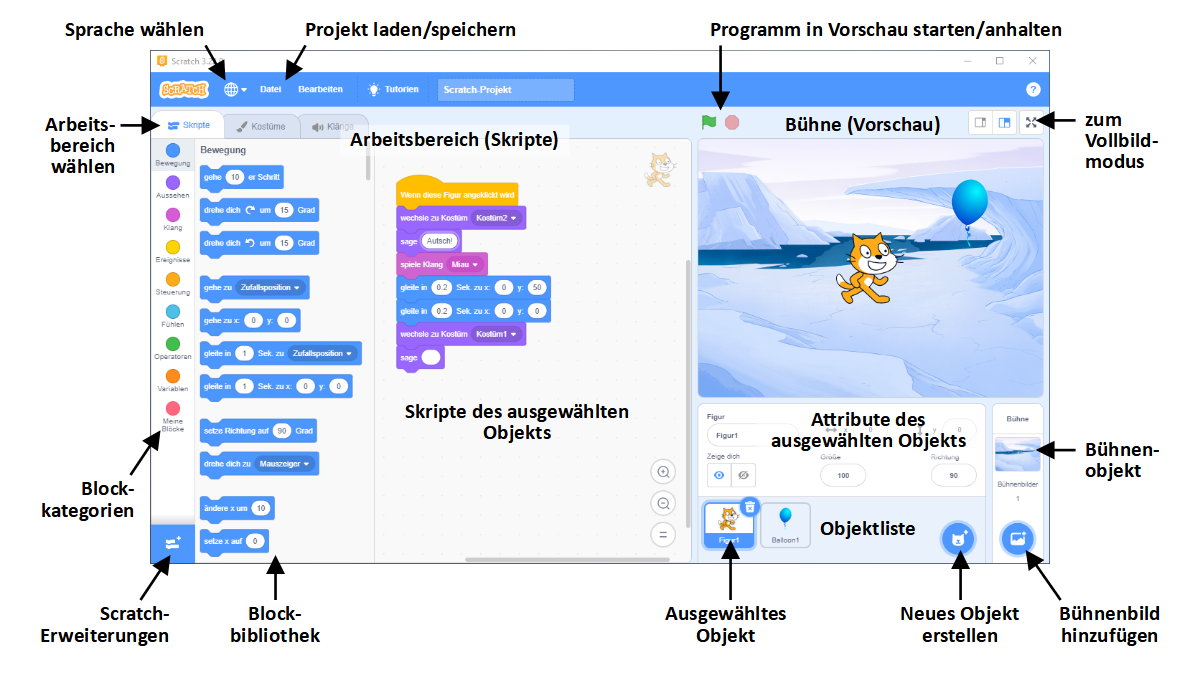
Das Verhalten jedes Objekts kann individuell durch Skripte programmiert werden. Auch das Verhalten der Bühne kann durch Skripte gesteuert werden. Wählen Sie den Reiter  “Skripte” des Arbeitsbereichs, um den Skriptbereich der momentan ausgewählten Figur oder der Bühne zu öffnen.
“Skripte” des Arbeitsbereichs, um den Skriptbereich der momentan ausgewählten Figur oder der Bühne zu öffnen.
Auf der linken Seite des Skriptbereichs finden Sie die Block-Bibliothek (auch als “Block-Palette” bezeichnet). Hier sind die Programmier-Bausteine oder “Blöcke”, aus denen Skripte zusammengestellt werden, in verschiedene, farblich unterschiedlich gekennzeichnete Kategorien aufgeteilt. Die Kategorien beziehen sich auf verschiedene Programmieraspekte, auf welche die entsprechenden Blöcke Einfluss haben, z. B. Bewegung von Objekten, Steuerung der Objektgrafik oder Soundeffekte.
Der mittlere Bereich enthält die Skripte, die zum ausgewählten Objekt gehören. Erstellen Sie Skripte, indem Sie Blöcke aus der Bibliothek mit der Maus in die Arbeitsfläche ziehen und miteinander kombinieren. Mit einem Rechtsklick auf einen einzelnen Block oder einen Verbund von Blöcken können Sie diesen löschen oder kopieren.
🎓 Erste Schritte
Öffnen Sie ein neues Scratch-Projekt. Zu Beginn befindet sich auf der Bühne ein einzelnes Objekt namens “Figur1” (das Scratch-Maskottchen), das ausgewählt ist.
Zunächst werden wir uns auf Anweisungen aus den ersten drei Kategorien konzentrieren:
| “Bewegung” (blau) | “Aussehen” (violett) | “Klang” (pink) |
|---|---|---|
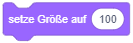
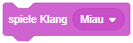
| Steuerung der Position und Drehung von Objekten, zum Beispiel: | Steuerung der Grafik (“Kostüm”-Wahl, Grafikeffekte, Sichtbarkeit und Größe) und Textausgabe (“Sprechblasen”) für Objekte, zum Beispiel: | Abspielen und Steuern von Soundeffekten von Objekten, zum Beispiel: |
   |
    |
   |
Vollziehen Sie die folgenden Schritte nach, um einzelne Anweisungen auszutesten:
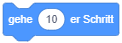
- Ziehen Sie den folgenden Block aus der Bibliothek auf die Arbeitsfläche:
- Wenn Sie einen Block in der Bibliothek oder auf der Arbeitsfläche anklicken, wird seine Aktion sofort ausgeführt: In diesem Fall wird das Objekt um 10 Einheiten entlang seiner (“Blick-")Richtung versetzt.
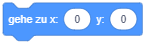
- Die x- und y-Koordinaten des ausgewählten Objekts und sein Richtungswinkel werden über der Objektliste angezeigt. Die Initialwerte sind (0, 0) und 90° (“schaut” nach rechts).
- Klicken Sie auf den Wert 10 im Block und geben Sie einen anderen Wert ein, um kleinere oder größere Schritte auszuführen (z. B. 5-er oder 20-er Schritte). Probieren Sie auch negative Werte aus.
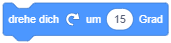
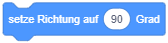
- Drehen Sie das Objekt mehrmals in 15°-Schritten im Uhrzeigersinn, indem Sie den folgenden Block auf die Arbeitsfläche ziehen und mehrmals anklicken:
- Wenn Sie anschließend den Block “gehe Schritt” anklicken, stellen Sie fest, dass sich das Objekt nun in eine andere Richtung bewegt, nämlich entlang seiner neuen (“Blick-")Richtung.
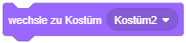
- Ziehen Sie einen weiteren Block aus der Kategorie “Aussehen” auf die Arbeitsfläche:
Dieser Block bewirkt, dass die Grafik des Objekts sich ändert: Es wird die nächste Grafik in der “Kostüm”-Liste der Figur ausgewählt. Welche Grafiken das Objekt momentan besitzt, sehen Sie, wenn Sie über den Reiter “Kostüm” in den Grafik-Arbeitsbereich wechseln. - Auf diese Weise können Sie weitere einzelne Anweisungen austesten, beispielsweise auch das Abspielen von Soundeffekten des Objekts:
- Wählen Sie nun einen Block und verschieben Sie ihn mit gedrückter Maustaste an den unteren Rand eines anderen Blocks, so dass sich die Blöcke verbinden. Wenn Sie nun auf den verbundenen Blockstapel klicken, werden Sie nacheinander ausgeführt.
- So können beliebig lange Anweisungsfolgen (Sequenzen) erstellt werden. Fügen Sie testhalber mehrere Blöcke zusammen, die eine kurze Animationssequenz umsetzen.
- Speichern Sie das Projekt nun als Datei auf Ihrem Rechner (z. B. als Erste_Schritte.sb3), indem Sie im “Datei”-Menü die Option “Auf deinen Computer herunterladen” wählen.
🎓 Projekt erkunden
Ein kleines Beispielprojekt Unterwasserwelt.sb3 zum eigenen Erkunden können Sie hier herunterladen: Download
- Öffnen Sie das Projekt es in Scratch, indem Sie im “Datei”-Menü die Option “Von deinem Computer hochladen” wählen.
- Starten Sie das Programm, indem Sie erst auf das Symbol
 oben rechts und anschließend auf das Symbol
oben rechts und anschließend auf das Symbol  klicken, und erkunden Sie es.
klicken, und erkunden Sie es. - Kehren Sie anschließend durch Klicken auf das Symbol
 zur Entwurfsmodus zurück. Versuchen Sie intuitiv anhand der Bausteine im Arbeitsbereich nachzuvollziehen, wie sich die Figuren verhalten und auf welche Eingaben sie reagieren.
zur Entwurfsmodus zurück. Versuchen Sie intuitiv anhand der Bausteine im Arbeitsbereich nachzuvollziehen, wie sich die Figuren verhalten und auf welche Eingaben sie reagieren. - Klicken Sie auf die Figurensymbole im Bereich unter der Bühne, um die Skripte der verschiedenen Figuren anzuzeigen. Auch die Bühne besitzt eigene Skripte.
- Falls Ihnen dabei Interaktionsmöglichkeiten auffallen, die Sie im laufenden Programm noch nicht entdeckt haben, starten Sie das Programm erneut und testen Sie diese.
Figuren und Bühne
Mit Hilfe der oben eingeführten Anweisungen kann das Verhalten und die Darstellung der Objekte gesteuert werden, also etwa ihre Position oder ihr Bild auf der Bühne.
Abstrakter gesprochen besitzt jedes Objekt verschiedene Attribute, also Eigenschaften, deren Werte sich durch ihre Skripte ändern lassen. Der Zustand eines Objekts zu einem bestimmten Zeitpunkt ist im Wesentlichen durch die Werte seiner Attribute definiert.
Daneben besitzt jedes Objekt einen Namen, durch den es identifiziert wird, eigene Skripte, durch die es gesteuert wird, sowie eigene Grafiken (“Kostüme”) und Soundeffekte, die in seinen Skripten verwendet werden können.
Attribute der Objekte
Objekte in Scratch haben größtenteils Attribute, die bestimmen, wie die Objekte auf der Bühne dargestellt werden. Die wichtigsten Attribute sind dabei:
- Die Position der Figur wird durch ihre x- und y-Koordinaten auf der Bühne beschrieben (-240 bis 240 für x, -180 bis 180 für y).
- Die Richtung der Figur wird durch einen Winkel in Grad beschrieben (-180° bis 180°).
- Das Attribut Kostüm-Nummer gibt an, welche ihrer Grafiken für die Figur momentan angezeigt wird.
- Das Attribut Größe der Figur legt die Skalierung ihrer Darstellung in Prozent fest (100 für normale Größe).
- Die Sichtbarkeit der Figur legt fest, ob die Figur auf der Bühne angezeigt wird oder nicht.
- Das Attribut Lautstärke der Figur legt in Prozent fest, wie laut die Soundeffekte der Figur abgespielt werden (100 für normale Lautstärke).
Die Bühne hat dagegen nur die Attribute Bühnenbild-Nummer (entspricht der Kostüm-Nummer der Figuren) und Lautstärke.
Eine Figur kann sichtbar oder unsichtbar sein. Unsichtbare Objekte werden nicht auf der Bühne angezeigt und sie können nicht angeklickt werden.
Daneben lassen sich noch über die “Effekt”-Blöcke aus der Kategorie “Aussehen” verschiedene Grafikeffekte für jede Figur und die Bühne einstellen, z. B. Transparenz, Helligkeit oder Farbverschiebung. Außerdem hat jede Figur einen Drehtyp, der festlegt, wie sich ihre Richtung auf die Darstellung auswirkt (siehe Koordinatensystem).
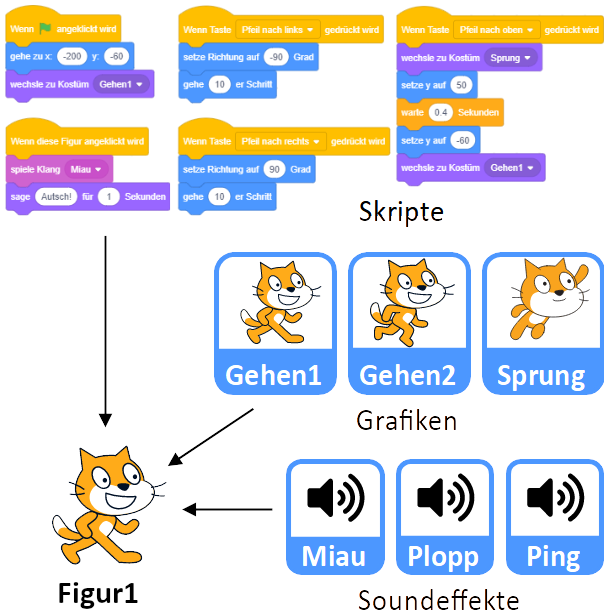
Die Werte der wichtigsten Attribute (Position, Richtung, Größe und Sichtbarkeit) werden im Attributfenster unterhalb der Bühne für die momentan ausgewählte Figur angezeigt und können dort auch im Entwurfsmodus manuell geändert werden.
Dort können Sie auch einen eindeutigen Namen für jedes Objekt festlegen. Über diesen Namen wird das Objekt in Skripten identifiziert, siehe z. B. die Auswahlmöglichkeiten im Block “gleite zu …”:
![]()
Koordinatensystem
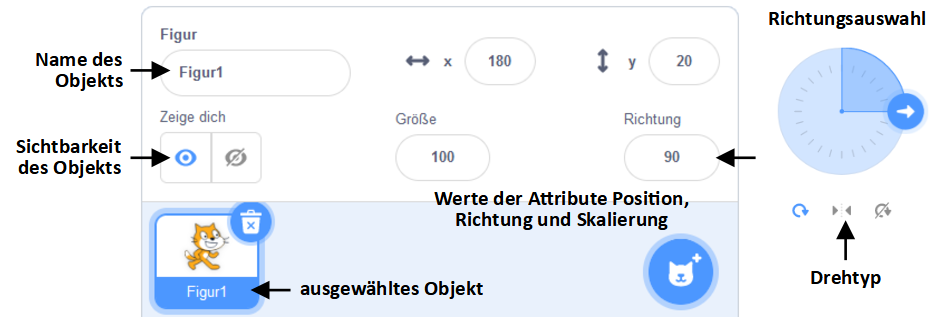
Alle Positionen auf der Bühne werden durch ihre x- und y-Koordinaten in einem kartesischen Koordinatensystem beschrieben. Der Punkt (0, 0) befindet sich dabei im Mittelpunkt. Die x-Koordinaten (horizontal) reichen von -240 (links) bis 240 (rechts), die y-Koordinaten von -180 (unten) bis 180 (oben). Richtungen werden im Uhrzeigersinn angegeben, wobei 0° den Richtungspfeil parallel zur y-Achse (nach oben) angibt. 90° entspricht also dem Richtungpfeil nach rechts, -90° nach links und 180° (bzw. -180°) nach unten.
Die Position eines Objekts bezieht sich immer auf ihren Drehpunkt (bei den in der Figurenbibliothek vorhandenen Objekten meistens der Mittelpunkt der Grafik). Um diesen Punkt dreht sich das Objekt auch, wenn seine Richtung geändert wird. Öffnen Sie das “Kostüm” eines Objekts im Arbeitsbereich, um zu sehen, wo sein Drehpunkt liegt.
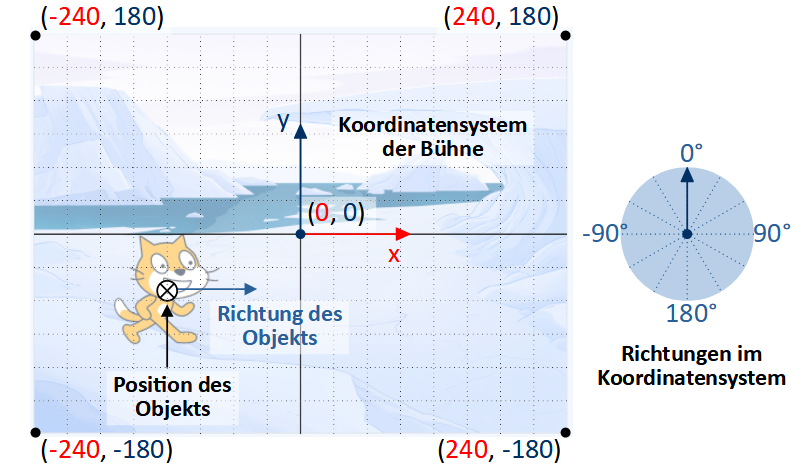
Die Grafik einer Figur wird üblicherweise um ihre Richtung gedreht dargestellt. Für jede Figur kann aber auch ein anderes Verhalten (ein anderer “Drehtyp”) festgelegt werden:
- Das Standardverhalten (Grafik drehen) stellt der Drehtyp “rundherum” dar. Diese Darstellung eignet sich besonders für Objekte in der Draufsicht.
- Der Drehtyp “links-rechts” spiegelt die Figur bei Richtungen < 0° und stellt Sie sonst normal dar, was sich beispielsweise für Figuren in der Seitenansicht eignet.
- Bei “nicht drehen” wird die Figur immer ungedreht dargestellt, unabhängig von ihrer momentanen Richtung.
- Der Drehtyp kann manuell im Attributfenster festgelegt werden (auf den Wert von “Richtung” klicken) oder über einen Anweisungsblock in einem Skript geändert werden:
Auch die Position des Mauszeigers wird in den Koordinaten der Bühne gemessen und kann mit bestimmten Blöcken benutzt werden, z. B. um eine Figur auf die Position des Mauszeigers zu setzen oder in Richtung des Mauszeigers zu drehen:

Grafiken
Jedes Objekt besitzt eine oder mehrere eigene Grafiken, die zur Darstellung des Objekts verwendet werden können. Bei Figuren werden diese Grafiken in Scratch “Kostüme” genannt, für die Bühne stellen sie die Hintergrundbilder dar. Mit den Anweisungsblöcken aus der Kategorie “Aussehen” kann in einem Skript die Grafik des Objekts, zu dem das Skript gehört, gewechselt werden. Wählen Sie den Reiter  “Kostüme”, um in den Grafik-Arbeitsbereich zu wechseln.
“Kostüme”, um in den Grafik-Arbeitsbereich zu wechseln.
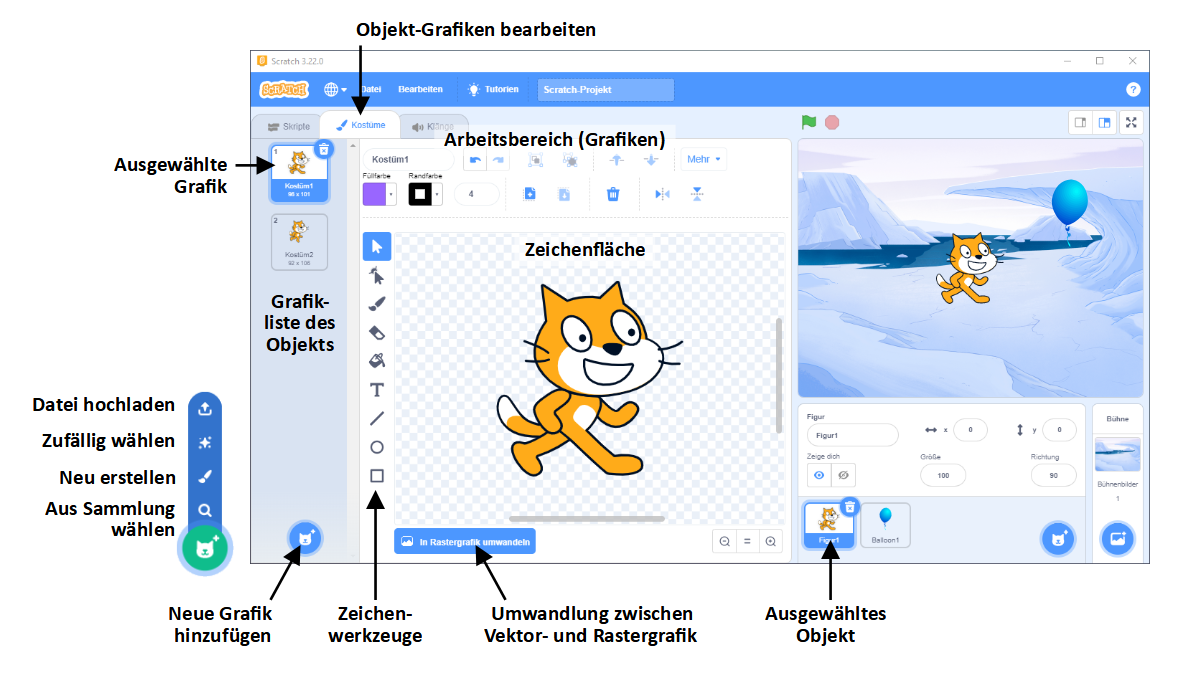
Hier sehen Sie links die Liste der Grafiken, die zur momentan ausgewählten Figur gehören (bzw. die Hintergrundbilder, die zur Bühne gehören). Klicken Sie auf eine Grafik, um Sie in der Zeichenfläche zu öffnen und zu bearbeiten. Je nachdem, ob es sich um eine Rastergrafik oder eine Vektorgrafik handelt, stehen verschiedene Werkzeuge zum Zeichnen zur Verfügung. Im Vektorgrafikmodus können Sie einfache geometrische Formen erstellen und nachträglich durch Verschieben einzelner Punkte verformen. Die Zeichenwerkzeuge ähneln denen bekannter Grafikprogramme wie Office Draw, Inkscape, GIMP oder Photoshop, sind aber deutlich reduzierter.
Über das Symbol ![]() bzw.
bzw.  unten links können Sie weitere Grafiken hinzufügen. Es erscheint eine Menüleiste, in der Sie auswählen können, ob Sie eine Grafik aus der Bildersammlung von Scratch wählen, eine neue Grafik auf der Zeichenfläche erstellen oder eine Bilddatei von Ihrem Rechner hochladen möchten. Scratch erkennt die gängigsten Bildformate BMP, PNG, JPEG und GIF (GIF-Animationen werden als Bildsequenzen importiert), sowie das Vektorgrafikformat SVG.
unten links können Sie weitere Grafiken hinzufügen. Es erscheint eine Menüleiste, in der Sie auswählen können, ob Sie eine Grafik aus der Bildersammlung von Scratch wählen, eine neue Grafik auf der Zeichenfläche erstellen oder eine Bilddatei von Ihrem Rechner hochladen möchten. Scratch erkennt die gängigsten Bildformate BMP, PNG, JPEG und GIF (GIF-Animationen werden als Bildsequenzen importiert), sowie das Vektorgrafikformat SVG.
Da die Werkzeuge zur Bildbearbeitung in Scratch eher rudimentär sind, kann es hilfreich sein, Grafiken mit einem komfortableren Tool zu erstellen (z. B. GIMP, Inkscape) oder aus einer Online-Sammlung herunterzuladen und in Scratch zu importieren. Umgekehrt können auch Bilder aus Scratch heraus in gängigen Formaten exportiert werden (PNG, SVG).
Soundeffekte
Neben Grafiken kann jedes Objekt auch seine eigenen Soundeffekte besitzen, die in seinen Skripten mit Anweisungsblöcken aus der Kategorie “Klang” abgespielt werden können. Wählen Sie den Reiter  “Klänge”, um zum Sound-Arbeitsbereich zu wechseln.
“Klänge”, um zum Sound-Arbeitsbereich zu wechseln.
Ähnlich wie im Grafik-Arbeitsbereich sehen Sie links die Liste der Soundeffekte, die zur momentan ausgewählten Figur oder der Bühne gehören. Wählen Sie einen Soundeffekt per Mausklick aus, um ihn zu bearbeiten. Dazu stehen einfache Werkzeuge wie Beschneiden, Ändern der Geschwindigkeit, Lautstärke und Ein-/Ausblenden zur Verfügung.
Über das Symbol  unten links können Sie weitere Soundeffekte hinzufügen (aus der Soundsammlung von Scratch auswählen, eine Audiodatei von Ihrem Rechner hochladen oder mit dem Mikrofon aufnehmen).
unten links können Sie weitere Soundeffekte hinzufügen (aus der Soundsammlung von Scratch auswählen, eine Audiodatei von Ihrem Rechner hochladen oder mit dem Mikrofon aufnehmen).
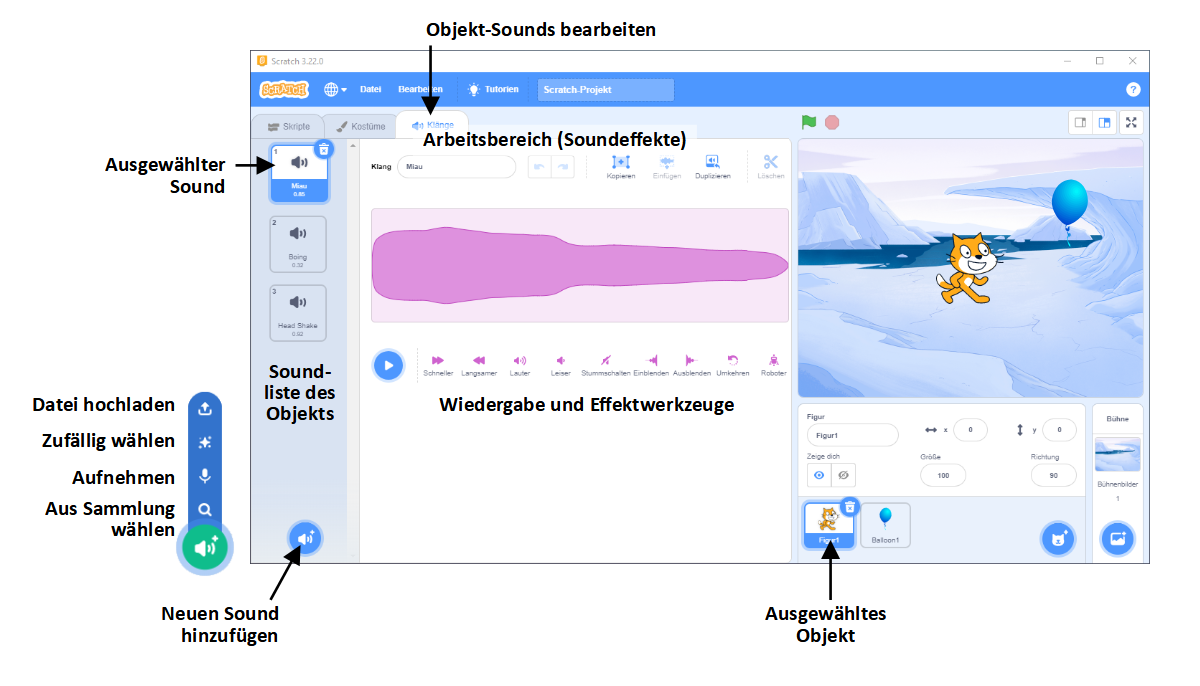
Da Soundeffekte auf Dauer störend sein können, ist es empfehlenswert, sie nur sparsam bzw. möglichst nur mit vorhandenen Kopfhörern einzusetzen.
🎓 Übung
- Öffnen Sie Ihr Scratch-Projekt aus Erste Schritte und benennen Sie das Objekt, das momentan “Figur1” heißt, sinnvoller um (z. B. “Scratch”).
- Der Bühnenhintergrund ist momentan noch leer. Fügen Sie ein Szenenbild zur Bühne hinzu und wählen Sie ein Bild aus der Sammlung aus. Das leere Bühnenbild kann gelöscht werden.
- Fügen Sie der Figur eine neue Grafik für eine Sprunganimation hinzu. Wählen Sie aus der Bildersammlung “Cat Flying-b” (benennen Sie die Grafiken in der Grafikliste des Objekts ggf. um, z. B. “Sprung”).
- Nun soll als weiteres Objekt ein Ballon hinzugefügt werden. Wählen Sie ein passendes Objekt aus der Figurensammlung von Scratch und positionieren Sie den Ballon auf der Bühne.
- Als Nächstes soll dem Ballon ein Gesicht verpasst werden. Öffnen Sie dazu die Grafik des Ballons im Zeichenbereich und bearbeiten Sie sie. Alternativ können Sie auch das Gesicht der Katze kopieren (im Zeichenbereich öffnen, Elemente auswählen und mit
 kopieren) und in die Grafik des Ballons einfügen.
kopieren) und in die Grafik des Ballons einfügen.
Skripte und Ereignisse
Anweisungen und Sequenzen
Anweisungen sind – wie wir bereits kennengelernt haben – elementare, eindeutige Befehle, mit denen sich beispielsweise Objekte steuern lassen. Blöcke, die eine Anweisung repräsentieren (also z. B. “bewege dich”, “ändere deine Grafik”), haben in Scratch die Form eines Puzzleteils, an das oben und unten angelegt werden kann (“Stapelblockform”):
Diese Blöcke können durch vertikales Aneinanderhängen zu Sequenzen verbunden (“gestapelt”) werden. Solche Blockstapel werden immer im Verbund von oben nach unten Anweisung für Anweisung (sequenziell) ausgeführt. Sequenzen stellen die einfachste Form von Programmen dar.
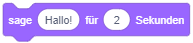
Beachten Sie, dass einige Anweisungen eine bestimmte Dauer zur Ausführung benötigen und während dieser Zeit der Ablauf der Sequenz pausiert wird. Vergleichen Sie dazu, wie sich der Ablauf ändert, wenn Sie an den Beginn einer Sequenz einmal den Block “sage …” und einmal den Block “sage … für … Sekunden” setzen:
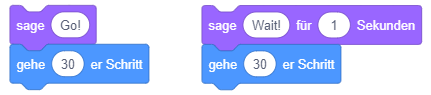
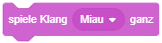
Dasselbe gilt beispielsweise auch für Anweisungen wie “gleite” (eine kontinuierliche Bewegung über einen bestimmten Zeitraum), “spiele Klang ganz” (wartet bis der Soundeffekt zuende abgespielt wurde) oder die einfache “warte”-Anweisung aus der Kategorie “Steuerung”:


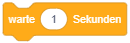
Parameter und Werte
Bei den bisher vorgestellten Anweisungen hängt das Verhalten meistens von einem oder mehreren Werten ab, die in die ovalen Eingabefelder des Blocks eingetragen werden, z. B. um wie viel Grad ein Objekt bei einem “drehe dich”-Block gedreht werden soll oder was für wie viele Sekunden bei einem “sage”-Block angezeigt werden soll. Solche Werte werden im Allgemeinen als Parameterwerte (oder auch Argumente) der Anweisung bezeichnet. In Scratch können Parameterwerte direkt eingetragen werden oder aus speziellen Blöcken, den “Werteblöcken” abgefragt werden.

Ein Werteblock wird in Scratch durch einen ovalen Block dargestellt:
Werteblöcke können für alle Parameter von Anweisungen verwendet werden, indem sie in den entsprechenden ovalen Eingabefeldern des Anweisungsblocks platziert werden. Wird der Anweisungsblock ausgeführt, so wird zunächst der aktuelle Wert des Werteblocks abgefragt und für den entsprechenden Parameter der Anweisung verwendet. Sie können den aktuellen Wert eines Werteblocks im Entwurfsmodus auch jederzeit manuell überprüfen, indem Sie ihn in der Block-Bibliothek einfach anklicken.
Das folgende Beispiel lässt ein Objekt seinen aktuellen Richtungswinkel in einer Sprechblase anzeigen:
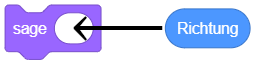

Für jedes Attribut eines Objekts gibt es einen speziellen Werteblock in der entsprechenden Kategorie, z. B. Werteblöcke für die x- und y-Koordinate und den Richtungswinkel in der Kategorie “Bewegung”:



Daneben gibt es einen speziellen Block in der Kategorie “Fühlen” (türkis), über den jedes Attribut eines beliebigen Objekts oder der Bühne abgefragt werden kann. Über die beiden Auswahllisten ▾ wird das gewünschte Objekt und Attribut ausgewählt, hier beispielsweise die Nummer des momentan ausgewählten Hintergrundbilds der Bühne oder die y-Koordinate des Objekts “Figur1”:


Neben Werteblöcken zum Abfragen von Objekt-Attributen gibt es weitere Blöcke, die globale Werte messen, etwa die Position des Mauszeigers, die Lautstärke, die das Mikrofon gerade misst, oder die Anzahl an Sekunden, die von der in Scratch integrierten Stoppuhr bisher gezählt wurden. Auch diese Blöcke befinden sich in der Kategorie “Fühlen”:




 Die Werte der wichtigsten Attribute können auch live auf der Bühne angezeigt werden. Suchen Sie dazu den entsprechenden Werteblock der Form
Die Werte der wichtigsten Attribute können auch live auf der Bühne angezeigt werden. Suchen Sie dazu den entsprechenden Werteblock der Form 
Dadurch können Sie während der Programmausführung überprüfen, welche Werte die Attribute zu jedem Zeitpunkt haben und in welchen Situationen sich die Werte ändern. Diese Information kann hilfreich sein, um das Programmverhalten nachzuvollziehen und durch Abweichungen vom erwarteten Verhalten Fehler zu finden.
Ereignisse
Bisher haben wir Anweisungen direkt in der Arbeitsfläche oder in der Block-Bibliothek durch Anklicken ausgeführt, um ihr Verhalten zu untersuchen. Dieses Ausprobieren ist nur im Entwurfsmodus möglich. Um ein “echtes” Programm zu erstellen (das im Präsentationsmodus vernünftig genutzt werden kann), muss festgelegt werden, durch welches Ereignis ein Skript automatisch ausgelöst werden soll.
Wie oben erwähnt, werden Programme in Scratch üblicherweise durch Anklicken der grünen Fahne gestartet. Um festzulegen, dass ein Skript durch dieses Ereignis automatisch ausgeführt wird, wählen Sie die Kategorie “Ereignisse” in der Block-Bibliothek und ziehen Sie den Block “Wenn  angeklickt wird” in den Arbeitsbereich:
angeklickt wird” in den Arbeitsbereich:

Hängen Sie nun mehrere Anweisungsblöcke an diesen Blöck an und beobachten Sie, was passiert, wenn Sie die grüne Fahne anklicken: Die Anweisungssequenz wird ausgeführt (auch im Präsentationsmodus).
Um Skripte für verschiedene Ergebnisse (beispielsweise Eingaben über Tastatur oder Maus) zu definieren, stellt Scratch neben dem “Startereignis”-Block noch weitere Blöcke bereit. Solche Ereignisblöcke stehen immer am Anfang eines Skripts und haben in Scratch die Form eines Puzzleteils, das oben gewölbt ist (“Kopfblockform”):
Sobald das entsprechende Ereignis eintritt, wird die Anweisungssequenz, die an den Ereignisblock angehängt ist, sofort abgearbeitet – unabhängig davon, in welchem Zustand sich das Programm gerade befindet. Dabei können sogar beliebig viele Skripte zur gleichen Zeit ausgeführt werden, also parallel nebeneinander laufen! Im Folgenden werden die wichtigsten Ereignisblöcke beschrieben, mit denen sich interaktive Anwendungen umsetzen lassen.
Verhalten beim Programmstart
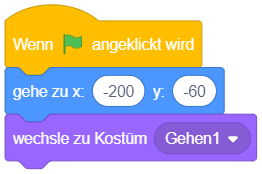
Das angehängte Skript wird ausgeführt, wenn auf die grüne Fahne  geklickt wird.
Das Anklicken der grünen Fahne wird üblicherweise für den Programm- bzw. Spielstart genutzt.
geklickt wird.
Das Anklicken der grünen Fahne wird üblicherweise für den Programm- bzw. Spielstart genutzt.
Dieses Ereignis wird oft verwendet, um die Objekte und die Welt als Erstes zu initialisieren, also in einen gewünschten Anfangszustand zu bringen. Beispielsweise kann für jedes Objekt auf der Bühne ein Skript für das Startereignis festgelegt werden, das es auf seine Startposition setzt, seine initiale Grafik, Richtung und Sichtbarkeit festlegt. Wenn das Objekt zu Beginn noch nicht gleich sichtbar sein soll, kann das durch einen “verstecke dich”-Block im Startskript erreicht werden.
Anschließend können weitere Anweisungen folgen, die dafür sorgen, dass das Objekt beim Programmstart sofort anfängt, etwas zu machen – beispielsweise einen Begrüßungstext anzeigen, Hintergrundmusik abspielen oder eine Animationssequenz starten: Das folgende Skript sorgt beispielsweise beim Programmstart dafür, dass das Hintergrundbild “Titelbild” angezeigt wird und eine Titelmelodie abgespielt wird:
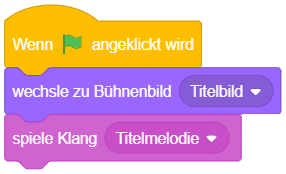
Reaktion auf Tastatureingabe
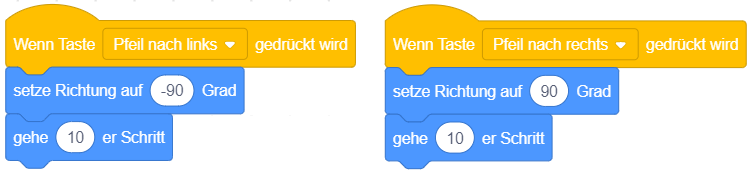
Das angehängte Skript wird immer dann ausgeführt, sobald eine bestimmte Taste auf der Tastatur gedrückt wird. Die Taste kann über die Auswahlliste ▾ festgelegt werden.
Dieses Ereignis kann zum Beispiel verwendet werden, um eine Figur mit den Pfeiltasten der Tastatur auf der Bühne zu bewegen. Das oben stehende Beispiel bewirkt, dass die Figur bei jedem Drücken der Pfeiltasten nach links oder rechts gedreht und um 10 Einheiten entlang seiner Blickrichtung bewegt wird.
Das folgende Beispiel lässt die Figur beim Drücken der Pfeiltaste kurz nach oben “springen”, wobei eine andere Grafik angezeigt wird, welche die Figur springend zeigt:
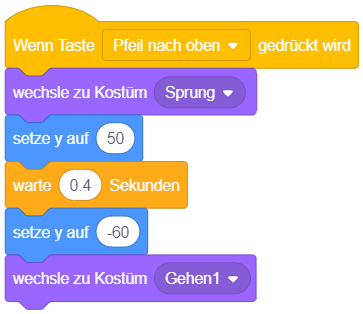
Im Gegensatz zum ersten Beispiel benötigt dieses Skript eine bestimmte Zeit, bis es zuende ausgeführt wird, da eine “warte”-Anweisung verwendet wird (in diesem Fall 0.4 Sekunden).
Reaktion auf Mausklick
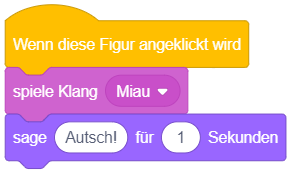
Das angehängte Skript wird immer dann ausgeführt, sobald mit der Maus auf die Figur geklickt wird, zu der das Skript gehört. Ist das Skript für die Bühne definiert, wird es durch jeden Mausklick in die Bühnenfläche gestartet. Es spielt dabei keine Rolle, welche Maustaste gedrückt wird.
Das Ereignis lässt sich wie das vorige verwenden, um Interaktionsmöglichkeiten zwischen Menschen und dem Programm zu realisieren. Im oben stehenden Beispiel wird als Reaktion auf das Anklicken der Figur, zu der das Skript gehört, ein Soundeffekt abgespielt und eine Mitteilung in Form einer Sprechblase angezeigt.
Verhalten beim Szenenwechsel

Das angehängte Skript wird ausgeführt, sobald das Hintergrundbild der Bühne zu dem angegebenen Bild wechselt. Das Bild kann über die Auswahlliste ▾ festgelegt werden.
Durch verschiedene Bühnenbilder werden oft verschiedene Abschnitte des Programms repräsentiert. Dadurch lassen sich insbesondere umfangreichere Programme besser strukturieren. In einem Animationsfilm können das beispielsweise verschiedene Szenen oder in einem Spiel verschiedene Spielabschnitte (“Level”) sein, sowie Titelbild und Spielende (“Game Over”) oder Abspann.
Dafür ist es hilfreich, bei jedem Wechsel zu einem neuen Abschnitt die Objekte geeignet zu (re-)initialisieren, ähnlich wie beim Programmstart. Auf einem Titelbild oder “Game Over”-Bildschirm sollten die Spielfiguren in der Regel nicht sichtbar sein, während Sie beim Wechsel zu einem Spielabschnitt auf ihre entsprechenden Startpositionen gesetzt werden müssen.
Das oben dargestellte Beispiel lässt ein Objekt beim Wechsel zur zweiten Szene “von der Bühne abtreten”, während es beim Wechsel zurück zur ersten Szene wieder sichtbar wird.

Zur Umsetzung interaktiver Anwendungen mit Scratch bietet es sich an, von den Ereignissen bzw. Eingaben aus zu denken, also: “Was soll passieren, sobald …?” bzw. “Wie soll Objekt X reagieren, sobald …?”. Eine komplexere Aufgabe wird also gedanklich ereignisbasiert in kleinere Teilaufgaben zerlegt.
Die “Start”- und “Szenenwechsel”-Ereignisse können verwendet werden, um den gewünschten Initialzustand der Objekte und der Welt herzustellen und gegebenenfalls einen automatischen Ablauf für die Szene zu starten. Mit den Ereignissen “Figur angeklickt” und “Taste gedrückt” kann dagegen auf Eingaben reagiert werden.
🎓 Übung
- Öffnen Sie Ihr Scratch-Projekt aus Erste Schritte und fügen Sie die oben dargestellten Skripte zur Figur “Scratch” hinzu. Alternativ können Sie das Projekt Erste_Schritte.sb3 auch hier herunterladen: Download
- Passen Sie die beiden Skripte zum Gehen nach links/rechts so an, dass bei jedem Schritt eine Animationsequenz der Form “gehe Schritt”, “wechsle zu Kostüm 2”, “warte”, “gehe Schritt”, “wechsle zu Kostüm 1”, “warte” abgespielt wird.
- Die Sprunganimation der Figur “Scratch” ist momentan etwas ruckartig. Ersetzen Sie die Anweisungen “setze y auf” und “warte” durch die Anweisung “gleite zu Position”, um eine kontinuierliche Auf- und Abwärtsbewegung umzusetzen.
- Fügen Sie der Figur “Ballon” ein Skript hinzu, das ihn beim Anklicken zu einer zufälligen Position gleiten lässt.
- Prüfen Sie, ob der Zustand der Figuren bei jedem Programmstart immer gleich ist. Überprüfen Sie dazu, welche Attribute der Figuren durch Eingaben geändert werden können. Korrigieren Sie die Skripte zum Initialisieren der Figuren, falls nötig.
- Erweitern Sie das Projekt nun um ein Bühnenbild, das ein Titelbild darstellt. Zwischen Titelbild und Szenenbild soll beim Drücken der Leertaste gewechselt werden. Beim Programmstart soll die Bühne immer das Titelbild darstellen.
- Passen Sie das Projekt nun so an, dass alle Figuren nur auf dem Szenenbild sichtbar sind, aber nicht auf dem Titelbild. Verwenden Sie dazu den Ereignisblock “Wenn das Bühnenbild wechselt”.
Parallele Skriptabläufe
Wie oben erwähnt können in Scratch quasi beliebig viele Skripte verschiedener Objekte oder auch desselben Objekts quasi gleichzeitig ausgeführt werden. Das spielt insbesondere bei Skripten, die eine gewisse Ausführungsdauer haben, eine Rolle.
Zur Veranschaulichung betrachten wir noch einmal das “Sprung”-Beispiel von oben:

Dieses Skript benötigt 0.4 Sekunden zur Ausführung, da es eine “warte”-Anweisung enthält. Während das Skript läuft, können aber andere Skripte des Objekts zeitlich parallel zu diesem Skript ausgeführt werden. Wird etwa kurz nach der Pfeiltaste nach oben die Pfeiltaste nach rechts bewegt, bewegt sich die Figur in der Luft einen Schritt nach rechts, bevor sie wieder auf den Boden fällt.
Um parallele Skriptabläufe examplarisch zu untersuchen, können diese grafisch in Form eines Balkendiagramms über eine Zeitachse aufgetragen werden. Die Länge der Balken entspricht dabei der Dauer der Skriptabläufe, ihre Startpositionen sind durch eine vorgegebene Beispielsequenz von Ereignissen bzw. Eingaben gegeben:
Parallele Skriptabläufe können problematisch sein, wenn verschiedene Skripte dieselben Attribute eines Objekts ändern und sich damit gegenseitig in die Quere kommen. Diese Problematik sollte bei der ereignisorientierten Programmentwicklung im Hinterkopf behalten werden.
Scratch-Erweiterungen
Für Scratch sind verschiedene ergänzende Block-Kategorien vorhanden, die zu Beginn nicht sichtbar sind, und Scratch um Multimedia-Funktionen, Kommunikation mit externer Hardware und Online-Diensten erweitert. Die Erweiterungen lassen sich über das Symbol  unten links auswählen.
unten links auswählen.
Viele dieser Erweiterungen stellen größtenteils neue Anweisungs- und Werteblöcke bereit, deren Verhalten sich durch Ausprobieren und Intuition schnell erschließt. Für den Einstieg eignen sich hier besonders die folgenden Erweiterungen:
 |
Die Erweiterung “Malstift” stellt Anweisungen zum Zeichnen auf der Bühne bereit. Figuren können damit als Zeichenstifte fungieren, ähnlich den sogenannten Turtle-Grafiken: Wenn die Anweisung “schalte Stift ein” ausgeführt wird, hinterlässt die Figur eine Zeichenspur während sie sich über die Bühne bewegt, bis der Stift wieder abgeschaltet wird. Über weitere Anweisungen kann die Stiftfarbe und -dicke zum Zeichnen gewählt werden. |
 |
Die Erweiterung “Musik” enthält Anweisungen zum Abspielen verschiedener Instrumente und Schlaginstrumente und eignet sich besser zum Musizieren als die “Klang”-Anweisungen. |
 |
Die Erweiterung “Text zu Sprache” stellt Anweisungen bereit, um Texte mit verschiedenen Stimmen vorlesen zu lassen, statt sie über Sprechblasen anzuzeigen. Diese Erweiterung basiert auf Amazon Web Services und benötigt eine laufende Internetverbindung. |
 |
Die Erweiterung “Übersetzen” stellt einen Werteblock zum Übersetzen von Wörtern in verschiedene Sprachen zur Verfügung. Auch diese Erweiterung basiert auf Amazon Web Services. |
Fachkonzepte
In diesem Einstieg in die visuelle Programmierung mit Scratch haben wir bereits eine ganze Reihe von Programmierkonzepten kennengelernt, die von modernen Programmiersprachen unterstützt werden. Im Folgenden werden diese Konzepte und ihre Fachbegriffe kurz rekapituliert.
Imperative Programmierung
Als imperative Programmierung wird in der Informatik das Konzept bezeichnet, nach dem ein Programm aus einer klar definierten Abfolge von Handlungsanweisungen besteht. Im einfachsten Fall listet ein Programm Anweisungen auf, die in der angegebenen Reihenfolge nacheinander vom Computer abgearbeitet werden. Eine solche lineare Aneinanderreihung von Anweisungen wird als Sequenz bezeichnet, zum Beispiel:
Eine Anweisung (auch Befehl, Kommando oder Instruktion genannt) stellt eine einzelne Handlungsvorschrift dar, die je nach Programmiersprache oder programmiertem System unterschiedlich sein kann. Dazu gehören unter anderem das Ändern der Attributwerte von Objekten (in Scratch zum Beispiel das Ändern der Position einer Figur oder Wechsel zum nächsten Kostüm) oder visuelle und akustische Ausgaben (in Scratch zum Beispiel die Anzeige einer Sprechblase oder das Abspielen eines Soundeffekts). Anweisungen können über Parameter weitere Informationen zu ihrer Ausführung übergeben bekommen.
Um die Abfolge der Anweisungen zu steuern, also beispielweise Anweisungen wiederholt oder in Abhängigkeit von bestimmten Bedingungen auszuführen, werden in der imperativen Programmierung sogenannte Kontrollstrukturen verwendet, die wir in der nächsten Lektion kennenlernen werden.
Ereignisorientierte Programmierung
Das Konzept zu programmieren, indem für bestimmte Ereignisse festgelegt wird, welche Anweisungen beim Eintreten des Ereignisses ausgeführt werden sollen, wird in der Informatik als ereignisorientierte Programmierung bezeichnet. Dieses Programmierkonzept eignet sich besonders gut, um interaktive Systeme zu programmieren, also solche, in denen das System auf Eingaben oder Ereignisse reagieren muss, die zu beliebigen Zeitpunkten auftreten können (asynchrone Ereignisse).
Besonders in der Entwicklung von grafischen Benutzeroberflächen (GUIs) und Webanwendungen hat sich dieses Konzept bewährt. Hier stellen die Ereignisse meist Aktionen von Menschen dar, die mit der GUI interagieren, beispielsweise durch eine Eingabe in ein Textfeld oder einen Mausklick auf eine Schaltfläche.
Scratch kombiniert also, soweit wir bisher gesehen haben, die Konzepte der imperativen Programmierung und der ereignisorientierten Programmierung: Jedes einzelne Skript besteht aus einer Folge von Anweisungen, die nacheinander abgearbeitet werden. Ein Skript startet dabei immer dann, sobald das als Einstiegspunkt für das Skript festgelegte Ereignis eintritt (repräsentiert durch den gelben Ereignis-Block am Kopf eines Skripts).
Nebenläufigkeit
Insbesondere für die ereignisorientierte Programmierung ist entscheidend, dass das System, auf dem das Programm ausgeführt wird, in der Lage ist, mehrere Programmteile quasi gleichzeitig, also zeitlich parallel abarbeiten zu können, damit es nicht zu Verzögerungen kommt, wenn mehrere Ereignisse auf einmal eintreten, auf die reagiert werden muss. Dieses Konzept wird in der Informatik als Nebenläufigkeit bezeichnet.
Scratch unterstützt parallele Programmausführung: Skripte verschiedener Objekte, die auf dasselbe Ereignis reagieren, werden (scheinbar) gleichzeitig ausgeführt.
Objekte, Attribute und Methoden
Die Figuren und die Bühne in Scratch stellen Objekte im Sinne der Programmierung dar. Sie haben eine Identität, einen Zustand und ein Verhalten. Der Zustand eines Objekts ist durch die Werte seiner Attribute definiert (z. B. Position, Größe). Das Verhalten der Objekte ist durch ihre Skripte definiert. Skripte sind hier also (Teil-)Programme, die zu jeweils einem Objekt gehören. Solche (Teil-)Programme werden auch als Methoden des Objekts bezeichnet.
1.2.1 Übungsaufgaben
Stoffwiederholung
Aufgabe 1: Anweisungen erläutern
Beantworten Sie die folgenden Fragen zu den dargestellten Anweisungen, die jeweils zum Skript des Objekts “Figur1” gehören.
Testen Sie die Anweisungen in Scratch aus, wenn Sie sich nicht sicher sind.
| Anweisung/Sequenz | |
|---|---|
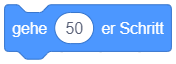 |
Welche Attribute werden geändert? Von welchen weiteren Attributen hängt der Effekt ab? Zusatzfrage: Welchen Effekt hätte diese Anweisung, wenn ein negativer Parameterwert (z. B. -50) angegeben wird? |
 |
Welchen Effekt hat diese Anweisung? |
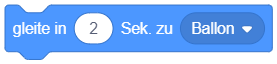 |
“Ballon” ist hier ein anderes Objekt auf der Bühne. Welches Objekt bewegt sich hier? Wovon hängt die Bewegungsgeschwindigkeit des Objekts ab? |
 |
Für welche Attribute ändern sich hier die Werte? |
 |
Welchen Effekt hat diese Anweisung, wenn gerade das letzte Kostüm der Figur ausgewählt ist? Was passiert, wenn die Figur nur ein Kostüm hat? |
 |
Angenommen, die Grafik der Figur ist 80 mal 80 Pixel groß. Welche Größe hat sie nach Ausführung dieser Sequenz? |
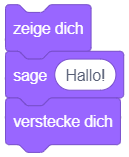 |
Welchen Effekt hat diese Sequenz? |
Aufgabe 2: Skripte vergleichen
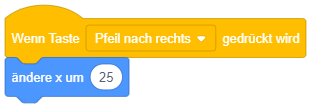
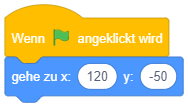
Vergleichen Sie jeweils das linke und das rechte Skript miteinander und ermitteln Sie jeweils, worin sich die Programmausführung in beiden Versionen unterscheidet. Beantworten Sie dazu die folgenden Fragen.
| Skript Version 1 | Skript Version 2 | |
|---|---|---|
 |
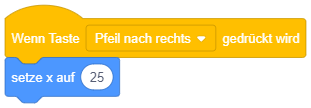 |
Angenommen, die Figur befindet sich momentan an Position (100, 100). An welcher Position befindet sie sich jeweils, nachdem die Pfeiltaste gedrückt wurde? |
 |
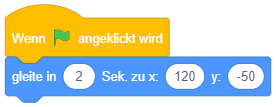 |
Angenommen, die Figur befindet sich vor dem Programmstart an Position (0, 0). An welcher Position befindet sie sich jeweils 1 Sekunde nach Programmstart? |
 |
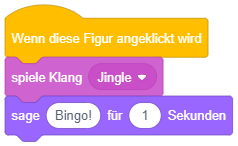 |
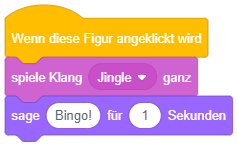
Angenommen, der Sound “Jingle” dauert 5 Sekunden. In welchem Zeitraum nach Anklicken der Figur wird der Sound jeweils gespielt, in welchem Zeitraum wird die Mitteilung angezeigt? |
 |
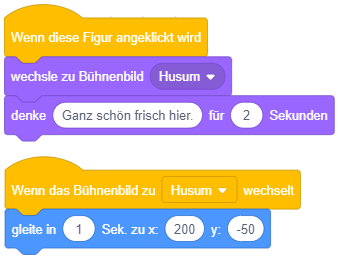 |
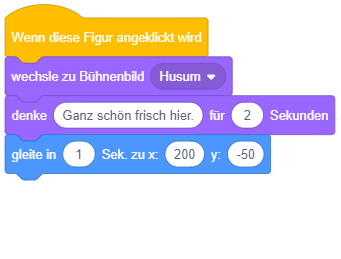
In welchem Zeitraum nach Anklicken der Figur bewegt sie sich jeweils, in welchem Zeitraum wird die Mitteilung angezeigt? |
Aufgabe 3: Programmablauf untersuchen
In dieser Aufgabe soll der zeitliche Ablauf von Skripten eines Programms bei bestimmten Eingaben nachvollzogen und grafisch dargestellt werden.
Laden Sie dazu die Projektdatei Unterwasserwelt.sb3 aus der Einführung herunter und öffnen Sie das Projekt in Scratch: Download
Das folgende Diagramm zeigt eine vertikale Zeitachse, in der die Zeitpunkte markiert sind, zu denen bestimmte Eingaben auftreten ( Download als PDF).
Ablauf skizzieren
Markieren Sie die Zeiträume, in denen Skripte ausgeführt werden, durch Balken in den Spalten der betreffenden Objekte. Beachten Sie dabei, dass ggf. auch mehrere Skripte eines Objekts gleichzeitig ausgeführt werden können. Kennzeichnen Sie dabei jedes Skript durch einen separaten Balken im Zeitdiagramm. Die zeitlichen Abläufe von Skripten der Figur “Fisch3” sind hier zur Orientierung bereits eingezeichnet.
Ablauf analysieren
Starten Sie das Programm und klicken Sie die Figur “Fisch2” wiederholt in schneller Folge an. Erklären Sie das beobachtete Programmverhalten. Welcher Sonderfall lässt sich daraus über die Ausführung von Skripten in Scratch ableiten?
Praktische Übungen
Animationssequenzen
Als erster Einstieg in Scratch werden oft kurze Filme, Dialoge oder Animationen erstellt, die zunächst größtenteils ohne Interaktion und mit rein sequenziellen Abläufen auskommen. So können sich die Schülerinnen und Schüler mit der Entwicklungsumgebung in kreativer Weise vertraut machen und die grundlegende Steuerung der Figuren, die Konzepte der Anweisungssequenzen und Ereignisse (Start und Szenenwechsel), sowie das Timing von Abläufen mittels Warteanweisungen und Ereignissen kennenlernen.
Als Vorlage für die Erstellung eines solchen Projekts kann zunächst ein Drehbuch (“Storyboard”) für den Ablauf entworfen werden, in dem die Aktionen aller Objekte in einer Bildsequenz (siehe Aufgabe Animationssequenz nach Drehbuch erstellen), tabellarisch oder über einer Zeitachse dargestellt werden. Der Ablauf lässt sich mit Hilfe verschiedener Bühnenbilder in einzelne Abschnitte aufteilen, die jeweils separat geplant werden können.
Ideen zu solchen Projekten finden sich beispielsweise in den offiziellen Scratch-Tutorials (siehe Projekte “Stell dir eine Welt vor” und “Erzähl eine Geschichte”) oder in der Broschüre “Scratch Projektideen” der Pädagogischen Hochschule Schwyz (siehe Projektidee “Ritter, Löwen und Prinzessinnen”).
Aufgabe 4: Animationssequenz nach Drehbuch erstellen
In dieser Aufgabe soll nach einem vorgegebenen Drehbuch eine kurze Animationssequenz – passend zum Thema “Anweisungen und Sequenzen” – mit mehreren automatisch agierenden Objekten in Scratch umgesetzt werden.
Laden Sie dazu die Projektdatei Drehbuch.sb3 als Vorlage herunter: Download
Das Projekt enthält vier Figuren (die Sprecherin “Luca”, zwei “Anweisungsblöcke” und ein “Fisch”-Objekt) und zwei Bühnenhintergründe (Titelbild und Hintergrund der Lektion). Die Animationssequenz soll beim Starten des Programms über das Symbol  nach dem folgenden Drehbuch ablaufen:
nach dem folgenden Drehbuch ablaufen:
 |
Kurz nach dem Programmstart mit  sagt Luca zuerst: “Als Erstes wird der Fisch mit einem einzelnen Block bewegt.” (Text A) sagt Luca zuerst: “Als Erstes wird der Fisch mit einem einzelnen Block bewegt.” (Text A) Während Luca spricht, soll sie immer mit der Grafik “Sprechen” angezeigt werden, sonst mit der Grafik “Warten”. |
 |
Anschließend gleitet der “gehe”-Block nach rechts in den Skriptbereich (1.) und dort erscheint kurz die Meldung “Klick!” (2.) Beim “Klick!” bewegt sich der Fisch ein Stück nach rechts. (3.) |
 |
Als Nächstes sagt Luca: “Nun hängen wir einen weiteren Block daran.” (Text B) |
 |
Nun gleitet der “drehe”-Block ebenfalls nach rechts zur Unterseite des “gehe”-Blocks (1.) und dort erscheint wieder kurz “Klick!” (2.) Beim “Klick!” bewegt sich der Fisch ein Stück nach rechts (3.) und dreht sich um 90°. (4.) |
 |
Als Letztes sagt Luca noch: “Hier wurden beide Anweisungen nacheinander ausgeführt.” (Text C) |
 |
Zusatzaufgabe: Beim Programmstart soll zuerst 2 Sekunden lang das Titelbild angezeigt werden, bevor zum Hintergrund der Lektion gewechselt wird und die Animationssequenz wie oben beschrieben beginnt. Die Figuren sollen auf dem Titelbild nicht sichtbar sein. |
Beachten Sie, dass die Animationssequenz auch mehrmals nacheinander durch Klicken auf  richtig abgespielt werden soll. Initialisieren Sie die Attribute der Objekte, die sich während der Programmausführung ändern, beim Start bzw. Szenenwechsel also geeignet.
richtig abgespielt werden soll. Initialisieren Sie die Attribute der Objekte, die sich während der Programmausführung ändern, beim Start bzw. Szenenwechsel also geeignet.
Das Projekt enthält in den Skriptbereichen der Figuren und der Bühne bereits alle Blöcke, die Sie zur Umsetzung des Drehbuchs benötigen (ggf. müssen aber noch Blöcke kopiert oder fehlende Parameterwerte eingetragen werden). Der “warte”-Block kann dabei verwendet werden, um das richtige Timing der Aktionen für die verschiedenen Objekte abzustimmen.










Zur Planung des zeitlichen Ablaufs kann es hilfreich sein, die Aktionen der Objekte in einem Zeitdiagramm zu skizzieren ( Download als PDF):
Interaktive Programme
Aufgabe 5: 2D-Transformation
In dieser Aufgabe sollen Interaktionen zum Bewegen, Drehen und Skalieren eines Objekts verwendet werden.
Laden Sie dazu die Projektdatei 2D-Transformation.sb3 als Vorlage herunter: Download
Auf dem Koordinatengitter befinden sich eine grüne und eine rote geometrische Figur. Die grüne Figur wird beim Programmstart zufällig positioniert, gedreht und skaliert (siehe Skript der Figur “Ziel”). Ziel des Spiels ist es, die rote Figur durch Eingaben so zu transformieren, dass sie mit der grünen Zielfigur übereinstimmt.1
Fügen Sie dazu der roten Figur Skripte hinzu, so dass die Figur mit den Pfeiltasten horizontal und vertikal bewegt werden kann (in 10-er Schritten), mit den Tasten “S” und “W” schrumpft oder wächst (in 10%-Schritten) und per Mausklick gedreht werden kann (in 30°-Schritten).
Außerdem soll die rote Figur beim Programmstart mit  auf ihren Initialzustand zurückgesetzt werden (Position (0, 0), Richtung 90°, Größe 100%).
auf ihren Initialzustand zurückgesetzt werden (Position (0, 0), Richtung 90°, Größe 100%).
 |
Aufgabe 6: App-Mockup entwickeln
Visuelle Entwicklungsumgebungen werden in der Praxis besonders zum Entwickeln von grafischen Benutzeroberflächen verwendet. Häufig werden dabei zunächst Prototypen oder “Mockups” erstellt, die keine wirkliche Funktionalität haben sondern nur simulierte, aber ähnlich aussehen wie das geplante Produkt und so einen ersten Eindruck von dessen Gestaltung und Bedienung vermitteln.
In dieser Aufgabe soll mit Scratch ein Mockup für eine Abstimmungs-App entwickelt werden. Hierbei reicht es, Anweisungen aus den Kategorien “Bewegung”, “Aussehen”, “Klang” und “Ereignisse” zu verwenden.
Laden Sie dazu die Projektdatei VotesApp.sb3 als Vorlage herunter: Download
Das Projekt besitzt vier Figuren (Smiley, Zeiger, Schaltflächen und ) und drei Hintergründe (Start-, Abstimmungs- und Ergebnisbildschirm).
 |
Der Startbildschirm soll beim Programmstart sichtbar sein. Durch Anklicken der Schaltfläche wird zum Abstimmungsbildschirm umgeschaltet. |
 |
Auf dem Abstimmungsbildschirm ist ein Smiley zu sehen, der die abzugebende Bewertung repräsentiert. Durch Anklicken kann zwischen den verschiedenen Smileys gewechselt werden. Durch Anklicken der Schaltfläche wird zum Ergebnisbildschirm umgeschaltet. |
 |
Auf dem Ergebnisbildschirm wird das Gesamtergebnis der Abstimmung durch den Zeiger angezeigt. In unserem Mockup soll der Zeiger einfach manuell durch die beiden Pfeiltasten und auf der Tastatur nach links oder rechts gedreht werden können. Durch Anklicken der Schaltfläche wird zum Abstimmungsbildschirm zurückgegangen. |
Das folgende Video demonstriert, wie die Anwendung verwendet wird:
Aufgaben
- Positionieren Sie die Figuren an den richtigen Stellen auf dem Bildschirm und erstellen Sie Skripte, so dass sich das Mockup wie oben beschrieben verhält.
- Beim Anklicken der Schaltflächen soll als akustisches Feedback ein Klickgeräusch abgespielt werden (Soundeffekt “Klick” der Objekte).
- Initial soll immer der Smiley ausgewählt sein. Wenn zwischen dem Abstimmungs- und Ergebnisbildschirm hin- und hergewechselt wird, soll sich der Zustand des Smileys nicht ändern.
- Der Zeiger soll beim Programmstart auf eine zufällige Richtung aus dem Bereich -145° bis 145° gesetzt werden. Dazu kann der folgende Werteblock verwendet werden, den Sie in der Kategorie “Operatoren” (grün) finden:

-
Ob das Ziel erreicht wurde, können wir momentan im Programm noch nicht automatisch überprüfen – in der nächsten Lektion werden wir Möglichkeiten dazu kennenlernen. ↩︎
1.3 Kontrollstrukturen
Bisher haben Sie in Scratch nur lineare Programmabläufe kennengelernt: Die bisherigen Programme bestehen aus Anweisungsfolgen, die durch Ereignisse ausgelöst und anschließend von der ersten bis zur letzen Anweisung sequenziell abgearbeitet werden.
So lassen sich allerdings nur vergleichsweise simple Lösungsverfahren umsetzen – meistens ist es nötig, vom sequenziellen Ablauf abzuweichen. Dazu werden nun Kontrollanweisungen eingeführt, die es ermöglichen, den Programmablauf zu steuern: Sie werden dabei die bedingte Ausführung von Programmabschnitten und die wiederholte Ausführung von Programmabschnitten kennenlernen und zur Lösung typischer Problemstellungen verwenden.
Grundlagen
Wenn wir ein Lösungsverfahren schrittweise formulieren, geben wir eine Folge eindeutiger, elementarer Handlungsanweisungen an. Eine solche eindeutige Handlungsvorschrift aus endlich vielen, wohldefinierten Einzelschritten wird als Algorithmus bezeichnet.
Als Beispiel soll eine Handlungsanleitung für ein Frage-Antwort-Spiel dienen. Hier kann die Handlungsfolge für die Moderatorin oder den Moderator so aussehen:
- Begrüße Gast
- Ziehe eine Fragekarte
- Stelle die Frage
- Nimm die Antwort entgegen
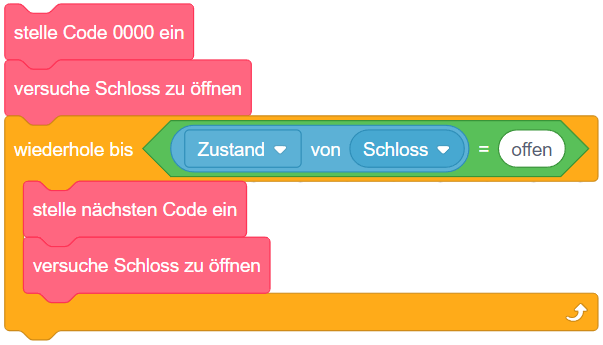
Dabei gelangen wir oft in die Situation, Anweisungen zu formulieren, die in Wiederholung ausgeführt werden müssen, bis eine bestimmte Bedingung erfüllt ist:
- Begrüße Gast
- Wiederhole bis Kartenstapel leer ist:
- Ziehe eine Fragekarte
- Stelle die Frage
- Nimm die Antwort entgegen
Die Sequenz der drei Anweisungen “ziehe Frage”, “stelle Frage”, “nimm Antwort entgegen” wird hier also wiederholt ausgeführt, bis die Bedingung “Kartenstapel leer?” erfüllt ist.
Außerdem gibt es Situationen, in denen eine Fallunterscheidung getroffen werden muss, die Ausführung einer oder mehrerer Anweisungen zu einem Zeitpunkt also von einer Bedingung abhängt – Falls A dann mache dies, anderenfalls mache jenes:
- Begrüße Gast
- Wiederhole bis Kartenstapel leer ist:
- Ziehe eine Frage
- Stelle die Frage
- Nimm die Antwort entgegen
- Falls die Antwort richtig ist:
- Sage “Richtig”
- Vergib einen Punkt
- Anderenfalls:
- Sage “Falsch”
Hier wird in jeder Wiederholung nach der Anweisung “nimm Antwort entgegen” überprüft, ob die Bedingung “Antwort ist richtig?” erfüllt ist und je nach Ergebnis entweder die Anweisungen “sage richtig”, “vergib Punkt” oder die Anweisung “sage falsch” ausgeführt.
Wiederholung und Fallunterscheidung (bzw. bedingte Anweisungen) stellen die beiden grundlegendsten Möglichkeiten dar, die Reihenfolge, in der Handlungsschritte eines Algorithmus abgearbeitet werden, zu steuern bzw. zu “kontrollieren”. Diese Konstrukte werden daher allgemein als Kontrollstrukturen bezeichnet. In der imperativen Programmierung werden sie durch spezielle Kontrollanweisungen umgesetzt. Wie das obige Beispiel zeigt, können diese Kontrollanweisungen auch in Sequenzen vorkommen und sogar ineinander geschachtelt werden, wodurch sich komplexe Algorithmen modellieren lassen. Im Folgenden werden wir uns mit verschiedenen Ausprägungen und Anwendungsfällen dieser beiden Kontrollstrukturen in Scratch beschäftigen.
Kontrollstrukturen in Scratch
In Scratch gibt es besondere Anweisungsblöcke zur Programmablaufsteuerung mittels Wiederholungen und Fallunterscheidungen, die Kontrollblöcke. Sie befinden sich in der Block-Bibliothek in der Kategorie “Steuerung” (orange). Das folgende Beispiel zeigt bedingte Anweisungen – wenn die Ausführung des Skripts bei diesem Kontrollblock ankommt, wird die Sequenz “spiele Klang”, “verstecke dich” nur dann ausgeführt, falls das Objekt zu diesem Zeitpunkt gerade den Mauszeiger berührt:
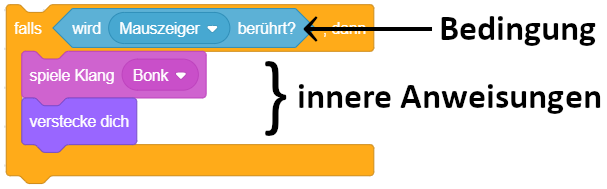
Kontrollanweisungen werden in Scratch allgemein durch Blöcke dargestellt, die wie “Klammern” aussehen (“Klammerblockform”):
Solche Klammerblöcke können andere Blöcke oder Sequenzen umschließen, indem diese einfach innerhalb der Klammer platziert werden. Der Kontrollblock bestimmt nun, ob oder wie oft die von ihm umschlossenen Blöcke ausgeführt werden. Daneben lassen sich Kontrollblöcke aber auch genau wie Anweisungsblöcke vertikal mit anderen Blöcken zu einer Sequenz verbinden:
Bedingungen in Scratch
Kontrollblöcke, deren Ausführung von einer Bedingung abhängt, besitzen ein sechseckiges “Loch” im Blockkopf – ähnlich den ovalen Eingabefeldern für Parameterwerte in anderen Blöcken. Bedingungen sind in Scratch entsprechend durch sechseckige Blöcke, die sogenannten “Wahrheitswerteblöcke” dargestellt, die in diese Eingabefelder eingefügt werden können – genau wie ovale Werteblöcke in die Parameter-Eingabefelder anderer Blöcke eingefügt werden können.
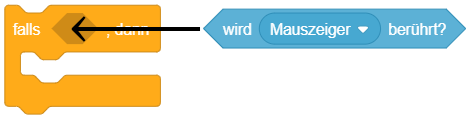
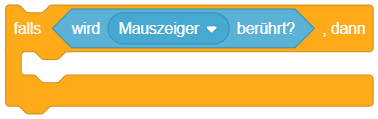
Ein Wahrheitswerteblock ist ein besonderer Werteblock, der nur zu den beiden Werten wahr oder falsch ausgewertet werden kann. Solche Werteblöcke werden mit einer sechseckigen Form statt einer ovalen Form dargestellt:
Scratch bietet eine Reihe von Wahrheitswerteblöcken an, um bestimmte Objekt- oder Systemzustände zu überprüfen, beispielsweise ob ein Objekt gerade den Mauszeiger, ein anderes Objekt oder eine bestimmte Farbe berührt oder ob eine bestimmte Taste gerade gedrückt ist:



Diese Wahrheitswerteblöcke befinden sich in der Kategorie “Fühlen” (türkis). Wenn Sie einen Wahrheitswertblock im Entwurfsmodus anklicken, zeigt er seinen momentanen Wert an (genau wie die ovalen allgemeinen Werteblöcke).
Daneben lassen sich auch Vergleiche zwischen Attributen und Werten als Bedingung angeben, beispielsweise “Ist die x-Koordinate des Objekts kleiner als 0?”. Dazu finden sich in der Kategorie “Operatoren” (grün) drei Wahrheitswerteblöcke für die Vergleichsoperationen “größer als”, “kleiner als” und “gleich”:



In die beiden ovalen Eingabefelder können beliebige (ovale) Werteblöcke eingefügt werden oder feste Werte eingetragen werden, die verglichen werden sollen. Sobald eine solche Bedingung im Programm ausgewertet wird, werden zunächst die momentanen Werte der inneren Werteblöcke abgefragt und verglichen. Der Block gibt dann je nach Vergleichsergebnis wahr oder falsch zurück (auf die Vergleichsoperatoren gehen wir später unter Logische Ausdrücke noch genauer ein).
Bedingte Anweisungen
Die Kontrollstruktur für Fallunterscheidungen wird in der imperativen Programmierung als bedingte Anweisung bezeichnet. In Scratch gibt es zwei Kontrollblöcke für bedingte Anweisungen, die so auch in so gut wie allen imperativen Programmiersprachen zu finden sind: Die Variante ohne Alternative (“falls … dann …”) und die Variante mit Alternative (“falls … dann … sonst …”).1
| Bedingte Anweisung ohne Alternative | Bedingte Anweisung mit Alternative |
|---|---|
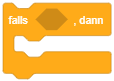 |
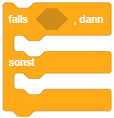 |
Als Beispiel für die Varianten der bedingten Anweisung dient hier die Umsetzung eines einfachen Frage-Antwort-Spiels in Scratch. Das vollständige Projekt Quiz.sb3 können Sie hier herunterladen: Download
Um Eingaben abzufragen und auszuwerten, werden hier zwei neue Blöcke aus der Kategorie “Fühlen” (türkis) eingeführt:
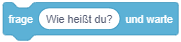 |
Die Anweisung “frage … und warte” zeigt eine Mitteilung an (wie bei “sage …”) und pausiert das Skript anschließend. Es erscheint ein Eingabefeld, in das eine Antwort eingegeben werden kann. Das Skript fährt erst dann fort, sobald die Eingabe mit der Eingabetaste abgeschlossen wird. |
 |
Anschließend kann der Werteblock “Antwort” verwendet werden, um die eingegebene Antwort auszuwerten. Der Wert des “Antwort”-Blocks ist immer die zuletzt bei einer Frage eingegebene Antwort. |
Bedingte Anweisung
Die einfachste Form der bedingten Anweisung führt die enthaltenen Anweisungen nur dann aus, falls eine bestimmte Bedingung erfüllt ist, anderenfalls nicht. Sobald der Programmablauf diesen Block erreicht, wird die Bedingung ausgewertet. Ist die Bedingung erfüllt, werden die enthaltenen Anweisungen ausgeführt. Anderenfalls fährt der Programmablauf nach dem Kontrollblock fort.
Im folgenden Beispiel wird zuerst eine Frage gestellt und anschließend nur dann die Mitteilung “Das ist richtig!” angezeigt, falls der Wert der Antwort mit dem Wert 31 übereinstimmt:
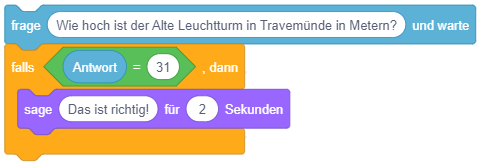
Bedingte Anweisung mit Alternative
Um eine einfache Fallunterscheidung umzusetzen (also “Falls A dann mache dies, anderenfalls mache jenes.”), wird die Variante der bedingten Anweisung mit Alternative verwendet. Dieser Kontrollblock besteht aus zwei “Klammern”: Sobald der Programmablauf diesen Block erreicht, wird die Bedingung ausgewertet. Ist die Bedingung erfüllt, werden die in der oberen Klammer enthaltenen Anweisungen ausgeführt. Anderenfalls werden die in der unteren Klammer enthaltenen Anweisungen ausgeführt. In beiden Fällen fährt der Programmablauf anschließend nach dem Kontrollblock fort.
Im folgenden Beispiel wird die Mitteilung “Das ist richtig!” angezeigt, falls der Wert der Antwort mit dem Wert 31 übereinstimmt, und anderenfalls die Mitteilung “Nein, das ist nicht richtig.”:
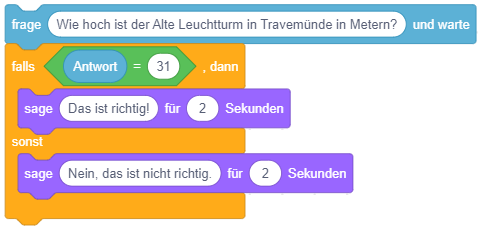
Mehrfache Fallunterscheidung
Eine mehrfache Fallunterscheidung – also eine Fallunterscheidung mit mehreren einander ausschließenden Fällen (“Falls A, dann mache dies, falls B dann mache das, falls C, dann mache jenes, …”) – lässt sich prinzipiell durch eine Sequenz von einfachen bedingten Anweisungen umsetzen, in denen jeweils einer der Fälle geprüft wird. Das folgende Beispiel unterscheidet die drei Fälle “Antwort = 31”, “Antwort > 31” und “Antwort < 31”, so dass bei einer falschen Antwort in Abhängigkeit davon, ob sie zu klein oder zu groß ist, eine unterschiedliche Mitteilung angezeigt wird:
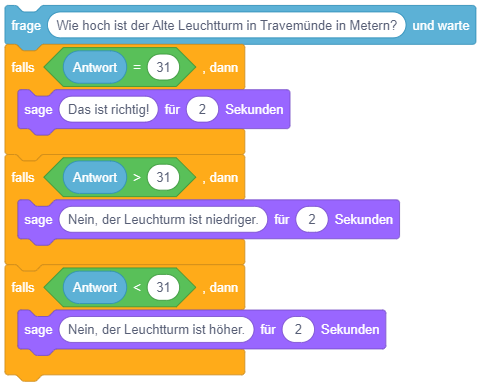
Dieses Konstrukt hat allerdings den Nachteil, dass unnötigerweise immer alle Bedingungen überprüft werden, auch wenn bereits die erste zutrifft. Schlimmer noch: Es kann sogar zu Fehlern bei der Programmausführung kommen, wenn bei der Ausführung des zutreffenden Falls die Bedingung der Fallunterscheidung verändert wird, wie das folgende Beispiel zeigt:
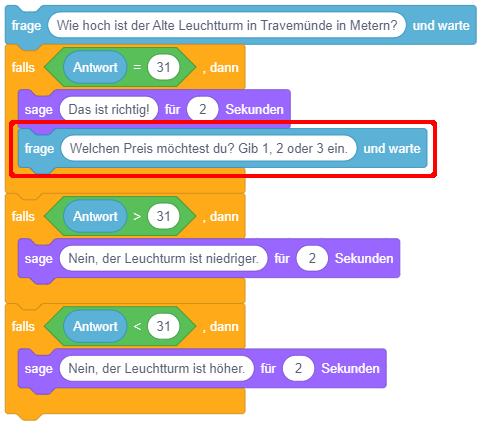
Wird hier zuerst 31 und anschließend eine Zahl zwischen 1 und 3 eingegeben, wird “versehentlich” auch der zweite Fall ausgeführt.
Sinnvoller ist hier die Strukturierung mittels verschachtelten einfachen Fallunterscheidungen: Um eine mehrfache Fallunterscheidung mit garantiert einander ausschließenden Fällen umzusetzen, können mehrere bedingte Anweisungen mit Alternative so ineinandergesetzt werden, dass die weiteren Fallunterscheidungen jeweils im alternativen Anweisungsteil vorkommen:
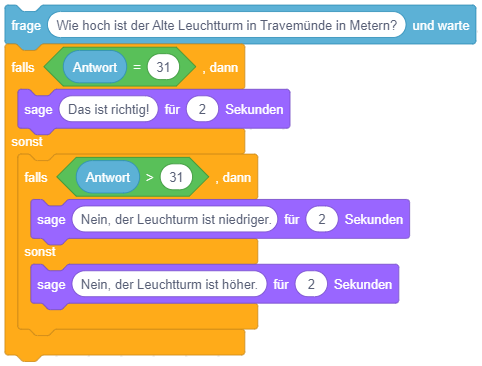
Hier wird die Bedingung “Antwort > 31” nur geprüft, falls “Antwort = 31” nicht zutrifft. Falls “Antwort > 31” ebenfalls nicht zutrifft, bleibt als letzte Möglichkeit “Antwort < 31” übrig.
🎓 Übung
- Laden Sie das unter Bedingte Anweisungen verlinkte Scratch-Projekt herunter und öffnen Sie es.
- Fügen Sie eine neue Frage hinzu. Duplizieren Sie dazu das Skript der Figur “Oktopus” und passen Sie es geeignet an.
- Passen Sie das Ereignis des duplizierten Skripts so an, dass es beim Wechsel zum Bühnenbild “Frage2” startet.
- Gestalten Sie das Bühnenbild von “Frage2” passend zu Ihrer Frage, wenn Sie möchten.
- Stellen Sie eine Frage, bei der es zwei richtige Antworten gibt.
- Bei einer falschen Antwort reicht es hier, einfach ohne weitere Fallunterscheidung “Nein, das ist nicht richtig.” anzuzeigen.
Wiederholungen
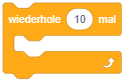
In Scratch gibt es drei Kontrollblöcke für Wiederholungen: Die Endloswiederholung, die Wiederholung mit fester Anzahl und die bedingte Wiederholung. Diese Kontrollstrukturen sind fester Bestandteil aller imperativen Sprachen, wobei manchmal auch nur die bedingte Wiederholung vorkommt, da sich die anderen Varianten der Wiederholung auch durch sie darstellen lassen (dazu später mehr).2
| Endloswiederholung | Wiederholung mit fester Anzahl | Bedingte Wiederholung |
|---|---|---|
 |
 |
 |
Endloswiederholung
Die einfachste Form der Wiederholung stellt die Endloswiederholung dar: Hier werden die enthaltenen Anweisungen (zumindest theoretisch) unendlich oft wiederholt nacheinander abgearbeitet. Die Wiederholung endet in Scratch erst, sobald das Programm explizit über das Symbol  abgebrochen wird.
abgebrochen wird.
Diese Kontrollstruktur eignet sich also für Aufgaben, die das gesamte Programm über (oder ab einem bestimmten Ereignis) permanent in Endlosschleife im Hintergrund ausgeführt werden sollen. Das folgende Beispiel setzt eine einfache Animation in Scratch um: Die einzelnen Grafiken (bzw. “Kostüme”) der Figur stellen die einzelnen Animationsschritte dar. Das Skript sorgt dafür, dass im Hintergrund permanent von einer Grafik zur nächsten gewechselt wird und so wie bei einem Daumenkinos der Eindruck einer flüssigen Animation entsteht. Durch die “warte”-Anweisungen wird hier eine Animationsrate von 8 Bildern/Sekunde umgesetzt.
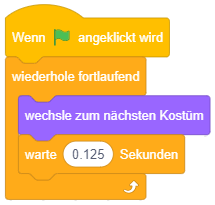
Es fällt auf, dass der “wiederhole fortlaufend”-Block unten flach ist, dort also keine weiteren Blöcke angehängt werden können. Warum? Sobald der Block im Programmablauf erreicht wird, werden die enthaltenen Blöcke in endloser Wiederholung ausgeführt – damit kommt der Ablauf niemals bei einer Anweisung nach diesem Kontrollblock an. Da also nachfolgende Anweisungen niemals ausgeführt werden können (in der Programmierung werden solche Programmteile als “toter Code” bezeichnet), ist es bei Scratch von vornherein gar nicht möglich, hier Programmteile anzufügen.
Um eine Endloswiederholung abzubrechen, wenn Sie nicht mehr benötigt wird, kann die Anweisung “stoppe dieses Skript” verwendet werden – beispielsweise falls die Stoppuhr 60 Sekunden seit Programmstart gezählt hat:
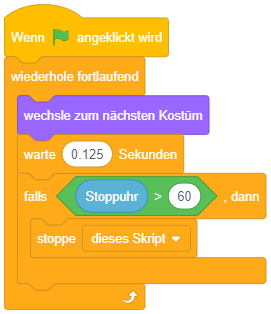
In der Regel ist es aber am sinnvollsten, Endloswiederholungen wirklich nur dann zu verwenden, wenn etwas während des gesamten Programmablaufs permanent wiederholt werden soll. Anderenfalls macht es Sinn, vorher darüber nachzudenken, wie lange die Wiederholung laufen soll und eine der beiden folgenden Varianten der Wiederholung zu wählen.
Wiederholung mit fester Anzahl
Die zweite Form der Wiederholung ermöglicht Abläufe, bei denen von vornherein feststeht, wie oft bestimmte Anweisungen wiederholt ausgeführt werden sollen. Die Anzahl der Wiederholungen wird hier als Parameterwert in das Eingabefeld eingetragen. Die umschlossenen Anweisungen werden genau so oft nacheinander ausgeführt, wie durch die Anzahl festgelegt ist.
Das folgende Beispiel setzt eine Bewegungsanimation um: Wird die Pfeiltaste nach oben gedrückt, soll die Figur hochspringen. Das Springen und anschließende Fallen wird hier durch je 5 Einzelschritte umgesetzt, in denen sich die Figur um jeweils 10 Pixel auf- oder abwärts bewegt. Vor dem Wechsel zum nächsten Schritt wird dabei jeweils kurz pausiert, um den Eindruck einer Stop-Motion-Animation zu erzeugen.
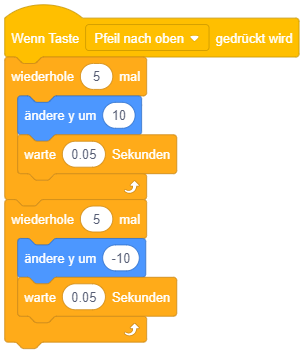
Solche Wiederholungen lassen sich zwar prinzipiell auch mittels Kopieren der enthaltenen Anweisungen durch eine einfache Sequenz ausdrücken (wie zum Teil in den Beispielen aus der letzten Lektion umgesetzt) – das sollte aber aus mehreren Gründen vermieden werden: Zum einen ist die Überarbeitung des Programms (z. B. zur Fehlerkorrektur) in solchen Fällen aufwendig, da eine Änderung an einer Anweisung in alle Kopien übernommen werden muss. Zum anderen wird der Code bereits ab einer geringen Anzahl von Wiederholungen unübersichtlich – von einer 100- oder 1000-fachen Wiederholung ganz zu schweigen. Darüber hinaus kann die Anzahl der Wiederholungen auch aus einem Werteblock abgefragt werden – eventuell entscheidet sich also erst zur Ausführungszeit, wie oft die Wiederholung durchlaufen werden soll.
Bedingte Wiederholung
Die beiden oben vorgestellten Varianten der Wiederholung kamen bisher ohne Bedingung aus, da die Wiederholungsanzahl jeweils von vornherein festgelegt war (n-mal bzw. unendlich oft). Die allgemeinste Form der Wiederholung führt die enthaltenen Anweisungen wiederholt nacheinander aus, bis eine bestimmte Bedingung erfüllt ist. Sie wird daher als “bedingte Wiederholung” oder präziser “Wiederholung mit Abbruchbedingung” bezeichnet.
So lässt sich beispielsweise die Endloswiederholung mit Abbruch, wenn die Stoppuhr 60 Sekunden gezählt hat, einfacher durch eine bedingte Wiederholung formulieren:
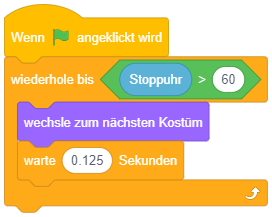
Dabei ist darauf zu achten, wann die Abbruchbedingung überprüft wird: Sobald der Programmablauf diesen Block erreicht, wird die Bedingung ausgewertet. Ist die Bedingung bereits zu diesem Zeitpunkt erfüllt, fährt der Programmablauf nach dem Kontrollblock fort, die enthaltenen Anweisungen werden übersprungen. Ist die Bedingung dagegen nicht erfüllt, werden die enthaltenen Anweisungen ausgeführt und der Programmablauf beginnt wieder am Anfang der Wiederholung. Die Bedingung wird erneut ausgewertet (dieses Mal könnte sie einen anderen Wert haben als bei der letzten Auswertung) und je nach Ergebnis wird eine weitere Wiederholung durchgeführt oder die Wiederholung beendet und nach dem Kontrollblock weitergemacht. Die enthaltene Anweisungssequenz wird also in jeder Wiederholung vollständig durchlaufen, bis die Bedingung das nächste Mal überprüft wird.
Da die Bedingung zu Beginn der Wiederholung überprüft wird, wird diese Art der bedingten Wiederholung auch “kopfgesteuerte Wiederholung” genannt.
Das folgende Beispiel modifiziert die Sprunganimation aus dem Beispiel zur Wiederholung mit fester Anzahl: Die Sprunghöhe soll nun davon abhängen, wie lange die Pfeiltaste gedrückt bleibt. Während zuvor also jeweils 5 Schritte auf- und abwärts gemacht wurden, soll die Figur sich nun solange aufwärts bewegen, bis die Pfeiltaste nicht mehr gedrückt ist, und anschließend fallen, bis ihre y-Koordinate wieder den Ausgangspunkt erreicht hat (hier -80).
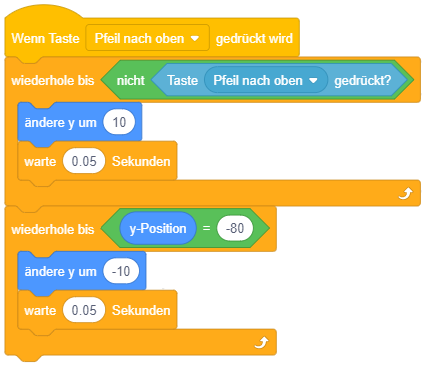
Hier wird ein neuer Operator verwendet, nämlich die Umkehrung bzw. Negation eines Wahrheitswertes mit dem “nicht”-Block.
🎓 Übung
- Öffnen Sie das Scratch-Projekt, das unter Bedingte Anweisungen entwickelt wurde.
- Passen Sie das Skript der Figur “Oktopus” so an, dass die Frage solange wiederholt gestellt wird, bis sie richtig beantwortet wurde.
Bedingtes Warten
In der Praxis tritt gelegentlich die Situation auf, dass ein Skript an einer bestimmten Stelle warten soll, bis eine bestimmte Bedingung erfüllt ist, bevor es mit der Ausführung fortfährt.
Als Beispiel: Ein Objekt soll erscheinen, sobald die Leertaste gedrückt wird, und danach wieder verschwinden, sobald die Leertaste nicht mehr gedrückt ist. Das Ereignis “Leertaste wird gedrückt” startet also ein Skript, in dem der Reihe nach
- zuerst das Objekt sichtbar wird,
- anschließend gewartet wird bis die Bedingung “Leertaste ist nicht gedrückt?” erfüllt ist,
- danach das Objekt wieder unsichtbar wird.
Diese Anforderung lässt sich durch eine bedingte Wiederholung lösen, deren Inhalt leer ist (es wird also wiederholt “nichts” gemacht, bis die Bedingung erfüllt ist):
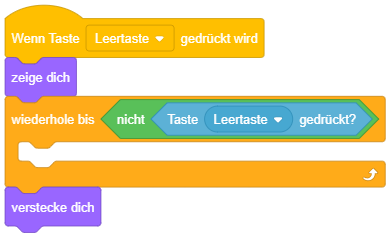
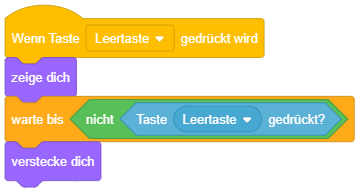
Hierfür bietet Scratch auch einen speziellen “warte bis”-Block an, der genau dieselbe Bedeutung hat wie ein “wiederhole bis”-Kontrollblock mit leerem Inhalt:
Wiederholte Zustandsabfrage
Bisher wurden Eingaben ereignisorientiert behandelt, also durch Skripte, die durch bestimmte Eingabeereignisse ausgelöst werden (“Taste/Maustaste wird gedrückt”). Diese Skripte werden potenziell parallel – also quasi gleichzeitig – ausgeführt, was den Nachteil hat, dass sich die Programmausführung so teils schwierig nachvollziehen lässt.
Mit Hilfe von Wiederholungen und bedingten Anweisungen lässt sich ein alternatives Konzept zur Eingabebehandlung umsetzen: Nach dem Programmstart wird einfach (ggf. endlos) wiederholt geprüft, ob bestimmte Tasten gedrückt sind oder nicht. Falls ja, wird entsprechend darauf reagiert – beispielsweise die Figur um 10 Pixel nach links verschoben, falls die linke Pfeiltaste gerade gedrückt ist oder um 10 Pixel nach rechts, falls die rechte Pfeiltaste gerade gedrückt ist.
Das folgende Beispiel zeigt ein Skript zur Bewegung einer Figur mittels wiederholter Abfrage (links) und zum Vergleich die ereignisorientierte Steuerung der Figur (rechts). Damit die Figur sich nicht zu schnell bewegt, wird die Abfrage hier in 0.05-Sekunden-Intervallen wiederholt durchgeführt – die Abfrage- und Schrittrate beträgt hier also 20 mal pro Sekunde. Beide Lösungen setzen prinzipiell dieselbe Steuerung um, bei der Ausführung fällt aber auf, dass die ereignisorientierte Variante im Vergleich zur wiederholten Abfrage etwas verzögert und weniger flüssig reagiert.
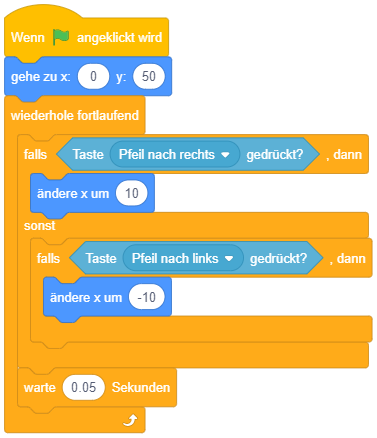
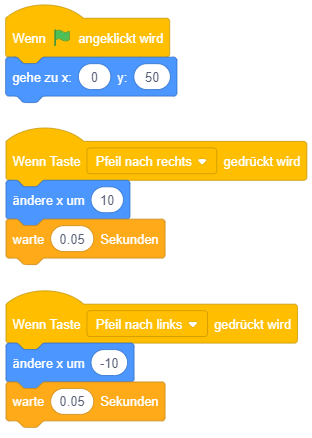
Dieses Prinzip, den Zustand von Eingabegeräten innerhalb einer Wiederholung zyklisch abzufragen, wird in der Informatik als Polling (engl. poll = abfragen) bezeichnet. Hierbei findet die Abfrage und Bearbeitung von Eingaben innerhalb eines einzelnen Skripts statt, was es einfacher macht, den Programmablauf zu kontrollieren als bei ereignisorientierter Eingabeverarbeitung, wobei mehrere Skripte parallel unabhängig voneinander ausgeführt werden (z. B. je ein Skript pro Taste, über welche eine Figur gesteuert werden kann). Polling erlaubt es in Scratch außerdem, auch auf Zustandsänderungen zu reagieren, für die keine Ereignisblöcke vorhanden sind (z. B. Maustaste wird an beliebiger Position gedrückt, zwei Objekte berühren sich), sofern es entsprechende Wahrheitswerteblöcke in der Kategorie “Fühlen” gibt.
🎓 Übung
- Laden Sie die Projektdatei Polling_vs_Ereignisse.sb3 herunter und öffnen Sie das Projekt in Scratch: Download
- Die obere Figur wird mittels Polling gesteuert (siehe Skript links), die untere Figur mittels Ereignissen (siehe Skript rechts). Starten Sie das Programm und vergleichen Sie in der Praxis, wie sich beide Figuren beim Drücken bzw. Gedrücktlassen der Pfeiltasten verhalten.
- Ändern Sie den Parameterwert der “warte”-Anweisung für die obere Figur (d. h. die Abfragerate), um ihre Bewegungsgeschwindigkeit zu erhöhen oder zu verringern.
Logische Ausdrücke
In den obenstehenden Beispielen haben wir bereits mehrere Operatoren verwendet, um Bedingungen aus mehreren Werten zu berechnen – zum einen Vergleichsoperatoren, zum anderen die Negation. In diesem Abschnitt werfen wir einen genaueren Blick auf zusammengesetzte logische Ausdrücke und logische Operatoren in Scratch.
Ein logischer Ausdruck ist – wie oben bereits beschrieben – ein Ausdruck, der zu einem Wahrheitswert (also wahr oder falsch, auch Boolesche Werte genannt) ausgewertet wird. Logische Ausdrücke können auch mit logischen Operatoren aus anderen Werten zusammengesetzt werden. In Scratch sind zwei Arten von logischen Operatoren vorhanden, Vergleiche von Werten (Zahlen oder Texte) und Verknüpfungen von Wahrheitswerten.
Vergleichsoperatoren
Vergleiche von Werten stellen logische Ausdrücke dar, z. B. kann das Ergebnis eines Ausdrucks wie “ist y kleiner als 0?” nur wahr oder falsch sein, je nachdem welchen Wert das Attribut y des betrachteten Objekts zum Zeitpunkt der Auswertung gerade hat.
In Scratch werden die mathematische Vergleichsoperatoren “größer als”, “kleiner als” und “gleich groß” unterstützt. Diese Operatoren werden durch Wahrheitswerteblöcke in der Kategorie “Operator” (grün) dargestellt.



Die Operanden, also die beiden Werte, die durch den Operator verglichen werden, können durch Werteblöcke angegeben werden, die in den beiden Eingabefeldern platziert werden, oder direkt als fester Wert angegeben werden, z. B. zum Vergleich der y-Koordinate eines Objekts mit dem Wert 0 (links) oder mit der y-Koordinate des Mauszeigers (rechts):


Verknüpfungsoperatoren
So lassen sich bisher allerdings nur einzelne Vergleiche als Bedingungen prüfen, aber nicht mehrere Vergleiche. Um mehrere logische Ausdrücke zu verknüpfen, werden logische Verknüpfungsoperatoren benötigt, also Rechenoperationen, die aus mehreren (meist zwei) Wahrheitswerten einen neuen Wahrheitswert berechnen. Die grundlegenden zweistelligen logischen Operatoren sind das logische UND, sowie das logische ODER. Daneben gibt es noch den einstelligen Operator NICHT zum Negieren eines Wahrheitswertes.



Konjunktion
Mit dem logischen UND (auch als Konjunktion bezeichnet), werden zwei logische Ausdrücke zu einem neuen Ausdruck verknüpft, der angibt, ob beide verknüpften Ausdrücke wahr sind, z. B. “(ist Taste Pfeil nach oben gedrückt?) UND (ist y kleiner als 0?)”.

A UND B ergibt genau dann WAHR, wenn beide Operanden den Wert WAHR haben.
Disjunktion
Mit dem logischen ODER (auch als Disjunktion bezeichnet), werden zwei logische Ausdrücke zu einem neuen Ausdruck verknüpft, der angibt, ob mindestens einer der verknüpften Ausdrücke wahr ist, z. B. “(ist Taste Pfeil nach oben gedrückt?) ODER (ist y kleiner als Maus y?)”. Das bedeutet also nicht, dass genau ein Ausdruck erfüllt ist (wie das umgangssprachliche “entweder A oder B”) – auch wenn beide verknüpften Ausdrücke wahr sind, ist der gesamte Ausdruck wahr.

A ODER B ergibt genau dann WAHR, wenn mindestens ein Operand den Wert WAHR hat.
Negation
Neben den beiden zweistelligen logischen Operatoren gibt es noch einen einstelligen Operator, die Negation bzw. das logische NICHT. Der Operand wird hier formal hinter den Operator geschrieben, z. B. “NICHT (wird Mauszeiger berührt?)” (statt des natürlich-sprachlichen “wird Mauszeiger nicht berührt?”).

NICHT A ergibt genau dann WAHR, wenn A den Wert FALSCH hat.
-
Bedingte Anweisungen werden im Deutschen meist als “wenn … dann” formuliert. Da das Wort “wenn” in Scratch allerdings bereits für Ereignisse verwendet wird (wobei hier “sobald” treffender wäre), wird im Kontext von Scratch zur besseren Unterscheidung das Wort “falls” für Fallunterscheidungen verwendet. ↩︎
-
Für die Wiederholungsstruktur ist im Deutschen auch der Begriff “Schleife” (von engl. loop) sehr verbreitet. Dieser Begriff wird im didaktischen Kontext allerdings kontrovers diskutiert, da er zu Fehlvorstellungen führen kann, wie beispielsweise die berüchtigte Wortschöpfung “if-Schleife” zeigt. In den Fachanforderungen wird daher der Begriff “Wiederholung” verwendet. Zur Diskussion siehe z. B. Ludger Humbert: Informatische Bildung – Fehlvorstellungen und Standards. In: Münsteraner Workshop zur Schulinformatik 2006, S. 37–46, Münster, 2006. ↩︎
1.3.1 Übungsaufgaben
Stoffwiederholung
Aufgabe 1: Scratch-Skripte interpretieren
Aufgabe 1.1: Objekt fangen
| Auf der Bühne befindet sich ein Objekt, das immer dann, wenn es mit dem Mauszeiger berührt wird, an eine andere zufällig ausgewählte Position auf der Bühne springen soll. |
Die folgenden Skripte stehen für das Objekt zur Auswahl. Geben Sie alle Skripte an, welche die Aufgabe richtig erfüllen (mindestens ein Skript ist richtig, möglicherweise auch mehrere).
Überlegen Sie auch, worin die Fehler in den anderen Skripten bestehen.
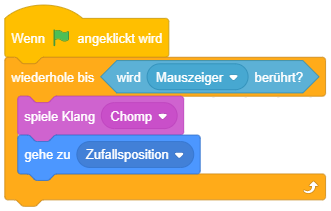 Skript 1 |
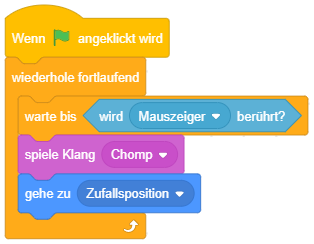 Skript 2 |
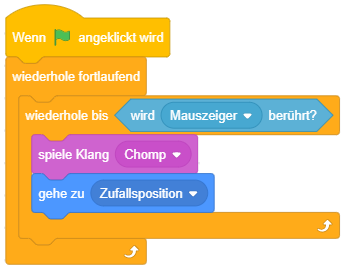 Skript 3 |
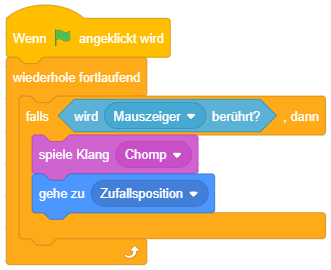 Skript 4 |
Aufgabe 1.2: Minigolf
| Ein Ball bewegt sich über die Bühne und prallt dabei vom Bühnenrand ab. Das Programm soll enden, wenn der Ball das schwarze Loch berührt. |
Die folgenden Skripte stehen für den Ball zur Auswahl. Geben Sie alle Skripte an, welche die Aufgabe richtig erfüllen (mindestens ein Skript ist richtig, möglicherweise auch mehrere).
Überlegen Sie auch, worin die Fehler in den anderen Skripten bestehen.
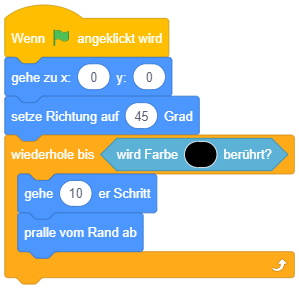 Skript 1 |
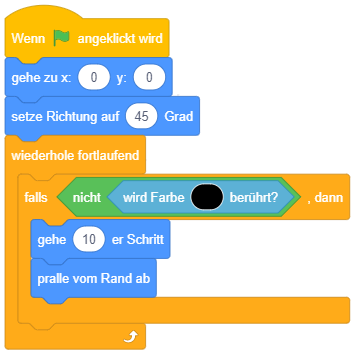 Skript 2 |
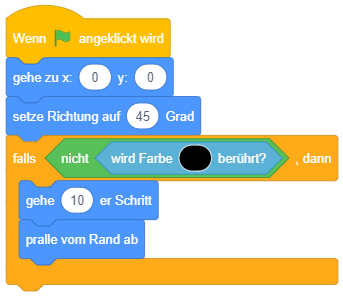 Skript 3 |
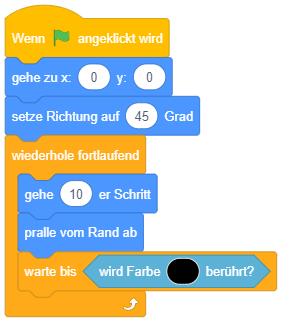 Skript 4 |
Aufgabe 1.3: Wrap-Around
| Eine Figur bewegt sich horizontal über die Bühne. Die Bewegungsrichtung kann mit den Pfeiltasten links/rechts festgelegt werden. Sobald die Figur den linken oder rechten Bühnenrand erreicht, soll sie auf der anderen Seite wieder auftauchen. |
Die folgenden Skripte stehen für die Figur zur Auswahl. Geben Sie alle Skripte an, welche die Aufgabe richtig erfüllen (mindestens ein Skript ist richtig, möglicherweise auch mehrere).
Überlegen Sie auch, worin die Fehler in den anderen Skripten bestehen.
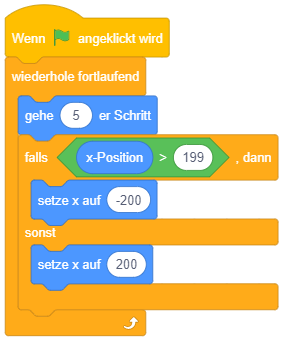 Skript 1 |
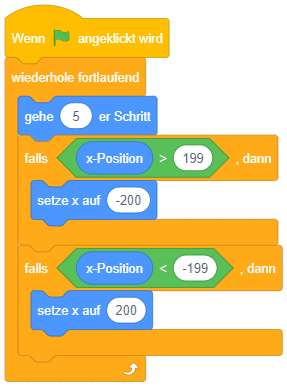 Skript 2 |
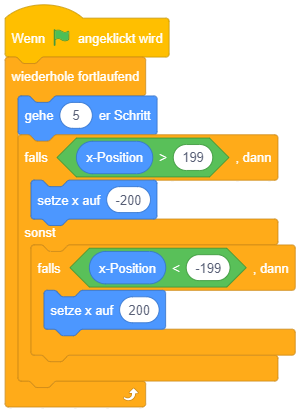 Skript 3 |
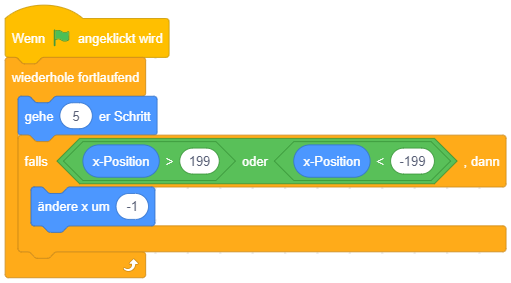 Skript 4 |
Aufgabe 1.4: Drehung um 360°
| Ein Zeiger soll sich innerhalb von einer Sekunde um 360° drehen, wenn er mit der Maus angeklickt wird. |
Die folgenden Skripte stehen für den Zeiger zur Auswahl. Geben Sie alle Skripte an, welche die Aufgabe richtig erfüllen (mindestens ein Skript ist richtig, möglicherweise auch mehrere).
Überlegen Sie auch, worin die Fehler in den anderen Skripten bestehen.
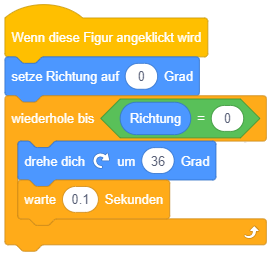 Skript 1 |
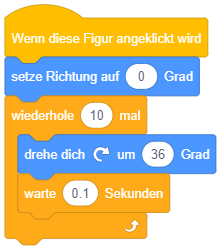 Skript 2 |
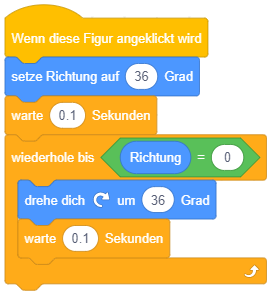 Skript 3 |
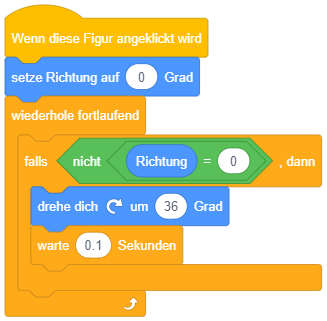 Skript 4 |
Aufgabe 2: Programmausführung nachvollziehen
In dieser Aufgabe soll der Ablauf eines Programms in Scratch nachvollzogen werden. Hier wird die Erweiterung “Malstift” verwendet, mit der ein Objekt eine Spur auf der Bühne zeichnet, während es sich bewegt:
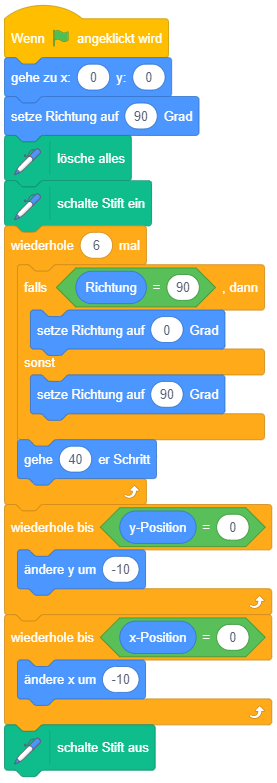
Skizzieren Sie die Zeichnung, die auf der Bühne entsteht, und beantworten Sie die folgenden Fragen:
- An welcher Position befindet sich der Stift am Ende?
- In welche Richtung zeigt der Stift am Ende?
- Wie oft wird die Anweisung “setze Richtung auf 0°” in der oberen Wiederholung ausgeführt?
- Wie oft wird die Anweisung “setze x auf x - 10” in der unteren Wiederholung ausgeführt?
Praktische Übungen
Aufgabe 3: 2D-Transformation überprüfen
In dieser Aufgabe soll die Anwendung zur Aufgabe 2D-Transformation aus der vorigen Übung um eine Ergebnisüberprüfung ergänzt werden.
Laden Sie dazu die Projektdatei 2D-Transformation.sb3 herunter: Download
Sobald die Leertaste gedrückt wird, soll nun überprüft werden, ob die Form der roten Figur mit der grünen Zielfigur übereinstimmt. In diesem Fall soll kurz die Mitteilung “Passt genau!” angezeigt werden. Anschließend soll die grüne Figur eine neue zufällig ausgewählte Position, Rotation und Größe annehmen (siehe Anweisungen im Startskript der Figur).
Anderenfalls soll eine Eigenschaft mitgeteilt werden, die noch nicht übereinstimmt, z. B. “Die Position stimmt nicht.”, “Die Größe stimmt nicht.” oder “Die Richtung stimmt nicht.”
 |
Zum Testen der Bedingungen sind hier die folgenden Blöcke hilfreich:



Der dritte Block ("… von …") sieht in der Blockbibliothek zunächst so aus: 
Dieser Block wird verwendet, um den Wert eines Attributs eines anderen Objekts oder der Bühne abzufragen. Über die linke Auswahlliste (Symbol ▾) kann das gewünschte Attribut (z. B. y-Koordinate) und über die rechte Auswahlliste das Objekt oder die Bühne ausgewählt werden.
Aufgabe 4: Navigation nach Farben
In dieser Aufgabe soll eine Simulation mit Fallunterscheidungen und Wiederholungen umgesetzt werden. Das Szenario ist folgendermaßen:
In einem Labyrinth aus quadratischen farbigen Kacheln befindet sich ein Roboter, der sich schrittweise eine Kachel vorwärts bewegen oder in 90°-Schritten drehen kann. Beim Starten des Programms befindet sich der Roboter auf der linken oberen weißen Kachel mit Blickrichtung nach rechts und beginnt loszufahren. Nach jedem Schritt prüft er die Farbe der Kachel, auf der er sich befindet: Bei einer blauen Kachel dreht er sich um 90° nach links, bei einer roten Kachel nach rechts. Befindet er sich auf einer schwarzen Kachel, dreht er sich um 180°. Wenn er es schafft, die grüne Kachel zu erreichen, ist er am Ziel angekommen: Jubel ertönt und das Programm endet.
Damit wir den Ablauf gut beobachten können, soll der Roboter nur 10 Schritte (Bewegung oder Drehen) pro Sekunde ausführen.
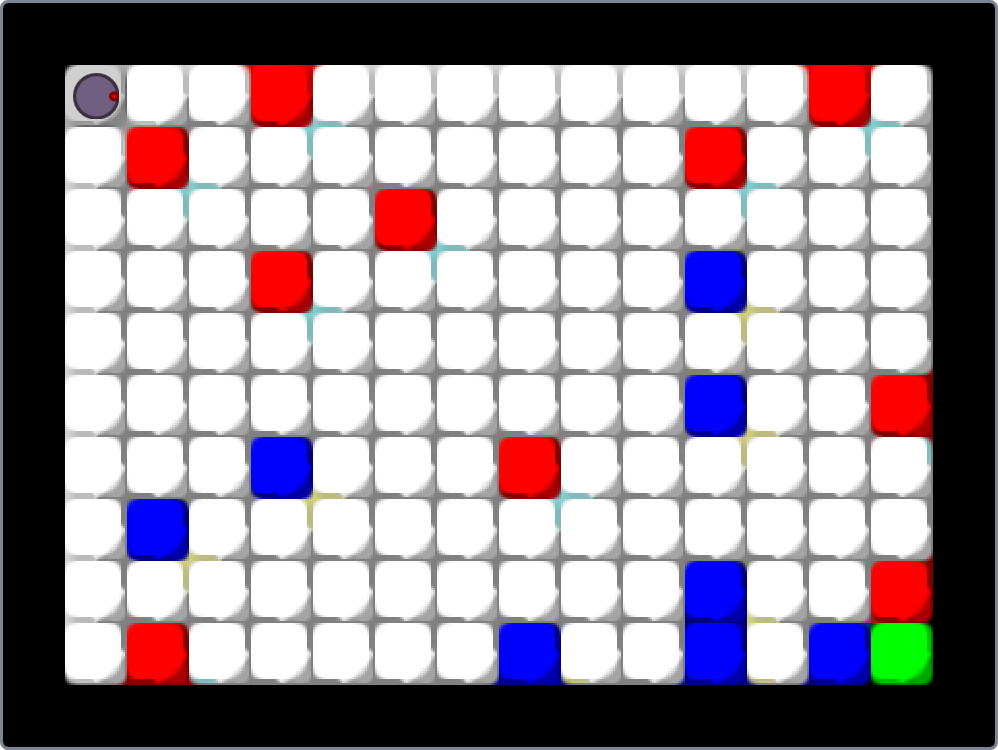 |
Laden Sie das Scratch-Projekt Farbnavigation.sb3 herunter: Download
Auf der Bühne finden Sie bereits alle Anweisungs- und Werteblöcke, die Sie zur Umsetzung der Lösung benötigen – es fehlen allerdings noch die Kontrollstrukturen.

Neu sind hier die Wahrheitswerteblöcke “wird Farbe berührt?” aus der Kategorie “Fühlen” (türkis). Diese Blöcke liefern den Wert wahr zurück, falls das Objekt momentan einen Punkt auf dem Bildschirm berührt, der die angegebene Farbe hat.
Überlegen Sie, wie die oben abgebildeten Anweisungen mit Hilfe von geeigneten Kontrollstrukturen zu einem Programm umgesetzt werden können, das den oben skizzierten Algorithmus für den Roboter umsetzt. Setzen Sie den Algorithmus in Scratch um und überprüfen Sie, ob der Roboter zum Ziel findet.
Zusatzaufgabe: Weg einzeichnen
Fügen Sie die folgenden Anweisungen aus der Erweiterung “Malstift” zum Projekt hinzu, um den Weg, den der Roboter zurücklegt, in das Labyrinth einzuzeichnen. Beim Starten des Programms sollten zunächst alle alten Malspuren beseitigt werden.



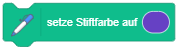
Wenn alles nach Plan läuft, sollte die Bühne nach der Ausführung des Programms folgendermaßen aussehen:
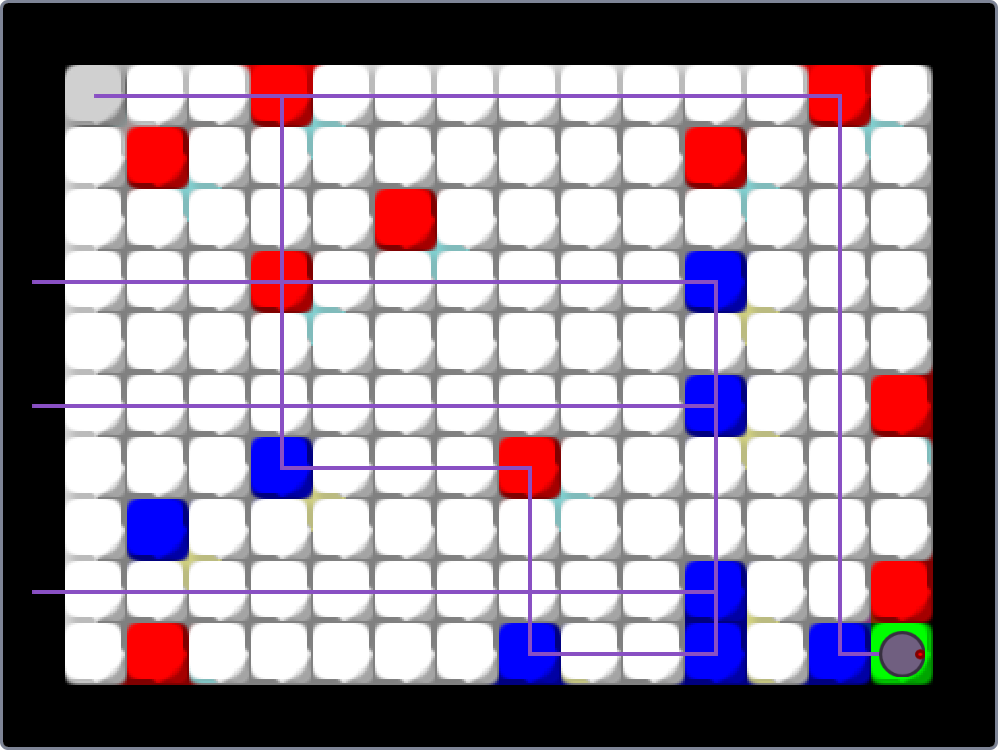
Aufgabe 5: Simulation eines Staubsaugroboters
In dieser Aufgabe soll eine weitere Simulation umgesetzt werden, dieses Mal allerdings ohne vorgegebene Blöcke. Hier soll das Verhalten eines Staubsaugroboters simuliert werden.1 Laden Sie dazu das Scratch-Projekt Staubsaugroboter.sb3 herunter: Download
Ein einfacher Staubsaugroboter funktioniert folgendermaßen: Er dreht sich zunächst in eine zufällige Richtung und fängt an, geradeaus zu fahren. Immer wenn er auf ein Hindernis stößt, fährt er ein Stück zurück (entgegen seiner Blickrichtung), dreht sich erneut in eine zufällige Richtung und fährt weiter geradeaus. So versucht er, jeden Winkel im Raum zu erreichen.
Der Roboter soll hier beim Programmstart in der Mitte der Bühne starten, nach der oben skizzierten Strategie herumfahren und dabei den Raum reinigen. Dazu zeichnet er, während er sich bewegt, eine helle Spur (z. B. in der Farbe des Bodens) hinter sich her, wobei die Stiftdicke etwas kleiner als sein Durchmesser gewählt wird. Die Raumwände sind durch schwarze Linien dargestellt.
Der Roboter kann dabei nicht endlos herumfahren, da sich sein Akku irgendwann erschöpfen würde. In diesem Programm soll der Roboter 30 Sekunden nach dem Programmstart anhalten.
Das folgende Bild zeigt, wie die Bühne ein paar Sekunden nach dem Start aussehen könnte (die Zeichenspur ist hier zur besseren Sichtbarkeit hellblau dargestellt):
 |
Neben den Blocktypen aus der vorigen Aufgabe Navigation nach Farben können die folgenden Blöcke für diese Aufgabe hilfreich sein:
 |
Dieser Werteblock liefert eine zufällige Ganzzahl zurück, die zwischen den beiden Parameterwerten liegt (hier z. B. zwischen 1 und 10). |
 |
Dieser Anweisungsblock setzt die Stoppuhr zur Zeitmessung auf Null zurück. |
 |
Dieser Werteblock liefert die Anzahl an Sekunden zurück, die seit dem Programmstart oder letzten Zurücksetzen der Stoppuhr vergangen sind. |
Setzen Sie den oben beschriebenen Algorithmus in Scratch um. Ermitteln Sie dabei experimentell geeignete Parameterwerte für die Bewegungsanweisungen und die zufällige Drehung bei Kollision mit einer Wand.
Aufgabe 6: Spielsteuerung ergänzen
In dieser Aufgabe soll ein kleines Spiel in Scratch vervollständigt werden. Laden Sie als Vorlage das Scratch-Projekt Flappy_Seagull.sb3 herunter: Download
Programm erkunden
In diesem Spiel wird eine Möwe gesteuert, die sich am linken Bildrand bewegt. Solange die Maustaste nicht gedrückt wird, fällt sie abwärts. Während die Maustaste gedrückt ist, steigt sie dagegen auf.
Ziel ist es, den gegnerischen Figuren auszuweichen, die am rechten Bildrand erscheinen und sich nach links bewegen (tatsächlich gibt es nur ein Gegnerobjekt, das nach dem Erreichen des linken Bildrands verschwindet und kurz darauf auf der rechten Seite wieder erscheint).
Untersuchen Sie zunächst die vorhandenen Skripte der Figuren und der Bühne.
Spielfigur bewegen
Ergänzen Sie das Skript der Spielfigur so, dass sie sich wie oben beschrieben verhält und gesteuert wird.
Setzen Sie die Steuerung dabei innerhalb des Wiederholungsblocks mittels “Polling” um.
Spielfigur animieren
Die Spielfigur soll während der gesamten Programmausführung fortwährend ihre Grafik wechseln, um den Eindruck einer Animation entstehen zu lassen.
Spielende
Das Spiel soll enden (Wechsel zum Hintergrund “Spielende”), wenn die Spielfigur das Gegnerobjekt berührt, oder wenn sie zu tief fällt und den unteren Bildrand erreicht.
Um zu prüfen, ob ein Objekt mit einem anderen kollidiert, kann der “Fühlen”-Block “wird … berührt?” verwendet werden (Auswahl des Zielobjekts über das Symbol ▾):

-
Diese Aufgabe basiert auf der Aufgabenstellung “Simulation eines Mähroboters” von Dr. Annika Eickhoff-Schachtebeck, Lehrerbildungszentrum Informatik, Universität Göttingen, lizensiert unter CC BY-NC-SA (https://www.uni-goettingen.de/de/629174.html) ↩︎
1.4 Programmieren mit Variablen
In dieser Lektion werden wir das Fachkonzept der Variablen in der Programmierung behandeln und uns detaillierter mit (u. a. mathematischen) Ausdrücken, Operatoren und Funktionen beschäftigen, um Werte aus anderen Werten zu berechnen.
Variablen
Bisher haben wir in unseren Programmen mit den von Scratch vorgegebenen Daten gearbeitet – im Wesentlichen die Attribute von Figuren und Bühne, sowie globale Werte wie Mauszeigerposition, Lautstärke, Wert der Stoppuhr oder Antwort auf die letzte Frage. Um diese Werte abzufragen, werden bestimmte Werteblöcke verwendet, und es gibt zum Teil bestimmte Anweisungsblöcke, um diese Werte zu verändern (z. B. “setze x auf …”).
In vielen Situationen ist es allerdings nötig, weitere Daten zu speichern, um mit Informationen zu arbeiten, sie sich während der Programmausführung ändern können – beispielsweise wenn Sie einen Punktezähler in ein Spiel einbauen möchten, die Anzahl der richtigen Antworten in einem Quiz mitgezählt werden soll, oder es eine einstellbare Geschwindigkeit für bewegte Objekte geben soll. Um beliebige Daten zu speichern und wieder abzurufen, werden in der Programmierung Variablen verwendet, deren Verwendungszweck wir selbst festlegen.
In Scratch können dazu neue, von uns benannte Werteblöcke definiert werden, sogenannte “Variablenblöcke”, in denen jeweils ein beliebiger Wert gespeichert werden kann. So lässt sich beispielweise ein neuer Werteblock namens “Punkte” erzeugen, dessen Wert mit einer bestimmten Anweisung (“setze Punkte auf …”) verändert werden kann. Dieser Werteblock lässt sich dann im Programm verwenden, um die aktuelle Punktezahl zu speichern, bei bestimmten Ereignissen zu erhöhen und auf der Bühne anzuzeigen.
Definition und Zuweisung
Eine neue Variable muss zunächst definiert werden. Dazu wird in Scratch die Schaltfläche “Neue Variable” in der Block-Kategorie “Variablen” ausgewählt und ein eindeutiger Bezeichner für die neue Variable vergeben – am besten ein aussagekräftiger Name, der angibt, was die Variable im Programm bedeutet (zum Beispiel “Tempo” für die Bewegungsgeschwindigkeit von Objekten). Anschließend erscheint ein neuer Werteblock mit dem Namen der neuen Variablen in der Block-Bibliothek. Durch Ankreuzen des Kästchens links neben dem Werteblock kann der Wert, der momentan in der Variablen gespeichert ist, live auf der Bühne angezeigt werden (wie wir es auch bereits von anderen Werten und Objekt-Attributen kennen).
Initial enthält jede neue Variable in Scratch den Wert 0. Um einen anderen Wert in der Variablen zu speichern wird der Anweisungsblock “setze Variable auf …” verwendet. Wenn diese Anweisung ausgeführt wird, speichert Sie den Wert, der für den Parameter angegeben wird, in der ausgewählten Variablen und überschreibt dabei den momentan vorhandenen Wert. Diese Anweisung wird als “Wertezuweisung” oder kurz Zuweisung bezeichnet. Das folgende Beispiel setzt den Wert der Variablen “Tempo” auf 25:
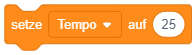
Um einen Wert zum aktuellen Wert der Variablen hinzuzuaddieren, kann auch die Anweisung “ändere Variable um …” verwendet werden (“inkrementelle Zuweisung”). Das folgende Beispiel zieht 5 vom aktuellen Wert der Variablen “Tempo” ab:
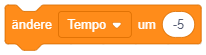
Als Parameter für die Zuweisung kann auch ein beliebiger Werteblock eingefügt werden (wie schon von anderen Anweisungen bekannt). In diesem Fall wird beim Ausführen der Zuweisung zunächst der momentane Wert dieses Werteblocks abgefragt und dieser Wert anschließend in die Variable geschrieben. So können auch Berechnungsergebnisse in einer Variablen gespeichert werden, hier beispielsweise die aktuelle x-Koordinate des Mauszeigers dividiert durch 10:


Der Variablenblock kann genau wie jeder andere Werteblock als Parameter in anderen Anweisungen verwendet werden. Wird die Anweisung ausgeführt, wird der momentan im Variablenblock gespeicherte Wert abgefragt. Hier wird beispielsweise der aktuellen Tempo-Wert zur x-Koordinate eines Objekts hinzuaddiert (links):
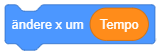
Genauso kann der Variablenblock auch als Operand in Operator-Werteblöcken verwendet werden, z. B. um zu prüfen, ob der aktuell gespeicherte Wert > 0 ist:

Globale Variablen und Objektvariablen
Bisher hatten wir Zustandswerte kennengelernt, die zu einzelnen Objekten gehören (die Attribute der Objekte, z. B. Position, Größe oder Kostümnummer) oder global sind, d. h. sich auf den gesamten Programmzustand beziehen (z. B. Position des Mauszeigers oder zuletzt eingegebene Antwort).
Variablen können ebenfalls als Objektvariablen oder globale Variablen definiert werden.
- Eine globale Variable gibt es nur einmal. Es kann also keine andere Variable mit demselben Namen geben. Jedes Objekt (bzw. konkreter: jedes Skript von jedem Objekt) kann den Wert einer globalen Variablen abfragen und durch Zuweisungen ändern. Globale Variablen werden also gemeinsam von allen Objekten genutzt.
- Eine Objektvariable gehört zu einem Objekt. Jedes Objekt hat seine eigenen Objektvariablen, auch wenn diese gleich heißen. Objektvariablen stellen also im Grunde selbst definierte Attribute dar. Andere Objekte können den Wert dieser Variablen zwar abfragen, aber nur Skripte des Objekts selbst können den Wert durch Zuweisungen ändern. Zur Unterscheidung von globalen Variablen werden sie im Kontext von Scratch daher auch als private Variablen oder lokale Variablen bezeichnet.1
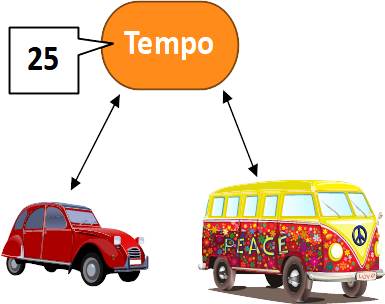 Globale Variable Tempo |
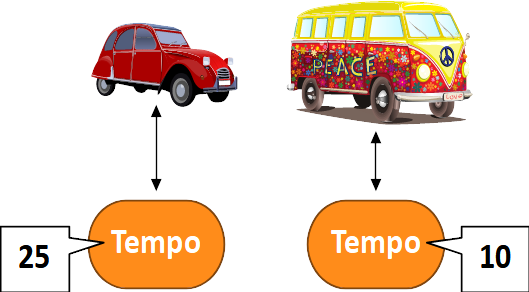 Objektvariablen Tempo von zwei verschiedenen Objekten |
Beim Erzeugen eines neuen Werteblocks über die Schaltfläche “Neue Variable” erscheint ein Dialog, in dem ausgewählt werden kann, ob eine globale Variable (“Für alle Figuren”) oder eine Objektvariable für die aktuell ausgewählte Figur (“Nur für diese Figur”) erzeugt werden soll:
Soll es nur einen Tempowert geben, die durch alle Objekte im Programm gemeinsam genutzt wird, sollte diese Variable global definiert werden. Wenn verschiedene Objekte dagegen eigene Tempowerte haben sollen, die unabhängig voneinander unterschiedlich sein können, sollte die Variable in jedem dieser Objekte privat definiert werden.
Zu beachten ist noch, dass zum Abfragen einer Objektvariablen im Skript eines fremden Objekts nicht der Variablenblock verwendet wird (private Variablenblöcke erscheinen nur in der Block-Bibliothek, wenn “ihr” Objekt ausgewählt ist), sondern der Werteblock “Attribut von Objekt” aus der Kategorie “Fühlen” – z. B. für eine Objektvariable “Tempo” des Objekts “Rennwagen”:

Um zu entscheiden, ob eine Variable global oder privat definiert werden soll, sollte also überlegt werden, ob die Variable nur innerhalb von Skripten eines bestimmten Objekts verwendet wird, oder ob sie von mehreren Objekten gemeinsam oder unabhängig von Objekten genutzt wird. Variablen, die nur innerhalb eines Objekts genutzt werden, sollten privat sein, damit sie nicht mit anderen Variablen verwechselt oder fälschlicherweise von anderen Objekten verändert werden. Dieses Konzept wird in der Programmierung als Datenkapselung bezeichnet.
Beispiel: Fische fangen
Als praktisches Beispiel zur Verwendung von Variablen dient hier ein kleines Point & Click-Spiel in Scratch. Laden Sie das Projekt Fische_Fangen.sb3 hier herunter: Download
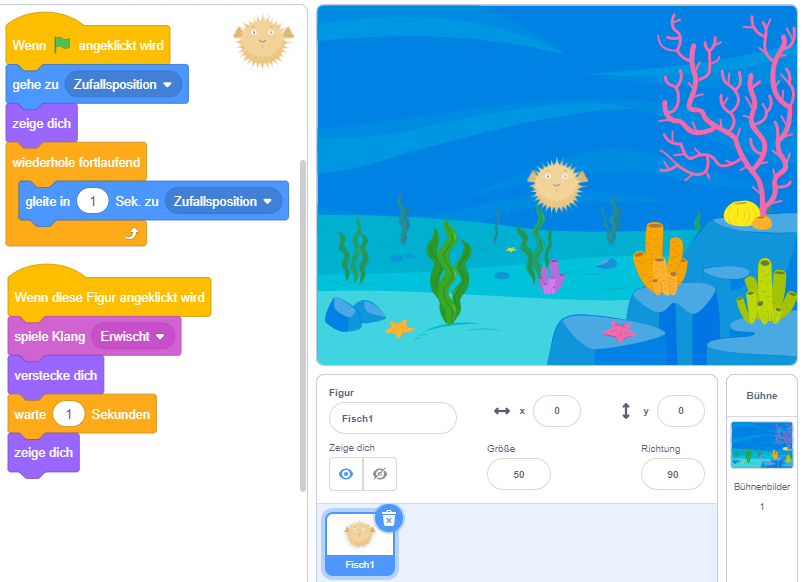
In diesem Spiel bewegt sich ein Fisch zufällig durch ein Aquarium und kann durch einen Mausklick gefangen werden. In diesem Fall verschwindet er und taucht dann eine Sekunde später an einer anderen Position wieder auf. Das Spiel soll nun durch Variablen folgendermaßen erweitert werden:
Punktestand
Es soll ein Punktezähler hinzugefügt werden. Jeder erfolgreiche Klick auf den Fisch soll mit einem Punkt belohnt werden. Der aktuelle Punktestand soll auf der Bühne angezeigt werden.
Dazu definieren wir zunächst eine neue Variable namens “Punkte”. Diese Variable kann als globale Variable angelegt werden (beim Anlegen der neuen Variablen “Für alle Figuren” wählen), da sie unabhängig von einem bestimmten Objekt ist.
Anschließend fügen wir die Anweisung “ändere Punkte um 1” zum Skript für das Ereignis “Wenn diese Figur angeklickt wird” hinzu, so dass bei jedem Mausklick auf den Fisch der Wert der Variablen “Punkte” um 1 hochgezählt wird:
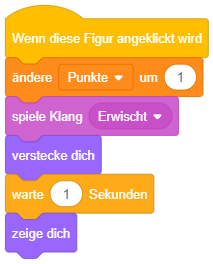
Damit wir den Punktestand während des Spiels sehen, muss das Kästchen links von der Variablen in der Block-Bibliothek angekreuzt werden:

Der Punktestand soll zu Beginn jedes Spiels auf 0 zurückgesetzt werden. Dieses Skript wird am besten zur Bühne hinzugefügt, da es einmal beim Programmstart ausgeführt werden soll und sich nicht auf bestimmte Objekte bezieht, sondern nur auf globale Werte (für solche Skripte ist die Bühne der beste Ort, da sie ebenfalls “global” ist):
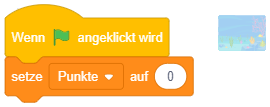
Treffer zählen
Der Fisch soll höchstens dreimal gefangen werden können. Beim dritten Klick auf den Fisch soll er verschwinden und anschließend nicht wieder auftauchen.
Wenn der Fisch angeklickt wird und danach nur noch einen Treffer übrig hat, soll er außerdem rot eingefärbt werden. Dazu kann der Block “setze Effekt Farbe auf -25” verwendet werden:

Um die Anzahl der bisherigen Treffer zu zählen, legen wir ein neue Variable namens “meine Treffer” an. Da diese Variable unmittelbar zum Objekt “Fisch1” gehört, definieren wir sie als Objektvariable (beim Anlegen der Variablen “Nur für diese Figur” auswählen). Sie stellt quasi ein neues Attribut des Objekts dar.
Außerdem ergänzen wir das Skript so, dass:
- der Trefferwert zu Beginn auf 3 gesetzt wird, (1.)
- der Trefferwert bei jedem Anklicken der Figur um 1 verringert wird, (2.)
- die Figur nach ihrem Verschwinden nur dann wieder auftaucht, falls noch Treffer übrig sind, (3.)
- und sie ihre Farbe ändert, falls der Trefferwert 1 erreicht. (4.)
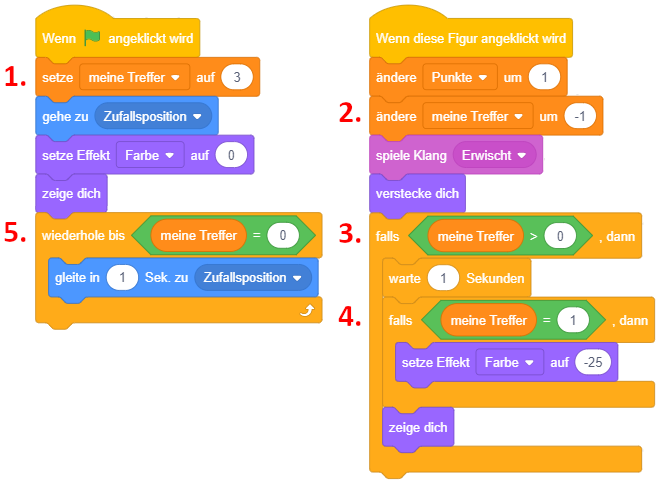
Um zu verhindern, dass das Objekt nach seinem letzten Verschwinden unnötigerweise unsichtbar weiter über die Bühne gleitet, wird die Endloswiederholung durch eine bedingte Wiederholung ersetzt, die endet, wenn der Trefferwert des Objekts 0 erreicht.
Nun möchten wir noch, dass mehrere Fische im Spiel vorhanden sind, die sich unabhängig voneinander bewegen. Das lässt sich einfach dadurch erreichen, dass das Objekt “Fisch1” in der Objektliste durch einen Rechtsklick dupliziert wird. Da die Variable “meine Treffer” als Objektvariable definiert wurde, hat jeder Fisch nun seine eigene Trefferanzahl. Hätten wir die Variable global definiert, würden sich alle Fische fälschlicherweise eine gemeinsame Trefferanzahl teilen.
Fachkonzept: Variable
Im allgemeinsten Sinne ist eine Variable in der Programmierung ein benannter Wertespeicher, der jeweils einen Wert zur Zeit speichern kann. Im Programmverlauf lässt sich lesend auf den Wert zugreifen oder der Wert überschreiben. Die Anweisung, um einen Wert in einer Variablen zu speichern, wird als Zuweisung bezeichnet. Der Wert einer Variablen kann beliebig oft durch Zuweisungen überschrieben werden (der Wert ist also “variabel”, daher auch die Bezeichnung).
Analogien für Variablen
Bildlich lassen sich Variablen anhand des “Tafel-Modells” (auch “Whiteboard-Modell”) gut veranschaulichen. Hier wird jede Variable durch eine kleine Tafel mit einem eindeutigen Namen repräsentiert, auf welcher der aktuelle Wert geschrieben steht. Initial steht auf jeder solchen Tafel hier der Wert 0. Bei jeder Zuweisung wird der aktuelle Wert auf der Tafel ausgewischt und durch den neuen Wert überschrieben.
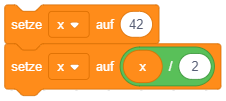
 Zustand der Variablen x zu Beginn |
  Ausführen der Zuweisung “setze x auf 42” |
  Ausführen der Zuweisung “setze x auf x / 2” |
Bei der letzten Zuweisung wird zuerst der momentan vorhandene Wert von x gelesen, um die Division x / 2 zu berechnen, und anschließend der vorhandene Wert durch das Divisionsergebnis überschrieben.
Diese Analogie erklärt auch anschaulich, was passiert, wenn einer Variablen der Wert einer anderen Variable zugewiesen wird: Hier wird einfach der Inhalt der anderen Tafel abgeschrieben.
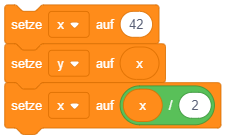
  Variablen x, y zu Beginn |
  Zuweisung “setze x auf 42” |
  Zuweisung “setze y auf x” |
  Zuweisung “setze x auf x / 2” |
Die letzte Zuweisung ändert hier also nur den Wert von x, nicht den Wert von y.
Typische Fehlvorstellungen
Andere Metaphern eignen sich nur bedingt, da sie anfällig dafür sind, bestimmte Fehlvorstellungen von Variablen zu entwickeln. Verbreitet sind neben dem “Tafel-Modell” etwa das “Behälter-Modell” (auch “Schubladen-Modell” oder “Schachtel-Modell”) oder die Analogie zu Variablen in der Mathematik.2
Die Vorstellung einer Variable als Kiste oder Schublade, die einen Zettel mit dem gespeicherten Wert enthält, kann zu der Fehlvorstellung führen, dass eine Variable eine Liste bzw. Historie aller jemals in ihr gespeicherten Werte enthält. Tatsächlich enthält eine Variable zu jedem Zeitpunkt nur einen Wert.
Durch das Gleichsetzen von Variablen in der Programmierung und Variablen in mathematischen Gleichungen kann die Fehlvorstellung entstehen, dass Variablen durch Zuweisungen wie y = x + 1 logisch miteinander verknüpft werden – also eine spätere Änderung des Wertes der Variablen x gleichzeitig den Wert der Variablen y ändert.
Ein weiterer beliebter Fehler besteht darin, dass Bezeichner und Wert einer Variablen verwechselt werden, dass also beispielsweise angenommen wird, der Vergleich einer Variablen namens x mit dem Buchstaben “x” muss zwangsläufig wahr ergeben, auch wenn die Variable einen ganz anderen Wert enthält (siehe auch unten unter Zeichenkettenausdrücke). Tatsächlich zählt aber bei Vergleichen oder Berechnungen mit Variablen nur deren aktueller Inhalt, der klar von ihrem Namen unterschieden werden muss.
Ausdrücke
Als Ausdruck wird in der Programmierung ein Konstrukt bezeichnet, das sich zu einem Wert auswerten lässt – in Scratch repräsentiert durch Werteblöcke – also beispielsweise mathematische oder logische Ausdrücke.
Ohne Variablen hatten wir Ausdrücke bisher nur zum Ermitteln von Parameterwerten für Anweisungen oder Vergleiche verwendet. Mit Variablen können Berechnungsergebnisse nun gespeichert und an späterer Stelle oder in einem anderen Skript wiederverwendet werden, wodurch komplexere Berechnungen möglich sind. Die folgende Anweisung berechnet zum Beispiel den Radius eines Kreises aus der zuvor eingegebenen Kreisfläche entsprechend der Formel \(r = \sqrt{\frac{A}{\pi}}\) und speichert das Ergebnis in der Variablen “Radius”:

Variablen können – wie oben gesehen haben – beliebige Werte speichern und sogar verschiedene Arten von Werten, beispielsweise Zahlen oder Texte. Die Arten von Werten werden als Datentypen bezeichnet. Üblicherweise wird eine Variable im Programm nur zum Speichern von Werten eines bestimmten Datentyps verwendet, die von ihrem Verwendungszweck abhängt (z. B. ganze Zahlen für eine Variable, die einen Punktestand darstellt oder die Anzahl richtiger Antworten zählt). Das ist aber nur eine Konvention – Variablen sind in Scratch aber nicht per se festgelegt auf einen bestimmten Datentyp.
Die Ergebnisse von Berechnungen hängen zum einen vom Operator (z. B. Divisionsoperator /) und zum anderen von den Werten der Operanden ab. Ob und wie ein Operator auf seine Operanden angewendet werden kann, hängt dabei auch von den Datentypen der Operanden ab, also welche Art von Wert sie haben. Beispielsweise macht es keinen Sinn, den Divisionsoperator / auf eine Zahl und einen Text anzuwenden. Das gilt auch für Parameterwerte von Anweisungen und Kontrollstrukturen: Die Kontrollstruktur “wiederhole … mal” erwartet beispielsweise eine Ganzzahl, die Anweisung “gehe … Schritt” eine Zahl.
Datentypen
Scratch unterscheidet die folgenden drei Datentypen für Werte:
- Zahlen: Zahlenwerte dienen als Operanden und Berechnungsergebnisse mathematischer Funktionen oder als numerische Parameterwerte für Anweisungen (z. B. “Wie viele Sekunden soll gewartet werden?”, “Wie oft soll wiederholt werden?”, “Um wie viel Grad soll gedreht werden?”). Sie können noch weiter unterschieden werden in Ganzzahlen und Dezimalzahlen (Achtung: Dezimalzahlen werden in Scratch nicht mit einem Komma geschrieben, sondern mit einem Dezimalpunkt, z. B. 3.1416).
- Zeichenketten: Zeichenketten (engl. string) sind Aneinanderreihungen von Zeichen wie Buchstaben, Ziffern, Satz- und Sonderzeichen und werden allgemein zur Darstellung von Texten verwendet (z. B. Fragen und Antworten, Namen, Mitteilungen).
- Wahrheitswerte: Die beiden Werte wahr oder falsch (auch: Boolesche Werte) werden für Bedingungen verwendet und können als Berechnungsergebnisse von Vergleichen und logischen Verknüpfungen entstehen.
Mathematische Ausdrücke
In Scratch stehen die gängigsten mathematischen Operatoren und Funktionen in der Kategorie “Operatoren” (grün) zur Verfügung:
    |
Wenn diese Blöcke abgefragt werden, geben Sie das Berechnungsergebnis für die beiden enthaltenen Werte an (Addition, Subtraktion, Multiplikation oder Division). |
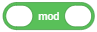 |
Wird dieser Block abgefragt, gibt er den Teilungsrest der ganzzahligen Division von a durch b an, wobei a und b die beiden enthaltenen Werte sind. |
 |
Wird dieser Block abgefragt, gibt er den enthaltenen Wert gerundet auf die nächste Ganzzahl an. |
 |
Wird dieser Block abgefragt, gibt er das Berechnungsergebnis für den enthaltenen Wert an, wobei verschiedene Funktionen ausgewählt werden können (über das Symbol ▾), u. a.: Betrag, ab-/aufrunden, Wurzel, Sinus, Kosinus, Tangens, Logarithmus und Exponentialfunktion. |
 |
Wird dieser Block abgefragt, gibt er eine zufällig ausgewählte Zahl zwischen a und b an, wobei a und b die beiden enthaltenen Zahlen sind. Wenn a und b beide Ganzzahlen sind, wird eine Ganzzahl ausgewählt, sonst eine Dezimalzahl. |
Die mathematischen Operatoren haben alle einen Zahlenwert als Ergebnis und erwarten generell Zahlenwerte als Operanden. Wird stattdessen eine Zeichenkette als Parameterwert verwendet, die nicht als Zahlenwert interpretiert werden kann, wird sie wie der Zahlenwert 0 behandelt, wie das folgende Beispiel zeigt:
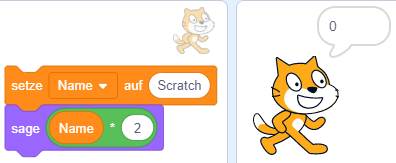
Zeichenkettenausdrücke
Für Zeichenketten gibt es eigene Werteblöcke in der Kategorie “Operatoren”, etwa um mehrere Zeichenketten verbinden oder um bestimmte Eigenschaften von Zeichenketten zu überprüfen:
 |
Wird dieser Block abgefragt, gibt er die Aneinanderhängung (Konkatenation) der beiden enthaltenen Zeichenketten-Werte an. Für “Apfel” und “Banane” wird beispielsweise die Zeichenkette “ApfelBanane” als Wert zurückgegeben. |
 |
Wird dieser Block abgefragt, gibt er das n-te Zeichen der angegebenen Zeichenkette an, wobei n die im linken Feld angegebene Zahl ist. Für die Werte 1 und “Apfel” wird beispielsweise das Zeichen “A” zurückgegeben. |
 |
Wird dieser Block abgefragt, gibt er die Länge der angegebenen Zeichenkette an, also die Anzahl ihrer Zeichen. Für “Apfel” wird beispielsweise der Zahlenwert 5 zurückgegeben. |
 |
Wird dieser Block abgefragt, gibt er als Wahrheitswert an, ob die links angegebene Zeichenkette die rechts angegebene Zeichenkette enthält. Groß- und Kleinschreibung spielt dabei keine Rolle. Für “Apfel” und “a” wird also wahr zurückgegeben, für “Apfel” und “PF” ebenfalls. Dabei muss die Reihenfolge der Operanden berücksichtigt werden – für links “fel” und rechts “Apfel” wird beispielsweise falsch zurückgegeben, andersherum dagegen wahr. |
Als Operanden können hier natürlich auch andere Werteblöcke und Variablenblöcke verwendet werden. Die Auswertung macht allerdings nur Sinn, wenn die Blöcke Werte der erwarteten Datentypen zurückgeben. Das folgende Beispiel speichert zunächst die Eingaben auf zwei “frage”-Anweisungen in den beiden Variablen namens “Nadel” und “Heuhaufen” und wertet dann die Bedingung aus, ob der Wert der einen Zeichenfolge in der anderen enthalten ist:
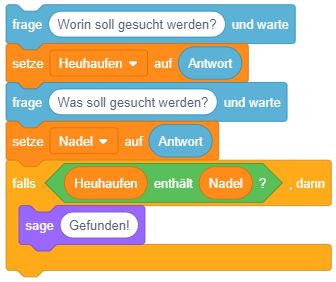
In diesem Beispiel liegt es nahe zu denken, dass die Bedingung niemals erfüllt sein kann, da die Zeichenkette “Nadel” ja nicht in der Zeichenkette “Heuhaufen” enthalten ist. Aber Achtung: Das sind die Namen der Variablen und nicht ihre Werte! Die Werte der Variablen sind hier die beiden Texte, die wir jeweils als Antwort auf die beiden “frage”-Anweisungen eingeben. Geben wir zum Beispiel bei der ersten Frage “Speisekammer” und bei der zweiten “Eis” ein, so wird in der Variablen namens “Heuhaufen” der Wert “Speisekammer” und in der Variablen namens “Nadel” der Wert “Eis” gespeichert, so dass die Bedingung “[Wert der Variablen] Heuhaufen enthält [Wert der Variablen] Nadel” zu wahr ausgewertet wird.
Wird ein Zahlenwert für einen Parameter verwendet, für den eine Zeichenkette erwartet wird, so wird er intuitiv als Zeichenkette interpretiert, wie das folgende Beispiel zeigt:
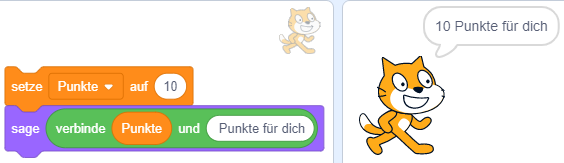
Logische Ausdrücke
In Lektion 2 haben wir bereits logische Ausdrücke kennengelernt, die als Bedingungen für die bedingte Wiederholung und Fallunterscheidung verwenden werden. Neben den Wahrheitswerteblöcken können mit Hilfe der logischen Operatoren auch logische Ausdrücke aus anderen Werten zusammengesetzt werden, etwa durch die Vergleichsoperatoren:



und die logischen Verknüpfungsoperatoren:



Die Operanden für die Vergleichsoperatoren können sowohl Zahlen als auch Zeichenketten sein. Der Datentyp der beiden Operanden sollte aber gleich sein. Die logischen Verknüpfungen erwarten dagegen Wahrheitswerte als Operanden. Das Ergebnis aller logischen Ausdrücke ist immer ein Wahrheitswert.
Anwendungsfälle für Variablen
Obwohl Variablen prinzipiell für beliebige Zwecke verwendet werden können, gibt es in der Praxis eine Reihe typischer Anwendungsfälle für Variablen, die wir teils hier bereits kennengelernt haben und teils in den praktischen Übungen vertiefen werden. Solche typischen Anwendungsfälle sind unter anderem:
- Zählen bestimmter Ereignisse oder Daten (“Zählvariable”), zum Beispiel: Wie viele Züge hat eine Spielfigur bereits gemacht, wie viele Wiederholungen wurden ausgeführt oder wie oft wurde eine bestimmte Taste gedrückt?
- Aufsummieren von Werten während der Programmausführung (“Akkumulatorvariable”), zum Beispiel: Es soll der Gesamtwert oder der Mittelwert eine Messreihe berechnet werden. Die Einzelmessungen werden hier in einer Variablen zusammensummiert und am Ende ausgegeben.
- Speichern von (Zwischen-)Ergebnissen von Berechnungen, die in mehreren Schritten durchgeführt werden
- Anlegen von “Sicherungskopien” von Werten zu einem bestimmten Zeitpunkt, die später benötigt werden und sich in der Zwischenzeit ändern könnten, zum Beispiel: die Antwort, die auf die letzte Frage eingegeben wurde (die anderenfalls bei der nächsten Frage verloren gehen würde)
- Informationen über Objekte oder das Programm, die sich im Laufe der Zeit ändern können, zum Beispiel: die momentane Bewegungsgeschwindigkeit oder Beschleunigung eines Fahrzeugs, der einstellbare Schwierigkeitsgrad eines Spiel
Beispiele
Das folgende Beispiel für eine Zählvariable zählt in der Variablen “Anzahl Mausklicks”, wie oft ein Objekt nach dem Programmstart angeklickt wird:

Das folgende Beispiel demonstriert eine Akkumulatorvariable “Summe Noten”. Hier wird die Summe von 10 Noten berechnet, um die Durchschnittsnote zu ermitteln:
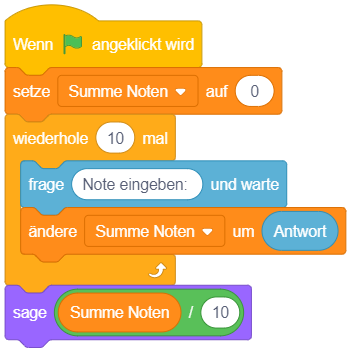
Variablen für Konstanten
Auch für Parameterwerte, die sich im Programmablauf selbst nicht ändern (also konstante Werte), kann es sich anbieten, den Wert in einer Variablen zu speichern, statt ihn direkt in die Anweisungen zu schreiben. So können Sie den Wert später schnell ändern, wenn sich herausstellt, dass er zu klein oder zu groß gewählt wurde. Anderenfalls müssten Sie den Wert manuell an jeder Stelle im Programm anpassen, an der er verwendet wird, was aufwendig und fehleranfällig ist.
Zum Beispiel: Alle Objekte im Spiel sollen mit 8 Bildern pro Sekunde animiert werden. Also hat jedes Objekt ein Skript der Form:
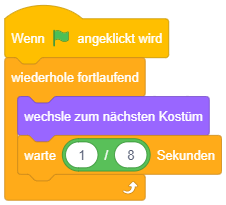
Stellen wir nun später fest, dass die Animationen zu langsam wirken, müssten wir den Parameterwert von “warte” in allen Skripten anpassen. Es ist also hilfreich, die Bildrate in einer globalen Variable zu speichern und deren Wert in allen Animationsskripten zu verwenden, statt einem festen Wert:

Die Variable können wir manuell mit dem Wert 8 belegen, indem wir den entsprechenden Block in der Block-Bibliothek anklicken, oder ihn zu Beginn des Startskripts der Bühne ausführen lassen:
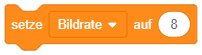
Um die Bildrate aller Animationen im Programm nun nachträglich zu verändern, reicht es, einmal den Wert der Variablen “Bildrate” anzupassen.
Überprüfen von Programmen
Um den Ablauf von Programmen oder Programmabschnitten, deren Verhalten von ihren Variablenbelegungen abhängt, besser nachvollziehen zu können und gegebenenfalls Fehler in der Programmierung zu finden, kann es hilfreich sein, die Wertebelegungen der Variablen über die Zeit zu protokollieren. Ein einfaches Werkzeug dafür stellen die sogenannten Trace-Tabellen dar.
Trace-Tabellen
Eine Trace-Tabelle (auch: Ablaufverfolgungstabelle) protokolliert die Änderungen von Variablenwerten während des Programmablaufs in tabellarischer Form. Jede Spalte stellt dabei eine Variable dar, deren Zustand beobachtet werden soll. Die Zeilen stellen diejenigen Anweisungen dar, durch die sich ein beobachteter Wert ändert – bei Variablen also also Variablenzuweisungen. Die Anweisungen werden dabei in der Tabelle zeilweise in genau der Reihenfolge dargestellt, in der sie während der Programmausführung abgearbeitet werden.
Neben Variablen lassen sich auch andere Werteblöcke (z. B. Attribute von Objekten, der Wert des “Antwort-Blocks) in der Tracetabelle beobachten, wenn sie für den Programmablauf relevant sind und sich ihre Werte während des Ablaufs ändern.
Der folgende Abschnitt eines Scratch-Skripts (links) berechnet die Summe von mehreren Noten, die nacheinander eingegeben werden, in der Variablen “Summe Noten”. Die Anzahl der Noten wird zu Beginn eingegeben und am Ende die Durchschnittsnote angezeigt. Um den Ablauf besser nachzuverfolgen, nummerieren wir hier die Zuweisungen und “frage”-Anweisungen von oben nach unten durch und listen die Nummer der Anweisung, auf die sich die Zeile bezieht, in der Trace-Tabelle mit auf (rechts).
Testhalber vollziehen wir den Ablauf hier für die folgende Sequenz von Eingaben bei den “frage”-Anweisungen nach: 4, 2, 1, 3, 3. Hier sollte also der Mittelwert der vier Noten 2, 1, 3 und 3 berechnet werden. Anhand der Trace-Tabelle lässt sich nachvollziehen, dass hier am Ende das Ergebnis von 9 / 4, also korrekterweise der Wert 2.25 angezeigt wird.
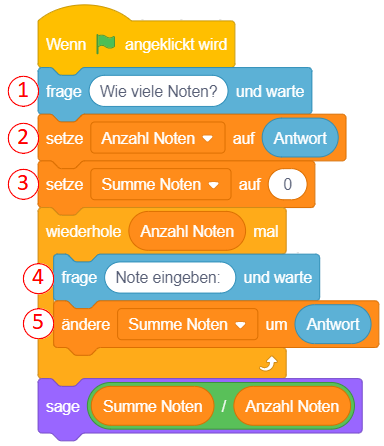
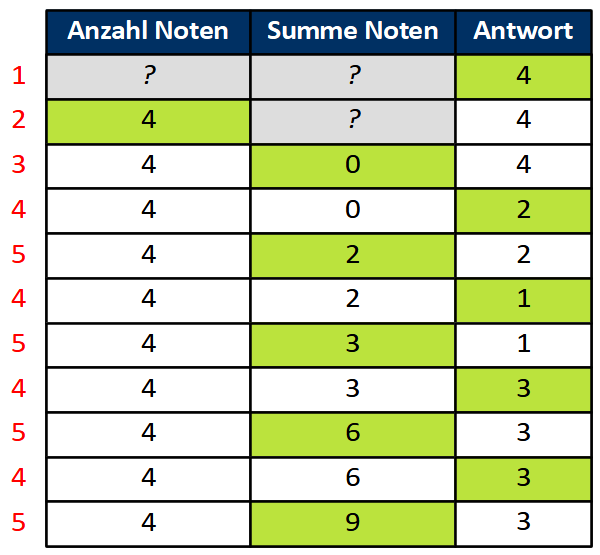
Hinweise zur Darstellung der Trace-Tabelle: Vor der ersten Zuweisung im beobachteten Programmabschnitt ist der momentane Wert der Variablen unbekannt (analog der Wert des “Antwort”-Blocks vor der ersten “frage”-Anweisung). Der Eintrag ? in der Trace-Tabelle kennzeichnet einen unbekannten Wert. Die hellgrün hinterlegten Felder kennzeichnen, dass ein Wert zugewiesen wird und den vorigen Wert überschreibt.
-
Die Begriffe “lokale Variable” und “private Variable” haben in der objektorientierten Programmierung üblicherweise eine andere Bedeutung, weswegen hier vorrangig der formal richtige Begriff “Objektvariable” verwendet wird. ↩︎
-
siehe Peer Stechert: Fehlvorstellungen und Modelle bei Variablen aus der Reihe Informatikdidaktik kurz gefasst (Teil 15), Video bei YouTube ↩︎
1.4.1 Übungsaufgaben
Stoffwiederholung
Aufgabe 1: Datentypen
In dieser Lektion haben wir verschiedene Datentypen von Werten identifiziert, nämlich Zahlen (Ganzzahlen und Dezimalzahlen), Zeichenketten (Texte) und Wahrheitswerte. Ausdrücke und parametrisierte Anweisungen erwarten in der Regel bestimmte Datentypen für ihre Parameterwerte. Werden trotzdem Werte von anderen Datentypen übergeben, werden diese zum erwarteten Datentyp uminterpretiert.
Datentypen für Parameter- und Rückgabewerte
Geben Sie für die folgenden Blöcke jeweils an, welche Datentypen für ihre Parameterwerte erwartet werden. Geben Sie bei den Werteblöcken ebenfalls an, welchen Datentyp der Rückgabewert hat (Zahl, Zeichenkette oder Wahrheitswert).
Überlegen Sie auch, ob in diesen Beispielen Parameter vorkommen, bei denen nur eine Ganzzahl als Wert sinnvoll ist (das heißt, Dezimalzahlen als Eingabe würden gerundet werden).
| Anweisungen und Kontrollstrukturen | |
|---|---|
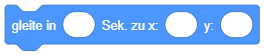 |
Parameter 1: ____________________________ Parameter 2: ____________________________ Parameter 3: ____________________________ |
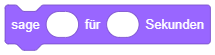 |
Parameter 1: ____________________________ Parameter 2: ____________________________ |
 |
Parameter 1: ____________________________ |
 |
Parameter 1: ____________________________ |
| Werteblöcke (Ausdrücke) | |
|---|---|
 |
Parameter 1: ____________________________ Parameter 2: ____________________________ Rückgabewert: ____________________________ |
 |
Parameter 1: ____________________________ Parameter 2: ____________________________ Rückgabewert: ____________________________ |
 |
Parameter 1: ____________________________ Parameter 2: ____________________________ Rückgabewert: ____________________________ |
 |
Parameter 1: ____________________________ Parameter 2: ____________________________ Rückgabewert: ____________________________ |
Aufgabe 2: Programm mit Variablen überprüfen
Das folgende Scratch-Skript ( Download) soll die Summe von mehreren nicht-negativen Messwerten (z. B. Zeit- oder Längenmessungen) berechnen, die nacheinander abgefragt werden. Die Abfrage wird durch Eingabe einer Zahl < 0 beendet. Diese Zahl soll dabei nicht mehr zur Summe dazugezählt werden, sondern dient nur dazu, dem Programm mitzuteilen, dass alle Messwerte eingegeben wurden. Zu Beginn wird außerdem noch nach der Maßeinheit gefragt (z. B. “ms” oder “cm”), die am Ende zusammen mit der berechneten Summe angezeigt wird.
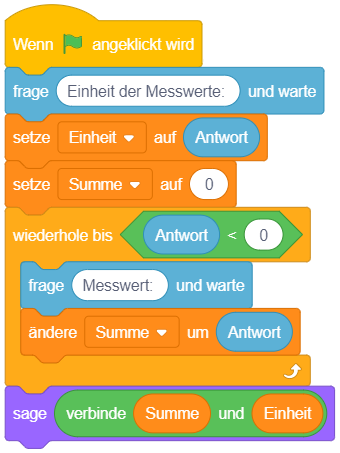
Trace-Tabelle erstellen
Vollziehen Sie den Ablauf des Skripts mit Hilfe einer Trace-Tabelle nach. Protokollieren Sie dabei die Werteänderungen der Variablen “Summe” und “Einheit”, sowie des Werteblocks “Antwort” während des Programmablaufs.
Gehen Sie dabei davon aus, dass der Reihe nach die folgenden Eingaben bei den “frage”-Anweisungen stattfinden: cm, 10, 12, 8, -1
Fehler korrigieren
Welcher Wert wird als Ergebnis erwartet und welcher wird am Ende angezeigt? Finden Sie anhand der Ergebnisse der Trace-Tabelle den Fehler im Skript und korrigieren Sie das Skript geeignet.
Aufgabe 3: Fehlvorstellungen zu Variablen
Das folgende Beispiel stammt aus dem Schulalltag:1 Beim ersten Aufruf der folgenden Sequenz wird 0 angezeigt. Die Schülerinnen und Schüler hatten aber mit 12 gerechnet. Beim zweiten Aufruf wird plötzlich wie erwartet 12 angezeigt. Jetzt sind alle vollständig verwirrt.
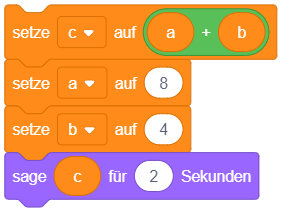
Erklären Sie das Szenario und erläutern Sie, welche Fehlvorstellung von Variablen dem Missverständnis zugrundeliegt. Geben Sie außerdem die korrekte Version der Sequenz an.
Praktische Übungen
Aufgabe 4: Kopfrechenquiz
Laden Sie das Scratch-Projekt Kopfrechenquiz.sb3 herunter und untersuchen Sie das Skript der Figur: Download
Das Projekt setzt ein einfaches Kopfrechenquiz um, in dem nacheinander ein Startwert und mehrere Rechenoperationen genannt werden, die im Kopf berechnet werden sollen. Die Abfolge der Rechenoperationen ist hier fest, für den Startwert und die Operanden werden aber jeweils zufällig ausgewählte Zahlen ausgegeben.
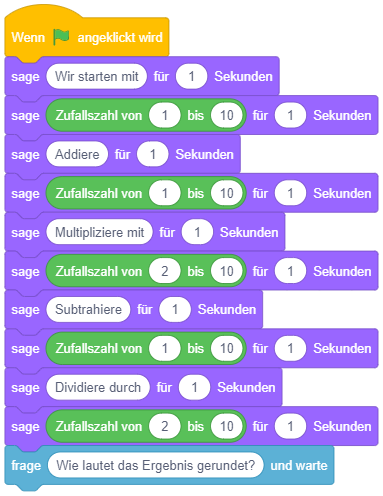 |
Das Quiz könnte also beispielsweise folgendermaßen ablaufen (die richtige Antwort wäre hier 8):
- Wir starten mit 4
- Addiere 8
- Multipliziere mit 5
- Subtrahiere 2
- Dividiere durch 7
- Wie lautet das Ergebnis gerundet?
Ergebnis überprüfen
Bisher gibt es noch keine Möglichkeit, das am Ende eingegebene Ergebnis zu überprüfen, da das erwartete Ergebnis momentan gar nicht vom Programm selbst berechnet wird.
Passen Sie das Skript also mit Hilfe von Variablen so an, dass das richtige Ergebnis begleitend zu den Ausgaben berechnet wird. Am Ende soll dann eine Rückmeldung gegeben werden, ob die eingegebene Antwort richtig oder falsch war.
Hilfreich für diese Aufgabe sind neben den Variablenblöcken die Operatorblöcke für mathematische Ausdrücke:





Aufgabe 5: Zeitmessung
Laden Sie das Scratch-Projekt Reaktionstest.sb3 herunter: Download
Das Programm stellt einen Reaktionstest dar: Der rote Kreis erscheint nach einer zufällig ausgewählten Zeit. Sobald er erscheint, wird die Stoppuhr auf Null zurückgesetzt. Sobald der Kreis nach seinem Erscheinen angeklickt wird, beginnt das Spiel von vorne: Die Stoppuhr wird zurückgesetzt, der Kreis verschwindet und wird nach einer zufällig ausgewählten Zeit wieder sichtbar. Ziel ist es, den Kreis so schnell wie möglich nach seinem Erscheinen anzuklicken. Wird zu früh geklickt oder statt des Kreises die Bühne angeklickt, endet das Spiel.
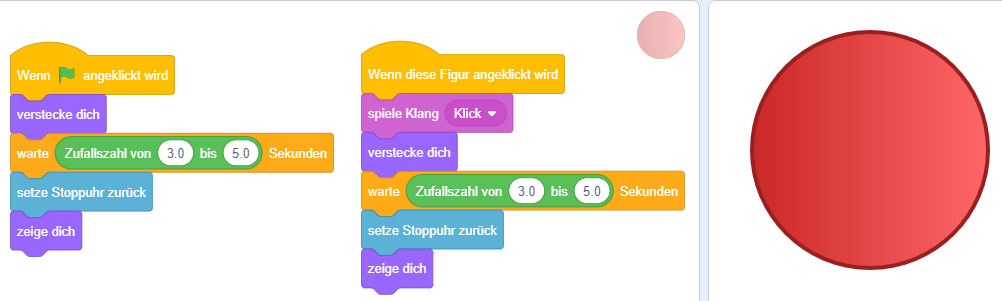
Durchschnittliche Reaktionszeit ermitteln
Passen Sie das Programm mit Hilfe von Variablen so an, dass die durchschnittliche Zeit, die benötigt wird, um den Kreis nach seinem Erscheinen anzuklicken, gespeichert und während der Programmausführung auf der Bühne angezeigt wird. Definieren Sie dazu ggf. weitere Hilfsvariablen.
Neben den Blöcken aus der Kategorie “Variablen” sind die folgenden Blöcke zur Zeitmessung für diese Aufgabe hilfreich:
 |
Dieser Anweisungsblock setzt die Stoppuhr zur Zeitmessung auf Null zurück. |
 |
Dieser Werteblock liefert die Anzahl an Sekunden zurück, die seit dem Programmstart oder letzten Zurücksetzen der Stoppuhr vergangen sind. |
Aufgabe 6: Spiel um Variablen ergänzen
In dieser Aufgabe soll das Spiel Flappy Seagull aus der vorigen Übung um mehrere Variablen ergänzt werden.
Laden Sie dazu das Scratch-Projekt Flappy_Seagull.sb3 herunter: Download
Die Figuren in diesem Spiel agieren mit einer Animationsrate von 20 Schritten pro Sekunde, da in der Wiederholung in den Skripten der Figuren am Ende jeweils 1/20 Sekunde gewartet wird.
Das Spiel soll nun um die folgenden Funktionen ergänzt werden:
- Die Möwe darf dreimal von der Gegner-Figur berührt werden, bevor das Spiel vorbei ist. Die Anzahl, wie oft sie noch berührt werden darf, soll dabei auf dem Bildschirm sichtbar sein.
- Wenn die Möwe berührt wird, soll sie für eine kurze Zeit vor weiteren Treffern geschützt sein. Der Schutz soll dabei 20 Animationsschritte andauern.
- Damit besser erkennbar ist, wann die Möwe geschützt ist, soll sie während dieser Zeit mit einer Transparenz von 50% angezeigt werden.
- Zusatzaufgabe: Führen Sie eine neue globale Variable für die Animationsrate ein, die von allen Figuren statt dem festen Wert von 20 Schritten pro Sekunde genutzt wird.
- Die Spielgeschwindigkeit soll während der Programmausführung anpassbar sein, indem mit den Pfeiltasten nach oben und unten der Wert der Animationsrate vergrößert und verringert wird (Achtung: Der Wert sollte nicht kleiner als 1 werden können!).
Das folgende Video demonstriert, wie das Spiel mit den Anpassungen aussehen könnte:
-
Quelle: Informationssammlung zur Informatikdidaktik der Pädagogischen Hochschule Schwyz: Fehlvorstellungen beim Programmieren, https://mia.phsz.ch/Informatikdidaktik/MisconceptionsInProgramming
der korrigierte Link zu Juha Sorva: Misconception Catalogue lautet http://urn.fi/URN:ISBN:978-952-60-4626-6 (Appendix A, S. 358 ff.) ↩︎
1.5 Strukturierung von Programmen
In den vorigen Lektionen haben wir Techniken kennengelernt, um eine Aufgabenstellung in kleinere Bausteine zu zerlegen, etwa in Abschnitte, die wiederholt oder bedingt ausgeführt werden, sowie Teilprogramme, die beim Eintreten bestimmter Ereignisse ausgeführt werden. In dieser Lektion werden wir selbst definierte Anweisungen (Unterprogramme/Methoden) und selbst definierte Ereignisse (Nachrichten/Signale) in Scratch einführen, um komplexere Programme zu strukturieren.
Ein Ziel der Programmstrukturierung ist es, Programme leichter lesbar zu machen und Code-Redundanzen zu vermeiden – also Programmteile, die als Kopie an mehreren Stellen im Programm vorkommen, was nicht nur den Programmumfang vergrößert, sondern auch zu Problemen führt: Soll nachträglich eine Änderung an einer Stelle im Programm vorgenommen werden, muss diese ggf. an mehreren anderen Stellen ebenfalls durchgeführt werden. Das ist zum einen zeitaufwendig, zum anderen potenziell fehleranfällig, da schnell eine Stelle übersehen werden kann.
Kommentare
Um umfangreichere Programme besser nachvollziehbar zu machen, kann es helfen, Programmabschnitte mit Kommentaren zu versehen, also kurzen Anmerkungen, in denen die Bedeutung eines Programmabschnitts zusammengefasst wird. In Scratch lassen sich Kommentare durch einen Rechtsklick in den Skriptbereich in Form von “Notizzetteln” einfügen.
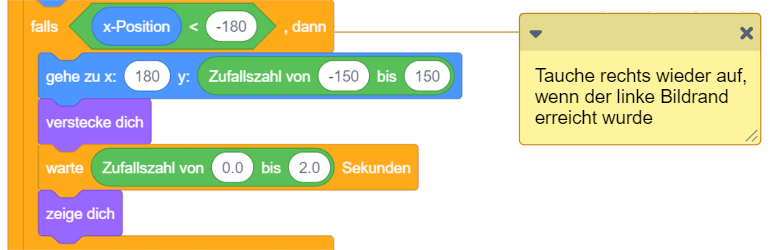
In so gut wie allen moderen Programmiersprachen ist es möglich, Textkommentare zum Quellcode hinzuzufügen.
Unterprogramme
Komplexere Programm können schnell unübersichtlich werden. Insbesondere kann es vorkommen, dass bestimmte Programmabschnitte zum Lösen derselben Aufgabe an mehreren Stellen vorkommen, was den Programmumfang unnötig vergrößert.
Als anschauliches Beispiel dient hier das Grundgerüst für ein Jump & Run-Spiel in Scratch. Laden Sie das Projekt Jump_and_Run.sb3 hier herunter: Download
In diesem Spiel wird eine Figur gesteuert, die sich mit den Pfeiltasten nach links und rechts bewegen lässt und außerdem springen kann.
 |
Das Springen der Figur kann durch mehrere Ereignisse ausgelöst werden:
- Als Eingabe wird die Pfeiltaste nach oben gedrückt oder die Figur wird mit der Maus angeklickt.
- Die Figur berührt den Stein. Hier wird die Figur anschließend auf die Startposition zurückgesetzt.
Die Aktion “springen” besteht dabei aus zwei Wiederholungen für die Auf- und Abwärtsbewegung, die innerhalb einer bedingten Anweisung stehen (“Befindet sich die Figur momentan auf dem Boden?”). Der entsprechende Programmabschnitt kommt also an drei verschiedenen Stellen im Programm in exakt gleicher Form vor:
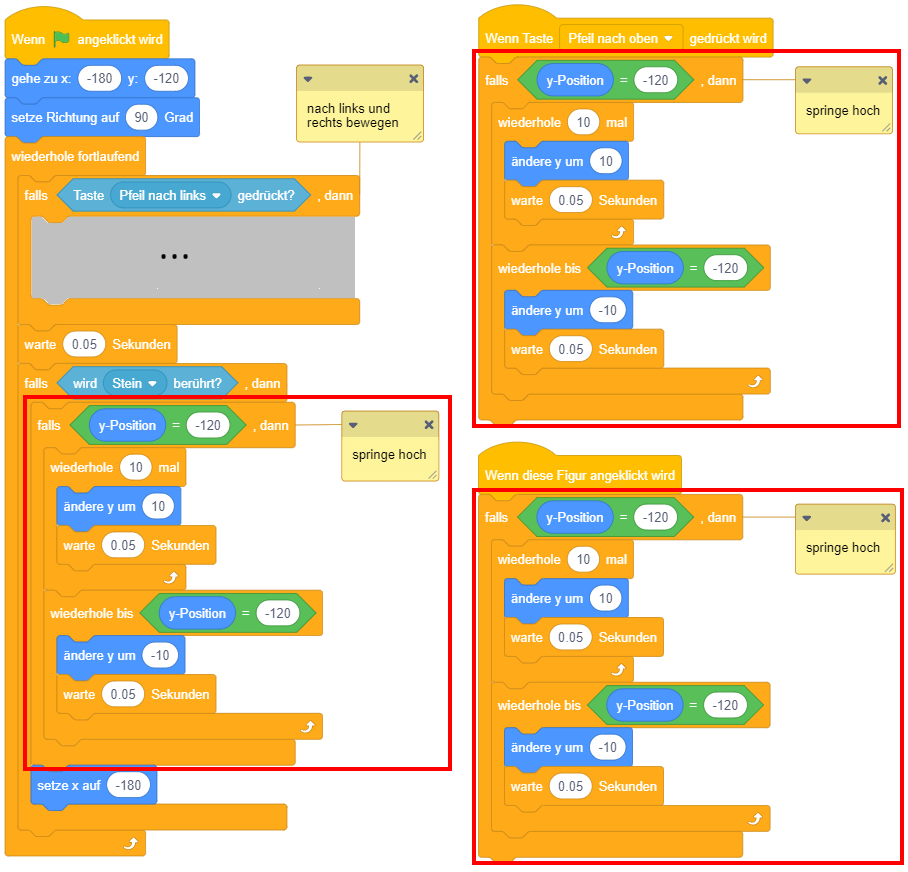
Um den Umfang des Programm zu verringern wäre es also hilfreich, die Anweisungen der “springen”-Aktion zu einer neuen Anweisung zusammenzufassen. Das lässt sich in Scratch mit Hilfe selbst definierter Blöcke umsetzen. Ein solcher “eigener” Block definiert ein Unterprogramm, das von anderen Skripten des Objekts mit Hilfe eines speziellen Anweisungsblocks ausgeführt werden kann. Ein Unterprogramm, das zu einem Objekt gehört, wird auch als Methode dieses Objekts bezeichnet.
Unterprogramme definieren und aufrufen
Ein Unterprogramm muss zunächst definiert werden. Dazu wird in Scratch die Schaltfläche “Neuer Block” in der Kategorie “Meine Blöcke” (rot) ausgewählt und ein eindeutiger Bezeichner für den neuen Block vergeben. Wie bei eigenen Variablen sollte der Bezeichner möglichst aussagekräftig sein (hier zum Beispiel “springe”). Anschließend erscheint ein neuer Anweisungsblock in der Block-Bibliothek unter “Meine Blöcke”.
Außerdem erscheint im Skriptbereich des Objekts ein neuer Definitionsblock, der wie Ereignisblöcke eine “Kopfblockform” hat:

An diesen Block können nun die Anweisungen des Unterprogramms angehängt werden. Der neue Anweisungsblock kann nun in anderen Skripten des Objekts zum Aufruf des Unterprogramms verwendet werden. Wenn dieser Block ausgeführt wird, werden die Anweisungen im Unterprogramm ausgeführt. Das aufrufende Skript pausiert dabei, bis das Unterprogramm zuende ausgeführt wurde und fährt danach erst fort.
Damit lässt sich das Beispielprogramm deutlich vereinfachen: In diesem Fall wird die Anweisungssequenz, welche die Sprung-Aktion darstellt, als Skript an den Definitionsblock angehängt. An den drei Programmstellen, an denen die Sprung-Aktion ausgeführt werden soll, wird nun stattdessen nur der selbst definierte Anweisungsblock “springe” eingefügt:
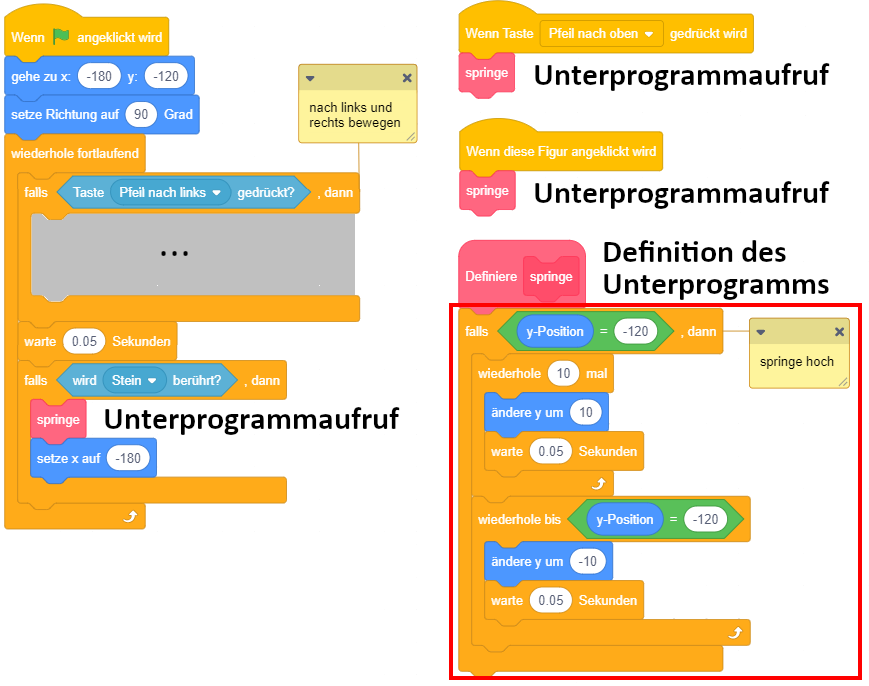
Im aufrufenden Skript sieht der Aufruf des Unterprogramms nun also genauso aus wie jede andere elementare Anweisung (z. B. “gehe zu Position”, “setze Richtung auf”, “warte”). Das Unterprogramm “verkapselt” dabei die eigentlichen Anweisungen, die beim Aufruf ausgeführt werden. Solange wir wissen, was der Effekt des Anweisungsblock ist (in diesem Fall “führe innerhalb von 1 Sekunde eine Sprungbewegung aus, falls die Figur sich auf dem Boden befindet”), können wir den Block zur Programmierung verwenden ohne genau wissen zu müssen, wie dieser Effekt konkret umgesetzt wird.
Ein Unterprogramm ist also allgemein ein wiederverwendbarer Programmabschnitt, der an anderen Stellen im Programm aufgerufen werden kann, um eine bestimmte Aufgabe zu übernehmen. Wir unterscheiden dabei die Definition des Unterprogramms (“Was macht es?”) vom eigentlichen Aufruf des Unterprogramms (“Mach es!”).
Unterprogramme mit Parametern
Oft sind Programmabschnitte zum Lösen bestimmter Aufgaben, die an verschiedenen Stellen im Programm vorkommen, nicht exakt identisch, sondern hängen von bestimmten Werten ab. Als Beispiel: Angenommen, die Sprung-Aktion aus dem vorigen Abschnitt soll mit verschiedenen Sprunghöhen durchgeführt werden – beim Drücken der Pfeiltaste oder Maustaste soll die Figur 10 Schritte hoch springen, beim Berühren des Steins dagegen nur 5 Schritte. Das Unterprogramm hängt nun also von einem Parameter ab, in diesem Fall der Sprunghöhe.
Zu diesem Zweck lassen sich parametrisierte Unterprogramme, also Unterprogramme mit Parametern definieren. Beim Aufruf eines parametrisierten Unterprogramms werden – genau wie bei den bisher bekannten parametrisierten Anweisungen in Scratch1 – verschiedene Parameterwerte angegeben, die bei der Ausführung des Unterprogramms berücksichtigt werden können. Dazu müssen beim Erstellen eines eigenen Blocks im Dialog “Neuer Block” entsprechende Eingabefelder für Parameter angelegt werden. Dabei stehen ovale Eingabefelder für Zahlenwerte und Zeichenketten, sowie sechseckige Eingabefelder für Wahrheitswerte zur Verfügung:
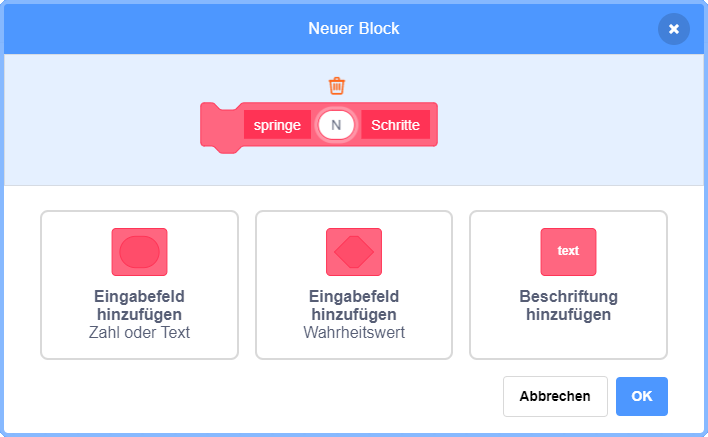
In diesem Beispiel wird ein ovales Eingabefeld namens “N” für die Anzahl der Sprungschritte hinzugefügt.2 Im Unterprogramm-Skript wird nun der Wert des Parameters N (statt wie zuvor der feste Wert 10) in der ersten Wiederholung verwendet. Dazu muss der entsprechende Werteblock  für diesen Parameter aus dem Definitionsblock in das Eingabefeld der Wiederholung gezogen werden:
für diesen Parameter aus dem Definitionsblock in das Eingabefeld der Wiederholung gezogen werden:
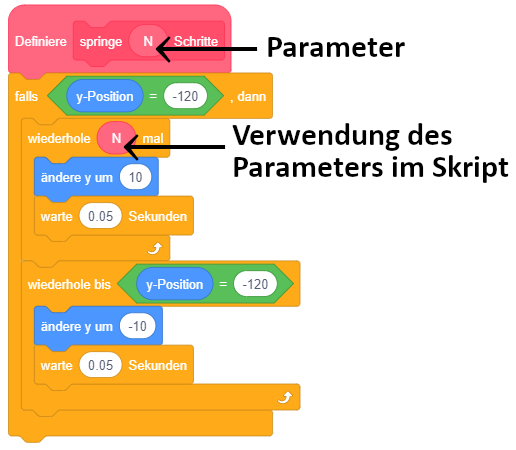
Beim Aufruf des Unterprogramms können nun – wie bereits von normalen Anweisungen bekannt – verschiedene Werte im Eingabefeld angegeben werden, die jeweils bei der Ausführung des Unterprogramms als Wert für den Parameter N verwendet werden und für unterschiedlich hohe Sprünge sorgen:

Das Verhalten von Unterprogrammen ist also durch Parameter variierbar.
Parameter sind dabei aus Sicht von Unterprogrammen lokale Variablen, denen beim Aufruf des Unterprogramms Werte zugewiesen werden. Diese Variablen können nur innerhalb des Unterprogramms verwendet werden (daher “lokal”). In Scratch können Sie außerdem – im Gegensatz zu normalen Variablen – während der Ausführung des Unterprogramms nur gelesen, aber nicht überschrieben werden.
Vorteile von Unterprogrammen
Unterprogramme eignen sich also, um Programme übersichtlich zu strukturieren und zusammengehörende Programmteile zusammenzufassen (“Modularisierung” von Programmen). Dadurch kann ein Programm in kleinere Bausteine zerlegt werden, die sich unabhängig voneinander entwickeln lassen und zu komplexeren Programmen zusammensetzen lassen.
Durch Unterprogramme lässt sich Code-Redundanz vermeiden und Programme werden besser wartbar, da nachträgliche Änderungen am Unterprogramm nur in dessen Definition durchgeführt werden müssen. Programme werden außerdem leichter testbar, indem zunächst die Unterprogramme als kleinere Einheiten getestet werden.
Ein entscheidender Vorteil ist auch die Wiederverwendbarkeit: Ein einmal entwickeltes Unterprogramm für eine bestimmte Aufgabe kann immer dann, wenn diese Aufgabe gelöst werden soll, einfach aufgerufen werden, anstatt dass der Inhalt noch einmal neu programmiert werden muss.
So erleichtern Unterprogramme auch die Zusammenarbeit, wenn viele Menschen an einem Projekt arbeiten: Hier kann zuerst überlegt werden, wie sich das Programm am besten in Unterprogramme aufteilen lässt, und anschließend werden die einzelnen Unterprogramme auf mehrere Teams verteilt und parallel entwickelt.
Nachrichten
In komplexeren Scratch-Projekten kann es nötig sein, dass ein Skript eines Objekts eine Aktion eines anderen Objekts auslösen soll. Das ist bisher nicht möglich: Wird beispielsweise ein Objekt angeklickt, kann in dem Skript, das auf dieses Ereignis reagiert, nur das Objekt selbst bewegt oder verändert werden, aber nicht ein anderes Objekt. Ebenso können Objekte in Scratch nur ihre eigenen Methoden direkt aufrufen, aber nicht Methoden von anderen Objekte (“fremder Methodenaufruf”).
Um einem Programmierobjekt mitzuteilen, dass es etwas machen soll, werden in der Programmierung Signale verwendet, die in Scratch als Nachrichten bezeichnet werden. Ein solches Signal kann mit einer speziellen Anweisung von einem Objekt ausgesendet werden und von allen Objekten empfangen werden kann (“Broadcasting”). Für Objekte kann über einen bestimmten Ereignisblock angegeben werden, auf welche Signale sie wie reagieren sollen. Nachrichten ermöglichen es also, “eigene” Ereignisse zu definieren, mittels derer verschiedene Figuren und die Bühne miteinander kommunizieren und auf einander reagieren können.
Nachrichten erstellen und versenden
Um eine Nachricht an alle Objekte zu senden, wird die Anweisung “sende Nachricht an alle” aus der Kategorie “Ereignisse” (gelb) verwendet. Die Nachricht selbst kann über die Auswahlliste ▾ ausgewählt werden. Mit der Option “Neue Nachricht” kann eine neue Nachricht erstellt werden, hier beispielsweise eine Nachricht namens “Alarm”:
Wird diese Anweisung in einem Skript ausgeführt, so wird die Nachricht “Alarm” an alle Objekte (auch an den Sender selbst) gesendet und sofort mit der nächsten Anweisung im Skript weitergemacht.
Soll das Skript dagegen warten, bis alle Objekte ihre Reaktion auf die Nachricht zuende ausgeführt haben, bevor es mit seiner nächsten Anweisung fortfährt, wird stattdessen die Anweisung “sende Nachricht an alle und warte” verwendet:
Auf Nachrichten reagieren
Um Reaktionen auf bestimmte Nachrichten zu programmieren, gibt es einen speziellen Ereignisblock in der Kategorie “Ereignisse”:

Das angehängte Skript wird ausgeführt, sobald das Objekt die angegebene Nachricht empfängt (hier die Nachricht namens “Alarm”). Ein Objekt kann dabei auch unterschiedlich auf verschiedene Nachrichten reagieren, indem Ereignisblöcke mit verschiedenen Nachrichtenbezeichnern im Skriptbereich angelegt werden:
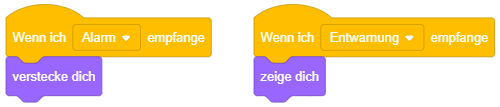
Das obenstehende Beispiel lässt ein Objekt verschwinden, wenn ein anderes Objekt die Nachricht “Alarm” sendet, und wieder erscheinen, wenn ein anderes Objekt die Nachricht “Entwarnung” sendet.
Beispiel: Kommunikation zwischen Objekten
Das folgende Beispiel demonstriert die Kommunikation zwischen mehreren Objekten anhand von Nachrichten. Sie können das Scratch-Projekt Kommunikation.sb3 hier herunterladen: Download
Hier befinden sich drei Figuren auf der Bühne (“Alice”, “Bob” und “Carol”), die Personen in einem Netzwerk darstellen. Beim Anklicken einer Figur sollen jeweils beide oder eine andere Figur reagieren.
Ein-Weg-Kommunikation
Wenn die Figur “Carol” angeklickt wird, sollen (nachdem sie eine Mitteilung angezeigt hat) Aktionen der Figuren “Alice” und “Bob” ausgelöst werden: Beide sollen ebenfalls eine Mitteilung anzeigen.
Dazu wird im Skriptbereich von “Carol” definiert, dass beim Eintreten des Ereignisses “Wenn ich angeklickt werde” eine Nachricht “stellt euch vor” gesendet wird:
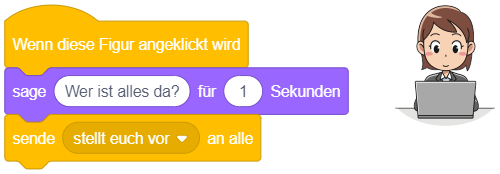
Die Reaktion der anderen beiden Figuren auf diese Nachricht wird in deren Skriptbereich mit dem Ereignisblock “wenn ich … empfange” definiert:
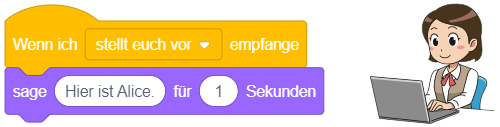
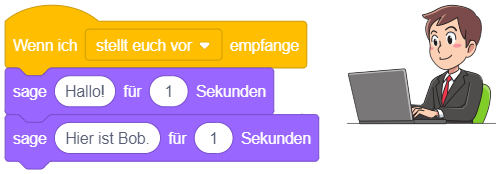
Diese Art der Kommunikation wird als “Ein-Weg-Kommunikation” bezeichnet, da das sendende Objekt kein Antwortsignal von den empfangenden Objekten erwartet. Der zeitliche Ablauf der Skriptausführung lässt sich in dem folgenden Balkendiagramm nachvollziehen:
Zwei-Wege-Kommunikation
In der “Zwei-Wege-Kommunikation” synchronisieren zwei Objekte eine Aktionssequenz, indem sie Nachrichten hin- und herschicken. In diesem Beispiel soll beim Anklicken der Figur “Alice” eine Aktion der Figur “Carol” ausgelöst werden. Wenn “Carol” ihre Aktion beendet hat, soll wiederum eine weitere Reaktion von “Alice” ausgelöst werden. Dazu werden zwei Nachrichten “prüfe Alices Aufträge” und “bedanke dich, Alice” verwendet. Der zeitliche Ablauf der Skriptausführung ist im folgenden Balkendiagramm dargestellt:
Dazu fügen wir den Figuren “Alice” und “Carol” die folgenden Skripte zur Ereignisbehandlung hinzu:
- Wird “Alice” angeklickt, sagt sie etwas und sendet die Nachricht “prüfe Alices Aufträge” (1. Aktion, Beginn der Aktionssequenz)
- Wenn “Carol”, die Nachricht “prüfe Alices Aufträge” empfängt, sagt sie etwas und sendet die Nachricht “bedanke dich, Alice” (2. Aktion)
- Wenn “Alice”, die Nachricht “bedanke dich, Alice” empfängt, sagt sie etwas (3. Aktion, Ende der Aktionssequenz)

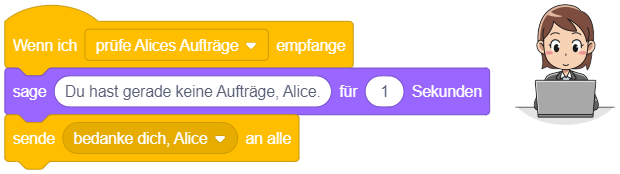
Da die Figur “Bob” keine Ereignisblöcke für diese beiden Nachrichten besitzt, reagiert sie auf diese nicht.
Analog können wir auch den Dialog zwischen “Bob” und “Carol” umsetzen (siehe Beispielvideo), indem wir weitere Nachrichten dafür verwenden (z. B. “prüfe Bobs Aufträge”, “bedanke dich, Bob”).
Kommunikation mit Warten
In Fällen wie diesen lässt sich die Zwei-Wege-Kommunikation auch vereinfachen, indem die Anweisung “sende Nachricht und warte” verwendet wird:
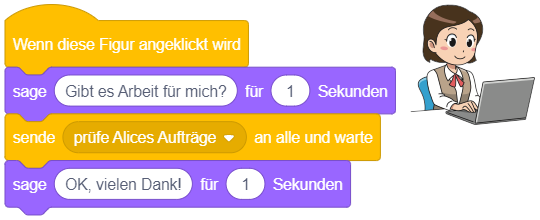
Hier pausiert das Skript des sendenden Objekts (hier “Alice”) automatisch, bis alle Objekte, die einen Ereignisblock für diese Nachricht besitzen (hier “Carol”), ihre entsprechende Reaktion zuende ausgeführt haben. In der Reaktion von “Carol” muss nun also keine Antwortnachricht mehr versendet werden:
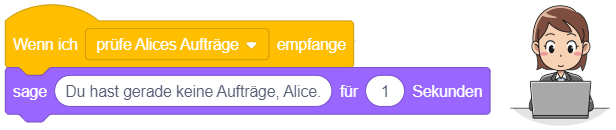
Der zeitliche Ablauf ist hier im Resultat genauso wie beim vorigen Beispiel – der Unterschied besteht darin, dass hier nur ein Skript von “Alice” ausgeführt wird (das zwischenzeitlich pausiert), statt wie im vorigen Beispiel je ein Skript für die 1. und 3. Aktion:
Anwendungsfälle für Nachrichten
Nachrichten (auch Signale) werden in der Programmierung zur ereignisgesteuerte Kommunikation zwischen Programmobjekten verwendet.
Nachrichten (“Signale”) eignen sich gut, um komplexere zeitliche Programmabläufe zu koordinieren, in denen Aktionen von Objekten durch Aktionen anderer Objekte ausgelöst werden, beispielsweise in einer Animationssequenz. Die zeitliche Abstimmung verschiedener Programmabläufe aufeinander wird als Synchronisation bezeichnet.
Mit Hilfe von Nachrichten lassen sich Objekte durch Skripte anderer Objekte steuern, beispielsweise lässt sich so eine Figur durch das Anklicken von Schaltflächen bewegen.
Nachrichten lassen sich allgemein verwenden, um selbst definierte Ereignisse eines Objekts an andere Objekte zu melden, beispielsweise “Wenn anderes Objekt angeklickt wird”, “Wenn anderes Objekt den Rand berührt” oder “Wenn anderes Objekt verschwindet/erscheint”.
Fremdmethodenaufruf
In den meisten Programmiersprachen, in denen mit Objekten gearbeitet wird, können Objekte nicht nur ihre eigenen Methoden aufrufen, sondern auch Methoden anderer Objekte (fremde Methoden). In Scratch können Nachrichten verwendet werden, um solche Fremdmethodenaufrufe umzusetzen, indem einem anderen Objekt mittels einer Nachricht mitgeteilt wird, dass es eine eigene Methode aufrufen soll.
Dazu muss für jede Methode, die durch andere Objekte aufgerufen werden kann, eine eigene Nachricht verwendet werden. Um nicht den Überblick zu verlieren, bietet es sich an, diese Nachrichten nach einem bestimmten Schema zu benennen, beispielsweise “Objekt.Methode”. Das folgende Beispiel ergänzt das Objekt “Bär” aus dem Beispiel zu Unterprogramme um das entsprechende Ereignis:
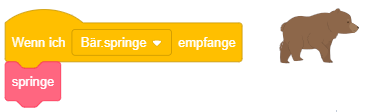
Die Methode “springe” dieses Objekts kann nun durch andere Objekte mit der Anweisung “sende Bär.springe an alle” aufgerufen werden (bzw. “sende … und warte”, wenn das aufrufende Skript erst nach dem Fremdmethodenaufruf fortfahren soll):
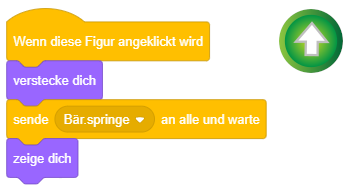
-
zur Erinnerung: siehe Lektion 1 – Einstieg in Scratch, Abschnitt Parameter und Werte ↩︎
-
Neben Eingabefeldern für Parameter können in Scratch auch weitere Textteile zum Namen des neuen Blocks hinzugefügt werden, um ihn in natürlicher Sprache lesbarer zu machen oder für die programmierenden Menschen hilfreiche Informationen zu den Parametern zu ergänzen (z. B. Einheiten). In diesem Beispiel heißt der Block “springe (N) Schritte”, wobei (N) ein Eingabefeld für einen Parameter darstellt, der im Unterprogramm-Skript “N” heißt. ↩︎
1.5.1 Übungsaufgaben
Praktische Übungen
Aufgabe 1: Parametrisierte Unterprogramme
Aufgaben zum Zeichnen geometrischer Formen eignen sich gut, um die Verwendung von Unterprogrammen zu motivieren: Anweisungssequenzen zum Zeichnen einfacher geometrischer Formen können als Unterprogramme definiert werden und anschließend zum Zeichnen komplexerer Formen verwendet werden.
In dieser Aufgabe soll ein Unterprogramm zum Zeichnen von Kreisen definiert werden und zum Zeichnen einer aus Kreisen zusammengesetzten Form verwendet werden. Laden Sie zunächst die Projektdatei Kreise_zeichnen.sb3 herunter und öffnen Sie sie in Scratch: Download
Das Programm enthält als Vorlage eine Anweisungssequenz, mittels der ein Kreis mit einem Radius von 80 Pixeln um den Mittelpunkt x = 0, y = 0 gezeichnet wird:1
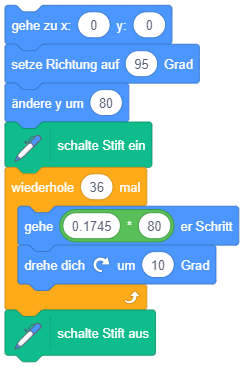
Definieren Sie ein Unterprogramm “zeichne Kreis” mit geeigneten Parametern, das einen Kreis mit beliebigem Radius um einen beliebigen Mittelpunkt zeichnet. Als Grundlage für das Unterprogramm können Sie das vorhandene Skript verwenden.
Verwenden Sie das Unterprogramm dann, um beim Programmstart den Buchstaben “Ö” zu zeichnen. Der Buchstabe besteht aus vier Kreisen wie hier dargestellt:
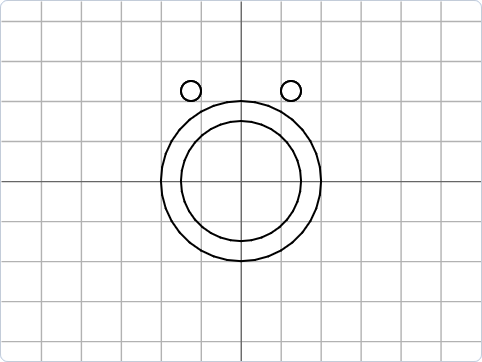 |
Äußerer Kreis: Mittelpunkt (0, 0), Radius 80 Pixel Innerer Kreis: Mittelpunkt (0, 0), Radius 60 Pixel Linker Punkt: Mittelpunkt (-50, 90), Radius 10 Pixel Rechter Punkt: Mittelpunkt (50, 90), Radius 10 Pixel |
Aufgabe 2: Synchronisation mittels Nachrichten
In den Übungsaufgaben zu Lektion 1 wurde eine Animationssequenz entwickelt, indem die Aktionen der einzelnen Figuren mittels “warte”-Anweisungen zeitlich aufeinander abgestimmt wurden (siehe Aufgabe Animationssequenz nach Drehbuch erstellen). Diese Vorgehensweise ist relativ unflexibel: Wenn wir die Aktionen eines Objekts nachträglich ändern möchten und sich dadurch deren Dauer ändert, müssen wir die “warte”-Anweisungen für alle folgenden Aktionen in allen Skripten der anderen Objekte anpassen. Nachrichten bieten eine flexiblere Möglichkeit, den zeitlichen Ablauf von Aktionen verschiedener Objekte zu koordinieren (d. h. die Abläufe zu synchronisieren).
In dieser Aufgabe soll eine Animationssequenz mit Hilfe von Nachrichten umstrukturiert werden. Laden Sie zunächst die Projektdatei Knock_Knock.sb3 herunter und öffnen Sie sie in Scratch: Download
Überprüfen Sie die Skripte der beiden Figuren. Die Skripte verwenden “warte”-Anweisungen, um beim Programmstart eine aufeinander abgestimmte Animations- und Dialogsequenz abzuspielen.
Ändern Sie das Programm so, dass die Aktionen der Figuren mit Hilfe von Nachrichten synchronisiert werden. Das folgende Diagramm zeigt skizzenhaft, in welcher Reihenfolge die Nachrichten nach dem Programmstart zwischen den Objekten ausgetauscht werden und welche Aktionen jeweils ausgelöst werden:2
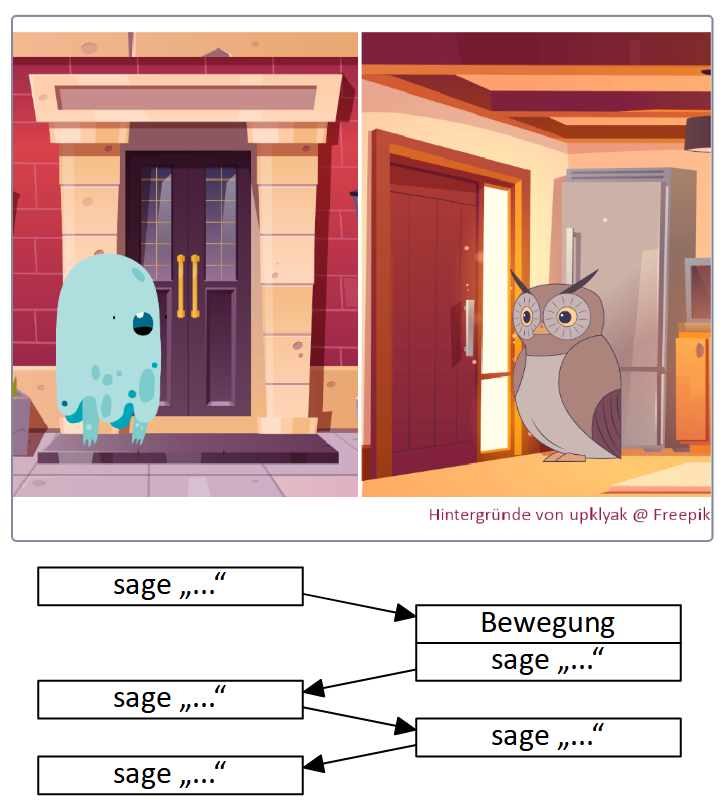
Aufgabe 3: Steuerung mittels Nachrichten
Laden Sie die Projektdatei Baseball.sb3 als Vorlage herunter: Download
Das Projekt enthält eine Figur “Ball”, deren Richtung mit den Pfeiltasten nach oben und unten gedreht werden kann. Beim Drücken der Leertaste führt die Figur “Spielerin” eine Schlaganimation aus und der Ball fliegt entlang seiner eingestellten Richtung zum Bildschirmrand. Danach erscheint er wieder an seiner Ausgangsposition.
Das Programm soll nun so umgeschrieben werden, dass die Figuren durch Anklicken der drei Schaltflächen oben links gesteuert werden, statt über die Tastatur.
Richtung einstellen
Durch Anklicken der beiden Schaltflächen und soll die Richtung des Balls geändert werden, statt durch Drücken der Pfeiltasten.
Ball schlagen
Beim Anklicken der Schaltfläche der mittleren Schaltfläche soll die Schlaganimation der Spielerin und die Bewegung des Balls ausgelöst werden, statt durch Drücken der Leertaste.
Schaltflächen deaktivieren
Sobald der Schlag durch die mittlere Schaltfläche ausgelöst wurde, sollen alle drei Schaltflächen verschwinden, bis der Ball den Bildschirmrand erreicht hat und sich wieder an seiner Ausgangsposition befindet.
Aufgabe 4: Programm umstrukturieren
In dieser Aufgabe soll die Anwendung zur 2D-Transformation aus der vorigen Übung überarbeitet werden.
Laden Sie die dazu Projektdatei 2D-Transformation_mit_Test.sb3 herunter: Download
Momentan wird beim Drücken der Leertaste geprüft, ob die Form der roten Figur mit der grünen Zielfigur übereinstimmt. Strukturieren Sie das Programm mit Hilfe von Unterprogrammen und Nachrichten folgendermaßen um:
- Die Überprüfung soll nun nach jeder Eingabe für die rote Figur (also Bewegung, Drehung oder Größenänderung) automatisch durchgeführt werden. Die Leertaste wird also nicht mehr benötigt. Dabei sollen keine Code-Duplikate im Skript vorkommen.
- Falls die Form der roten Figur mit der Zielfigur übereinstimmt, nimmt die Zielfigur eine neue zufällige Transformation ein. Anderenfalls passiert nichts (die Mitteilungen “Die Position/Größe/Richtung stimmt nicht.” können also gelöscht werden). Auch hier sollen Code-Duplikate im Skript vermieden werden.
-
Der Kreis wird hier, wie in der Computergrafik üblich, durch ein regelmäßiges Vieleck approximiert – in diesem Fall durch ein 36-Eck. Da für einen Kreis mit dem Radius r der Umfang 2·π·r beträgt, ist jede Seite des 36-Ecks hier π/18·r lang (also ungefähr 0.1745·r). ↩︎
-
Das Bild wurde erstellt unter Verwendung von Hintergründen von Upklyak @ Freepik. ↩︎
1.5.2 Vertiefung
Klonen von Objekten
In der Lektion zu Variablen wurde das Spiel Fische fangen entwickelt, in dem mehrere Kopien eines Objekts sich unabhängig voneinander über die Bühne bewegen und per Mausklick gefangen werden können. Dazu haben wir zwei Duplikate des Objekts “Fisch1” erstellt.
Dieses Vorgehen hat allerdings mehrere Nachteile, die zu Programmierfehlern führen können:
- Sobald viele Kopien eines Objekts benötigt werden, geht schnell der Überblick verloren. Außerdem muss von vornherein bekannt sein, wie viele Kopien des Objekts benötigt werden. Manchmal entscheidet sich das allerdings erst zur Laufzeit.
- Wenn nachträglich eine Änderung in einem Skript der Figur vorgenommen werden soll, muss das Skript jeder Kopie der Figur angepasst werden, was zeitaufwendig und fehleranfällig ist. Auch in diesem Fall haben wir es also mit Code-Redundanz zu tun.
Eine bessere Lösung besteht darin, erst zur Laufzeit des Programms temporäre Kopien eines Objekts erstellen zu lassen, die nach Programmende automatisch gelöscht werden.
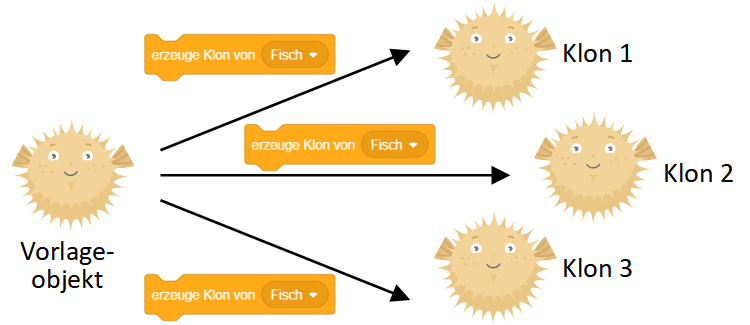
Solche temporären Objektkopien werden in Scratch als “Klone” bezeichnet und können durch bestimmte Anweisungen verwaltet werden.
Erzeugen und Löschen von Klonen
In Scratch gibt es je eine Anweisung zum Erzeugen und zum Löschen von Klonen eines Objekts, die sich in der Kategorie “Steuerung” (orange) befinden:
 |
Erzeugt einen Klon des angegebenen Objekts oder des Objekts selbst, welches das Skript ausführt. |
 |
Löscht das Objekt, zu dem das Skript gehört, sofern es als Klon entstanden ist. Anderenfalls hat diese Anweisung keinen Effekt. |
Ein Klon ist eine exakte Kopie des Objekts, aus dem es entstanden ist. Es hat also die gleichen Attribute, Objektvariablen, Grafiken und Soundeffekte. Sein Zustand – also die Werte seiner Attribute – entspricht dem Zustand des Ursprungsobjekts zu dem Zeitpunkt, zu dem die Anweisung “Erzeuge Klon” ausgeführt wird. Ab diesem Zeitpunkt ist es aber komplett unabhängig von dem Objekt, aus dem es entstanden ist.
Beim Beenden des Programms durch Klicken auf das Stop-Symbol  werden automatisch alle vorhandenen Klone gelöscht – also alle Objekt, die durch Anweisungen “Erzeuge Klon” entstanden sind.
werden automatisch alle vorhandenen Klone gelöscht – also alle Objekt, die durch Anweisungen “Erzeuge Klon” entstanden sind.
Initialisieren von Klonen
Damit ein Klon bestimmte Aktionen durchführen kann, wenn er entsteht, bietet Scratch einen Ereignisblock in der Kategorie “Steuerung” (orange) an:
 |
Das angehängte Skript wird ausgeführt, sobald ein Klon dieses Objekts entsteht. Das Skript wird dabei für den erzeugten Klon und nicht für das Objekt, das als Vorlage für den Klon dient, ausgeführt. |
Dieses Ereignis dient dazu, ein neu als Klon entstandenes Objekt zu initialisieren, also seinen Anfangszustand festzulegen, beispielsweise seine Sichtbarkeit oder Position. Oft bietet es sich an, bei der Initialisierung bestimmte Attribute auf Zufallswerte zu setzen, um das Verhalten der Klone zu variieren.
Beispiel: Fische fangen
Im folgenden Beispiel überarbeiten wir das Spiel Fische fangen so, dass mit Klonen statt mit “echten” Duplikaten von Objekten gearbeitet wird. Dazu entfernen wir die beiden Duplikate der Figur “Fisch” und passen das Skript der Figur folgendermaßen an:
- Das Skript zur Initialisierung und dauerhaften Bewegung des Objekts wird ausgeführt, wenn das Objekt als Klon entsteht, nicht beim Programmstart. (1.)
- Falls beim Anklicken die Trefferzahl den Wert 0 erreicht, kann der Klon wieder gelöscht werden, um nicht unnötig Speicherplatz und Rechenzeit der Scratch-Entwicklungsumgebung zu verbrauchen. (2.)
- Beim Löschen des Klons werde alle ggf. noch laufenden Skript von ihm abgebrochen. Diese Endloswiederholung bricht also ab, sobald der Klon das dritte Mal angeklickt wurde. (3.)
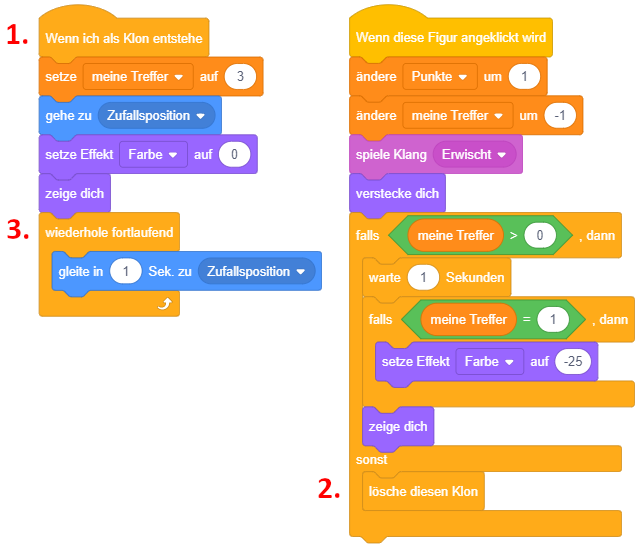
Die Figur “Fisch” selbst setzen wir über das Attributfenster über der Objektliste manuell auf “unsichtbar”. Diese Figur bleibt nun auch unsichtbar, da sie nur noch als Vorlage für die Klone dient und selbst im Spiel gar nicht mehr vorkommt.
Als Nächstes müssen die Klone noch erzeugt werden. Dazu wird im Startskript der Bühne eine Wiederholung ergänzt, die drei Klone der Figur “Fisch” erstellt:
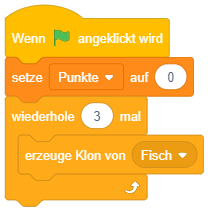
Ein weiterer Vorteil der Verwendung von Klonen ist, dass die Anzahl der Objekte nicht von vornherein festgelegt ist. Statt eine feste Anzahl von Fischen zu erstellen, könnte das Skript der Bühne beispielsweise auch in Endloslosschleife im Hintergrund alle drei Sekunden neue Fische generieren:
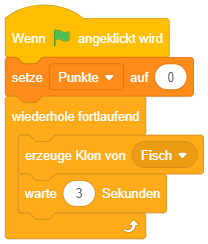
Das Scratch-Projekt zu diesem Beispiel können Sie hier herunterladen: Download
Das Objekt, das geklont wird, dient oft nur noch als Objektvorlage für die Klone und kommt im Programm selbst nicht mehr vor – dazu wird seine Sichtbarkeit auf “unsichtbar” gesetzt. Da die Klone damit initial ebenfalls unsichtbar sind, müssen sie in diesem Fall in ihrem Initialisierungsskript ihre Sichtbarkeit auf “sichtbar” ändern:
Partikelsysteme
Ein typisches Beispiel für die Verwendung von Objektklonen stellen Partikelsysteme dar – also Animationen, in denen eine größere Anzahl von gleichartigen Objekten (“Partikel”) animiert wird. Solche Partikelsysteme können etwa zur Simulation von Feuer-, Rauch- oder Explosionseffekten oder für Wettereffekte wie Regen oder Schnee verwendet werden. Hier werden beispielsweise alle Regentropfen oder Schneeflocken durch Objektklone dargestellt, die sich alle gleich oder ähnlich (mit leichten, meist zufällig gewählten Variationen) verhalten und aussehen.
Das folgende Beispiel demonstriert ein einfaches Partikelsystem zur Darstellung von Regentropfen. Hier gibt es ein einzelnes Objekt “Partikel”, dessen Grafik einen Regentropfen darstellt. Dieses Objekt dient als Objektvorlage für die Regentropfen, die zur Laufzeit erzeugt werden, und wird selbst auf unsichtbar gesetzt.
Beim Klonen des Objekts wird das folgende Skript für den Klon ausführt:
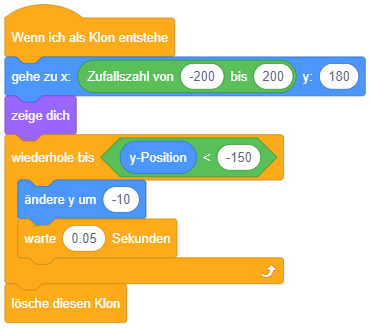
Dieses Skript legt die Startposition des neuen Partikels fest und lässt es auf der Bühne erscheinen. Die x-Koordinate wird dabei für jedes Partikel unabhängig voneinander zufällig gewählt. Anschließend bewegt es sich abwärts, bis es den Boden erreicht und gelöscht werden kann.
Um die Partikel zu variieren, könnten weitere Attribute zu Beginn dieses Skript zufällig festgelegt werden (z. B. ein Zufallswert zwischen 50% und 100% für die Größe).
In diesem Beispiel sollen nach dem Starten des Programms fortwährend neue Partikel erzeugt werden (hier: 5 Partikel pro Sekunde). Dazu wird zur Bühne ein entsprechendes Skript hinzugefügt:
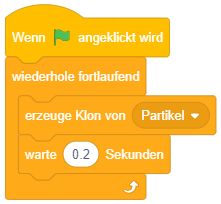
Das Scratch-Projekt zu diesem Beispiel können Sie hier herunterladen: Download
Praktische Übungen
Aufgabe: Partikelsystem mit Klonen
In dieser Aufgabe soll ein einfaches Partikelsystem in Scratch umgesetzt werden, in dem die einzelnen Partikel durch Klone einer Objektvorlage realisiert werden. Laden Sie dazu die Projektdatei Partikelsystem.sb3 herunter: Download
Auf der Bühne befindet sich eine Rakete, die mit den Pfeiltasten nach links und rechts gedreht werden kann (siehe Skript im Objekt “Rakete”), sowie ein Objekt “Partikel”, das ein einzelnes Funkenpartikel darstellt. Ziel ist es nun, einen Funkenschweif zur Rakete hinzuzufügen.
Partikel erzeugen und bewegen
Als Erstes sollen Funken automatisch erzeugt und animiert werden. Dabei dient das Objekt “Partikel” als Objektvorlage für die Partikelklone.
- Die Rakete soll alle 50 ms einen neuen Funken erzeugen. Die initiale Posion der Funken ist also die aktuelle Position der Rakete.
- Sobald ein Funke entsteht, bewegt er sich in einer geraden Linie in entgegengesetzter Richtung von der Rakete weg (z. B. in 10-er Schritten alle 50 ms).
- Wenn ein Funke den Bildschirmrand berührt, verschwindet er von der Spielfläche und kann gelöscht werden.
Partikelverhalten variieren
Sorgen Sie nun dafür, dass nicht alle Partikel gleich aussehen und sich gleich verhalten, sondern leichte zufallsbedingte Variationen aufweisen:
- Die Größe der Partikel kann zwischen 50% bis 100% der Objektvorlage variieren.
- Die Bewegungsrichtung kann bis zu 10° von der entgegengesetzten Richtung der Rakete abweichen.
- Jedes Partikel hat eine eigene Geschwindigkeit, die zwischen 10 bis 20 Pixel pro 50 ms betragen kann.
Für die letzte Anforderung kann es hilfreich sein, die Geschwindigkeit der einzelnen Partikel als Objektvariable zu speichern. Zur Erinnerung: Jeder Klon hat seine eigene Version der Objektvariablen seiner Vorlage.
Aufgabe: Nachrichten und Objektklone
In dieser Aufgabe wird das Aufrufen von Skripten anderer Objekte mittels Nachrichten, sowie das Arbeiten mit Objektklonen behandelt. Laden Sie zunächst die Projektdatei Windrad.sb3 herunter: Download
Das Projekt enthält eine Figur “Windrad”, die beim Starten des Programms dem Mauszeiger folgt und per Mausklick eine Wirbelanimation ausführt. Außerdem befindet sich ein Objekt “Ball” auf der Bühne, der beim Programmstart an einer zufälligen Position erscheint.
Skript eines anderen Objekts aufrufen
Passen Sie das Programm so an, dass der Ball mittels einer Nachricht informiert wird, wenn das Windrad seine Wirbelanimation ausführt. Beträgt der Abstand vom Ball zum Windrad weniger als 150 Pixel, so soll er sich in einer geraden Linie vom Windrad wegbewegen, bis er den Bildschirmrand berührt.
Um den Ball zum Windrad hinzudrehen, kann der Block “drehe dich zu …” verwendet werden:
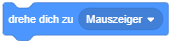
Objektklone erstellen
Machen Sie den Ball nun unsichtbar und passen Sie das Programm so an, dass zu Beginn 10 Klone des Balls zufällig auf der Bühne verteilt werden. Das Objekt “Ball” selbst dient jetzt nur noch als Vorlage für die Klone.
Wenn ein Klon den Bildschirmrand berührt, soll er nun verschwinden (“lösche diesen Klon”). Außerdem soll die Bühne nach Programmstart jede Sekunde einen neuen Klon erzeugen, der zufällig auf der Bühne positioniert wird.
1.6 Anhang
1.6.1 Scratch-Referenz
Blöcke in Scratch
| Blocktypen | ||
|---|---|---|
 |
“Stapelblockform” | Anweisung |
 |
“Klammerblockform” | Kontrollstruktur (z. B. eine Fallunterscheidung oder Wiederholung), siehe Steuerung |
 |
“Kopfblockform”, gewölbt | Ereignisbehandlung (Beginn eines Skripts, das beim Eintreten des Ereignisses ausgeführt wird), siehe Ereignisse |
 |
“Kopfblockform”, flach | Methodendefinition (Beginn eines Skripts, das durch einen speziellen Anweisungsblock ausgeführt wird), siehe Meine Blöcke |
 |
“Werteblockform” | Wert (eine Zahl oder Zeichenkette, z. B. der Wert eines Attributs, einer Variablen oder eines Berechnungsergebnisses) |
 |
“Wahrheitswerteblockform” | Wahrheitswert (wahr oder falsch, wird z. B. für Bedingungen in anderen Blöcken verwendet) |
Bewegung
| Anweisungen | |
|---|---|
 |
Versetzt die Position des Objekts um die angegebene Distanz entlang seiner Richtung. |
 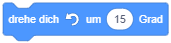 |
Ändert die Richtung des Objekts um den angegebenen Wert im oder gegen der Uhrzeigersinn (Winkel in Grad). |
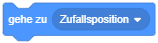 |
Setzt die Position des Objekts auf das ausgewählte Ziel: zufällig ausgewählte Koordinaten auf der Bühne, die aktuelle Position des Mauszeigers oder die Koordinaten eines anderen Objekts. Das Ziel kann über das Symbol ▾ festgelegt werden. |
 |
Setzt die Position des Objekts auf die angegebenen Koordinaten. |
 |
Bewegt das Objekt in der angegebenen Zeitspanne kontinuierlich zum ausgewählten Ziel (Zufallskoordinaten oder anderes Objekt).1 |
 |
Bewegt das Objekt in der angegebenen Zeitspanne kontinuierlich zu den angegebenen Koordinaten.1 |
 |
Setzt die Richtung auf den angegebenen Wert (Winkel in Grad). |
 |
Dreht das Objekt in Richtung des ausgewählten Ziels. |
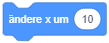  |
Addiert den angegebenen Wert zur x- oder y-Koordinate des Objekts. |
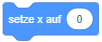 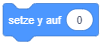 |
Setzt die x- oder y-Koordinate des Objekts auf den angegebenen Wert. |
 |
Falls das Objekt den Rand der Bühne überschneidet, wird es vom Rand weg in die Bühne versetzt und ggf. gedreht, so dass es den Rand gerade noch berührt. Anderenfalls hat die Anweisung keinen Effekt. |
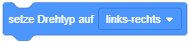 |
Legt den Drehtyp fest, d. h. wie die Richtung des Objekts seine Darstellung beeinflusst: rotiert um den Richtungswinkel, gespiegelt bei negativem Richtungswinkel oder keine Änderung. |
| Werte | |
|---|---|
  |
Gibt als Wert die momentane x- oder y-Koordinate des Objekts an. |
 |
Gibt als Wert die momentane Richtung des Objekts an (Winkel in Grad). |
Aussehen
| Anweisungen | |
|---|---|
  |
Zeigt den angegebenen Text am Objekt in einer Sprech- oder Denkblase an. |
 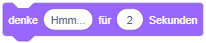 |
Zeigt den angegebenen Text für die angegebene Zeitspanne an.1 |
  |
Legt die angegebene Grafik für das Objekts fest oder wechselt zur nächsten Grafik. |
  |
Legt das angegebene Hintergrundbild für die Bühne fest oder wechselt zum nächsten Bild. Löst das Ereignis “Bühnenbild wechselt zu Bild” aus. |
 |
Addiert den angegebenen Wert zur Größe des Objekts (in Prozent). |
 |
Setzt die Größe des Objekts auf den angegebenen Wert (in Prozent). |
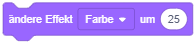 |
Addiert den angegebenen Wert zum ausgewählten Grafikeffekt des Objekts. Es gibt Grafikeffekte zum Ändern des Farbton, der Helligkeit und Transparenz, sowie zum Verzerren (Fischauge, Wirbel), Verpixeln (Pixel) und Vervielfältigen (Mosaik) der Grafik.2 |
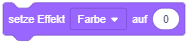 |
Setzt den ausgewählten Grafikeffekt des Objekts auf den angegebenen Wert. |
 |
Setzt alle Grafikeffekte des Objekts auf den Normalzustand zurück. |
  |
Macht das Objekt unsichtbar oder macht es wieder sichtbar.3 |
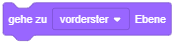 |
Setzt das Objekt auf die vorderste oder hinterste Ebene (Auswahl über das Symbol ▾). Die Objekte werden nach Ebenen sortiert auf der Bühne gezeichnet, so dass Objekte andere Objekte überdecken, die weiter hinten liegen. |
 |
Schiebt das Objekt im Ebenenstapel um die angegebene Anzahl von Ebenen nach vorne oder hinten. |
| Werte | |
|---|---|
 |
Gibt als Wert die Nummer oder den Namen der aktuellen Grafik des Objekts an (Wahl zwischen Nummer oder Name über das Symbol ▾). |
 |
Gibt als Wert die Nummer oder den Namen des aktuellen Hintergrundbilds des Bühne an. |
 |
Gibt als Wert die momentane Größe des Objekts an (in Prozent). |
Klang
| Anweisungen | |
|---|---|
 |
Startet den angegebenen Sound des Objekt und spielt ihn im Hintergrund ab. |
 |
Startet den angegebenen Sound des Objekts und wartet, bis der Sound zuende abgespielt wurde.1 |
 |
Bricht alle momentan laufenden Sounds des Objekt ab. |
 |
Addiert den angegebenen Wert zum ausgewählten Wiedergabeeffekt des Objekts: Tonhöhe oder Stereo-Aussteuerung (links/rechts).4 |
 |
Setzt den ausgewählten Wiedergabeeffekt des Objekts auf den angegebenen Wert. |
 |
Setzt alle Wiedergabeeffekte des Objekts auf den Normalzustand zurück. |
 |
Addiert den angegebenen Wert zur Lautstärke für die Sound-Ausgabe des Objekts (in Prozent). |
 |
Setzt die Lautstärke für die Sound-Ausgabe des Objekts auf den angegebenen Wert (in Prozent). |
| Werte | |
|---|---|
 |
Gibt als Wert die momentane Lautstärke für die Sound-Ausgabe des Objekts an (in Prozent). |
Ereignisse
| Ereignisse | |
|---|---|
 |
Das angehängte Skript wird beim Klicken auf die grüne Fahne  ausgeführt. ausgeführt. |
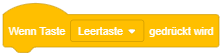 |
Das angehängte Skript wird beim Drücken der ausgewählten Taste ausgeführt (Auswahl der Taste über das Symbol ▾). |
 |
Das angehängte Skript wird ausgeführt, sobald das Objekt mit der Maus angeklickt wird. |
 |
Das angehängte Skript wird ausgeführt, sobald das Bühnenbild zum ausgewählten Bild wechselt (Auswahl des Bildnamen über das Symbol ▾), z. B. weil in einem anderen Skript die Anweisung “wechsle zu Bühnenbild …” ausgeführt wird. |
 |
Das angehängte Skript wird ausgeführt, sobald die momentan über das Mikrofon gemessene Lautstärke den angegebenen Wert (0 bis 100) überschreitet. |
 |
Das angehängte Skript wird ausgeführt, sobald der Wert der Stoppuhr den angegebenen Wert (in Sekunden) überschreitet.5 Dazu muss im vorigen Block in der Auswahlliste über das Symbol ▾ der Messwert “Stoppuhr” statt “Lautstärke” ausgewählt werden. |
Nachrichten
| Ereignisse | |
|---|---|
 |
Das angehängte Skript wird ausgeführt, sobald das Objekt die ausgewählte Nachricht empfängt (Auswahl der Nachricht über das Symbol ▾).6 |
| Anweisungen | |
|---|---|
 |
Verschickt die ausgewählte Nachricht an alle Objekte (auch an sich selbst). |
 |
Verschickt die ausgewählte Nachricht und wartet anschließend, bis alle Objekte, die auf diese Nachricht reagieren, das Ereignis verarbeitet haben.7 |
Steuerung
| Kontrollstrukturen | |
|---|---|
 |
Führt die enthaltenen Blöcke wiederholt nacheinander aus, bis das Programm abgebrochen wird (endlose Wiederholung). |
 |
Führt die enthaltenen Blöcke n-mal nacheinander aus, wobei n die angegebene Zahl ist (Wiederholung mit fester Anzahl). |
 |
Führt die enthaltenen Blöcke wiederholt nacheinander aus, bis die angegebene Bedingung erfüllt ist (bedingte Wiederholung). |
 |
Führt die Blöcke in der Klammer nur dann aus, falls die angegebene Bedingung erfüllt ist (bedingte Anweisung). |
 |
Führt die Blöcke in der oberen Hälfte nur dann aus, falls die angegebene Bedingung erfüllt ist. Anderenfalls werden die Blöcke in der unteren Hälfte ausgeführt (bedingte Anweisung mit Alternative, Fallunterscheidung). |
| Anweisungen | |
|---|---|
 |
Pausiert das Skript für die angegebene Zeitspanne.1 |
 |
Pausiert das Skript, bis die angegebene Bedingung erfüllt ist. |
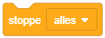 |
Bricht entweder das Skript selbst, alle anderen momentan laufenden Skripte des Objekts oder alle Skripte ab (Auswahl über das Symbol ▾).8 |
Objekte klonen
| Ereignisse | |
|---|---|
 |
Das angehängte Skript wird ausgeführt, sobald ein Klon dieses Objekts entsteht. Das Skript wird dabei für den erzeugten Klon und nicht für das Objekt, das den Klon erzeugt, ausgeführt. |
| Anweisungen | |
|---|---|
 |
Erzeugt einen Klon des ausgewählten Objekts, also ein neues Objekt, das die gleichen Attributwerte wie das Vorlageobjekt hat und Kopien aller Skripte und Ressourcen dieses Objekts enthält.9 |
 |
Löscht das Objekt, sofern es als Klon entstanden ist. Für ein originales Objekt hat die Anweisung keinen Effekt.10 |
Fühlen
| Anweisungen | |
|---|---|
 |
Zeigt den angegebenen Text am Objekt in einer Sprechblase an und pausiert das Skript dann, bis eine Antwort über die Tastatur eingegeben und die Eingabetaste gedrückt wurde. Die Antwort befindet sich anschließend im “Antwort”-Werteblock:  |
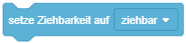 |
Legt fest, ob ein Objekt auch im Präsentationsmodus mit der Maus verschoben werden kann. Im Entwurfsmodus sind Objekte immer mit der Maus ziehbar. |
| Werte | |
|---|---|
 |
Gibt den Wert an, der als Antwort auf die zuletzt gestellte Frage eingegeben wurde. |
 |
Gibt als Wahrheitswert an, ob das Objekt gerade den Mauszeiger, den Bühnenrand oder ein bestimmtes anderes Objekt berührt (Auswahl des Ziels über das Symbol ▾).3 |
 |
Gibt als Wahrheitswert an, ob das Objekt gerade einen Bildschirmpunkt mit der angegebenen Farbe berührt. |
 |
Gibt als Wahrheitswert an, ob ein Punkt des Objekts, der die erste angegebene Farbe hat, einen Bildschirmpunkt berührt, der die zweite angegebene Farbe hat. |
 |
Gibt als Wert den Abstand des Objekts zum Mauszeiger oder zu einem anderen Objekt an (Auswahl des Ziels über das Symbol ▾). |
 |
Gibt als Wahrheitswert an, ob momentan die ausgewählte Taste gedrückt ist (Auswahl der Taste über das Symbol ▾). |
 |
Gibt als Wahrheitswert an, ob momentan eine Maustaste gedrückt ist. |
  |
Gibt als Wert die x- oder y-Koordinate des Mauszeigers an. |
  |
Gibt den Wert eines beliebigen Attributs/einer Objektvariable eines anderen Objekts oder der Bühne an. Über die linke Auswahlliste (Symbol ▾) kann das gewünschte Attribut (z. B. x-/y-Koordinate oder Richtung) und über die rechte Auswahlliste das Objekt oder die Bühne ausgewählt werden.11 |
 |
Gibt als Wert die Lautstärke an, die momentan über das Mikrofon gemessen wird (0 bis 100). |
 |
Gibt als Wert Ihren Benutzernamen an (nur in der Online-Version von Scratch, sofern Sie mit Ihrem Account eingeloggt sind, ergibt sonst eine leere Zeichenkette). |
Zeitmessung
| Anweisungen | |
|---|---|
 |
Setzt die globale Zeitmessung (“Stoppuhr”) auf 0 zurück.5 |
| Werte | |
|---|---|
 |
Gibt als Wert den aktuellen Stand der Stoppuhr an (in Sekunden).5 |
 |
Gibt als Wert einen Teil der aktuellen Zeit an. Über die Auswahlliste (Symbol ▾) kann festgelegt werden, ob die Sekunden, Minuten, Stunden, der Wochentag, Monatstag, Monat oder die Jahreszahl der aktuellen Zeit ermittelt werden sollen. |
 |
Gibt als Wert die Tage an, die seit dem 1.1.2000 vergangen sind (als Dezimalzahl, z. B. 7500.25 für 7500 Tage und 6 Stunden). |
Operatoren
| Werte | |
|---|---|
    |
Gibt als Wert das Berechnungsergebnis für die beiden enthaltenen Werte an (Addition, Subtraktion, Multiplikation oder Division). |
 |
Gibt als Wert den Teilungsrest der ganzzahligen Division von a durch b an, wobei a und b die beiden enthaltenen Werte sind (Modulo-Operator). |
 |
Gibt als Wert den enthaltenen Wert gerundet auf die nächste Ganzzahl an. |
 |
Gibt als Wert das Berechnungsergebnis für den enthaltenen Wert an, wobei verschiedene Funktionen ausgewählt werden können (über das Symbol ▾), u. a.: Betrag, ab-/aufrunden, Wurzel, Sinus, Kosinus, Tangens, Logarithmus und Exponentialfunktion. |
 |
Gibt als Wert eine zufällig ausgewählte Ganzzahl zwischen a und b an, wobei a und b die beiden enthaltenen Zahlen sind. Wenn a und b Ganzzahlen sind, wird eine Ganzzahl ausgewählt, sonst eine Dezimalzahl. |
   |
Gibt als Wahrheitswert an, ob der Vergleich der beiden enthaltenen Werte stimmt oder nicht (größer als, kleiner als, gleich). |
Wahrheitswerte
| Werte | |
|---|---|
 |
Gibt als Wahrheitswert an, ob beide enthaltenen Bedingungen erfüllt sind (logische Konjunktion). |
 |
Gibt als Wahrheitswert an, ob mindestens eine der beiden enthaltenen Bedingungen erfüllt ist (logische Disjunktion). |
 |
Gibt als Wahrheitswert an, ob die enthaltene Bedingung nicht erfüllt ist (logische Negation). |
Zeichenketten
| Werte | |
|---|---|
 |
Gibt als Wert die Verknüpfung (Konkatenation) der beiden enthaltenen Zeichenketten-Werte an. |
 |
Gibt als Wert das n-te Zeichen der angegebenen Zeichenkette an, wobei n die im linken Feld angegebene Zahl ist. |
 |
Gibt als Wert die Länge der angegebenen Zeichenkette an (d. h. die Anzahl ihrer Zeichen). |
 |
Gibt als Wahrheitswert an, ob die links angegebene Zeichenkette die rechts angegebene Zeichenkette enthält. Groß- und Kleinschreibung spielt dabei keine Rolle (“Apfel” enthält also sowohl “a” als auch “PF”). |
Variablen
| Anweisungen | |
|---|---|
 |
Setzt die ausgewählte Variable auf den angegebenen Wert (Auswahl der Variablen über das Symbol ▾).12 |
 |
Addiert den angegebenen Wert zum aktuellen Wert der ausgewählte Variablen. |
 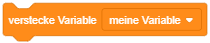 |
Zeigt den aktuellen Wert der ausgewählten Variablen live auf der Bühne an oder entfernt die Anzeige wieder. |
| Werte | |
|---|---|
 |
Gibt den momentanen Wert dieser Variablen an. |
Listen
| Anweisungen | |
|---|---|
 |
Hängt den angegebenen Wert als neues Element an die ausgewählte Liste an (Auswahl der Liste über das Symbol ▾).13 |
 |
Löscht das Element an der angegebenen Position aus der ausgewählten Liste. |
 |
Löscht alle Elemente aus der ausgewählten Liste. |
 |
Fügt den angegebenen Wert als neues Element an der angegebenen Position in die ausgewählte Liste ein. Alle ab dieser Position vorhandenden Elemente werden um eine Position nach rechts verschoben. |
 |
Überschreibt das Element an der angegebenen Position durch den angegebenen Wert. |
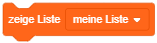  |
Zeigt den aktuellen Inhalt der ausgewählten Liste live auf der Bühne an oder entfernt die Anzeige wieder. |
| Werte | |
|---|---|
 |
Gibt als Wert das Element an der angegebenen Position in der ausgewählten Liste an. |
 |
Gibt als Wert die Position des angegebenen Wertes in der ausgewählten Liste an. Wenn der angegebene Wert mehrmals in der Liste vorkommt, wird die Position des ersten Vorkommens ermittelt. |
 |
Gibt als Wert die Länge der ausgewählten Liste an (d. h. die Anzahl ihrer Elemente). |
 |
Gibt als Wahrheitswert an, ob die ausgewählte Liste den angegebenen Wert (mindestens einmal) enthält. |
 |
Gibt als Wert den momentanen Inhalt dieser Liste an (als Zeichenkette, in der die Werte aller Elemente als Zeichenketten aneinandergehängt sind). |
Meine Blöcke
| Kopfblock/Anweisung | |
|---|---|
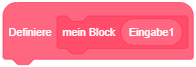 |
Beginn für das selbst definierte Skript “mein Block” des Objekts mit einem Parameter “Eingabe1” (Methodendefinition). |
 |
Führt das selbst definierte Skript “mein Block” des Objekts aus (Methodenaufruf). |
Erweiterungen
Malstift
| Anweisungen | |
|---|---|
 |
Entfernt alle bisher gezeichneten Zeichenspuren und “Abdrücke” vom Bühnenhintergrund. |
 |
Zeichnet die Grafik des Objekts an seiner aktuellen Position auf den Bühnenhintergrund. |
  |
Schaltet den Zeichenstift ein oder aus. Solange der Stift eingeschaltet ist, wird bei jeder Bewegung des Objekts eine Spur auf dem Bühnenhintergrund gezeichnet. Zum Zeichnen wird die momentan festgelegte Stiftfarbe und -breite verwendet. |
 |
Setzt die Stiftfarbe zum Zeichnen auf die angegebene Farbe. |
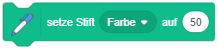 |
Setzt den Wert für den Farbton, die Sättigung, Helligkeit oder Transparenz des Zeichenstifts auf den angegebenen Wert (Auswahl des Attributs über das Symbol ▾).2 |
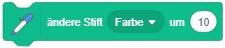 |
Addiert den angegebenen Wert zum aktuellen Wert für Farbton, Sättigung, Helligkeit oder Transparenz des Zeichenstifts.[] |
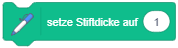 |
Setzt die Stiftbreite zum Zeichnen auf den angegebenen Wert (Pixel). |
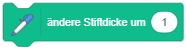 |
Addiert den angegebenen Wert zur aktuellen Stiftbreite (Pixel). |
Musik
| Anweisungen | |
|---|---|
 |
Spielt einen Ton des ausgewählten Schlaginstruments ab (Auswahl über das Symbol ▾). |
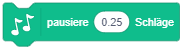 |
Wartet die angegebene Anzahl von Schlägen. |
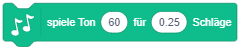 |
Spielt einen Ton mit der angegebenen Dauer ab und wartet für die entsprechende Zeitspanne.1 Dazu wird das momentan für die Musikwiederfabe festgelegte Instrument verwendet. |
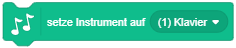 |
Legt ein Instrument für die Musikwiedergabe fest (Auswahl über das Symbol ▾). |
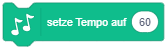 |
Legt das Tempo der Musikwiedergabe auf den angegebenen Wert fest (Schläge pro Sekunde). |
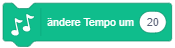 |
Addiert den angegebenen Wert zum aktuellen Tempo der Musikwiedergabe. |
| Werte | |
|---|---|
 |
Gibt als Wert das aktuelle Tempo der Musikwiedergabe an (Schläge pro Sekunde). |
Text zu Sprache
| Anweisungen | |
|---|---|
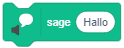 |
Spricht den angegebenen Text und pausiert das Skript, bis die Sprachausgabe abgeschlossen ist.1 |
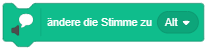 |
Legt die Stimme für die Sprachausgabe fest (Auswahl über das Symbol ▾): Alt (weiblich), Tenor (männlich), Quietschen (sehr hoch), Riese (sehr tief) oder Kätzchen (gibt jedes Wort als “Miau” aus). |
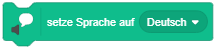 |
Legt die Wiedergabesprache fest (Auswahl über das Symbol ▾). |
Übersetzen
| Werte | |
|---|---|
 |
Gibt als Wert die Übersetzung des angegebenen Textes in die ausgewählte Zielsprache an (Auswahl über das Symbol ▾). Die Ausgangssprache wird automatisch erkannt. |
 |
Gibt als Wert die Sprache der Scratch-Oberfläche an (Auswahl über das Symbol  im Menü). im Menü). |
Videoerfassung
| Ereignisse | |
|---|---|
 |
Das angehängte Skript wird ausgeführt, wenn die im Kamerabild gemessene Bewegungsintensität im Bereich des Objekts, zu dem das Skript gehört, über den angegebenen Grenzwert steigt (0 bis 100). Gehört das Skript zur Bühne, wird die Bewegungsintensität im Bereich des Hintergrundbildes ausgewertet. |
| Anweisungen | |
|---|---|
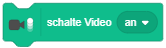 |
Schaltet die Videoerfassung an (gespiegelt oder normal) oder aus (Auswahl über das Symbol ▾). |
 |
Legt die Transparenz für das Kamerabild-Overlay auf dem Bühnenhintergrund fest (in Prozent). Bei einem Wert von 100 (vollständig transparent) wird das Kamerabild nicht angezeigt, die Videoerfassung findet aber trotzdem statt. |
| Werte | |
|---|---|
 |
Gibt als Wert die Intensität oder Richtung der im Kamerabild gemessenen Bewegung an. Dabei wird entweder die Bewegung auf dem Hintergrundbild oder auf dem Objekt gemessen (Auswahl des Ziels über die rechte Auswahlliste ▾). In der linken Auswahlliste kann zwischen Bewegungsintensität und Richtung gewählt werden. Die Bewegungsintensität wird auf einer Skala von 0 (keine Bewegung) bis 100 (sehr starke Bewegung) gemessen, die Richtung als Winkel in Grad (relativ zur momentanen Richtung des Objekts). |
-
Diese Anweisung hat eine festgelegte Dauer. Während dieser Dauer wird das Skript pausiert. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
-
Mit einem Klick auf das Symbol ▾ rechts im Block kann aus den verschiedenen Grafikeffekten ausgewählt werden. Die Wertebereiche und genauere Beschreibungen der Grafikeffekte können im Scratch-Wiki nachgelesen werden: https://de.scratch-wiki.info/wiki/Grafikeffekte ↩︎ ↩︎
-
Unsichtbare Objekte erscheinen nicht auf der Bühne und können nicht mit der Maus angeklickt werden. Außerdem können sie keine anderen Objekte berühren. Auf andere Ereignisse reagieren sie aber nach wie vor. ↩︎ ↩︎
-
Mit einem Klick auf das Symbol ▾ rechts im Block kann aus den verschiedenen Wiedergabeeffekten ausgewählt werden. Für die Stereo-Aussteuerung kann ein Wert zwischen -100 (nur links abspielen) und 100 (nur rechts abspielen) angegeben werden. ↩︎
-
Die “Stoppuhr” von Scratch misst die Sekunden, die seit dem letzten Programmstart mit
 vergangen sind (oder vor dem ersten Programmstart seit dem Starten der Scratch-Entwicklungsumgebung) bzw. seitdem die Stoppuhr zuletzt auf 0 zurückgesetzt wurde. ↩︎ ↩︎ ↩︎
vergangen sind (oder vor dem ersten Programmstart seit dem Starten der Scratch-Entwicklungsumgebung) bzw. seitdem die Stoppuhr zuletzt auf 0 zurückgesetzt wurde. ↩︎ ↩︎ ↩︎ -
Eine neue Nachricht lässt sich erstellen, indem auf das Symbol ▾ rechts im Block geklickt und “Neue Nachricht” gewählt wird. ↩︎
-
Das Skript wird hier also pausiert, bis alle Skripte, die mit einem passenden Ereignisblock “Wenn ich … empfange” beginnen, zuende ausgeführt wurden. ↩︎
-
Der Abbruch aller Skripte hat denselben Effekt wie das Beenden des Programms durch Klicken auf das Stop-Symbol
 . ↩︎
. ↩︎ -
Wenn das zu klonende Objekt ein Skript mit dem Ereignisblock “Wenn ich als Klon entstehe” besitzt, wird dieses zum Zeitpunkt des Klonens für das neu entstandene Objekt (den Klon) ausgeführt. ↩︎
-
Beim Programmende werden automatisch alle Klone von Objekten gelöscht. ↩︎
-
Mit diesem Werteblock können auch die Werte von Objektvariablen oder globalen Variablen ermittelt werden. Globale Variablen befinden sich hier in der Auswahlliste der Bühne. ↩︎
-
Wenn das Skript zu einem Objekt gehört, können hier Variablen des Objekts selbst und globale Variablen gewählt werden. Gehört das Skript zur Bühne, können nur globale Variablen gewählt werden. ↩︎
-
Wenn das Skript zu einem Objekt gehört, können hier Listen des Objekts selbst und globale Listen gewählt werden. Gehört das Skript zur Bühne, können nur globale Listen gewählt werden. ↩︎
2. Informationsdarstellung
2.1 Informationsdarstellung
Einleitung
In diesem Modul beschäftigen wir uns damit, wie Informationen auf Grundlage von Daten dargestellt werden. Dazu sollen zuerst die zentralen Begriffe erläutert werden.
Informationen und Daten sind zentrale Objekte der Informatik, wie in den Fachanforderungen zum inhaltsbezogenen Kompetenzbereich “Daten und Informationen” festgestellt wird:
Informatik ist die Wissenschaft von der systematischen Darstellung, Speicherung, Verarbeitung und Übertragung von Informationen.
Insofern sind Daten als Repräsentation von Informationen Grundlage jeglicher Informationsverarbeitung.
Obwohl die Begriffe “Daten” und “Informationen” in der Umgangssprache oft gleichbedeutend verwendet werden, muss deutlich zwischen beiden Begriffen unterschieden werden:
- Daten (Singular: “Datum”) sind einzelne “nackte” Werte oder Fakten, aus denen Information besteht, die aber nicht gleichbedeutend mit Information sind.1 Erst indem Daten strukturiert, in einen bestimmten Kontext gesetzt und interpretiert werden, entsteht aus Daten Information.
- Information besteht nach der gängigen Definition aus mindestens einem Datum oder mehreren Daten, die wohlgeformt sind und Bedeutung tragen.2
Vereinfacht ausgedrückt ist also Information = Daten + Bedeutung.
Information lässt sich durch Daten darstellen und Daten liefern Information, indem sie gedeutet werden.
Beispiel: Die Zeichenfolgen 10:30, 12:15, 15:20 sind Daten, aber noch keine Information, da ihre Bedeutung nicht bekannt ist. Es könnte sich um Uhrzeiten handeln, aber auch um Punktestände von Basketballspielen oder um Abstimmungsergebnisse. Auch wenn durch den Kontext festgelegt ist, dass es sich um Uhrzeiten handelt, beschreiben die Daten noch keine brauchbare Information – dazu benötigen wir beispielsweise noch als weiteres Vorwissen, dass sie die nächsten Abfahrtzeiten eines bestimmten Zuges angeben.
Syntax und Semantik
Die “Wohlgeformtheit” der Daten bedeutet, dass sie bezüglich bestimmter Regeln richtig repräsentiert sind, also beispielsweise nur zulässige Zeichen enthalten und eine bestimmte Struktur haben. Regeln zur Zusammensetzung von Zeichenfolgen aus einzelnen Zeichen werden als Syntax bezeichnet.3 Die Interpretation der Datenrepräsentationen, also die Zuordnung von Bedeutung zu den Zeichenfolgen, heißt Semantik.
Beispiel: Für Daten, die in Formulare eingetragen werden, wird oft eine Syntax festgelegt, die vorschreibt, wie die Daten formal anzugeben sind. Für eine Uhrzeit kann etwa vorgegeben sein, dass sie mit 2 Ziffern beginnt, danach kommt ein Doppelpunkt und anschließend weitere 2 Ziffern. Zeichenfolgen wie 1:30 oder 10 Uhr wären hier also syntaktisch nicht korrekt. Die Zeichenfolge 99:99 wäre in diesem Beispiel dagegen syntaktisch korrekt, aber semantisch nicht sinnvoll.
Einzelne Daten liefern meist nur wenig Information. Durch Datenverarbeitung lässt sich aus mehreren Daten weitere Information ableiten. Damit Information nützlich oder brauchbar ist, muss also eine Fragestellung vorliegen, zu deren Beantwortung die bedeutungstragenden, wohlgeformten Daten verwendet werden können.
Einzelne Temperaturmesswerte stellen beispielsweise Daten mit einem geringen Informationsgehalt dar, aus denen wir relevantere Information ableiten können, indem wir etwa den Mittelwert, Höchstwert oder Verlauf für einen bestimmten Zeitraum auswerten und ggf. in Bezug zu anderen Messdaten oder Ereignissen setzen. Dabei muss natürlich berücksichtigt werden, dass durch statistische Auswertungen auch falsche Schlüsse gezogen werden können.
Ein wichtiger Anwendungsbereich der Informatik – das Data Mining – beschäftigt sich genau damit, Informationen aus Messdaten zu gewinnen, indem computergestützt nach Mustern, Trends oder Zusammenhängen in meist sehr großen Datenbeständen (“Big Data”) gesucht wird, die bisher unbekannt und nützlich sind. Dazu werden auch in zunehmendem Maße Verfahren der Künstlichen Intelligenz verwendet.
Codierung
Zur Repräsentation von Information bzw. der zugrundeliegenden Daten werden bestimmte Zeichen und syntaktische Regeln verwendet. Dabei kann dieselbe Art von Daten auch durch verschiedene Repräsentationen dargestellt werden: Ein Name lässt sich beispielsweise sowohl durch Buchstaben, im Morse-Code oder mit Hilfe des Fingeralphabets darstellen; ein Kalenderdatum kann im Format 12. August 2021, 12.08.2021, 2021-08-12 oder einfach als 18851 (= Tage seit dem 1.1.1970) darstellt werden.

Codierung bezeichnet die Repräsentation abstrakter Information in einem konkreten Zeichensystem gemäß vereinbarter syntaktischer und semantischer Regeln, und wird darüber hinaus auch als Begriff für die Umwandlung einer Datenrepräsentation in eine andere verwendet.
Im Alltag sind wir umgeben von codierter Information: Beim Einkaufen finden sich Strichcodes zur Kennzeichnung auf Lebensmitteln, Büchern und anderen Artikeln, auf Eiern gibt ein Erzeugercode deren Herkunft an, Kfz-Kennzeichen codieren Information über die Zulassung von Fahrzeugen. Der QR-Code als zweidimensionales Pendant zum Strichcode ist allgegenwärtig, um schnell Informationen durch ein Kamerabild mit dem Handy abzufragen. In Chatnachrichten codieren wir Informationen piktografisch durch Emojis oder durch Abkürzungen, deren Bedeutungen bekannt sind.
Solche Beispiele eignen sich gut als Einstiegspunkt für das Thema “Codierung” im Schulunterricht.
Beispiel: Kfz-Kennzeichen
Ein Kfz-Kennzeichen (siehe Wikipedia) beginnt mit einem Unterscheidungszeichen (1–3 Buchstaben) für den Standort des Fahrzeugs, gefolgt von der Erkennungsnummer (in der Regel 1–2 Buchstaben, gefolgt von 1–4 Ziffern ohne führende Nullen, zusammen mit dem Unterscheidungszeichen aber nicht mehr als 8 Zeichen). Die Buchstaben- und Zifferngruppen werden üblicherweise durch Leerzeichen, seltener durch Bindestriche getrennt dargestellt. Diese Beschreibung legt sowohl den Aufbau (Syntax) als auch die Interpretation (Semantik) der Kennzeichen fest.

Beispiel: Das Kfz-Kennzeichen ECK IG 987 gibt an, dass der reguläre Standort des Fahrzeugs im Kreis Rendsburg-Eckernförde (ECK) liegt, seine Erkennungsnummer ist IG 987.
Beispiel: Eierkennzeichnung
Der Erzeugercode (siehe Wikipedia), der auf Hühnereiern im Handel in der EU zu finden ist, codiert Informationen über die Herkunft des Eis und die Haltungsform der Hennen. Der Code besteht aus Ziffern und Buchstaben und hat in Deutschland die Form (Syntax): eine Ziffer zwischen 0 und 3, zwei Buchstaben, sieben Ziffern, wobei die Ziffern- und Buchstabengruppen durch Bindestriche getrennt werden.4
Die Bedeutung (Semantik) des Codes ist folgendermaßen:
- Die erste Ziffer gibt die Haltungsform an (0 für Ökologische Erzeugung, 1 für Freilandhaltung, 2 für Bodenhaltung, 3 für Käfighaltung).
- Die beiden Buchstaben geben das Herkunftsland an (DE für Deutschland).
- Der letzte Teil gibt die Betriebsnummer an, wobei in Deutschland die ersten beiden Stellen das Bundesland (01 für Schleswig-Holstein), Stellen 3–6 den Betrieb und Stelle 7 den Stall identifizieren.
Beispiel: Der Erzeugercode 1-DE-0123456 gibt an, dass das Ei aus Freilandhaltung (1) in Schleswig-Holstein (DE-01) vom Betrieb mit der Kennnummer 2345 aus Stall 6 stammt.
In beiden Beispielen (Kfz-Kennzeichen und Erzeugercode) hat der Code eine bestimmte Struktur und besteht aus einer begrenzten Menge von Zeichen, wobei bestimmte Zeichen nur an bestimmten Positionen im Code erlaubt sind. Dabei werden Teilinformationen durch bestimmte Teile des Codes repräsentiert, beispielsweise ein Land (Herkunftsland des Eis) durch zwei Buchstaben an Position 2 und 3 im Erzeugercode oder ein Land-/Stadtkreis (Standort des Kfz) durch 2–3 Buchstaben zu Beginn des Kfz-Kennzeichens.
Digitale Codierung
Bei der rechnergestützten Informationsverarbeitung werden Informationen durch digitale Codes dargestellt, das bedeutet, dass sie in Form von endlich vielen diskreten Werten – also Werten aus einem abzählbaren und ebenfalls endlichen Wertebereich – dargestellt werden. Digitale Daten lassen sich also unter anderem durch endliche Folgen von Ganzzahlen beschreiben. Das Gegenstück sind analoge Daten, die aus stufenlos darstellbaren Werten bestehen.
Beispiel: Eine Digitaluhr (ohne Sekundenanzeige) repräsentiert die kontinuierliche (analoge) Tageszeit durch zwei diskrete Werte: eine von 24 Stunden und eine von 60 Minuten, es werden also nur 24⋅60 = 1440 verschiedene Zustände der Zeit unterschieden.
Der Prozess, analoge Daten in digitale Daten umzuwandeln, wird als Digitalisierung bezeichnet. Typische Beispiele sind die Digitalisierung von Schalldruckmessungen bei Tonaufnahmen mit einem Mikrofon oder die Digitalisierung von Helligkeitswerten beim Scannen von analogen Dokumenten. Inzwischen liefern die meisten Aufnahmegeräte und Sensoren, denen wir im Alltag begegnen, von vornherein digitale Daten, siehe beispielsweise die Bild- und Sprachaufnahme mit dem Handy oder die Messergebnisse eines Digitalthermometers.
Für IT-Systeme wie Rechner oder Netzwerkgeräte ist insbesondere die Darstellung durch binäre Codes relevant, also durch endliche Folgen der Werte 0 und 1, da Daten bei solchen Systemen aus technischen Gründen auf diese Werte intern (im Speicher, bei der Datenübertragung) repräsentiert werden.
Ziel dieses Moduls ist es, einen Überblick über verschiedene Methoden zu bekommen, wie Informationen digital repräsentiert werden können und konkrete Anwendungsbeispiele untersuchen: unter anderem Dateiformate für Texte und Bilder und die Darstellung von Informationen im Internet in Form von HTML-Dokumenten.
In den ersten Lektionen werden wir uns systematisch mit der digitalen bzw. speziell der binären Codierung verschiedener Arten von Daten beschäftigen – konkret von Zahlen und Textzeichen (vgl. Fachanforderungen D10/11) sowie Bildern (vgl. Fa. D24/25) – und anschließend Verfahren zur grafischen Codierung digitaler Daten (u. a. in Form von Barcodes) und zur Datenkompression untersuchen (vgl. Fa. D12/13).
-
Laut Duden sind Daten ganz allgemein durch Beobachtungen, Messungen u. a. gewonnene (Zahlen-)Werte und darauf beruhende Angaben, siehe https://www.duden.de/rechtschreibung/Daten (Stand August 2021) ↩︎
-
siehe z. B. Luciano Floridi: Information: A Very Short Introduction, Oxford University Press, 2010 ↩︎
-
Der Begriff “Zeichen” muss hier in einem sehr allgemeinen Sinne verstanden werden, so lassen sich natürlich auch Zusammensetzungsregeln – also eine Syntax – für grafische oder akustische Daten festlegen. ↩︎
-
In anderen Ländern kann die letzte Zeichengruppe (die Betriebsnummer) auch Buchstaben enthalten und länger oder kürzer sein. ↩︎
2.2 Codierung digitaler Daten
Zuerst werden wir uns mit der digitalen Darstellung von Zahlenwerten als elementaren Daten in verschiedenen Zahlensystemen beschäftigen, insbesondere im Binärsystem.
Als Aufgabe zum Einstieg vorweg: Der Bahnhof St. Gallen in der Schweiz besitzt seit 2018 eine Uhr der besonderen Art. Finden Sie heraus, wie spät es auf diesem Bild gerade ist? Als Tipp: Die obere Zeile stellt die Stunden dar, die mittlere die Minuten und die untere die Sekunden.

Bits und Bytes
Die einfachste Form der digitalen Darstellung ist die Binärdarstellung, in der nur zwei verschiedene Werte verwendet werden, die üblicherweise als 0 und 1 dargestellt werden. Diese kleinste digitale Informationseinheit wird als Bit bezeichnet. Binärdaten werden durch Bitfolgen, also Folgen von Nullen und Einsen dargestellt.
Digitale Daten lassen sich dabei immer auch durch Binärdaten repräsentieren, indem jedem der abzählbar vielen Werte eine eindeutige Bitfolge zugewiesen wird.
Beispiel: Die Minuten einer digitalen Uhrzeit können 60 verschiedene Werte annehmen. Jeder Minutenwert lässt sich binär mit 6 Bit beschreiben, da eine Bitfolge der Länge 6 insgesamt 26 = 64 verschiedene Zustände einnehmen kann.
Die Binärdarstellung ist besonders relevant, da Rechner Daten intern als Bitfolgen speichern und verarbeiten. Üblicherweise verarbeiten Rechner Bits aber nicht einzeln, sondern in 8-Bit-Blöcken. Ein solcher 8-Bit-Block wird als Byte bezeichnet und kann entsprechend 28 = 256 viele Zustände einnehmen, die sich als Ganzzahlen von 0 bis 255 interpretieren lassen.
Die Binärdarstellung von Zahlen ist in vielen Anwendungsfällen hilfreich, beispielsweise um Daten im Speicher zu interpretieren, die Funktionsweise eines Rechners auf Hardwareebene zu verstehen, die Kommunikation zwischen Rechnern in Netzwerken oder die Adressierung von Rechnern in hierarchischen Rechnernetzen nachzuvollziehen.
Binärzahlen
Wenn wir binäre Daten untersuchen, macht es Sinn, die einzelnen Werte nicht im Dezimalsystem, sondern als Binärzahl darzustellen, also im Dualsystem (“Zweiersystem”), dem Stellenwertsystem zur Basis 2. Im Dualsystem werden Zahlen nur mit den beiden Ziffern 0 und 1 dargestellt. Die Stellenwerte sind durch die Potenzen der Basis 2 festgelegt, also (von rechts nach links) 20 = 1, 21 = 2, 22 = 4, … – analog zu den Stellenwerten im Dezimalsystem: 100 = 1, 101 = 10, 102 = 100, …
Die folgende Tabelle stellt die Zweierpotenzen bis 216 dar, um einen Eindruck von den Größenordnungen zu bekommen:
| Exponent n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Zweiterpotenz 2n | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16 384 | 32 768 | 65 536 |
Um eine Binärzahl in eine Dezimalzahl umzuwandeln, werden die Ziffern mit den entsprechenden Stellenwerten (= Zweierpotenzen) multipliert und summiert (oder einfacher: Es werden diejenigen Zweierpotenzen summiert, an deren Stellen die Ziffer 1 steht).
Tool: In dieser interaktiven Anzeige können Sie die Binärdarstellung von Ganzzahlen selbst untersuchen. Klicken Sie auf die oberen Binärziffern, um ihre Werte zu ändern.
In der Binärdarstellung entspricht jede Ziffer einem Datenbit. Ein Byte ist also durch eine Binärzahl mit 8 Stellen repräsentiert (ggf. mit führenden Nullen).
Beispiel: Die Binärzahl 00101010 entspricht der Dezimalzahl 25 + 23 + 21 = 32 + 8 + 2 = 42.
Um eine Dezimalzahl ins Binärsystem umzuwandeln, wird die Zahl wiederholt mit Rest durch die Basis 2 geteilt, bis der Quotient 0 ergibt. Die Werte der Teilungsreste ergeben dann von oben nach unten gelesen die Ziffern der Binärdarstellung von rechts nach links gelesen.
Beispiel: Hier wird die Zahl 71 ins Binärsystem umgewandelt:
- 71 / 2 = 35 Rest 1
- 35 / 2 = 17 Rest 1
- 17 / 2 = 8 Rest 1
- 8 / 2 = 4 Rest 0
- 4 / 2 = 2 Rest 0
- 2 / 2 = 1 Rest 0
- 1 / 2 = 0 Rest 1
Die Binärdarstellung mit 8 Stellen lautet hier also 01000111.
Hexadezimalzahlen
Da Byte-Folgen in der Binärdarstellung schnell sehr lang und unübersichtlich werden, wird zur Darstellung von Bytes statt des Binärsystems oft auch das Hexadezimalsystem verwendet, in dem Zahlen in einem Stellenwertsystem zur Basis 16 dargestellt werden. Neben den Zeichen 0 bis 9 werden hier die Buchstaben A bis F für die sechs zusätzlichen Ziffern verwendet (A entspricht dabei der Dezimalzahl 10 und F der Dezimalzahl 15).
| Dezimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Hexadezimal | 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
Tool: In dieser interaktiven Anzeige können Sie die Hexadezimaldarstellung von Ganzzahlen selbst untersuchen. Klicken Sie auf die oberen Hexadezimalziffern, um ihre Werte zu ändern.
Beispiel:
Die Hexadezimalzahl CAFE entspricht der Dezimalzahl 12·163 + 10·162 + 15·16 + 14·1 = 51966.
Um eine Dezimalzahl ins Hexadezimalsystem umzuwandeln, wird die Zahl wiederholt mit Rest durch 16 geteilt.
Beispiel:
Für die Dezimalzahl 172 gilt: 172 / 16 = 10 Rest 12, also lautet ihre Hexadezimaldarstellung AC.
Ein Byte entspricht im Hexadezimalsystem jeweils einer Hexidezimalzahl mit zwei Ziffern (ggf. mit einer führenden Null).
Die Umrechnung zwischen Binär- und Hexadezimalsystem lässt sich sehr einfach lösen, indem je 4 Binärziffern zusammengefasst und durch die entsprechende Hexadezimalziffer ersetzt werden:
| Binär | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| Hexadezimal | 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Binär | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| Hexadezimal | 8 |
9 |
A |
B |
C |
D |
E |
F |
Konvertierung
Tool: Mit diesem Formular können Sie die Repräsentation von Ganzzahlen zwischen dem Dezimalsystem, Hexadezimalsystem und Binärsystem umrechnen.
Größeneinheiten
Um größere Datenmengen von Bits und Bytes zu beschreiben, werden meistens die bekannten Dezimalpräfixe für Maßeinheiten (auch SI-Präfixe genannt) verwendet, mit denen 1000er-Potenzen von Bytes zu je einer Maßeinheit zusammengefasst werden:
| Symbol | Name | Wert | Beispiele für die Größenordnung |
|---|---|---|---|
| B | Byte | 1 B = 8 bit | Zeichen in einer Textdatei |
| kB | Kilobyte | 1 kB = 1000 B = 103 B | Normseite (max. 1.800 Zeichen) |
| MB | Megabyte | 1 MB = 1000 kB = 106 B | Bild- und Audiodateien, Videoclips |
| GB | Gigabyte | 1 GB = 1000 MB = 109 B | Bild-/Audiosammlungen, unkomprimierte Videos |
| TB | Terabyte | 1 TB = 1000 GB = 1012 B | Eine oder mehrere Festplatten |
Daneben werden auch Binärpräfixe (auch IEC-Präfixe genannt) verwendet, die Vielfache bestimmter Zweierpotenzen bezeichnen (hier: Potenzen von 1024), da binäre Datenmengen aus technischen Gründen oft in diesen Größenordnungen auftreten. Grund dafür ist, dass die SI-Präfixe früher je nach Kontext mal als Dezimalpräfixe und mal als Binärpräfixe verwendet wurden, z. B. konnte mit “1 Kilobyte” entweder 1000 Byte oder 1024 Byte gemeint sein. Um hier Klarheit zu schaffen, wurden Ende der 90er Jahre von der IEC (International Electrotechnical Commission) eigene Präfixe für Zweierpotenzen eingeführt:1
| Symbol | Name | Wert |
|---|---|---|
| KiB | “Kibibyte” | 1 KiB = 1024 B = 210 B |
| MiB | “Mebibyte” | 1 MiB = 1024 KiB = 220 B |
| GiB | “Gibibyte” | 1 GiB = 1024 MiB = 230 B |
| TiB | “Tebibyte” | 1 TiB = 1024 GiB = 240 B |
Codierung von Zahlen
Ganzzahlen ohne Vorzeichen
Natürliche Zahlen (also vorzeichenlose Ganzzahlen) werden in Rechnern als Bitfolgen codiert, wobei sich die Werte der einzelnen Bits aus der Binärdarstellung der Zahl ergeben.
Formel: Für die Bitfolge b1 b2 … bN-1 bN der Länge N ist die entsprechende Dezimalzahl d also durch die folgende Formel gegeben: $$d = b_1 \cdot 2^{N-1} + b_2 \cdot 2^{N-2} + … + b_{N-1} \cdot 2 + b_N$$
Dabei wird üblicherweise eine feste Länge für die Bitfolgen verwendet – es wird also festgelegt, also wie vielen Bits eine Zahl besteht. In der Praxis werden meistens 1, 2, 4 oder 8 Byte verwendet. Der Umfang des darstellbaren Zahlenbereichs ist durch die Anzahl an Bits, die zur Darstellung einer Zahl verwendet werden, eingeschränkt.
Die folgende Tabelle zeigt einen Ausschnitt aus dem Coderaum der 8-Bit-Ganzzahlen:
| Binär | 00000000 | 00000001 | … | 00101010 | … | 01111111 | 10000000 | 10000001 | … | 10101010 | … | 11111111 |
| Dezimal | 0 | 1 | … | 42 | … | 127 | 128 | 129 | … | 170 | … | 255 |
Wird 1 Byte (= 8 Bit) pro Zahl verwendet, lassen sich damit 28 verschiedene Werte darstellen, also alle natürlichen Zahlen von 0 bis einschließlich 28-1 = 255. Allgemein wäre für N Byte (= 8N Bit) die größte darstellbare natürliche Zahl 28N-1.
| Bits (Bytes) pro Zahl | Darstellbarer Zahlenbereich | |
|---|---|---|
| 8 Bit (1 Byte) | 0, …, 28-1 = 255 | |
| 16 Bit (2 Byte) | 0, …, 216-1 = 65 535 | |
| 32 Bit (4 Byte) | 0, …, 232-1 = 4 294 967 295 (ca. 4,3 Milliarden) | |
| 64 Bit (8 Byte) | 0, …, 264-1 = 18 446 744 073 709 551 615 (ca. 18,4 Trillionen) |
Ganzzahlen mit Vorzeichen
Damit sich auch negative Ganzzahlen (bzw. allgemeiner vorzeichenbehaftete Ganzzahlen) darstellen lassen, gibt es verschiedene Möglichkeiten. Die einfachste Variante besteht darin, dass das erste Bit der Bitfolge als Vorzeichenbit verwendet wird (0 für positives Vorzeichen, 1 für negatives Vorzeichen). Die Darstellung der Zahl -42 als 8-Bit-Zahl mit Vorzeichenbit lautet so beispielsweise: 10101010
Da hier 7 Bit für den Betrag ohne Vorzeichen übrigbleiben, wäre der darstellbare Zahlenbereich -127 bis 127. Bei 16 Bit lassen sich die Zahlen -32 767 bis 32 767 darstellen (es gilt: 215-1 = 32 767).
Die folgende Tabelle zeigt einen Ausschnitt aus dem Coderaum der 8-Bit-Ganzzahlen in der Darstellung mit Vorzeichenbit:
| Binär | 00000000 | 00000001 | … | 00101010 | … | 01111111 | 10000000 | 10000001 | … | 10101010 | … | 11111111 |
| Dezimal | 0 | 1 | … | 42 | … | 127 | -0 | -1 | … | -42 | … | -127 |
Diese Darstellung hat allerdings zwei Nachteile: Zum einen ist die Darstellung der Null uneindeutig, da auch sie zwei Repräsentationen besitzt (mit Vorzeichenbit 0 oder 1, also quasi “+0” und “-0”).
Zum anderen muss beim Addieren von Ganzzahlen in dieser Darstellung unterschieden werden, ob Summanden negativ sind und in diesem Fall ein anderer Algorithmus verwendet werden. Dieses Problem entsteht dadurch, dass die negativen Zahlen im Coderaum “falschherum” angeordnet sind (von der größten zur kleinsten).
Beispiel: Werden die 8-Bit-Repräsentationen der Zahlen -42 und 1 ohne Rücksicht auf das Vorzeichenbit summiert, ist das Ergebnis 10101011, was der Zahl -43 entspricht, nicht der erwarteten Zahl -41.
Daher verwenden Rechner in der Regel ein anderes Format zur Binärcodierung von negativen Ganzzahlen, die sogenannte Zweierkomplementdarstellung: Die erste Hälfte der N-Bit-Binärcodes stellt die nicht-negativen Ganzzahlen von 0 bis 2N-1-1 dar, danach folgen die negativen Zahlen von 2N-1 bis -1.
Auf diese Weise wird das doppelte Vorkommen der Null verhindert, die Null wird nun nur noch durch eine Folge aus 0-Bits repräsentiert (hier: 00000000). Außerdem liefert die binäre Addition von Ganzzahlen hier unabhängig von den Vorzeichen der Summanden das richtige Ergebnis, da die negativen Zahlen im Coderaum “richtigherum” angeordnet sind (also in aufsteigender Reihenfolge).
Die folgende Tabelle zeigt einen Ausschnitt aus dem Coderaum der 8-Bit-Ganzzahlen mit Vorzeichen in der Zweierkomplementdarstellung:
| Binär | 00000000 | 00000001 | … | 00101010 | … | 01111111 | 10000000 | 10000001 | … | 11010110 | … | 11111111 |
| Dezimal | 0 | 1 | … | 42 | … | 127 | -128 | -127 | … | -42 | … | -1 |
Auch bei der Zweierkomplementdarstellung übernimmt das erste Bit die Rolle eines Vorzeichenbits – sein Wert bestimmt, ob eine Bitfolge eine negative oder nicht-negative Zahl darstellt. Bei 8 Bit werden also durch die Bitfolgen 00000000 bis 01111111 alle nicht-negativen Zahlen dargestellt (0 bis 27-1 = 127) und durch 10000000 bis 11111111 alle negativen Zahlen (-27 = -128 bis -1).
Um das Vorzeichen einer Zahl zu ändern, kann ein sehr einfacher Algorithmus verwendet werden: Es werden alle Bits der Binärdarstellung der Zahl “gekippt” (invertiert) und zum Ergebnis 1 hinzuaddiert. Diese Operation wird als Zweierkomplement bezeichnet (daher der Name dieser Darstellung).
Beispiel: Es soll die Zweierkomplementdarstellung der Zahl -42 mit 8 Bit berechnet werden:
00101010← Binärdarstellung von 42 mit 8 Bit11010101← Invertieren aller Bits11010110← Hinzuaddieren von 1
Tool: In dieser interaktiven Anzeige können Sie die Zweierkomplementdarstellung selbst untersuchen. Klicken Sie auf die oberen Binärziffern, um ihre Werte zu ändern.
In der Zweierkomplementdarstellung mit N Bit können vorzeichenbehaftete Ganzzahlen aus dem Bereich -2ᴺ⁻¹ bis 2ᴺ⁻¹-1 repräsentiert werden. Das erste (linke) Bit gibt das Vorzeichen an.
Ist das Vorzeichenbit 0, entspricht die Repräsentation der vorzeichenlosen Ganzzahl. Anderenfalls stellt die Bitfolge diejenige negative Ganzzahl dar, die man erhält, wenn von der entsprechenden vorzeichenlosen Ganzzahl der Wert 2ᴺ abgezogen wird. Die Darstellung im Zweierkomplement kann also auch ganz einfach interpretiert werden, indem die höchste (linke) Stelle der Binärzahl, die 2ᴺ⁻¹ entspricht, negativ in die Summe eingeht.
Formel: Für die Bitfolge b1 b2 … bN-1 bN der Länge N ist die entsprechende Dezimalzahl d also durch die folgende Formel gegeben: $$d = -b_1 \cdot 2^{N-1} + b_2 \cdot 2^{N-2} + … + b_{N-1} \cdot 2 + b_N$$
Rationale Zahlen
Um rationale Zahlen oder “Kommazahlen” binär darzustellen, gibt es ebenfalls mehrere Möglichkeiten. Sehr einfach zu interpretieren ist die Darstellung als Festkommazahl. Hier wird festgelegt, dass eine bestimmte Anzahl von Bits zur Darstellung der Nachkommastellen verwendet wird. Bei einer Repräsentation mit 8 Bit kann beispielsweise vereinbart werden, dass die ersten 5 Bit die Stellen vor dem Komma darstellen und die letzten 3 Bit für die Nachkommastellen stehen. Die Stellen entsprechen dann von links nach rechts den Zweierpotenzen 24, …, 20, 2-1, 2-2 und 2-3. Zur Erinnerung: 2-n ist gleich 1 / 2n.
Beispiel: Die Binärdarstellung von 10.75 als Festkommazahl mit 8 Bit, davon 3 Nachkommastellenbits, lautet: 01010110. Die linken 5 Stellen codieren die Ganzzahl 10, die rechten 3 Stellen den Nachkommaanteil 1·2-1 + 1·2-2 + 0·2-3 = 0.5 + 0.25 = 0.75.
Tool: In dieser interaktiven Anzeige können Sie die Binärdarstellung von Festkommazahlen selbst untersuchen. Klicken Sie auf die oberen Binärziffern, um ihre Werte zu ändern, und verwenden Sie die unteren Schaltflächen, um die Anzahl der Nachkommastellenbits zu ändern.
Eine Festkommazahl mit N Bit, von denen M Nachkommastellenbits sind, lässt sich als Bruch Z / 2ᴹ mit ganzzahligem Zähler Z schreiben. Ihre Binärdarstellung ist dann identisch mit der Binärdarstellung der Ganzzahl Z mit N Bit.
Die Binärdarstellung von 10.75 als 8-Bit-Festkommazahl mit 3 Nachkommastellenbits ist also identisch mit der 8-Bit-Binärdarstellung der Ganzzahl 86, da 10.75 = 86 / 2³.
Formel: Für die Bitfolge b1 b2 … bN-1 bN der Länge N mit M Nachkommstellenbits ist die entsprechende Dezimalzahl d also durch die folgende Formel gegeben: $$d = \left( b_1 \cdot 2^{N-1} + b_2 \cdot 2^{N-2} + … + b_{N-1} \cdot 2 + b_N \right) /\ 2^M$$
Rationale Zahlen mit Vorzeichen lassen sich auf dieselbe Weise repräsentieren wie Ganzzahlen mit Vorzeichen, also üblicherweise in der Zweierkomplementdarstellung.
Beispiel: Die Zweierkomplementdarstellung von -10.75 als 8-Bit-Festkommazahl mit 3 Nachkommastellenbits lautet:
01010110← Binärdarstellung von 10.7510101001← Invertieren aller Bits10101010← Hinzuaddieren von 1
Vertiefung: Byte-Reihenfolge
In Binärdateien wird die Reihenfolge der Bytes, durch die eine Ganzzahl repräsentiert wird, aus technischen Gründen manchmal umgedreht. Die 16-Bit-Darstellung der Zahl 260 lautet dann 00000100 00000001, und nicht 00000001 00000100, wie eigentlich erwartet.
Dieses Format heißt Little Endian (“kleinendiges” Format), da das Byte, dass die kleinsten Stellen enthält, vorne (links) steht. Die übliche Reihenfolge, die der Darstellung als Binärzahl entspricht, heißt entsprechend Big Endian (“großendiges” Format). Wir gehen hier in den Übungsaufgaben der Einfachheit davon aus, dass Big Endian-Codierung verwendet wird.
Übungsaufgaben
Aufgabe 1: DNS-Sequenzen
Die genetische Information von Lebewesen – das Genom – ist im Zellkern in der Desoxyribonukleinsäure (DNS) gespeichert, konkret wird sie durch die Abfolge der Nukleinbasen in den DNS-Strängen bestimmt. Dabei kommen nur vier Nukleinbasen vor (Adenin, Cytosin, Guanin und Thymin), womit sich die in der DNS gespeicherte Information durch eine Sequenz von vier Zeichen (in der Regel die Buchstaben A, C, G und T) darstellen lässt.
In dieser Aufgabe sollen die Binärdarstellung der genetischen Information und die entstehenden Datenmengen untersucht werden.
- Wie viele Bit werden benötigt, um ein Zeichen der Basensequenz zu codieren?
- Wie würde der Binärcode für die Basensequenz CGACAT in der von Ihnen gewählten Codierung lauten?
- Wie lang kann eine Basensequenz sein, die sich mit 1 MB codieren lässt?
- Die Basensequenz der DNS von Kugelfischen (Takifugu rubripes) hat eine Gesamtlänge von 365 Millionen Zeichen. Wie groß ist die Datenmenge, die zur Speicherung dieser Sequenz benötigt wird? Geben Sie den Wert in einer geeigneten Größeneinheit an.
- Bei menschlicher DNS umfasst das Genom etwa 3.1 Milliarden Basen. Zum Speichern der Daten können Sie einen USB-Stick mit 750 MB, 1 GB, 2 GB, 4 GB oder 8 GB Speicherkapazität verwenden. Welcher USB-Stick reicht hier aus?
Angenommen, in einer Binärdatei sollen mehrere unterschiedliche lange Basensequenzen gespeichert werden. Dazu wird neben A, C, G und T ein zusätzliches Trennzeichen verwendet, um kennzuzeichnen, wo eine Sequenz endet und die nächste beginnt.
- Wie viele Bit wären nun zur Codierung jedes Zeichens in der Datei nötig?
- Wie groß wäre nun eine Datei, die nur die Basensequenz von Takifugu rubripes enthält?
- Fällt Ihnen eine andere ggf. bessere Möglichkeit ein, wie sich mehrere unterschiedlich lange Sequenzen in einer Datei speichern lassen?
Aufgabe 2: Binärdatei interpretieren
In einer Binärdatei sind Informationen über die Bevölkerungsentwicklung von Kiel gespeichert. Der Dateiinhalt hat dabei das folgende Format:
- Die Datei enthält nacheinander mehrere Datensätze, die jeweils 6 Byte umfassen.
- Jeder Datensatz besteht aus den folgenden drei Daten (jeweils 2 Byte):
- die Jahreszahl als vorzeichenlose Ganzzahl
- die Bevölkerungsdifferenz zum Vorjahr als Ganzzahl mit Vorzeichen in Zweierkomplementdarstellung
- der Prozentsatz der Bevölkerungsanzahl im Vergleich zum Vorjahr als Festkommazahl mit 6 Nachkommastellenbits
Ihre Aufgabe besteht darin, den Inhalt der Binärdatei Kiel_Daten.bin zu decodieren ( Download):
00000111 11000111 00000110 00000100 00011001 00101000
00000111 11001000 00001000 00101100 00011001 00111000
00000111 11001001 11111110 11110100 00011000 11111001
Tragen Sie die in der Datei codierten Daten in die folgende Tabelle ein (als Hilfestellung ist der erste Datensatz bereits decodiert):
| Jahr | Differenz | Prozentsatz | Datensatz in der Datei (6 Byte) |
|---|---|---|---|
| 1991 | 1540 | 100.625 | 00000111 11000111 00000110 00000100 00011001 00101000 |
| ? | ? | ? | 00000111 11001000 00001000 00101100 00011001 00111000 |
| ? | ? | ? | 00000111 11001001 11111110 11110100 00011000 11111001 |
Verwenden Sie einen Binär-/Hexadezimaleditor, um die Datei zu untersuchen, z. B. den Online Editor HexEd.it.
Achten Sie darauf, den Editor so einzustellen, dass er das Format Big Endian verwendet, um Ganzzahlen zu interpretieren (z. B. in HexEd.it im linken Menü den unteren Bereich “Daten-Inspektor (Big-Endian)” durch Anklicken des Symbols + aufklappen).
-
Es wird von vielen Standardisierungsorganisationen ausdrücklich empfohlen, die SI-Präfixe ausschließlich für Zehnerpotenzen und die IEC-Präfixe für Zweierpotenzen zu verwenden. Die Akzeptanz und Verbreitung der IEC-Präfixe ist im IT-Bereich bis heute zwar eher gering, nimmt aber zu (Stand 2021). ↩︎
2.2.1 Codierung von Textdaten
Nachdem Sie die Binärdarstellung von Ganzzahlen kennengelernt haben: Wie würden Sie einen Namen binär codieren? Überlegen Sie dazu: Wie viele Bits werden pro Zeichen benötigt, um die dafür mindestens benötigten Zeichen zu codieren? Wie könnte der Name “BEA BUX” in dieser Codierung aussehen?
Sollen neben Groß- auch Kleinbuchstaben a–z dargestellt werden können, wird ein zusätzliches Bit benötigt, da sich der Zeichenumfang verdoppelt. Mit Ziffern, Satz- und Sonderzeichen wie Währungssymbolen, diakritischen Zeichen (z. B. Umlauten) und anderen Buchstaben des lateinischen Schriftsystems kommen schnell mehrere 100 Zeichen zusammen, für die unterschiedliche Codes benötigt werden. Für eine universelle Zeichencodierung, die auch umfangreichere Symbol- und Schriftsysteme wie das Chinesische oder Japanische umfasst, müssen dagegen mehrere 10 000 bis 100 000 Zeichen codierbar sein. Damit diese Daten eindeutig interpretierbar sind, muss in einem Standard festgelegt werden, durch welche Zahl welches Zeichen repräsentiert wird und wie diese Zahlenwerte binär codiert werden.
In dieser Lektion werden wir uns systematisch mit der Codierung von Textzeichen beschäftigen und die verbreiteten Standards zur Zeichencodierung (z. B. für Textdateien) untersuchen.
Zeichencodierung
Ein Zeichensatz (engl. character set oder kurz charset) beschreibt die Menge der zur Verfügung stehenden Zeichen, die dargestellt werden können, und legt für jedes Zeichen einen Zahlenwert fest. Die darstellbaren Zeichen werden also durchnummeriert. Der feste Zahlenwert eines Zeichens in einem Zeichensatz wird als Codepoint bezeichnet. Codepoints werden in der Regel hexadezimal, aber auch dezimal dargestellt.
Eine Zeichencodierung legt dagegen für jeden Codepoint bestimmte Byte-Werte fest, durch die das Zeichen binär codiert wird. Die früheren Zeichensätze wie ASCII oder ANSI (siehe unten) umfassten nicht mehr als 256 Zeichen, so dass der Unterschied zwischen Codepoint und Zeichencodierung keine Rolle spielte: Hier wurde ein Zeichen einfach durch die Binärdarstellung seines Codepoints codiert. Bei aktuellen Zeichensätzen wie Unicode, die mehrere 100 000 Zeichen umfassen, sind Codepoint und Codierung nicht unbedingt identisch, aber dazu später mehr.
Wie beginnen zunächst mit den einfachen Zeichencodierungen, in denen jedes Zeichen durch 1 Byte codiert wird.
ASCII
Der Standard ASCII (kurz für American Standard Code for Information Interchange) wurde ursprünglich bereits 1963 entwickelt. Er definiert eine 7-Bit-Zeichencodierung, die als Grundlage der meisten heute gebräuchlichen Zeichencodierungen dient. Der ASCII-Zeichensatz umfasst 27 = 128 Zeichen, die als Byte mit führendem 0-Bit dargestellt werden. Dabei stellen nur die Zeichen 32 bis 126 (hexadezimal 20 bis 7E) druckbare Symbole dar.
Die folgende Tabelle zeigt alle Zeichen und ihre Hexadezimal-Codes im ASCII-Zeichensatz (spezielle, meist nicht druckbare Zeichen sind kursiv dargestellt):
| Code (hex.) | …0 | …1 | …2 | …3 | …4 | …5 | …6 | …7 | …8 | …9 | …A | …B | …C | …D | …E | …F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0… | NUL | SOH | STX | ETX | EOT | ENQ | ACK | BEL | BS | HT | LF | VT | FF | CR | SO | SI |
| 1… | DLE | DC1 | DC2 | DC3 | DC4 | NAK | SYN | ETB | CAN | EM | SUB | ESC | FS | GS | RS | US |
| 2… | SP | ! | " | # | $ | % | & | ' | ( | ) | * | + | , | - | . | / |
| 3… | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | : | ; | < | = | > | ? |
| 4… | @ | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| 5… | P | Q | R | S | T | U | V | W | X | Y | Z | [ | \ | ] | ^ | _ |
| 6… | ` | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| 7… | p | q | r | s | t | u | v | w | x | y | z | { | | | } | ~ | DEL |
Das Zeichen SP mit dem Hexadezimal-Code 20 (dezimal 32) stellt dabei das Leerzeichen (engl. space) dar.
Beispiel:
Die Zeichenfolge “Hallo, Kiel!” wird im ASCII-Zeichencode durch die Bytefolge 48 61 6C 6C 6F 2C 20 4B 69 65 6C 21 (hexadezimal) repräsentiert.
| Zeichen | H | a | l | l | o | , | K | i | e | l | ! | |
| Code (hex.) | 48 |
61 |
6C |
6C |
6F |
2C |
20 |
4B |
69 |
65 |
6C |
21 |
| Code (dez.) | 72 | 97 | 108 | 108 | 111 | 44 | 32 | 75 | 105 | 101 | 108 | 33 |
Steuerzeichen
Historisch gesehen baut ASCII auf Zeichencodierungen für Fernschreiber (engl. teletype writer) auf, beispielsweise dem Baudot-Code und insbesondere dem Murray-Code, die wiederum auf Zeichencodierungen für frühere Telegrafen wie dem Morse-Code basieren.
Die ersten 32 Zeichen und das letzte Zeichen im ASCII-Code sind Steuerzeichen für das Ausgabegerät und werden nicht als sichtbare Symbole im Text dargestellt. Diese Steuerzeichen sind historisch durch ihre Verwendung für Fernschreiber begründet, was sich auch an ihren Bezeichnungen erkennen lässt (z. B. “Zeilenvorschub”, “Wagenrücklauf”). Viele dieser Zeichen haben heute in Textdateien keine Bedeutung mehr und können hier ignoriert werden. Für uns sind im Wesentlichen nur die folgenden Steuerzeichen relevant:
Das Tabulator-Zeichen (engl. horizontal tabulator, kurz HT) mit dem Hexadezimal-Code 09 (dez. 9) wird insbesondere in Textdateien verwendet, die Tabellendaten beschreiben, um Daten in einer Zeile voneinander zu trennen. Das Zeichen wird in den meisten Textverarbeitungsprogrammen mit der Tabulator-Taste erzeugt und durch mehrere aufeinanderfolgende Leerzeichen angezeigt.
Ein Zeilenumbruch, der in Textverarbeitungsprogrammen mit der Eingabe-Taste erzeugt wird, wird je nach Betriebssystem unterschiedlich codiert:
- In Linux, iOS und anderen Unix-ähnlichen Betriebssystemen wird das Zeilenvorschub-Zeichen (engl. line feed, kurz LF) mit dem Hexadezimal-Code
0A(dez. 10) für einen Zeilenumbruch verwendet. - In Windows steht vor dem Zeilenvorschub-Zeichen zusätzlich das Wagenrücklauf-Zeichen (engl. carriage return, kurz CR) mit dem Hexadezimal-Code
0D(dez. 13), so dass ein Zeilenumbruch hier immer durch zwei aufeinanderfolgende Bytes repräsentiert wird (hex.0D 0A).
Erweitertes ASCII
Der ASCII-Zeichensatz wurde ursprünglich nur zur Codierung englischsprachiger Texte entwickelt und enthält daher keinerlei regionale Sonderzeichen wie beispielweise die deutschen Umlaute, das Eszett oder Vokale mit Akzenten – von Buchstaben anderer Alphabete ganz abgesehen.
Aus diesem Grund wurden ab Ende der 1970er verschiedene Standards für Erweiterungen des ASCII-Zeichensatzes veröffentlicht, in denen die übrigen 128 Zeichen, die bei einer 8-Bit-Codierung festgelegt werden können, für verschiedene regionale Schriftsysteme festgelegt wurden. Die bekanntesten dieser Erweiterungen sind zum einen die ISO 8859-Codierungen, zum anderen die Windows Codepages, deren jeweilige Varianten für westeuropäische Sprachen (ISO 8859-1 und Windows-1252) zum Teil auch heute noch (wenn auch im Vergleich zu Unicode in sehr viel geringerem Maße) verwendet werden. Wir betrachten diese beiden Zeichencodierungen hier hauptsächlich deswegen, weil Unicode auf ihnen aufbaut.
ISO 8859-1
Die Normenfamilie ISO 8859 definiert verschiedene 8-Bit-Zeichencodierungen, die den ASCII-Zeichensatz um Sonderzeichen erweitern. Hier werden nur Symbole für die Codepoints 160–255 (hex. A0–FF) definiert, die Codepoints 128–159 (hex. 80–9F) werden nicht festgelegt. Die Normenfamilie umfasst Standards für verschiedene Schriftsysteme (neben Lateinisch z. B. Arabisch, Griechich, Kyrillisch), die als ISO 8859-1 bis 8859-16 bezeichnet sind.
ISO 8859-1 (auch als Latin-1 bezeichnet) ist dabei die Zeichencodierung für westeuropäische Sprachen und die am weitesten verbreitete Variante der ISO 8859-Normen.1
Die folgende Tabelle stellt die zusätzlichen Zeichen im ISO 8859-1-Zeichensatz dar:
| Code (hex.) | …0 | …1 | …2 | …3 | …4 | …5 | …6 | …7 | …8 | …9 | …A | …B | …C | …D | …E | …F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A… | NBSP | ¡ | ¢ | £ | ¤ | ¥ | ¦ | § | ¨ | © | ª | « | ¬ | SHY | ® | ¯ |
| B… | ° | ± | ² | ³ | ´ | µ | ¶ | · | ¸ | ¹ | º | » | ¼ | ½ | ¾ | ¿ |
| C… | À | Á | Â | Ã | Ä | Å | Æ | Ç | È | É | Ê | Ë | Ì | Í | Î | Ï |
| D… | Ð | Ñ | Ò | Ó | Ô | Õ | Ö | × | Ø | Ù | Ú | Û | Ü | Ý | Þ | ß |
| E… | à | á | â | ã | ä | å | æ | ç | è | é | ê | ë | ì | í | î | ï |
| F… | ð | ñ | ò | ó | ô | õ | ö | ÷ | ø | ù | ú | û | ü | ý | þ | ÿ |
Hier werden zwei weitere gebräuchliche Steuerzeichen definiert:
- Das Zeichen NBSP mit dem Hexadezimal-Code
A0(dezimal 160) stellt das geschützte Leerzeichen (engl. non-breaking space) dar. - Das Zeichen SHY mit dem Hexadezimal-Code
AD(dezimal 173) ist das weiche Trennzeichen (engl. soft hyphen).
Beispiel:
Die Zeichenfolge “Grüße aus Mölln!” wird in ISO 8859-1 durch die Bytefolge 47 72 FC DF 65 20 61 75 73 20 4D F6 6C 6C 6E 21 (hexadezimal) repräsentiert.
| Zeichen | G | r | ü | ß | e | a | u | s | M | ö | l | l | n | ! | ||
| Code (hex.) | 47 |
72 |
FC |
DF |
65 |
20 |
61 |
75 |
73 |
20 |
4D |
F6 |
6C |
6C |
6E |
21 |
| Code (dez.) | 71 | 114 | 252 | 223 | 101 | 32 | 97 | 117 | 115 | 32 | 77 | 246 | 108 | 108 | 110 |
Windows-1252 (ANSI)
Die von Microsoft für das Betriebssystem Windows entwickelten Windows Codepages definieren alternative ASCII-Erweiterungen, die zu großen Teilen identisch mit den ISO 8859-Standards sind. Das Äquivalent zu ISO 8859-1 ist Windows-1252 (auch Codepage 1252 oder Western European). Diese Zeichencodierung wird auch oft ANSI-Zeichencode genannt (ANSI steht für American National Standards Institute).2
Windows-1252 unterscheidet sich von ISO 8859-1 nur darin, dass hier auch druckbare Symbole für die meisten der Codepoints 128–159 (hex. 80–9F) festlegt werden:
| Code (hex.) | …0 | …1 | …2 | …3 | …4 | …5 | …6 | …7 | …8 | …9 | …A | …B | …C | …D | …E | …F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8… | € | ‚ | ƒ | „ | … | † | ‡ | ˆ | ‰ | Š | ‹ | Œ | Ž | |||
| 9… | ‘ | ’ | “ | ” | • | – | — | ˜ | ™ | š | › | œ | ž | Ÿ |
Auf diese Weise entstand eine Vielzahl unterschiedlicher Zeichencodierungen für verschiedene Alphabete, in denen dasselbe 8-Bit-Muster je nach Kontext verschiedene Zeichen bedeuten kann. Neben 8-Bit-Zeichencodierungen entstanden dabei auch Codierungen, die mehr Bits pro Zeichen verwenden, um alle relevanten Zeichen zu codieren, etwa für das chinesische oder japanische Schriftsystem.
Unicode
Der Unicode-Zeichensatz wurde entwickelt, um dem Chaos aus regionalspezifischen Codierungen ein Ende zu bereiten und alle Zeichen in einem Standard zusammenzufassen. Unicode (auch ISO 10646 oder UIC, kurz für Universal Coded Character Set) ist heute der mit Abstand am weitesten verbreitete internationale Standard zur Definition eines global einheitlichen Zeichensatzes.
Ziel des Unicode-Standards ist es, langfristig für jedes Symbol aller weltweit bekannten Schrift- und Zeichensysteme einen Codepoint (“Unicode-Nummer”) festzulegen. Der aktuelle Unicode-Standard (Version 13.0.0, Stand August 2021) umfasst 143 859 Zeichen, darunter neben Schriftzeichen und Währungssymbolen auch geometrische Symbole und Emojis.3
Die ersten 256 Codepoints sind in Unicode identisch mit ASCII und ISO 8859-1 bzw. ANSI (bis auf die Codepoints 128–159, für die in Unicode keine druckbaren Symbole definiert sind, sondern weitere Steuerzeichen).
Da ein Byte hier klarerweise nicht mehr ausreicht, um ein Unicode-Zeichen darzustellen, gibt es verschiedene Standards zur Zeichencodierung, also um die Unicode-Nummern als Byte-Codes darzustellen. Verfahren zur Abbildung von Unicode-Nummern auf Byte-Codes werden als UTF (Unicode Transformation Format) bezeichnet.
UTF-32
Die einfachste, aber auch speicheraufwendigste Methode besteht darin, jedes Unicode-Zeichen mit vier Byte (= 32 Bit) darzustellen, so dass bis zu 232 (also mehr als 4 Mrd.) Zeichen darstellbar sind. Diese Zeichencodierung wird als UTF-32 bezeichnet. Eine UTF-32-codierte Textdatei ist also viermal so groß wie eine mit ANSI oder ISO 8859-1 codierte Datei, auch wenn nur Zeichen aus dem ANSI- bzw. ISO 8859-1-Zeichensatz verwendet werden.
Beispiel:
Die Zeichenfolge “Grüße aus Mölln!” wird in ANSI und ISO 8859-1 durch die Bytefolge 47 72 FC DF 65 20 61 75 73 20 4D F6 6C 6C 6E 21 (hexadezimal) repräsentiert, also durch 16 Byte. Wird UTF-32-Codierung verwendet, werden 64 Byte benötigt, nämlich 00 00 00 47 00 00 00 72 00 00 00 FC 00 00 00 DF…
UTF-8
Eine bessere Methode besteht darin, variable Codelängen zu verwenden – die Zeichencodierung UTF-8 setzt eine solche Strategie um. UTF-8 ist momentan die mit Abstand am weitesten verbreitete Zeichencodierung für Unicode-Textdateien.4
Hier werden häufiger auftretende Zeichen (geringere Unicode-Nummern) mit weniger Byte codiert als spezielle, seltenere Zeichen (höhere Unicode-Nummern). Das Codierungsverfahren ist folgendermaßen definiert:
- Beginnt ein Byte mit dem höchsten Bit 0, so codieren die restlichen 7 Bit das entsprechende ASCII-Zeichen.
0xxx xxxx - Beginnt ein Byte dagegen mit der Bitfolge 110, so wird es zusammen mit dem folgenden Byte als Unicode-Zeichen interpretiert. Dabei wird erwartet, dass das folgende Byte mit der Bitfolge 10 beginnt (anderenfalls ist der UTF-8-Code nicht “wohlgeformt”, also bzgl. der Syntaxregeln für UTF-8-Codes formal nicht korrekt). Der Codepoint des Unicode-Zeichens wird durch die letzten 5 Bit des ersten Zeichens und die letzten 6 Bit des zweiten Zeichens gebildet. Auf diese Weise werden mit 11 Bit die Unicode-Zeichen mit den Nummern 128 bis 2047 dargestellt (u. a. Lateinisch, Griechisch, Kyrillisch, Arabisch und Hebräisch).
110x xxxx 10xx xxxx - Beginnt es mit der Bitfolge 1110, wird es mit den beiden folgenden Byte zusammen als Unicode-Zeichen interpretiert. Auf diese Weise werden mit 16 Bit die Unicode-Zeichen mit den Nummern 2048 bis 65 535 dargestellt (u. a. Pfeile, mathematische Symbole, Chinesisch, Japanisch).
1110 xxxx 10xx xxxx 10xx xxxx - Beginnt es mit 11110, wird es mit den folgenden drei Bytes zusammen als Unicode-Zeichen interpretiert. Auf diese Weise werden mit 21 Bit die Unicode-Zeichen mit den Nummern 65 536 bis 2 097 151 dargestellt (u. a. antike Schriftzeichen, Emojis).
1111 0xxx 10xx xxxx 10xx xxxx 10xx xxxx
Ein Unicode-Zeichen wird in UTF-8 also durch ein bis vier Bytes repräsentiert, wobei gewährleistet ist, dass über 2 Mio. Zeichen darstellbar sind (von denen momentan knapp 7% genutzt werden).
Beispiele:
- Das Unicode-Zeichen Ä hat die Unicode-Nummer
C4(hex.) bzw. 196 (dez.), die Binärdarstellung dieser Zahl ist 1100 0100.
Die UTF-8-Codierung benötigt also 2 Byte und lautet: 1100 0011 1000 0100 (binär) bzw.C3 84(hex.). - Das Unicode-Zeichen 😀 hat die Unicode-Nummer
1F600(hex.) bzw. 128 512 (dez.), die Binärdarstellung dieser Zahl ist 1 1111 0110 0000 0000.
Die UTF-8-Codierung benötigt also 4 Byte und lautet: 1111 0000 1001 1111 1001 1000 1000 0000 (binär) bzw.F0 9F 98 80(hex.).
Für Textdateien sollte in der Regel immer UTF-8 als Zeichencodierung verwendet werden, sofern Sonderzeichen verwendet werden, die über den ASCII-Zeichensatz hinaus gehen, da dieses Format am gebräuchlichsten ist.
Übungsaufgaben
Aufgabe 1: Zeichencodierung
In einer Textdatei, die im Textbearbeitungsprogramm (fälschlicherweise) mit der Zeichencodierung ISO 8859-1 angezeigt wird, kommt mehrmals die Zeichenfolge ä vor.
- Welchen Bitcode hat die Zeichenfolge ä in ISO 8859-1?
- Welche Zeichencodierung ist vermutlich eigentlich richtig für diese Textdatei?
- Welches Zeichen wird statt ä in der eigentlich richtigen Zeichencodierung dargestellt?
Aufgabe 2: Textdateigröße
Der folgende Text soll als erweiterter ASCII-Code dargestellt werden (ISO 8859-1 oder Windows-1252/ANSI):
Bei UTF-8 werden
1-4 Byte verwendet,
um ein Zeichen zu
speichern.
- Wie viele Bytes werden zur Darstellung des Textes benötigt?
- Überprüfen Sie Ihre Vorhersage, indem Sie den Text in einen Texteditor eingeben/kopieren, als Textdatei in einem geeigneten Format (ISO 8859-1 oder Windows-1252/ANSI) speichern und anschließend die Dateigröße überprüfen.
- Macht es für die Dateigröße einen Unterschied, ob Sie die Textdatei in Windows oder Linux erstellen?
- Ändert sich die Dateigröße, wenn der Text mit UTF-8 codiert wird?
Aufgabe 3: UTF-8-Codierung
Welches Unicode-Zeichen verbirgt sich hinter dem (hier hexadezimal dargestellten) UTF-8-Code F0 9F 91 8D?
Ermitteln Sie dazu seine Unicode-Nummer aus dem Bitcode und suchen Sie in der Unicode-Zeichentabelle auf https://unicode-table.com/de danach (im Suchfeld oben die Unicode-Nummer als Hexadezimal- oder Dezimalzahl angeben).
-
Der später eingeführte Standard ISO 8859-15 (auch Latin-9) für westeuropäische Sprachen unterscheidet sich nur in 8 Zeichen von ISO 8859-1 (Latin-1):
↩︎Code (hexadezimal) A4A6A8B4B8BCBDBEZeichen in ISO 8859-1 € Š š Ž ž Œ œ Ÿ Zeichen in ISO 8859-15 ¤ ¦ ¨ ´ ¸ ¼ ½ ¾ -
Genauer formuliert: Windows-1252 basiert auf einem früheren Entwurf der ANSI-Zeichencodierung, die später mit Änderungen für die Codepoints 128–159 zu ISO 8859-1 wurde. Die Bezeichnung “ANSI” wird heute aber überwiegend synonym für Windows-1252 verwendet. ↩︎
-
siehe offizielle Website des Unicode-Konsortiums: https://home.unicode.org ↩︎
-
So verwenden 2021 über 97% aller Webseiten UTF-8 als Zeichencodierung, siehe https://w3techs.com/technologies/cross/character_encoding/ranking ↩︎
2.2.2 Codierung von Bilddaten
In dieser Lektion werden wir uns mit den Grundlagen der Binärdarstellung von Bildern als Rastergrafiken beschäftigen, Merkmale von Rastergrafiken sowie einfache Dateiformate für Rastergrafiken kennenlernen.
Rastergrafiken eignen sich gut als anschauliches und aus dem Alltag bekanntes Beispiel zur Vertiefung des Themas “Codierung” im Schulunterricht, weil sie sich zum einen vergleichsweise einfach codieren und repräsentieren lassen, dabei zum anderen aber auch Diskussionsspielraum offen lassen. Die Codierung von Bilddaten motiviert außerdem die Notwendigkeit, Daten zu komprimieren, was augenscheinlich wird, wenn der Datenumfang von Bildern untersucht und bewertet wird.
Rastergrafiken
Wenn Sie eine Bilddatei in einem Format wie JPG oder PNG in einem Bildanzeigeprogramm öffnen und stark vergrößern, erkennen Sie, dass das Bild aus einzelnen quadratischen Bildpunkten zusammengesetzt ist, die in einem Raster angeordnet sind. Aus diesem Grund wird dieses Bildformat als Rastergrafik bezeichnet.

Eine Rastergrafik beschreibt also Bilddaten in digitaler Form, indem das Bild in ein Raster von Bildpunkten, die sogenannten Pixel (kurz für engl. pixel elements), aufgeteilt wird und jedem Pixel ein diskreter Farbwert zugeordnet wird. Die wichtigsten Attribute einer Rastergrafik sind die Bildgröße, also Breite und Höhe (in Pixeln), sowie die Farbtiefe, also die Anzahl an Bits, die benötigt werden, um den Wert eines Pixels darzustellen. Wird beispielsweise nur 1 Bit pro Pixel verwendet, lassen sich nur 2 verschiedene Farbwerte pro Pixel unterscheiden (z. B. schwarz und weiß), während sich mit 8 Bit (also 1 Byte) bereits 28 = 256 verschiedene Farbwerte darstellen lassen.
Struktur
Die Pixelwerte werden im Speicher üblicherweise zeilenweise von oben links nach unten rechts als Bitfolge repräsentiert. Dabei codieren jeweils D aufeinanderfolgende Bits den Wert eines Pixels, wobei D die Farbtiefe darstellt (z. B. 8 Bit pro Pixel). Bei einer Farbtiefe von D Bit kann jedes Pixel 2D verschiedene Farbwerte annehmen.
Beispiel: Ein Bild der Größe 8 × 8 Pixel, die jeweils nur schwarz oder weiß sind, lässt sich als Bitfolge der Länge 64 Bit darstellen. Jedes Bit stellt ein Pixel dar (hier: 0 = weiß, 1 = schwarz).
Der Datenumfang einer Rastergrafik der Größe W × H Pixel (W ist die Breite und H die Höhe) mit einer Farbtiefe von D Bit pro Pixel umfasst somit W⋅H⋅D Bit, wenn die Daten unkomprimiert vorliegen.
Wenn die Größe und Farbtiefe des Bildes nicht fest vorgegeben ist, müssen diese Informationen zusammen mit den Bilddaten gespeichert werden, damit die Bilddaten richtig interpretiert werden können.
Farbwerte
Wir unterscheiden Bilder nach den Werten, die ihre Pixel annehmen können, als Schwarz-Weiß-Bilder (Binärbilder), Graustufenbilder und Farbbilder.
| In einem Binärbild kann jedes Pixel nur einen von zwei Werten annehmen, die üblicherweise als schwarz oder weiß dargestellt werden (“Schwarz-Weiß-Bild”). In diesem Fall reicht ein Bit pro Pixel, um die Bilddaten binär darzustellen (Farbtiefe D = 1). Bei Binärbildern repräsentiert 0 in der Regel ein Hintergrundpixel (hier weiß dargestellt) und 1 ein Vordergrundpixel (hier schwarz dargestellt). | |
| In Graustufenbildern kann ein Pixel dagegen verschiedene Graustufen als Wert haben. Wird jedes Pixel durch 1 Byte (= 8 Bit) repräsentiert, bedeutet das etwa, dass 28 = 256 verschiedene Graustufen im Bild vorkommen können. Der Wert 0 repräsentiert dabei schwarz, 255 weiß und die Werte 1 bis 254 in linearer Abstufung die dazwischen liegenden Grautöne. | |
| In Farbbildern wird pro Pixel üblicherweise ein Rot-, Grün- und Blauwert gespeichert (RGB-Werte). Mit diesen drei Werten lassen sich alle Farben des RGB-Farbraums darstellen, in dem durch das additive Mischen der drei Grundfarben Rot, Grün und Blau jeder beliebige Farbeindruck nachgebildet wird. Gelb ergibt sich beispielsweise durch 100% Rot + 100% Grün + 0% Blau, während 50% Rot + 75% Grün + 100% Blau ein Himmelblau ergibt. Alternativ kann auch ein “Farbpalette” verwenden werden zur Repräsentation von Bildern mit mehreren Farben verwendet werden (siehe unten). |
RGB-Farbwerte
Wird für den Rot-, Grün- und Blauwert je 1 Byte verwendet, ergibt sich eine Farbtiefe von 3 Byte bzw. 24 Bit, womit insgesamt (28)3 = 224 ≈ 16 Mio. verschiedene Farben pro Pixel darstellbar sind. Diese Werte liegen im Speicher in der Regel direkt aufeinanderfolgend in der Reihenfolge RGB (seltener auch in anderen Reihenfolgen wie BGR) und können als Hexadezimalcode mit sechs Ziffern (für 3 Byte) dargestellt werden:
Die hexadezimale Farbdarstellung wird sehr häufig in Grafikprogrammen oder auch in Webseiten zur Definition von Farben verwendet. Daneben ist aber auch die Darstellung durch drei RGB-Werte aus dem Bereich 0–255 oder 0–100% üblich.
Beispiel:
Der Hexadezimalcode 80BEFF entspricht den dezimalen RGB-Farbwerten 128, 190, 255, bzw. als Prozentangaben bzgl. 255 als Maximalwert 50.2%, 74.5% und 100%.
Tool: In dieser interaktiven Anzeige können Sie verschiedene Farben über ihre RGB-Werte (8 Bit pro Kanal) zusammenmischen. Das untere Feld zeigt den RGB-Farbcode der resultierenden Farbe (in der Mitte der drei Kreise) im Hexadezimalformat an.
Farbkanäle
Jedes Pixel in einem RGB-Farbbild der Farbtiefe 3⋅D enthält also im Grunde drei Helligkeitswerte, nämlich jeweils einen D-Bit-Wert für Rot, Grün und Blau. Die eigentliche Farbe des Pixels entsteht durch die Kombination dieser drei Werte. Ein Farbbild lässt sich also auch durch drei Bilder repräsentieren, bei denen jedes Pixel nur je einen D-Bit-Wert hat, nämlich entweder den Rot-Wert, Grün-Wert oder Blau-Wert des Farbbildes. Die so repräsentierten Bilder werden als Farbkanäle bezeichnet.
 |
 |
 |
 |
RGB-Farbbild |
Darstellung des Rot-Kanals |
Darstellung des Grün-Kanals |
Darstellung des Blau-Kanals |
Ein RGB-Bild wird dementsprechend auch als Mehrkanal-Bild bezeichnet, das sich aus dem Rot-, Grün- und Blaukanal zusammensetzt, während ein Graustufenbild (bzw. auch ein Binärbild) ein Einkanal-Bild ist. Die Farbtiefe wird bei Farbbildern oft auch pro Kanal angegeben, also “8-Bit pro Kanal” statt “24-Bit”.
In den getrennten Darstellungen der Kanäle lässt sich gut erkennen, welche Farbe aus welchen Rot-, Grün- und Blau-Anteilen zusammengesetzt ist: Die gelben Bildbereiche auf dem Leuchtturm enthalten hohe Anteile Rot und Grün, aber kaum Blau, während die hellen himmelblauen Bereiche im Hintergrund hohe Grün-/Blau-Anteile und einen etwas geringeren Rot-Anteil enthalten.
Alphakanal
Um Bildbereiche mit Abstufungen transparent – also mehr oder weniger durchsichtig – darzustellen, kann ein zusätzlicher Kanal verwendet werden, der für jedes Pixel einen Transparenzwert enthält. Dieser zusätzliche Kanal wird als Alphakanal bezeichnet.1 Jedes Pixel in einem Farbbild mit Transparenz enthält dann vier Helligkeitswerte, je einen für Rot, Grün, Blau und “Undurchsichtigkeit” (Alpha-Wert), die auch als RGBA-Werte bezeichnet werden. Bei einem RGBA-Bild mit 8 Bit pro Kanal bedeutet ein Alpha-Wert 0 in der Regel, dass das Pixel vollständig transparent ist (also unsichtbar), während 255 ein vollständig undurchsichtiges Pixel kennzeichnet.
 |
 |
 |
Darstellung der RGB-Kanäle |
Darstellung des Alpha-Kanals |
Anzeige des RGBA-Farbbild über einem gemusterten Hintergrund |
Farbpaletten
Enthält ein Bild nur eine geringe Anzahl von Farben (z. B. nur schwarz, weiß, gelb und rot), können die Farben alternativ auch in Form einer Farbpalette repräsentiert werden. Die Farbpalette gibt eine begrenzte Menge von Farben vor, und in jedem Pixel wird nun statt Farbwert die Nummer der entsprechenden Farbe gespeichert.2 Bei einer Farbpalette mit 4 Einträgen reichen dazu beispielsweise 2 Bit pro Pixel.
Die Paletteninformation – also die Anzahl der Paletteneinträge und der RGB-Farbwert für jeden Eintrag – müssen mit den Bilddaten zusammen gespeichert werden, damit aus den Daten entnommen werden kann, welche Nummer welche Farbe darstellt.
Dateiformate
Damit Bilddaten gespeichert und interpretiert werden können, wird in einem Dateiformat genau festgelegt, welche Informationen in welcher Codierung an welcher Stelle in der Datei stehen. Ein Datenformat legt also Syntax und Semantik fest. Um ein Dateiformat zu spezifizieren müssen die folgenden Fragen berücksichtigt werden:
- Was muss alles gespeichert werden? Dazu gehören bei Rastergrafiken beispielsweise die folgenden Informationen:
- Wie groß ist das Bild? (Höhe, Breite)
- Wie viele Bits werden pro Pixelwert verwendet? (Farbtiefe)
- Wie ist ein Pixelwert zu interpretieren? (Schwarz-Weiß-Werte, Grauwerte, RGB-Farbwerte)
- ggf. Kommentare und weitere Informationen über das Bild (z. B. Autor*in, Lizenz)
- die eigentlichen Bilddaten (Pixelwerte)
- In welcher Form wird es gespeichert (Syntax)?
- Wo stehen welche Daten? (Struktur des Headers, Reihenfolge der Pixelwerte)
- Wie sind welche Daten codiert? (Textformat, Binärformat)
Examplarisch werden wir hier Portable Anymap (kurz PNM) als ein sehr einfaches Dateiformat für Rastergrafiken vorstellen und anhand dessen grundlegende Merkmale von Dateiformaten für Rastergrafiken veranschaulichen.
Portable Anymap
PNM (kurz für Portable Anymap) ist ein sehr einfaches, unkomprimiertes Dateiformat für Binär-, Graustufen und Farbbilder, in dem sich Bilder auch als reine Textdateien speichern lassen. PNM eignet sich daher gut als Einstiegsbeispiel für Bilddateiformate.
PNM lässt sich für Binärbilder, Graustufenbilder und RGB-Farbbilder (ohne Transparenz) mit 8 Bit oder 16 Bit Farbtiefe verwenden.3 Es wird von vielen (aber längst nicht allen) modernen Grafikprogrammen (z. B. GIMP) und Bildbetrachtern unterstützt.
Das PNM-Format für Binärbilder heißt Portable Bitmap (PBM), Portable Graymap (PGM) für Graustufenbilder und Portable Pixmap (PPM) für Farbbilder.4 Die Abkürzungen werden üblicherweise auch als Dateiendungen für die Formate (.pbm, .pgm, .ppm) verwendet. PNM erlaubt es, die Bilddaten im Binärformat, aber auch als reine Textdatei im ASCII-Format zu speichern. Dadurch lassen sich PNM-Dateien prinzipiell auch mit einem einfachen Texteditor erstellen und bearbeiten – allerdings so nicht als Bild anzeigen.
Tool: Wenn auf Ihrem Rechner kein Grafikprogramm oder Bildbetrachter installiert ist, mit dem Sie PNM-Dateien als Bild darstellen können, können Sie alternativ diesen einfachen Online-Bildbetrachter für PNM-Dateien verwenden:
Dateistruktur
PNM definiert sechs Bildformate: PBM, PGM und PPM, jeweils mit Bilddaten im Binärformat oder im Textformat. Die Formate sind alle nach dem selben Schema aufgebaut, das anhand des folgenden Beispiels erläutert wird ( Download):
P2
17 8
100
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 50 10 50 10 10 10 10 10 80 10 80 10 10 10 10 10
10 50 10 50 10 65 65 65 10 80 10 80 10 10 10 10 10
10 50 50 50 10 10 10 65 10 80 10 80 10 95 95 95 10
10 50 10 50 10 65 65 65 10 80 10 80 10 95 10 95 10
10 50 10 50 10 65 10 65 10 80 10 80 10 95 10 95 10
10 50 10 50 10 65 65 65 10 80 10 80 10 95 95 95 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
Die ersten drei Zeilen stellen den Dateikopf oder Header dar, der Informationen über das Bildformat enthält, anschließend folgen die Pixelwerte, also die eigentlichen Bilddaten.
P2 |
Die “Magic Number” zu Beginn codiert den Bildtyp (Binär-, Graustufen- oder Farbbild) und das Format, in dem die Bilddaten gespeichert sind (binär oder im ASCII-Textformat). “P2” bedeutet “Graustufenbild im ASCII-Textformat”. |
17 8 |
Es folgt die Breite und Höhe des Bildes in Pixeln, hier also 17 × 8 Pixel. |
100 |
Bei Graustufen- und Farbbildern folgt der Wert, der 100% Helligkeit entspricht (max. 65536). Da hier 100 steht, stehen in den folgenden Bilddaten nur Werte zwischen 0 und 100. |
10 ... |
Nach dem Header folgen die eigentlichen Bilddaten, entweder als Dezimalzahlen im ASCII-Textformat oder binär codiert. |
Der Header ist immer im ASCII-Textformat gespeichert, Breite, Höhe und max. Helligkeit sind hier als Dezimalzahlen angegeben. Die einzelnen Werte können durch beliebig viele Leerzeichen, Zeilenumbrüche oder Tabulatorzeichen voneinander getrennt sein.5
Auf den letzten Eintrag des Headers folgen die eigentlichen Bilddaten, je nach “Magic Number” entweder als Dezimalzahlen im ASCII-Format (jeweils durch Leerzeichen, Tabulatorzeichen oder Zeilenumbrüche getrennt) oder binär codiert.
- Bei Schwarz-Weiß-Bildern kommen hier nur 0 und 1 als Werte vor, wobei 0 in der Regel als weiß und 1 als schwarz interpretiert wird.
- Bei Graustufen- und Farbbildern kommen hier nur Werte zwischen 0 und M vor, wobei M der maximale Helligkeitswert ist, der nach der Breite und Höhe im Header steht. In einem Graustufenbild wird 0 als schwarz, M als weiß und 1 bis M-1 als Graustufen dazwischen interpretiert.
Das in diesem Beispiel codierte Bild lässt sich in der Textdarstellung eventuell erahnen und ist hier in 10-facher Vergrößerung dargestellt:

Bildformate
Portable Anymap bietet die folgenden Bildformate an, die durch die “Magic Number” im Header festgelegt werden:
| Magic Number | Bildtyp | Formatname | Codierung der Bilddaten | Bits/Pixel (Binärformat) | Beispieldatei |
|---|---|---|---|---|---|
| P1 | Binärbild | Portable Bitmap (PBM) | ASCII-Textformat | Download | |
| P2 | Graustufenbild | Portable Graymap (PGM) | ASCII-Textformat | Download | |
| P3 | RGB-Farbbild | Portable Pixmap (PPM) | ASCII-Textformat | Download | |
| P4 | Binärbild | Portable Bitmap (PBM) | Binärformat | 1 | Download |
| P5 | Graustufenbild | Portable Graymap (PGM) | Binärformat | 8 oder 16 | Download |
| P6 | RGB-Farbbild | Portable Pixmap (PPM) | Binärformat | 24 oder 48 | Download |
Ob es sich um ein Binärbild, Graustufenbild oder Farbbild handelt, wird ausschließlich anhand der “Magic Number” entschieden, nicht anhand der Dateiendung! Eine Bilddatei im Portable Anymap-Format mit der Dateiendung .ppm, das zu Beginn den Eintrag P2 enthält, wird also als Graustufenbild (PGM) interpretiert, nicht als Farbbild (PPM)!
Wenn die Bilddaten im Binärformat codiert werden, gilt:
- Bei Schwarz-Weiß-Bildern werden je 8 Pixelwerte pro Byte gespeichert (1 Bit pro Pixel).
- Bei Graustufenbildern werden je 1–2 Byte pro Pixel gespeichert, bei RGB-Farbbildern je 1–2 Bytes pro Farbkanal (also 3–6 Byte pro Pixel). Die Anzahl an Bytes wird hier aus dem maximalen Helligkeitswert abgeleitet: Ist der Wert kleiner als 256, wird 1 Byte verwendet, anderenfalls 2 Byte.
Im Beispiel wird 100 als maximaler Helligkeitswert verwendet, hier werden die Bilddaten also mit Farbwerten zwischen 0 (schwarz) und 100 (weiß) angegeben. Würden die Bilddaten im Binärformat codiert werden (“Magic Number” P5), würde hier aus technischen Gründen 1 Byte pro Pixel verwendet werden – auch wenn 7 Bit prinzipiell ausreichen, um die Werte 0 – 100 zu codieren. In der Praxis ist es am üblichsten, in Portable Anymap-Dateien als maximalen Helligkeitswert 255 anzugeben. So können 256 Graustufen bzw. 24-Bit RGB-Werte als Farbwerte gespeichert werden (8 Bit/Kanal). Der maximale Helligkeitswert 65535 (= 16 Bit/Kanal) ist eher unüblich, da er von den meisten Anzeigegeräten nicht sinnvoll dargestellt werden kann.
Beispiele
In der Bildformat-Tabelle finden Sie für jedes Format P1–P6 eine Datei als Beispiel verlinkt. Im folgenden sehen wir uns den Dateiinhalt dieser Dateien genauer an und interpretieren den Inhalt.
Binärbild
 Die Dateien smiley_ascii.pbm und smiley_binary.pbm stellen ein Schwarz-Weiß-Bild dar. Der Header ist bis auf die “Magic Number” identisch. In der ersten Datei stehen nach dem Header die Pixelwerte im Textformat, durch Leerzeichen und Zeilenumbrüche getrennt, so dass sich in einem Texteditor gut erkennen lässt, wie das Bild aussieht.
Die Dateien smiley_ascii.pbm und smiley_binary.pbm stellen ein Schwarz-Weiß-Bild dar. Der Header ist bis auf die “Magic Number” identisch. In der ersten Datei stehen nach dem Header die Pixelwerte im Textformat, durch Leerzeichen und Zeilenumbrüche getrennt, so dass sich in einem Texteditor gut erkennen lässt, wie das Bild aussieht.
P1
8 8
0 0 1 1 1 1 0 0
0 1 0 1 1 0 1 0
1 1 0 1 1 0 1 1
1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 1
1 1 0 0 0 0 1 1
0 1 1 0 0 1 1 0
0 0 1 1 1 1 0 0
P4
8 8
<ZÛÿ.Ãf<
In der zweiten Datei steht zu Beginn P4 statt P1, was bedeutet, dass die auf den Header folgenden Pixelwerte binär codiert sind. Wenn Sie diese Datei in einem Texteditor öffnen, sehen Sie nach dem Header nur acht unverständliche Zeichen: <ZÛÿ.Ãf< (. steht hier für ein nicht druckbares Zeichen).
Das liegt daran, dass der Texteditor versucht, die folgenden Zeichen ebenfalls als Textzeichen im ASCII-Format zu interpretieren – in Wirklichkeit stehen hier aber die binär codierten Pixelwerte. Wenn Sie diese acht Byte-Werte dagegen als Binärzahlen darstellen, wird der Inhalt etwas klarer:
00111100 01011010 11011011 11111111 10000001 11000011 01100110 00111100
Wenn Sie diese Bitfolge zeilenweise aufschreiben (je 8 Bit pro Zeile, da das Bild 8 Pixel breit ist), lässt sich der Bildinhalt darin wieder erkennen (zur besseren Sichtbarkeit sind 0-Bits hier heller dargestellt):
Graustufenbild
 Die Dateien smiley_ascii.pgm und smiley_binary.pgm stellen jeweils das gleiche Graustufenbild dar. Hier steht nach der Bildgröße im Header jeweils
Die Dateien smiley_ascii.pgm und smiley_binary.pgm stellen jeweils das gleiche Graustufenbild dar. Hier steht nach der Bildgröße im Header jeweils 255, das heißt, das die Pixelwerte 0–255 zur Darstellung der Graustufen verwendet werden. Auch hier lässt sich die ersten Datei in einem Texteditor einfach interpretieren: Die Pixelwerte stehen hier als Dezimalzahlen im Textformat, netterweise mit Leerzeichen und Zeilenumbrüchen so ausgerichtet, dass sich der Bildinhalt erkennen lässt:
P2
8 8
255
255 255 0 0 0 0 255 255
255 0 160 160 160 160 0 255
0 160 64 160 160 64 160 0
0 160 64 160 160 64 160 0
0 160 160 160 160 160 160 0
0 160 64 64 64 64 160 0
255 0 160 64 64 160 0 255
255 255 0 0 0 0 255 255
P5
8 8
255
ÿÿ....ÿÿÿ. .ÿ. @ @ .. @ @ .. .. @@@@ .ÿ. @@ .ÿÿÿ....ÿÿ
Wird die zweite Datei dagegen in einem Texteditor geöffnet, werden auch hier wieder nach dem Header 64 unverständliche Zeichen dargestellt, die durch die sinnlose Interpretation der binär codierten Grauwerte als ASCII-Zeichen entstehen. In einem Hexadezimal-Editor lässt sich dieser Teil sinnvoller interpretieren. Hier sind die Binärdaten hexadezimal dargestellt, wobei jedes Byte einen Grauwert zwischen 0 und 255 codiert (die Leerzeichen, Zeilenumbrüche und Farben dienen hier als Hilfestellung):
Farbbild
 Die Dateien smiley_ascii.ppm und smiley_binary.ppm stellen jeweils das gleiche RGB-Farbbild dar. Prinzipiell lassen sich diese Dateien genauso interpretieren wie die Graustufenbilder, nur stehen hier pro Pixel drei Werte – die Rot-, Grün- und Blau-Werte – direkt nacheinander, was das visuelle Interpretieren des eigentlichen Bildinhalts etwas erschwert. Es lassen sich aber zumindest die verschiedenen RGB-Werte erkennen, die im Bild vorhanden sind, z. B.
Die Dateien smiley_ascii.ppm und smiley_binary.ppm stellen jeweils das gleiche RGB-Farbbild dar. Prinzipiell lassen sich diese Dateien genauso interpretieren wie die Graustufenbilder, nur stehen hier pro Pixel drei Werte – die Rot-, Grün- und Blau-Werte – direkt nacheinander, was das visuelle Interpretieren des eigentlichen Bildinhalts etwas erschwert. Es lassen sich aber zumindest die verschiedenen RGB-Werte erkennen, die im Bild vorhanden sind, z. B. 255 255 255 (weiß), 127 94 0 (dunkles Gelb), usw.
P3
8 8
255
255 255 255 255 255 255 127 94 0 127 94 0 127 94 0 127 94 0 255 255 255 255 255 255
255 255 255 127 94 0 255 191 0 255 191 0 255 191 0 255 191 0 127 94 0 255 255 255
127 94 0 255 191 0 0 128 32 255 191 0 255 191 0 0 128 32 255 191 0 127 94 0
127 94 0 255 191 0 0 128 32 255 191 0 255 191 0 0 128 32 255 191 0 127 94 0
127 94 0 255 191 0 255 191 0 255 191 0 255 191 0 255 191 0 255 191 0 127 94 0
127 94 0 255 191 0 255 0 0 255 0 0 255 0 0 255 0 0 255 191 0 127 94 0
255 255 255 127 94 0 255 191 0 255 0 0 255 0 0 255 191 0 127 94 0 255 255 255
255 255 255 255 255 255 127 94 0 127 94 0 127 94 0 127 94 0 255 255 255 255 255 255
P6
8 8
255
ÿÿÿÿÿÿ.^..^..^..^.ÿÿÿÿÿÿÿÿÿ.^.ÿ¿.ÿ¿.ÿ¿.ÿ¿..^.ÿÿÿ.^.ÿ¿..€ ÿ¿.ÿ¿..€ ÿ¿..^..^.ÿ¿..€ ÿ¿.ÿ¿..€ ÿ¿..^..^.ÿ¿.ÿ¿.ÿ¿.ÿ¿.ÿ¿.ÿ¿..^..^.ÿ¿.ÿ..ÿ..ÿ..ÿ..ÿ¿..^.ÿÿÿ.^.ÿ¿.ÿ..ÿ..ÿ¿..^.ÿÿÿÿÿÿÿÿÿ.^..^..^..^.ÿÿÿÿÿÿ
Nach dem Header stehen 3·64 = 192 Zeichen, die in einem Texteditor durch willkürliche ASCII-Zeichen dargestellt werden und sich in der Hexadezimaldarstellung besser interpretieren lassen (hier wieder zur besseren Erkennbarkeit zeilenweise angeordnet und eingefärbt):
Speicheraufwand
Da die Bilddaten im PNM-Format nicht komprimiert werden, sind PNM-Dateien im Vergleich zu anderen Dateiformaten sehr groß: Für ein 8-Bit-Graustufenbild der Größe W × H Pixel werden im Binärdatenformat W ⋅ H Byte + ein paar Byte für den Header benötigt, für ein RGB-Bild die dreifache Menge. Ein Farbbild der Größe 4000 × 3000 Pixel (12 Megapixel) benötigt im PPM-Binärformat (“P6”) also ca. 36 MB an Speicher.
Im Textformat steigt der Speicherbedarf noch einmal um das Drei- bis Vierfache, da jeder Helligkeitswert hier nicht mit einem Byte, sondern mit 2–4 Byte (1–3 Dezimalziffern + Trennzeichen) gespeichert wird, so dass die Datei für ein 12-Megapixel-Farbbild im PPM-Textformat (“P3”) im schlimmsten Fall ca. 144 MB groß wird! Zum Vergleich: Eine JPEG- oder PNG-Datei derselben Bildgröße ist je nach Kompressionsgrad und Bildinhalt meistens nur etwa 4–16 MB groß.
Weitere Dateiformate
Abschließend finden Sie hier eine kurze Beschreibung weiterer bekannter Dateiformate für Rastergrafiken. Viele dieser Formate verwenden im Gegensatz zum PNM Datenkompression – dieses Thema werden wir im übernächsten Kapitel Datenkompression untersuchen.
| Name | Dateiendung | Beschreibung | |
|---|---|---|---|
| JPEG (kurz für Joint Photographic Experts Group) | .jpg, .jpeg | In JPEG-Dateien werden die Bilddaten nach der JPEG-Norm komprimiert. Die Kompression ist sehr effektiv, aber es geht ein Teil der Bildinformation dabei verloren (verlustbehaftete Kompression), allerdings so, dass die Unterschiede visuell in normaler Vergrößerung kaum auffallen (insbesondere bei Fotos). Der Kompressionsgrad und damit die Bildqualität kann beim Speichern gewählt werden. Da JPEG-Dateien durch die Kompression sehr klein sind, wird dieses Format speziell im Internet sehr häufig verwendet. | |
| PNG (kurz für Portable Network Graphics | .png | In PNG-Dateien werden die Bilddaten mit Methoden komprimiert, bei denen keine Bildinformation verloren geht (verlustfreie Kompression). Die Kompression funktioniert besonders gut, wenn die Bildern wenig Schattierungen, sondern eher gleichfarbige Linien und Flächen enthalten, also eher für Grafiken als für Fotos. Im Gegensatz zu JPG wird auch Transparenz unterstützt. PNG ist inzwischen im Internet relativ weit verbreitet. | |
| GIF (kurz für Graphics Interchange Format) | .gif | GIF ist ein Dateiformat für Bilder mit Farbpalette, das wie PNG verlustfreie Kompression verwendet. GIF-Dateien können auch mehrere Einzelbilder, die von Anzeigeprogrammen wie Webbrowern als Animationen abgespielt werden und sind daher im Internet ebenfalls sehr verbreitet. | |
| BMP (kurz für Windows Bitmap) | .bmp | BMP ist ein sehr bekanntes und einfaches Dateiformat für RGB-Bilder, in dem ein verlustfreies Kompressionsverfahren verwendet wird, das allerdings eher schwach ist. Dadurch sind die Dateien größer als etwa PNG-Dateien, weswegen BMP im Internet kaum verwendet wird. | |
| TIFF (kurz für Tagged Image File Format) | .tif | TIFF ist ein sehr flexibles Dateiformat, das ebenfalls in der Regel verlustfreie Kompression verwendet und Bilder mit hoher Qualität und Größe speichern kann. Die Dateien sind allerdings in der Regel sehr groß und finden daher im Internet kaum Verwendung, sondern vorwiegend im Printbereich. |
Übungsaufgaben
Aufgabe 1: Bilddateiformat für Farbpaletten
Nehmen Sie an, das Portable Anymap-Dateiformat solle um ein neues (fiktives!) Bildformat mit der “Magic Number” P9 ergänzt werden, mit dem sich Bilder mit Farbpaletten im ASCII-Textformat speichern lassen. Die Farbpalette eines Bildes darf dabei beliebig viele Farben enthalten, deren Anzahl und Farbwerte in der Datei an geeigneter Stelle mit gespeichert werden müssen.
Entwerfen Sie ein entsprechendes neues Dateiformat und beschreiben Sie den Aufbau der Datei. Veranschaulichen Sie das von Ihnen entworfene Dateiformat, indem Sie für das folgende Beispielbild angeben, wie die Datei konkret aussehen würde:
Das Dateiformat soll prinzipiell nach demselben Schema wie PNM aufgebaut sein. Der Header sollte auch hier mit der “Magic Number” (hier: P9) und der Bildgröße beginnen. Was danach kommt, ist Ihrer Fantasie überlassen.
-
Die Bezeichnung “Alpha” für die Transparenzinformation geht auf die Formel zur Anzeige des Bildes zurück, bei der jedes Bildpixel A mit seinem Transparenzfaktor α gewichtet mit dem entsprechenden Hintergrundpixel B verrechnet wird (“Alpha Blending”), um den angezeigten Pixelwert C zu berechnen: C = α⋅A + (1-α)⋅B. ↩︎
-
Diese Farbdarstellung wird als indizierte Farben bezeichnet. Ein Index ist die Nummer eines Eintrags in einer Tabelle (hier der Farbpalette). ↩︎
-
Später wurde PNM noch um ein weiteres Format namens Portable Arbitrary Map (PAM, “Magic Number” P7) erweitert, mit dem sich beliebige Bildformate mit 1–4 Kanälen und 8/16 Bit pro Kanal darstellen lassen. Dieses Format hat aber eine andere Struktur als die anderen PNM-Formate und wird nicht von allen Grafikprogrammen, die PNM-Dateien öffnen können, unterstützt. ↩︎
-
Die Bezeichnung “Portable Pixmap” wird zum Teil auch statt “Portable Anymap” als Stellvertreter für die Formatfamilie verwendet. ↩︎
-
Der Header kann nach der “Magic Number” außerdem Textkommentare enthalten, die immer durch das Zeichen
#eingeleitet werden und bis zum nächsten Zeilenumbruch laufen. Diese Kommentare werden beim Lesen einer PNM-Datei ignoriert, z. B.:
P2
# Erstellt am 24.08.2021
17 8
100 # max. Helligkeit
...↩︎
2.2.3 Grafische Codes
In vielen praktischen Anwendungen werden digitale Codes grafisch dargestellt, beispielsweise als Aufdruck auf Artikeln, Tickets oder Postern, so dass sie mit optischen Lesegeräten (z. B. Barcode-Scanner) oder Kameras eingelesen und automatisch interpretiert werden können.
Die in der Praxis am häufigsten verwendeten maschinenlesbaren grafischen Codes sind Barcodes (auch Strich-Code oder Balken-Code) und Matrix-Codes (auch 2D-Barcode oder Pixel-Code), die auch mit dem Smartphone mit Hilfe bestimmter Apps gescannt werden können.
Barcodes
Ein Barcode ist ein grafischer Code, der aus parallelen Balken und Lücken unterschiedlicher Breite besteht (in der Regel einfarbig und vertikal). Die digitalen Daten werden hier also als Binärfolgen (= Zeilenpixel) codiert, aus den sich die Darstellung der vertikalen Balken ergibt. Als Beispiel für einen Barcode, dem wir im Alltag sehr häufig begegnen, wird hier der EAN-Barcode behandelt, der für Artikelnummern verwendet wird.
EAN-Barcode
Der EAN-Barcode (EAN ist kurz für European Article Number) spezifiziert einen Barcode zur grafischen Codierung von global eindeutigen Artikelnummern (GTIN, kurz für Global Trade Item Number), der im Einzelhandel und anderen Branchen sehr verbreitet ist.1 Der Standard-EAN-Barcode hat 13 Ziffern (EAN-13), für kürzere Artikelnummern gibt es auch eine Variante mit 8 Ziffern (EAN-8). Oft ist die Artikelnummer zusätzlich als Klartext unterhalb des Barcodes abgebildet, so dass sie auch manuell erfasst werden kann, wenn das Einscannen nicht funktionieren sollte, beispielsweise weil der Barcode beschädigt ist.
Hier ein dekoratives Beispiel:2

GTIN/ISBN
Eine Artikelnummer im Format GTIN-13 ist immer nach dem folgenden Muster aufgebaut (ähnlich z. B. dem Erzeugercode auf Hühnereiern): Sie besteht aus 13 Ziffern, wobei üblicherweise die ersten 2–3 Ziffern das Länderpräfix3 darstellen, die folgenden 4–5 Ziffern den Hersteller des Produkts kennzeichnen und die folgenden 5 Stellen das Produkt selbst kennzeichnen. Die letzte Ziffer stellt eine Prüfziffer dar, die aus den restlichen 12 Stellen berechnet wird und anhand derer sich überprüfen lässt, ob die GTIN-13 eventuell falsch gelesen wurde (dazu unten mehr).
Eine ISBN (International Standard Book Number) bzw. ISBN-13 ist eine Sonderform der GTIN-13, die speziell zur Kennzeichnung von Büchern verwendet wird und ebenfalls mit dem EAN-Barcode dargestellt wird. Hier wird zu Beginn als Länderpräfix immer die Ziffernfolge 978 oder 979 verwendet (“Bookland”). Die Stellen 4–12 geben hier die Ländergruppe, Verlagsnummer und Titelnummer des Buches an.
Struktur
Der EAN-Barcode stellt die Ziffern der Artikelnummer durch vertikale schwarz-weiße Streifenmuster dar. Dabei werden nur die Stellen 2 bis 13 durch Streifenmuster dargestellt, die Ziffer an der ersten Stelle wird nur indirekt codiert (darauf kommen wir später zurück). Zur Codierung der Ziffern in Streifenmuster werden drei verschiedene Codetabellen verwenden, die hier “Code A”, “Code B” und “Code C” genannt werden.
Der Barcode ist folgendermaßen aufgebaut:
- Der Barcode besteht aus vertikalen Streifen gleicher Breite, die entweder schwarz oder weiß sind, und unterschiedlich breite “Balken” bilden.
- Insgesamt enthält der Barcode je 7 Streifen für jede der 12 dargestellten Ziffern, sowie je 3 abwechselnd schwarze und weiße Streifen als Randzeichen links und rechts und 5 als Trennzeichen in der Mitte.
- Links vom Trennzeichen werden die Stellen 2 bis 7 der Artikelnummer durch Streifenmuster dargestellt, rechts vom Trennzeichen die Stellen 8 bis 13.
- Die sechs Ziffern in der linken Hälfte werden mit den Streifenmustern aus den Tabellen “Code A” und “Code B” dargestellt.
- Die sechs Ziffern in der rechten Hälfte werden dagegen nur mit den Streifenmustern aus Tabelle “Code C” dargestellt (Invertierung von Code A).
Jede Ziffer wird also quasi durch einen 7-stelligen Binärcode codiert, so dass durch die schwarzen und weißen Streifen je zwei schwarze und zwei weiße Balken unterschiedlicher Breite pro Ziffer entstehen. Die Streifenmuster sind dabei so gewählt, dass erkannt werden kann, ob der Barcode von links oder von rechts gescannt wurde, so dass es dadurch nicht zu Verwechslungen kommen kann.
Codevarianten
Welche der beiden Codevarianten A oder B für eine Ziffer aus der linken Hälfte verwendet wird, hängt von der Position der Ziffer, sowie von der ersten Ziffer der Artikelnummer ab. Die Tabelle auf der rechten Seite stellt dar, in welcher Reihenfolge die beiden Codevarianten für die 6 Ziffern in der linken Hälfte in Abhängigkeit von der ersten Ziffer der Artikelnummer gewählt werden.
Die erste Ziffer ist im Barcode also indirekt über die Ziffern in der linken Hälfte codiert: Je nachdem, welchen Wert die 1. Ziffer hat, wird für jede der Ziffern an den Stellen 2–7 ein Streifenmuster aus Codetabelle A oder B gewählt. Beim Decodieren werden die Ziffern in der linken Hälfte mit den beiden Codetabelle A und B decodiert und aus der Reihenfolge der Codevarianten die 1. Ziffer decodiert.
Der Grund für diese umständliche Codierung der ersten Ziffer liegt darin, dass der EAN-Barcode den in den USA verbreiteten 12-stelligen UPC-Barcode (Universal Product Code) erweitert, so dass Lesegeräte für EAN-Barcodes auch UPC-Barcodes lesen können. Der UPC-Barcode verwendet dabei für die Ziffern in der linken Hälfte nur die Codevariante A, entspricht also einer GTIN-13 mit führender Null.
Interaktiver EAN-Barcode
Tool: Im folgenden interaktiven EAN-Barcode können Sie austesten, wie sich der Barcode für verschiedene Eingabewerte ändert. Klicken Sie auf eine Ziffer, um sie zu ändern oder tragen Sie eine GTIN über das Eingabefeld ein (ohne Bindestriche oder Leerzeichen). Mit den Schaltflächen können Sie die verwendeten Codierungen (A/B/C) anzeigen, Hilfslinien ein-/ausblenden und die Prüfziffer der Eingabe überprüfen.
Erkunden Sie den Aufbau des Barcodes beispielsweise folgendermaßen:
- Klicken Sie auf “Codierung anzeigen” und anschließend mehrmals auf die erste Ziffer, um zu sehen, wie sich die Codierungen in der linken Hälfte in Abhängigkeit von der ersten Ziffer ändern (Code A/B), während die Codierungen in der rechten Hälfte gleich bleiben (Code C).
- Klicken Sie auf “Prüfziffer anzeigen” und anschließend mehrmals auf Ziffern an geraden oder ungeraden Stellen, um zu sehen, wie sich die erwartete Prüfziffer ändert.
Im folgenden Abschnitt wird erläutert, wie die Prüfziffer zustandekommt.
Prüfziffer
Beim Einscannen des Barcodes kann es passieren, dass die GTIN-Artikelnummer falsch eingelesen wird, beispielsweise aufgrund von Verdeckungen, Deformationen oder Beschädigungen des Barcodes. Um solche Situationen zu erkennen, enthält die GTIN redundante Information: Konkret codieren nur die ersten 12 Ziffern die relevanten Informationen über das Produkt, während die letzte Ziffer (“Prüfziffer”) nach einer bestimmten Formel aus den übrigen Daten berechnet wird. So kann anhand der gelesenen Ziffern überprüft werden, ob bestimmte Fehler beim Einlesen aufgetreten sind.
Die Prüfziffer einer GTIN wird immer so gewählt, dass die Quersumme der 13 Ziffern, wobei alle Ziffern an geraden Stellen mit dreifacher Gewichtung in die Summe eingehen, ein ganzzahlig Vielfaches von 10 ergibt.
Die Prüfziffer der GTIN wird also mit dem folgenden Algorithmus berechnet:
- Summiere die ersten 12 Ziffern der GTIN. Multipliziere dabei alle Ziffern an geraden Stellen mit 3.
- Die Prüfziffer ist die Differenz der Summe zur nächstgrößeren Zahl, die ohne Rest durch 10 teilbar ist (oder 0 wenn die Summe selbst ohne Rest durch 10 teilbar ist).
Formel: Wenn also die einzelnen Ziffern der GTIN mit z1 bis z13 bezeichnet werden, ergibt sich die Prüfziffer z13 durch die folgende Formel:4
$$z_{13} = (10 - ((z_1 + 3 \cdot z_2 + z_3 + 3 \cdot z_4 + … + 3 \cdot z_{12}) \ mod \ 10)) \ mod \ 10$$
Beispiel: Für die ISBN 978-3-486-71751-? soll die Prüfziffer berechnet werden. Die Quersumme mit dreifacher Gewichtung der geraden Stellen ergibt:
$$9 + 8 + 4 + 6 + 1 + 5 + 3 \cdot (7 + 3 + 8 + 7 + 7 + 1) = 33 + 3 \cdot 33 = 132$$
Also lautet die Prüfziffer 8, nämlich die Differenz zu 140 bzw. das Ergebnis von:
$$z_{13} = (10 - (132 \ mod \ 10)) \ mod \ 10 = (10 - 2) \ mod \ 10 = 8$$
Die vollständige ISBN lautet also 978-3-486-71751-8.
Um eine gegebene GTIN zu überprüfen, wird einfach die gewichtete Quersumme inkl. Prüfziffer berechnet und geprüft, ob das Ergebnis ohne Rest durch 10 teilbar ist.
Beispiel: Der Barcode-Scanner liest aus einem EAN-Barcode die ISBN 978-1-234-56789-1. Die Quersumme mit dreifacher Gewichtung der geraden Stellen ergibt:
$$9 + 8 + 2 + 4 + 6 + 8 + 1 + 3 \cdot (7 + 1 + 3 + 5 + 7 + 9) = 38 + 3 \cdot 32 = 134$$
Das Ergebnis ist nicht ohne Rest durch 10 teilbar. Der EAN-Barcode ist also vom Barcode-Scanner falsch gelesen worden, er muss entweder erneut gescannt werden oder die Artikelnummer wird manuell eingegeben.
Matrix-Codes
Ein Matrix-Code stellt Binärdaten als zweidimensionale Muster dar, meist als schwarze und weiße quadratische Pixel innerhalb eines Rasters (einer Matrix). Im Gegensatz zu Barcodes können Matrix-Codes deutlich größere Datenmengen speichern und eignen sich so für verschiedenste Anwendungsfälle. Das erlaubt es auch, größere Mengen an redundanter Zusatzinformation zu speichern, so dass die Daten im Zweifelsfall auch dann noch korrekt ausgelesen werden können, wenn Teile des Codes verdeckt oder zerstört sind. Dadurch werden die Codierverfahren aber auch deutlich komplizierter als bei Barcodes.
Bekannte Beispiele sind der Actec-Code (z. B. auf Bahntickets), DataMatrix-Code (z. B. auf Briefmarken) und der QR-Code (vielseitig einsetzbar, u. a. zum Codieren von Internetadressen). Der folgende QR-Code codiert beispielsweise die URL dieses Online-Skripts – wird dieser QR-Code mit einer geeignete Smartphone-App gescannt, kann die URL im Browser geöffnet werden:
Fachkonzept: Prüfsumme
Bei den oben beschriebenen GTINs wurde eine zusätzliche Ziffer angehängt, so dass die (auf eine bestimmte Weise gewichtete) Quersumme ein Vielfaches von 10 ist. So konnte beim Lesen einer GTIN aus einem EAN-Barcode ggf. erkennt werden, ob die Daten falsch decodiert wurden. Hier wird also eine spezielle Prüfsumme zur Fehlererkennung verwendet.
Eine Prüfsumme (engl. checksum) ist allgemein ein Wert, der aus den Daten und zusätzlicher redundanter Information berechnet wird. Die redundante Information (hier die Prüfziffer) wird dabei so gewählt, dass die Prüfsumme eine bestimmte Eigenschaft hat. Das Lesegerät kann dann durch Berechnen der Prüfsumme und Überprüfen der erwarteten Eigenschaft die Daten validieren, also auf Fehler überprüfen, und bei Abweisungen eventuell sogar erkannte Fehler zu korrigieren.
Prüfsummenbasierte Verfahren stellen eine der einfacheren Möglichkeiten zur Fehlererkennung für digitale Daten dar, die eingelesen oder übertragen werden und dienen oft als Grundlage für komplexere Verfahren. Ziel ist es, typische Fehler zu erkennen, z. B. dass einzelne Werte oder Bits durch widrige Umstände vertauscht, ausgelassen, verdoppelt oder invertiert werden.
Als Prüfsumme für Sequenzen von Ziffern oder Ganzzahlen wird oft die Quersumme (= Summe über alle Elemente der Sequenz) oder die gewichtete Quersumme (mit fest vorgegebenen Gewichtungsfaktoren) verwendet und als Eigenschaft überprüft, ob diese ein ganzzahlig Vielfaches einer vorgegebenen Zahl M darstellt. Um diese Eigenschaft zu erreichen, werden ein oder mehrere Werte zur Sequenz hinzugefügt (Prüfziffern/-zahlen).
Beispiel: Bei der GTIN-13 wird eine zusätzliche Ziffer zur Sequenz aus 12 Ziffern hinzugefügt, so dass die mit den Faktoren 1, 3, 1, … gewichtete Quersumme ein ganzzahlig Vielfaches von 10 ergibt.
Parität
Für binäre Daten wird als Prüfsumme üblicherweise die Parität verwendet (= Quersumme modulo 2), die anschaulich angibt, ob die Anzahl der 1-Bits in einer Bitsequenz gerade (= 0) oder ungerade (= 1) ist. Hier wird an die Daten meist ein zusätzliches Bit angehängt (Paritätsbit), so dass die Parität der Bitsequenz inkl. Paritätsbit gerade ist.
Beispiel:
Die Bitsequenz 0110 0010 soll um ein Paritätsbit ergänzt werden, so dass die Gesamtparität gerade ist. Da die Bitsequenz 3 1-Bits enthält, muss das Paritätsbit auch den Wert 1 bekommen.
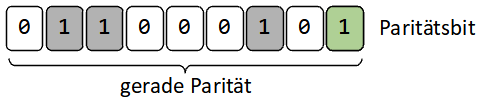
Ist die Parität einer gelesenen Bitsequenz ungerade, muss ein Fehler vorlegen. Mit einfacher Parität bleiben viele Fehler allerdings unentdeckt, beispielsweise wenn ein 0- und ein 1-Bit vertauscht werden oder wenn gleich viele 0- und 1-Bits “gekippt” sind (hier rot dargestellt):
Als Ausblick: Werden mehrere Paritätsbits für eine Bitsequenz verwendet, lässt sich die Fehlererkennung verbessern und Fehler ggf. sogar beheben.
-
Die entsprechenden Artikelnummern wurden früher ebenfalls als EAN bezeichnet, wurden aber 2005 in GTIN umbenannt. Trotzdem hat sich die Bezeichnung “EAN” für den Barcode zur grafischen Darstellung der Artikelnummern gehalten. ↩︎
-
Quelle: Shopblogger, https://www.shopblogger.de/blog/archives/23370-Lustige-Strichcodes-251.html ↩︎
-
Das Länderpräfix gibt Auskunft über das Land, das die GTIN für das Produkt vergeben hat, was nicht unbedingt auch das Produktionsland sein muss. Produkte, deren GTIN von Deutschland vergeben wurde, beginnen mit den Ziffernfolgen 40–43 oder 440. ↩︎
-
Die Operation x mod y (“Modulo”) berechnet den Teilungsrest der ganzzahligen Division von x durch y, zum Beispiel: 72 mod 7 = 2, da 72 / 7 = 10 Rest 2. ↩︎
2.2.4 Datenkompression
Einleitung
Im Alltag sind wir von immer größer werdenden Datenmengen umgeben, die wir auf Rechnern speichern oder durch das Internet schicken. Besonders kritisch sind Mediendaten wie Bilder, Tonaufnahmen und Videos – selbst Ihre Urlaubsfotosammlung würde als Rohdaten gespeichert schnell viele hundert Gigabyte einnehmen. Darüber hinaus müssen von relevanten Daten in regelmäßigen Abständen Sicherungskopien (Backups) erstellt und zum Teil über längere Zeit archiviert werden, was das Problem des Speicherbedarfs noch vergrößert. Aus diesem Grund sind Verfahren zur Datenkompression unerlässlich.
Verfahren zur Datenkompression sind dabei im Grunde nichts anderes als Codierungsverfahren – also Verfahren, die Daten von einer Repräsentation in eine andere umwandeln – mit zwei entscheidenden Eigenschaften:
- Die codierten Daten haben einen geringeren Speicherumfang als die Originaldaten (Kompression).
- Es gibt ein entsprechendes Decodierungsverfahren, mit dem die komprimierten Daten wieder in ihre ursprüngliche Repräsentation umgewandelt werden (Dekompression).
Dabei werden verlustfreie Kompressionsverfahren und verlustbehaftete Kompressionsverfahren unterschieden, je nachdem ob die Originaldaten bei Kompression und anschließender Dekompression exakt oder nur ungefähr wiederhergestellt werden (siehe Kompressionsverlust).
Anwendungen
Datenkompression wird in der Praxis unter anderem in “Packprogrammen” (auch Archivierungs- oder Kompressionsprogramme) verwendet, mit denen sich mehrere Dateien in einem komprimierten Format in eine Archiv-Datei verpacken lassen. Bekannte Dateiformate für solche komprimierten Archive sind etwa ZIP oder RAR (siehe auch Dateiformate). Solche Programme werden immer dann verwendet, wenn größere Datenmengen ein Problem darstellen – beispielsweise um Dateien per E-Mail zu verschicken, auf einer Webseite zum Download anzubieten oder auf einem Datenträger zu sichern.

Daneben wird Datenkompression auch häufig in Dateiformaten zur Codierung von Mediendaten – also Bild-, Audio- und Videodaten – verwendet, wobei hier oft auch verlustbehaftete Kompressionsverfahren zum Einsatz kommen, da hier Informationsverlust zugunsten stärker Speicherreduktion in einem gewissen Umfang tolerierbar ist. Fast alle heute gängigen Mediendateiformate wie JPEG oder PNG für Rastergrafiken, MP3 für Audiodaten oder MPEG für Videos verwenden Datenkompression, da umkomprimierte Mediendaten schnell sehr groß werden.
Kompressionsfaktor
Um zu beschreiben, wie stark Daten komprimiert werden, wird das quantitative Verhältnis zwischen komprimierten und unkomprimierten Daten verwendet.
- Der Kompressionsfaktor gibt an, wie groß die Daten nach der Kompression im Verhältnis zu den Originaldaten sind:
Kompressionsfaktor = komprimierte Datenmenge / originale Datenmenge
Dieser Faktor wird üblicherweise als Dezimalzahl, Prozentzahl oder Verhältnis in der Form “1 zu x” angegeben.
Wird beispielsweise eine Datei von ursprünglich 320 kB Größe auf 80 kB Größe komprimiert, beträgt der Kompressionsfaktor 80 / 320 = 0.25 (bzw. 25% oder 1 zu 4). - Die Kompressionsrate gibt umgekehrt das Verhältnis der originalen Dateimenge zur komprimierten Dateimenge an (im Beispiel also 4 zu 1).
Kompressionsverlust
Bei bestimmten Kompressionsverfahren gehen bei der Codierung und anschließenden Decodierung Teile der Information verloren, die Originaldaten können also nach der Kompression nicht mehr exakt wiederhergestellt werden. Solche verlustbehafteten Verfahren werden überwiegend zur Kompression von Bild-, Video- oder Audiodaten verwendet – dabei wird versucht, nur “unwichtige” Information zu reduzieren, also kleine Bilddetails oder leise Töne, deren Fehlen oder Verfremdung kaum auffällt. Hier lässt sich meistens durch einen Parameter steuern, wie stark die Daten komprimiert werden sollen, wobei mit zunehmender Kompressionsstärke die Bild- oder Tonqualität immer stärker leidet.
Beispiel: Das JPEG-Dateiformat für Rastergrafiken verwendet verlustbehaftete Kompression, deren Stärke sich über einen “Qualitätsfaktor” steuern lässt. Die folgende Übersicht zeigt ein Bild, das mit verschiedenen Qualitätsfaktoren komprimiert wurde, sowie die resultierenden Dateigrößen (in der Vergrößerung der rechten beiden Bilder lassen sich blockartige Bildstörungen erkennen, z. B. auf dem Leuchtturm):
 |
 |
 |
 |
 |
| Qualitätsfaktor 90% | Qualitätsfaktor 75% | Qualitätsfaktor 50% | Qualitätsfaktor 25% | Qualitätsfaktor 10% |
| Dateigröße 87 kB | Dateigröße 50.8 kB | Dateigröße 29.8 kB | Dateigröße 17.6 kB | Dateigröße 9.3 kB |
Bei der Kompression anderer Daten wie Textdateien oder Programmcode kommen solche Informationsverluste dagegen nicht in Frage: Hier müssen die Originaldaten aus den komprimierten Daten auf das Bit genau wieder hergestellt werden können. In dieser Lektion werden wir nur solche verlustfreien Kompressionverfahren betrachten.
Im Folgenden werden drei bekannte verlustfreie Kompressionsverfahren vorgestellt, die auch in der Praxis zur Datenkompression in verschiedenen Dateiformaten verwendet werden, und dabei unterschiedliche Grundstrategien verfolgen. Zur Veranschaulichung werden diese Verfahren hier auf kleine Beispiele zur Kompression von Textdaten und Bilddaten angewendet.
In den folgenden Beispielen werden die Ein- und Ausgabedaten der Einfachheit halber meistens als Textzeichen und Dezimalzahlen dargestellt. In der Praxis werden die Ausgabedaten der Kompressionsverfahren aber natürlich binär codiert.
Lauflängencodierung
Die Lauflängencodierung (engl. run-length encoding, kurz RLE) ist ein grundlegendes verlustfreies Kompressionsverfahren für beliebige Daten, das darauf abzielt, längere Wiederholungen von Zeichen zu komprimieren.
Die Idee ist relativ einfach: Statt Daten wie bisher Zeichen für Zeichen zu codieren, wird jeweils das Zeichen und seine “Lauflänge”, also wie oft es wiederholt wird, codiert. Die Ausgabe der Lauflängencodierung besteht dann abwechselnd aus Zeichen und Ganzzahlen.
Zur Kompression werden also die folgenden Schritte wiederholt, bis die Eingabe vollständig verarbeitet wurde:
- Lies solange ein Zeichen x aus der Eingabe, bis ein anderes Zeichen folgt, und zähle dabei, wie oft x nacheinander vorkommt (= Lauflänge N).
- Schreibe das Zeichen x und die Ganzzahl N in die Ausgabe.
Beispiel: Gegeben ist die Zeichenfolge:
A B B A C C C C D E A A A A A E E E E E E E E E
Nach Anwendung der Lauflängencodierung wird daraus (die Lauflängen sind hier blau markiert):
A 1 B 2 A 1 C 4 D 1 E 1 A 5 E 9
Hier reichen 4 Bit zur Codierung der Längenangaben aus. Wenn die 24 Textzeichen mit 8 Bit pro Zeichen codiert werden, erhalten wir einen Datenumfang von 24⋅8 Bit = 192 Bit, für die lauflängencodierten Daten dagegen nur 8⋅8 Bit (Zeichen) + 8⋅4 Bit (Längenangaben) = 96 Bit. Damit reduziert sich der Datenumfang auf 96 / 192 = 50%.
Bei der Dekompression werden also die folgenden Schritte wiederholt, wobei hier die komprimierten Daten als Eingabe abgearbeitet werden:
- Lies ein Zeichen x und eine Ganzzahl N aus der Eingabe.
- Schreibe das Zeichen x N-mal nacheinander in die Ausgabe.
Wie gut sich Daten durch die Lauflängencodierung komprimieren lassen, hängt davon ab, wie wahrscheinlich es ist, dass Zeichen wiederholt vorkommen. Im schlimmsten Fall kann sich der Datenumfang durch die Lauflängencodierung sogar vergrößern, wenn Zeichenwiederholungen selten sind und viele Zeichen einzeln stehen.
Beispiel: Gegeben ist die Zeichenfolge:
A B A C A D E E E E E B A C A
Nach Anwendung der Lauflängencodierung wird daraus:
A 1 B 1 A 1 C 1 A 1 D 1 E 5 B 1 A 1 C 1 A 1
Wenn 8 Bit pro Zeichen und 3 Bit pro Längenangabe verwendet werden, erhalten wir 15·8 Bit = 120 Bit für die unkomprimierten Daten, aber 11·8 Bit (Zeichen) + 11·3 Bit (Längenangaben) = 121 Bit für die lauflängencodierten Daten.
Verbesserte Lauflängencodierung
Aus diesem Grund werden bei der Lauflängencodierung Zeichen nur dann durch das Format Zeichen Lauflänge ersetzt, wenn sie geeignet oft wiederholt vorkommen, z. B. mindestens 3-mal in Folge. Anderenfalls bleiben die Zeichen unverändert.
Nun muss aber in der Ausgabe markiert werden, ob ein Zeichen mit oder ohne Längenangabe vorkommt. Anderenfalls kann bei der Decodierung nicht entschieden werden, ob es sich um ein einzelnes Zeichen oder eine Zeichenwiederholung handelt. Dazu wird üblicherweise ein bestimmtes Zeichen als “Markierungszeichen” ausgewählt. Dieses Zeichen markiert nun in der Ausgabe, dass eine Zeichenwiederholung im Format Zeichen Lauflänge folgt. Kommt in der Eingabe eine Zeichenwiederholung mit ausreichender Länge vor, wird diese also durch das Markierungszeichen, gefolgt vom Zeichen aus der Eingabe und der Länge der Wiederholung ersetzt.
Der Algorithmus zur Lauflängencodierung wird also folgendermaßen angepasst:
- Lies solange ein Zeichen x aus der Eingabe, bis ein anderes Zeichen folgt, und zähle dabei die Lauflänge N.
- Wenn N zu klein ist (z. B. N < 3): Schreibe x N-mal nacheinander in die Ausgabe.
- Anderenfalls: Schreibe Markierungszeichen, x und Lauflänge N in die Ausgabe.
Beispiel: Wir codieren eine Zeichenfolge, die sowohl einzelne Zeichen als auch Zeichenwiederholungen enthält:
A B A C A D E A A A A A E E E E E E E E E B A C C A B A A
Wenn das Zeichen “E” als Markierungszeichen für Zeichenwiederholungen verwendet wird, erhalten wir die folgende Ausgabe:
A B A C A D E E 1 E A 5 E E 9 B A C C A B A A
Die ersten 6 und letzten 8 Zeichen werden unverändert ausgegeben, da sie einzeln oder nur doppelt stehen. Die längeren Wiederholungen der Zeichen “A” und “E” werden im Lauflängenformat ausgegeben. Auch das einzelne Zeichen “E” muss im Lauflängenformat mit Länge 1 ausgegeben werden.
Bei 8 Bit pro Zeichen und 4 Bit pro Längenangabe erhalten wir hier: 14 einfache Zeichen (jeweils 8 Bit) + 3 Zeichenwiederholungen (jeweils 8 + 8 + 4 Bit = 20 Bit) = 172 Bit. Im Vergleich dazu: Bei Lauflängencodierung ohne Markierungszeichen werden je 8 + 4 Bit = 12 Bit für jedes einfache Zeichen und für jede Zeichenwiederholung benötigt, also 15·12 = 180 Bit. Je mehr weitere einzelne Zeichen in den Originaldaten enthalten wären, desto schlechter würde die Lauflängencodierung ohne Markierungszeichen im Vergleich zur verbesserten Version abschneiden.
Der Algorithmus zur Decodierung von lauflängencodierten Daten wird ebenfalls entsprechend angepasst:
- Lies ein Zeichen x aus der Eingabe.
- Wenn x das Markierungszeichen ist:
- Lies ein Zeichen y und eine Ganzzahl N aus der Eingabe.
- Schreibe das Zeichen y N-mal in die Ausgabe.
- Anderenfalls:
- Schreibe das Zeichen x in die Ausgabe.
Beachten Sie: Wenn in der Eingabe das Zeichen vorkommt, das die Rolle des Markierungszeichens übernimmt (hier: E), wird es immer in der Form “Markierungszeichen, Markierungszeichen, Lauflänge” ausgegeben, selbst wenn es einzeln steht. Daher sollte das Markierungszeichen so gewählt werden, dass es möglichst selten in den Eingabedaten vorkommt (bzw. selten einzeln steht). Wenn das Markierungszeichen beliebig gewählt werden kann, muss es zusammen mit den komprimierten Daten gespeichert werden (z. B. als erstes Zeichen zu Beginn), damit es bei der Decodierung bekannt ist.
Lauflängencodierung für Bilder
Die Lauflängencodierung kann natürlich nicht nur auf Textdaten angewendet werden, sondern prinzipiell auf beliebige Daten – beispielsweise auch auf Rasterbilddaten, wobei hier jeweils ein Grauwert oder ein RGB-Wert als einzelnes Zeichen betrachtet wird.
In Praxis zeigt sich, dass die Lauflängencodierung für die Kompression von Textdaten weniger gut geeignet ist, da mehrfache Zeichenwiederholungen in diesen eher selten vorkommen (abgesehen vielleicht von Steuerzeichen wie Leerzeichen oder Tabulatorzeichen bei mehrfach eingerückten Texten). Bei Rasterbilddaten kann sie dagegen sehr gute Ergebnisse erzielen, wenn die Bilder größere Bereiche mit gleicher Farbe und eher wenige Schattierungen/Farbverläufe enthalten.
Beispiel:
Zur Veranschaulichung soll die Lauflängencodierung hier auf ein 8-Bit-Grauwertbild der Größe 10 × 8 Pixel angewendet werden. Die Bilddaten bestehen hier aus 80 Grauwerten, die zeilenweise von oben links nach unten rechts aneinandergereiht werden. Als Markierungszeichen wird hier der Grauwert 0 (hex. 00) festgelegt, für die Codierung der Lauflängen werden 4 Bit verwendet (max. Längenangabe ist also 16).
In der Abbildung steht rechts neben den Bildzeilen, welche Grauwerte (hier im Hexadezimalformat) in der Zeile nacheinander wie oft vorkommen.
Wir erhalten hier das folgende (hier gekürzte) Ergebnis: Die obere Zeile stellt die Grauwerte und ihre Lauflängen in den Bilddaten dar, darunter steht die Ausgabe der Lauflängencodierung (die Längenangaben sind hier wieder als Dezimalzahlen dargestellt, in der “eigentlichen” Ausgabe werden sie als 4-Bit-Binärzahlen codiert).
Bitweise Lauflängencodierung
Wenn die Lauflängencodierung auf Bit-Ebene angewendet wird, also nur die beiden Werte 0 und 1 als Zeichen betrachtet werden, vereinfacht sich das Verfahren. Da Bitsequenzen abwechselnd aus Folgen von Nullen und Einsen bestehen, muss hier in der Ausgabe nicht explizit angegeben werden, welches Zeichen als nächstes folgt: Auf jede Null-Folge folgt eine Eins-Folge und umgekehrt. Daher reicht es bei der bitweisen Lauflängencodierung, die Längen der abwechselnd aufeinanderfolgenden Null- und Eins-Folgen auszugeben. Dabei muss vereinbart werden, ob sich die erste Längenangabe auf eine Null-Folge oder Eins-Folge bezieht (per Konvention üblicherweise auf eine Null-Folge).
Beispiel: Gegeben ist die folgende Bitsequenz (Leerzeichen hier nur zur besseren Übersicht):
1111 1110 0000 0111 1100 0001
Die Lauflängencodierung der Bitfolge ergibt nun die folgende Zahlenfolge:
0, 7, 6, 5, 5, 1
Die Längen der Null-Folgen sind hier der einfacheren Zuordnung halber grau dargestellt, die Längen der Eins-Folgen schwarz. Wenn hier jede Längenangabe als Ganzzahl mit 3 Bit gespeichert wird, erhalten wir als Resultat die folgende Bitsequenz (Leerzeichen hier nur zur besseren Übersicht):
000 111 110 101 101 001
Die Codelänge wurde damit von 24 Bit auf 18 Bit reduziert, also auf 75% der ursprünglichen Codelänge.
Dieses Verfahren lässt sich generell für Daten im Binärformat verwenden, unabhängig davon, was die Daten bedeuten – solange relativ häufig längere Bitfolgen mit demselben Wert erwartet werden. Besonders geeignet ist dieses Verfahren für die Kompression von Schwarz-Weiß-Bildern. Im folgenden Beispiel werden die Pixel eines 8×8-Schwarz-Weiß-Bildes zeilenweise von oben links nach unten rechts per Lauflängencodierung codiert:
Die Lauflängencodierung der Bitfolge ergibt die folgenden 17 Zahlen:
2, 4, 3, 6, 1, 1, 2, 2, 2, 18, 6, 1, 1, 6, 3, 4, 2
Wenn auch hier jede Längenangabe als Ganzzahl mit 3 Bit gespeichert wird, ist die maximal darstellbare Längenangabe 2³ − 1 = 7. Die Zahl 18 muss also durch die Zahlenfolge 7, 0, 7, 0, 4 ersetzt werden. Damit erhalten wir 21 Zahlen und eine Codelänge von 3 ⋅ 21 = 63 Bit. Ingesamt haben wir in diesem Beispiel also nur 1 Bit gespart.
Klarerweise wird die Kompressionsrate aber umso besser, je mehr aufeinanderfolgende schwarze bzw. weiße Pixel in den Eingabedaten vorkommen – beispielsweise bei einem Schwarz-Weiß-Scan einer Textseite, in dem sich große zusammenhängende weiße Bereiche mit kleineren schwarzen Bereichen abwechseln. Lauflängencodierung kommt daher unter anderem bei der Bildübertragung per Fax zum Einsatz.
Häufigkeitsbasierte Kompression
Bei der Lauflängencodierung werden direkt aufeinanderfolgende Zeichenwiederholungen ausgenutzt, um Daten zu komprimieren. Eine alternative Strategie besteht darin, Daten auf Grundlage der Häufigkeit der vorkommenden Zeichen zu komprimieren.1
Die Grundidee besteht darin, einzelne Zeichen nicht durch binäre Codewörter derselben Länge (z. B. 8 Bit pro Zeichen) zu codieren, sondern durch Codewörter unterschiedlicher Länge. Häufigere Zeichen werden dabei durch Codewörter kürzerer Länge repräsentiert und seltenere Zeichen durch längere Codewörter.
Der Morse-Code verwendet beispielsweise diese Strategie (die Buchstaben E und T werden mit nur einem Symbol codiert, J, Q, X und Z dagegen mit vier Symbolen). Beim Morsecode werden Pausen als Trennzeichen zwischen den Codewörtern verwendet, damit klar ist, wo ein Codewort endet und das nächste beginnt. Anderenfalls könnte eine Nachricht wie •••---••• nicht eindeutig als “SOS” decodiert werden, sondern könnte z. B. auch “EUGI” bedeuten.
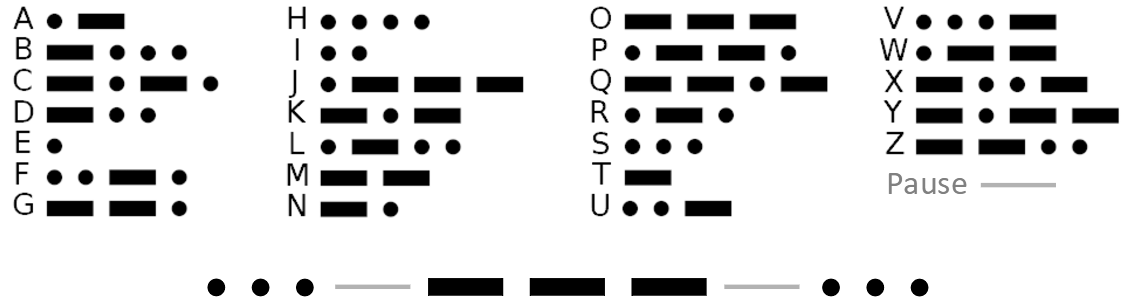
Wenn keine Trennzeichen zwischen Codewörten verwendet werden, muss sichergestellt sein, dass kein Codewort mit einem anderen Codewort beginnt. Eine solche Codierung heißt präfixfrei. Wenn beispielsweise ein Zeichen durch das binäre Codewort 01 repräsentiert wird, darf kein anderes Zeichen durch ein Codewort dargestellt werden, das mit der Bitfolge 01 beginnt, wie etwa 010 oder 0110. Anderenfalls ist die Decodierung nicht mehr eindeutig, wie das folgende Beispiel zeigt.
Beispiel: Angenommen, die zu codierenden Daten bestehen aus den Buchstaben A – F und wir ordnen diesen Zeichen die folgenden Codewörter zu:
A = 00, B = 01, C = 100, D = 11, E = 110, F = 111
Diese Codierung ist nicht präfixfrei, da die Codewörter für “E” und “F” jeweils mit dem Codewort für “D” beginnen.
Nun soll die Bitfolge 11100 decodiert werden. Hier ist nicht klar, ob das erste Zeichen ein “D” (Bitfolge 11) oder ein “F” (Bitfolge 111) ist, da es den codierten Daten nicht anzusehen ist, wie lang die einzelnen Codewörter sind. Die Bitfolge ließe sich gleichermaßen zu “DC” oder “FA” decodieren.
Die folgende Zuordnung von Codewörtern zu den Buchstaben ist dagegen präfixfrei:
A = 00, B = 01, C = 100, D = 101, E = 110, F = 111
Hier lässt sich die Bitfolge 11100 nur noch zu “FA” decodieren, die Decodierung ist also eindeutig.
Huffman-Codierung
Die Huffman-Codierung2 beschreibt ein Verfahren, um optimale binäre Codewörter basierend auf den Zeichenhäufigkeiten zu berechnen – also Codewörter, die zu einer möglichst kurzen Gesamtcodelänge führen. Das Verfahren garantiert dabei, dass die Codewörter präfixfrei, also eindeutig decodierbar sind.
Zur Codierung wird eine spezielle Datenstruktur, der sogenannte Huffman-Baum, aufgebaut, aus dem die Codewörter für die einzelnen Zeichen abgelesen werden können.
Codierung
Zuerst wird die Häufigkeit jedes Zeichens berechnet – es wird also gezählt, wie oft jedes Zeichen in den zu codierenden Daten vorkommt.
Anschließend wird der Huffman-Baum nach dem folgenden Algorithmus erstellt:
- Erstelle für jedes Zeichen einen einzelnen Knoten (also einen Baum mit nur einem Element), dessen Wert die Häufigkeit des Zeichens ist.
- Wiederhole, bis nur noch ein Baum übrig ist:
- Wähle die beiden Bäume, deren Wurzelknoten die geringsten Werte haben.
- Erstelle einen neuen Wurzelknoten, dessen Nachfolger die Wurzelknoten der beiden Bäume sind.
- Der Wert des neuen Wurzelknotens ist die Summe der Werte seiner beiden Nachfolger.
Beispiel: Die Textnachricht “OSTSEESPROTTENPOTT” soll mittels Huffman-Codierung komprimiert werden.
Als Erstes zählen wir, wie oft jedes Zeichen in der Nachricht vorkommt. Anschließend erstellen wir für jedes der sieben Zeichen einen Baum mit nur einem Knoten, dessen Wert die Häufigkeit des Zeichens ist.
Die Knoten für die Zeichen “N” und “R” haben die geringste Werte (jeweils 1), also werden sie mit einem neuen Wurzelknoten verbunden, dessen Wert 1 + 1 = 2 ist.
Nun haben der neue Baum und der Baum für das Zeichen “P” die geringsten Werte an der Wurzel stehen (jeweils 2). Ihre Wurzelknoten werden mit einem neuen Wurzelknoten dessen Wert 2 + 2 = 4 ist, zu einem neuen Baum verbunden.
Nun gibt es drei Knoten mit dem Wert 3. Es ist egal, welche der beiden wir in diesem Schritt verbinden. Hier werden die Knoten der Zeichen “O” und “S” gewählt und mit einem neuen Wurzelknoten mit dem Wert 3 + 3 = 6 verbunden.
Als Nächstes werden die Wurzelknoten der beiden Bäume mit den momentan geringsten Werten 3 und 4 verbunden. Der neue Baum hat den Wert 3 + 4 = 7 an der Wurzel stehen.
Nun werden die Wurzelknoten der beiden Bäume mit Werten 5 und 6 verbunden, der neue Wurzelknoten erhält den Wert 5 + 6 = 11.
Als Letztes werden die Wurzelknoten der letzten beiden Bäume mit Werten 7 und 11 verbunden, der neue Wurzelknoten erhält den Wert 7 + 11 = 18. Damit ist der Huffman-Baum fertiggestellt.
Auf diese Weise werden Schritt für Schritt jeweils zwei Bäume zusammengefügt, bis nur noch ein einziger Baum (der Huffman-Baum) übrig ist, dessen Wurzel als Wert die Gesamtanzahl aller Zeichen enthält. Jedes Blatt des Huffman-Baums repräsentiert ein Zeichen. Die Reihenfolge, in der die Bäume zusammengefügt werden, sorgt dafür, dass die Blätter seltenerer Zeichen weiter von den Wurzel entfernt sind, während die Blätter häufigerer Zeichen näher an der Wurzel liegen (gemessen in Kanten).
Aus dem Huffman-Baum lassen sich nun die Codewörter für jedes Zeichen ablesen. Dazu wird zuerst jede linke Kante von einem Knoten zu seinem Nachfolger mit 0 beschriftet und jede rechte Kante mit 1.
Um das Codewort für ein Zeichen zu ermitteln, wird dann folgendermaßen vorgegangen:
- Starte bei der Wurzel und gehe abwechselnd nach links oder rechts, bis das Blatt für das Zeichen erreicht ist.
- Die Bit-Werte auf den Kanten des Pfades von der Wurzel zum Blatt ergeben das Codewort für das Zeichen.
Beispiel:
Aus dem oben konstruierten Huffman-Baum erhalten wir das Codewort 01 für den Buchstaben “E”, da wir von der Wurzel aus erst nach links und anschließend nach rechts gehen müssen, um zum Blatt für das Zeichen “E” zu gelangen. Die Codewörter der einzelnen Buchstaben sind in der rechten Spalte der Tabelle eingetragen.
Damit erhalten wir die folgende Bitsequenz, wenn wir die gesamte Textnachricht Zeichen für Zeichen durch die Huffman-Codewörter ersetzen:
100101111010101101001000110011110100000011001111
Decodierung
Um eine Bitfolge zu decodieren, die mittels Huffman-Codierung entstanden ist, wird der Huffman-Baum benötigt, mit dem die Daten codiert wurden. Dabei dient die Bitfolge quasi als Anleitung, wie wir während der Decodierung durch den Huffman-Baum laufen. Immer wenn ein Blatt erreicht wird, wird das entsprechende Zeichen ausgegeben und bei der Wurzel neu gestartet.
Die Decodierung läuft also nach dem folgenden Algorithmus ab:
- Setze einen Zeiger auf den Wurzelknoten des Huffman-Baums.
- Wiederhole, bis die gesamte Bitfolge gelesen wurde:
- Lies das nächste Bit.
- Wenn das Bit
0ist, setze den Zeiger auf den linken Nachfolger des aktuellen Knotens, bei1auf den rechten. - Wenn ein Blatt erreicht wurde, gib das Zeichens des Blatts aus und setze den Zeiger auf den Wurzelknoten zurück.
Beispiel:
Mit dem oben konstruierten Huffman-Baum werden die ersten drei Bit 100 des Huffman-Codes zum Zeichen “O” decodiert: Beim Lesen der Bits wird von der Wurzel aus einmal nach rechts und anschließend zweimal nach links gegangen. Dabei wird das Blatt des Zeichens “O” erreicht, dieses Zeichen ausgegeben und der Zeiger auf den Wurzelknoten zurückgesetzt.
Speicheraufwand
In dem oben gezeigten Beispiel ergibt sich eine Codelänge von 48 Bit. Zum Vergleich: Wenn die Textdaten unkomprimiert im üblichen (erweiterten) ASCII-Format gespeichert werden, werden 8 Bit pro Zeichen benötigt – da die Nachricht 18 Zeichen enthält also ingesamt 8·18 = 144 Bit. Damit beträgt der Kompressionsfaktor der Huffman-Codierung hier 48 / 144 = 33.3%, die Kompressionsrate liegt bei 3 : 1.
Wenn wir stattdessen jedes Zeichen mit einem Codewort der gleichen Länge codieren würden, würden wir 3 Bit pro Zeichen benötigen, um die 7 verschiedenen Buchstaben im Text zu unterscheiden – insgesamt also 3·18 = 54 Bit. Der Kompressionsfaktor für dieses Verfahren beträgt hier 54 / 144 = 37.5%, schneidet also schlechter ab als die Huffman-Codierung.
Bei dieser Berechnung wird allerdings ignoriert, dass zusätzlicher Speicherbedarf für den Huffman-Baum nötig ist: Da der Huffman-Baum zur Decodierung bekannt sein muss, muss er zusammen mit den komprimierten Daten gespeichert werden. Wenn die Eingabedaten groß genug sind, wiegt die Speicherersparnis, die sich durch das Komprimieren der Daten ergibt, den zusätzlichen Speicherbedarf für den Huffman-Baum aber wieder auf.
Wörterbuchbasierte Kompression
Bestimmte Zeichenfolgen kommen in der Regel mit unterschiedlicher Häufigkeit in Daten vor. So enthalten deutschsprachige Texte beispielsweise sehr häufig Zeichenfolgen wie “ein”, “der”, “die” oder “sch”. Solche häufig vorkommenden Zeichenfolgen können ebenfalls ausgenutzt werden, um Daten zu komprimieren. Dazu werden Tabellen verwendet, die Zeichenfolgen auf binäre Codewörter abbilden und als Wörterbücher bezeichnet werden.
Bei wörterbuchbasierten Kompressionsverfahren besteht also die Grundidee darin, dass nicht nur einzelne Zeichen codiert werden, sondern auch häufiger vorkommende Zeichenfolgen durch einzelne Codewörter dargestellt werden. Dazu muss zunächst ermittelt werden, welche Zeichenfolgen besonders oft in den zu codierenden Daten vorkommen. In einem Wörterbuch wird für jedes Zeichen und jede Zeichenfolge ein Codewort festgehalten, durch den diese in der Ausgabe dargestellt werden. Das Codewort ist dabei in Regel einfach die Nummer des Eintrags im Wörterbuch (binär codiert).
Um die Daten zu decodieren, muss das Wörterbuch bekannt sein. Wenn es möglich ist, das Wörterbuch während der Decodierung mit derselben Strategie zu rekonstruieren, mit der es während der Codierung aufgebaut wurde, kann aber darauf verzichtet werden, das Wörterbuch mit den komprimierten Daten zusammen zu speichern.
LZW-Algorithmus
Ein sehr bekanntes Kompressionsverfahren, das auf dieser Idee basiert, ist der Lempel-Ziv-Welch-Algorithmus (kurz LZW-Algorithmus).3
Beim LZW-Algorithmus wird während der Codierung der Eingabedaten ein Wörterbuch aufgebaut, in das Schritt für Schritt Zeichenfolgen steigender Länge, die bisher aus den Eingabedaten gelesen wurden, hinzugefügt werden. Das Codewort für eine Zeichenfolge im Wörterbuch ist dabei die Nummer des Eintrags, also die Position des Eintrags im Wörterbuch (binär codiert als Bitfolge) – der LZW-Algorithmus liefert als Ausgabe also eine Sequenz von Nummern von Wörterbucheinträgen. Der Einfachheit halber werden diese Nummern im Folgenden immer als Dezimalzahlen dargestellt.
Codierung
Zu Beginn enthält das Wörterbuch je einen Eintrag für alle Zeichen, die in der zu codierenden Nachricht vorkommen. Die Einträge des Wörterbuchs werden beginnend mit 0 durchnummeriert.
Der Algorithmus zur Codierung ist folgendermaßen beschrieben:
- Starte am Anfang der Eingabe.
- Wiederhole, bis die Eingabe vollständig verarbeitet wurde:
- Lies zeichenweise eine Zeichenfolge s aus der Eingabe, bis die Zeichenfolge s + das folgende Zeichen nicht mehr im Wörterbuch vorkommt.
- Schreibe die Eintragsnummer von s in die Ausgabe.
- Füge als neuen Wörterbucheintrag s + das folgende Zeichen hinzu.
- Verarbeite die Eingabe nun ab dem folgenden Zeichen weiter.
Beispiel: Der schrittweise Ablauf des Algorithmus soll anhand der Codierung der Textnachricht “ANANASBANANA” veranschaulicht und erläutert werden:
Das initiale Wörterbuch enthält vier Einträge für die Buchstaben “A”, “B”, “N” und “S” mit den Nummern 0 bis 3.
Das Zeichen “A” wird gelesen (längere Zeichenfolgen enthält das Wörterbuch zu diesem Zeitpunkt noch nicht).
Die Eintragsnummer des Zeichens “A” wird in die Ausgabe geschrieben, also 0.
Als neuer Eintrag mit der Nummer 4 wird die Zeichenfolge “AN” zum Wörterbuch hinzugefügt.
Das Zeichen “N” wird gelesen (das Wörterbuch enthält die nächstlängere Zeichenfolge “NA” bisher nicht).
Die Eintragsnummer des Zeichens “N” wird in die Ausgabe geschrieben, also 2.
Als neuer Eintrag Nummer 5 wird “NA” hinzugefügt.
Die Zeichenfolge “AN” wird gelesen, die im 1. Schritt zum Wörterbuch hinzugefügt wurde.
Die Eintragsnummer 4 der Zeichenfolge “AN” wird ausgegeben.
Als neuer Eintrag Nummer 6 wird “ANA” hinzugefügt.
Das Zeichen “A” wird gelesen (das Wörterbuch enthält die nächstlängere Zeichenfolge “AS” bisher nicht).
Die Eintragsnummer 0 des Zeichens “A” wird in die Ausgabe geschrieben.
Als neuer Eintrag Nummer 7 wird “AS” hinzugefügt.
Nach diesem Schema wird fortgefahren, solange noch Zeichen aus der Eingabe abzuarbeiten sind.
Nach diesem Schema wird fortgefahren, solange noch Zeichen aus der Eingabe abzuarbeiten sind.
Nach diesem Schema wird fortgefahren, solange noch Zeichen aus der Eingabe abzuarbeiten sind.
Im letzten Schritt wird kein neuer Eintrag zum Wörterbuch hinzugefügt.
Als Ausgabe erhalten wir hier die folgende Sequenz von Eintragsnummern:
0, 2, 4, 0, 3, 1, 6, 5
Verwenden Sie den folgenden Simulator, um diesen Algorithmus selbst Schritt für Schritt bis zum Ende nachzuvollziehen.
Interaktiver LZW-Codierer
Tool:
In dieser interaktiven Anzeige können Sie die LZW-Codierung einer Textnachricht Schritt für Schritt simulieren und dabei den Aufbau des Wörterbuchs nachvollziehen. Die letzte Spalte “Codewort” stellt hier die Nummer des Wörterbucheintrags als Binärzahl dar, die für die Ausgabe im Binärformat verwendet wird.
Mit der Schaltfläche “Nächster Schritt” wird die nächste Zeichenfolge aus der Eingabe gelesen und codiert. Wählen Sie “Codierung zurücksetzen”, um eine neue Textnachricht einzugeben.
ANANASBANANA
| Nummer | Zeichenfolge | Codewort |
|---|
Decodierung
Für die Decodierung muss nicht das vollständige Wörterbuch bekannt sein, es wird nur der Initialzustand benötigt, also die Einträge für die einzelnen Zeichen, die in der codierten Nachricht vorkommen. Alle weiteren Einträge werden während der Decodierung Schritt für Schritt rekonstruiert.
Die Decodierung startet also mit demselben initialen Wörterbuch wie die Codierung. Als Eingabe dient hier die Sequenz der Eintragsnummern, die bei der Codierung erzeugt wurde.
- Wiederhole, bis die Eingabe vollständig verarbeitet wurde:
- Lies die nächste Nummer N aus der Eingabe.
- Schreibe die Zeichenfolge, die im N-ten Wörterbucheintrag steht, in die Ausgabe.
- Füge als neuen Wörterbucheintrag die folgende Zeichenfolge hinzu: die im letzten Schritt ausgegebene Zeichenfolge + das erste Zeichen der im aktuellen Schritt ausgegebenen Zeichenfolge (im 1. Schritt der Decodierung wird diese Anweisung übersprungen)
Die letzte Anweisung wirkt auf den ersten Blick etwas seltsam: Hier wird das Hinzufügen der neuen Wörterbucheinträge während der Codierung nachvollzogen, allerdings mit einem Schritt Verzögerung.4
Hierdurch ergibt sich ein Fallstrick: Bei der Codierung kann es passieren, dass eine Zeichenfolge zum Wörterbuch hinzugefügt wird und gleich im nächsten Schritt für die Ausgabe verwendet wird. Überprüfen Sie als Beispiel die Codierung des Textes “ABABABA” im interaktiven LZW-Codierer:
- Im 3. Schritt wird die Nummer des Eintrags “AB” ausgegeben und als neuer Eintrag Nummer 4 die Zeichenfolge “ABA” hinzugefügt.
- Im 4. Schritt wird die Nummer des Eintrags “ABA” ausgegeben, der im vorigen Schritt zum Wörterbuch hinzugefügt wurde.
Bei der Decodierung tritt nun 4. Schritt also das Problem auf, dass die Nummer 4 decodiert werden soll, der 4. Eintrag aber erst in diesem Decodierungsschritt zum Wörterbuch hinzugefügt wird. Wie lautet also die Zeichenfolge mit der Nummer 4?
Dieses Problem lässt sich durch die folgenden Überlegungen lösen:
- Laut Decodierungsalgorithmus wird in diesem Schritt als neuer Wörterbucheintrag (Nummer 4) die im letzten Schritt ausgegebene Zeichenfolge + das erste Zeichen der im aktuellen Schritt auszugebenden Zeichenfolge eingetragen.
- Im letzten Schritt wurde “AB” ausgegeben, also lautet der neue Wörterbucheintrag “AB?”, wobei das Zeichen ? noch unbekannt ist.
- In diesem Schritt wird also “AB?” ausgegeben, die im aktuellen Schritt ausgegebene Zeichenfolge beginnt also mit “A”.
- Also ist “A” das unbekannte Zeichen ?, die Zeichenfolge, die in diesem Schritt ausgegeben und zum Wörterbuch hinzugefügt wird, lautet demnach “ABA”.
Generell wird in dieser Situation also immer die im letzten Schritt ausgegebene Zeichenfolge + deren erstes Zeichen zum Wörterbuch hinzugefügt und ausgegeben.
Binäre Codewörter
Im einfachsten Fall werden die Nummern, die der LZW-Algorithmus als Ausgabe produziert, als binär codierte Ganzzahlen mit fester Bitlänge (z. B. 12 Bit pro Nummer) repräsentiert. Das Wörterbuch kann dann aber nur eine begrenzte Anzahl von Einträgen aufnehmen (bei 12 Bit/Nummer insgesamt 212= 4096 Einträge). Wenn das Wörterbuch während der Codierung/Decodierung seine maximale Größe erreicht, können keine weiteren Einträge mehr hinzugefügt werden und im weiteren Verlauf nur die bereits vorhandenen Einträge verwendet werden.
Dieses Verfahren ist außerdem unnötig speicheraufwendig: Angenommen, das Wörterbuch enthält zu Beginn 10 Einträge. Dann reichen 4 Bit, um die Nummern der Einträge zu Beginn der Codierung darzustellen. Erst wenn das Wörterbuch nach 6 Schritte 16 Einträge umfasst, sind ab dann 5 Bit nötig, um die Nummern in der Ausgabe darzustellen. Verdoppelt sich die Anzahl der Einträge nach weiteren 16 Schritten auf 32, ist ein weiteres Bit nötig.
Diese Strategie wird beim LZW-Algorithmus verwendet: Es werden immer nur soviele Bit zur Codierung der Nummern in der Ausgabe verwendet, wie nötig sind, um die Nummern aller momentan im Wörterbuch vorhandenen Einträge darzustellen. Sobald die Wörterbuchlänge die nächste Zweierpotenz erreicht, wird 1 Bit zur Binärdarstellung der Nummern in der Ausgabe dazugenommen.
Bei der Decodierung wird die gleiche Strategie verwendet, um zu bestimmen, wie viele Bit jeweils für das nächste Codewort aus der Eingabe gelesen werden. Kurz zusammengefasst gilt in jedem Schritt: Wenn das Wörterbuch N Einträge enthält, werden ⌈log2(N)⌉ Bit für jedes Codewort gelesen/ausgegeben.
Im interaktiven LZW-Codierer können Sie über die Option ☑ binäre Ausgabe? nachvollziehen, wie die Codewörter im Binärformat mit wachsender Länge ausgegeben werden (die Leerzeichen dienen hier nur dazu, dass Sie die einzelnen Codewörter in der Ausgabe einfacher auseinanderhalten können).
Dateiformate
Die Kompressionsverfahren, die in dieser Lektion exemplarisch vorgestellt werden, finden (zum Teil in modifizierter Form) in vielen gängigen Dateiformaten Verwendung. Da die Verfahren unterschiedliche Stärken haben, werden sie meistens nicht einzeln, sondern in Kombination angewendet. Sehr verbreitet ist beispielsweise der “Deflate”-Algorithmus: Dabei wird neben der Huffman-Codierung eine spezielle Variante des Lempel-Ziv-Algorithmus verwendet, der dem LZW-Algorithmus ähnlich ist.
Abschließend finden Sie hier einen kurzen Überblick über bekannte Dateiformate für Rastergrafiken und Archive und die darin verwendeten Kompressionsverfahren.
| Dateiformate für Rastergrafiken | |
|---|---|
| Das JPEG-Format verwendet verlustbehaftete Kompression, wobei sich über einen Parameter das Verhältnis zwischen Kompressionsfaktor und Bildqualität steuern lässt. Je höher der Kompressionsfaktor, desto ungenauer lässt sich das Originalbild rekonstruieren. Der JPEG-Algorithmus verwendet dabei Lauflängencodierung und Huffman-Codierung als Zwischenschritte. | |
| Das PNG-Format verwendet unter anderem eine Kombination von Lempel-Ziv-Algorithmus und Huffman-Codierung (“Deflate”-Algorithmus). Die Codierung ist also verlustfrei. | |
| Das GIF-Format verwendet dagegen nur den LZW-Algorithmus und erreicht dadurch eine geringere Kompression als PNG. | |
| Windows Bitmap (BMP) verwendet nur Lauflängencodierung und erreicht dadurch nur eine schwache Kompression. | |
| Das TIFF-Format unterstützt verschiedene Kompressionsverfahren, unter anderem LZW und Lauflängencodierung, aber auch verlustbehaftete Kompression. |
| Dateiformate für Archive | |
|---|---|
| Das ZIP-Dateiformat (von engl. zipper = Reißverschluss) ist ein Format für verlustfrei komprimierte Dateien, das zur Archivierung oder zum Versand von Dateien verwendet wird. Die Dateien werden dabei einzeln komprimiert und in einer Archiv-Datei zusammengefasst. ZIP unterstützt verschiedene verlustfreie Kompressionsverfahren. Standardmäßig wird der “Deflate”-Algorithmus verwendet (Kombination von Lempel-Ziv-Algorithmus und Huffman-Codierung). | |
| Das RAR-Dateiformat5 ist ein Archiv-Dateiformat, das stärkere Kompression als ZIP erreicht. Das Dateiformat ist allerdings nicht frei und der Kompressionsalgorithmus nicht offen zugänglich, weswegen RAR inzwischen weniger stark verbreitet ist. |
-
Kompressionsverfahren, die den einzelnen Zeichen der zu codierenden Daten basierend auf ihrer Häufigkeit unterschiedlich lange Bitfolgen zuordnen, werden unter der Bezeichnung Entropiecodierung zusammengefasst. Die Entropie ist in der Informationstheorie anschaulich ausgedrückt ein Maß dafür, wie gleichmäßig die Zeichen in den zugrundeliegenden Daten verteilt sind. ↩︎
-
Die Huffman-Codierung ist nach ihrem Entwickler David A. Huffman benannt, der das Verfahren 1952 publizierte. ↩︎
-
Der LZW-Algorithmus ist nach seinen ursprünglichen Entwicklern Abraham Lempel und Jacob Ziv, sowie nach Terry A. Welch benannt. Lempel und Ziv veröffentlichten 1977 die erste Version des Verfahrens unter dem Namen LZ77, sowie 1978 dessen Nachfolger LZ78, der nach Detailverbesserungen durch Welch 1984 unter dem Namen LZW publiziert wurde. ↩︎
-
Zur Erklärung: Bei der Codierung wird in jedem Schritt die aktuell verarbeitete Zeichenfolge + das erste Zeichen der im nächsten Schritt verarbeiteten Zeichenfolge zum Wörterbuch hinzugefügt. Bei der Decodierung wird analog dazu in jedem Schritt die im vorigen Schritt ausgegebene Zeichenfolge + das erste Zeichen der aktuell ausgegebenen Zeichenfolge zum Wörterbuch hinzugefügt. ↩︎
-
Das RAR-Dateiformat (“Roshal ARchive”) ist nach seinem Entwickler Jewgeni Lasarewitsch Roschal benannt. ↩︎
2.3 Informationsdarstellung im Internet
World Wide Web
Wenn Sie mit ihrem Rechner oder Smartphone durch das Internet surfen um beispielsweise Informationen zu recherchieren, Bilder und Videos abzurufen oder online einzukaufen, nutzen Sie in den Regel einen konkreten Dienst des Internets, nämlich das World Wide Web.
Das World Wide Web (kurz “WWW” genannt) ist ein Informationssystem, das aus untereinander verknüpften Dokumenten – den Webseiten – besteht, die über das Internet bereitgestellt werden und weltweit auf vielen Rechnern verteilt gespeichert sind. Diese Webseiten stellen Informationen in Form von strukturierten Texten, Bildern, Videos und anderen Multimedia-Elementen dar. Sie enthalten Verweise (Hyperlinks) zu weiteren Webseiten und Dokumenten, über die diese abgerufen werden können. Auf diese Weise kann zwischen Webseiten hin- und hergewechselt werden kann. Ein solches System von vernetzten Text- und Mediendokumenten wird als Hypertext- oder Hypermedia-System bezeichnet.
Eine Website ist dabei ein Internetauftritt, der in der Regel aus mehreren, untereinander verknüpften Webseiten (engl. web pages) besteht. Websites werden umgangssprachlich auch “pars pro toto” nach ihrer Einstiegsseite als Homepage bezeichnet.
Webseiten
Um Webseiten anzuzeigen wird ein Webbrowser benötigt (z. B. Firefox, Chrome oder Edge) – also ein bestimmtes Anwendungsprogramm auf Ihrem Rechner, das Webseiten-Dokumente aus dem Internet anfordert und darstellt. Dieses Programm fungiert also als Web-Client.1
Um eine Webseite aufzurufen, geben Sie in Ihrem Browser deren Webadresse (URL, kurz für Uniform Resource Locator) ein.2 Ihr Browser schickt anschließend über das Internet eine Anfrage an den Webserver – also das Programm, das die Daten der Website bereitstellt und über die gegebene URL erreichbar ist. Der Webserver antwortet, indem er das angeforderte Webseiten-Dokument an Ihren Browser zurückschickt. Das Webseiten-Dokument wird dabei als Textdatei in einem bestimmten Format dargestellt, nämlich als HTML-Datei. Ihr Browser nimmt dieses Dokument entgegen, interpretiert es und präsentiert es grafisch aufbereitet so, dass Sie mit der Webseite interagieren können.
Zur Darstellung der Webseite liefert der Webserver ggf. noch weitere benötigte Dateien zurück, zum Beispiel Bilder, die in der Seite dargestellt werden. Informationen über die grafische Gestaltung der Webseiten werden in der Regel ebenfalls in separaten Dateien neben den HTML-Dateien bereitgestellt, die ein anderes Format verwenden, nämlich in Form von CSS-Dateien.
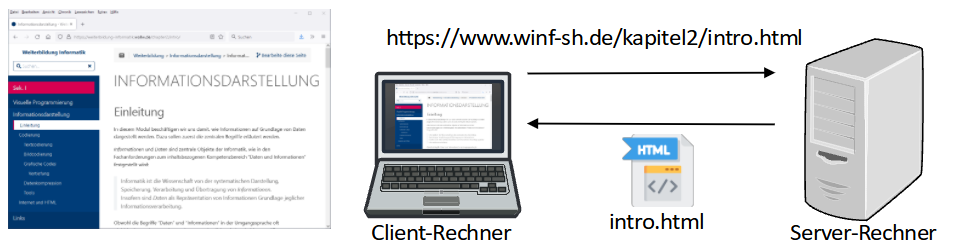
Beschreibung von Webseiten
In den folgenden Lektionen werden wir einen näheren Blick darauf werfen, wie Informationen im Internet dargestellt werden – also HTML zur Beschreibung der Struktur von Webseiten und CSS zur Beschreibung der grafischen Gestaltung – und wie sich Webseiten mit HTML/CSS selbst erstellen und gestalten lassen.
Wie die Kommunikation zwischen Webserver und -client über das Internet konkret umgesetzt ist und die Webdokumente auf Ihren Rechner kommen, werden wir an dieser Stelle nicht weiter beleuchten – dieses Thema wird ausführlich im später folgenden Kapitel “Netzwerke und Internet” behandelt.
-
Als Client wird ein Computerprogramm bezeichnet, das auf dem Endgerät eines Netzwerks ausgeführt wird und mit einem Server kommuniziert, also einem Computerprogramm, das meist auf einem anderen Gerät im Netzwerk ausgeführt wird und Daten bereitstellt, die von den Clients abgerufen werden. ↩︎
-
Die URL können Sie sich hier noch der Einfachheit halber ähnlich wie eine Dateiangabe mit Dateipfad vorstellen, nur dass in diesem Fall eine Datei auf einem anderen Rechner im Internet adressiert wird. Die URL
https://www.winf-sh.de/kapitel2/intro.htmlbezieht sich beispielsweise auf eine Dateiintro.html, die in einem Unterverzeichniskapitel2auf dem Rechner liegt, der im Internet über die Adressewww.winf-sh.deerreichbar ist. ↩︎
2.3.1 Strukturierung mit HTML
Wie ist eine Webseite aufgebaut? Welche Arten von Elementen kann sie enthalten? Und wie lässt sich die Struktur von Webseiten beschreiben, so dass ein Browser sie interpretieren und uns präsentieren kann? Dazu wird eine speziell dafür entwickelte Sprache verwendet, nämlich HTML.
In dieser Lektion werden wir uns mit den grundlegenden Konzepten und Bestandteilen von HTML beschäftigen, die nötig sind, um einfache Webseiten mit einem Texteditor selbst zu erstellen und ihren Aufbau nachzuvollziehen. Ziel ist es nicht, einen vollständigen Überblick über HTML zu bekommen, sondern einen Einstiegspunkt zu finden und die grundlegende Idee zur Beschreibung strukturierter Hypertext-Dokumente anhand von HTML nachzuvollziehen. Zur Vertiefung eignen sich HTML-Referenzen und Tutorials wie W3Schools oder SELFHTML.
HTML
HTML steht kurz für Hypertext Markup Language (also “Auszeichnungssprache für Hypertext”) und stellt eine formale Sprache dar, mit der sich die Struktur von Webseiten in textueller Form beschreiben lässt. Dabei ist in erster Linie die semantische Struktur (Gliederung nach Bedeutung) gemeint, nicht die visuelle Struktur (grafische Präsentation) der Webseiten.
Im Rahmen der Weiterbildung wird ausschließlich die aktuelle HTML-Version HTML5 betrachtet, die langfristig ältere HTML-Standards als Kernsprache des World Wide Web ablöst. “HTML” wird im Folgenden also gleichbedeutend mit “HTML5” verwendet, wenn nicht anderes angegeben.
Webseiten werden in ihrer einfachsten Form wie Textdokumente gegliedert und formatiert, also mit Hilfe von Strukturelementen wie Überschriften, Absätzen, Listen und Tabellen. Weitere wichtige Elemente von Webseiten sind Hyperlinks (kurz “Links”), also speziell markierte Textteile, die Verweise zu anderen Webseiten darstellen, sowie eingebettete Bilder oder andere Multimedia-Elemente.
Eine HTML-Datei ist eine reine Textdatei, in der die Inhalte und die Struktur einer Webseite mit HTML beschrieben werden. Dazu werden Textabschnitte auf eine bestimmte Weise mit zusätzlicher Bedeutung versehen – sie werden also semantisch markiert oder “ausgezeichnet” (engl. to markup)1 – so dass ein Webbrowser sie interpretieren und geeignet darstellen kann.
Einstiegsbeispiel
Als anschauliches Beispiel wird hier eine sehr einfach aufgebaute Website betrachtet,2 die Sie unter der folgenden URL im Browser öffnen können:
https://sekii.informatik-sh.de/content/examples/bandpage/index.html
Die Website besteht aus mehreren Webseiten und Bildern, die wie folgt miteinander verknüpft sind (die Datei index.html dient hier als Einstiegsseite):
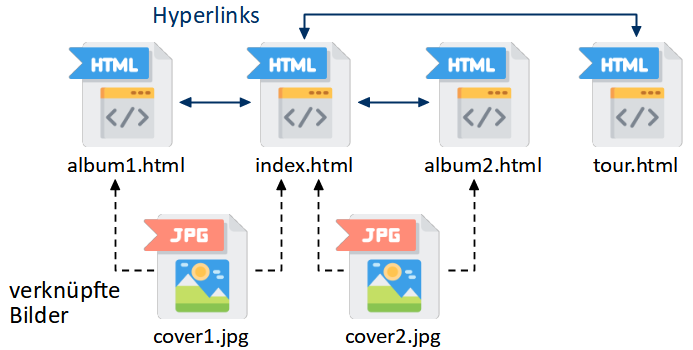
Sie können den HTML-Quelltext einer Webseite selbst im Browser untersuchen, indem Sie die Webseite öffnen, anschließend einen Rechtsklick auf die Seite ausführen und im Kontextmenü “Quelltext anzeigen” auswählen (je nach verwendetem Webbrowser heißt der Menüeintrag leicht unterschiedlich).
Die folgende Abbildung zeigt rechts den HTML-Quelltext der Webseite und links zum Vergleich die Präsentation der Webseite im Browser (zum Vergrößern anklicken):


Im Quelltext lassen sich ab Zeile 10 alle Textinhalte der Seite wiederfinden. Dabei lässt sich erkennen, dass Textabschnitte durch bestimmte Zeichenfolgen markiert sind, die ihnen eine spezielle Bedeutung verleihen – beispielsweise in Zeile 10:
<h1>Bandpage der Crispy Crablets</h1>
Hier stehen zu Beginn und am Ende der Zeile die Zeichenfolgen <h1> und </h1>, durch die der Beginn und das Ende einer Überschrift markiert wird (“h1” steht für dabei für heading level 1). Solche Zeichenfolgen in spitzen Klammern werden als Auszeichnungen oder Tags bezeichnet (engl. tag = Markierung, Etikett). Tags treten meistens paarweise in Form eines “öffnenden” und eines “schließenden” Tags auf und umschließen einen Inhalt, der durch die Tags semantisch beschrieben wird.
Tags
Tags sind also bestimmte Zeichenfolgen in HTML, mit denen sich Textteile und Abschnitte mit bestimmten Bedeutungen versehen lassen, die durch den Browser interpretiert werden. Mittels Tags lassen sich unter anderem die Inhalte der Seite gliedern. Im Beispiel sind mehrere solcher Tags zu finden:
Überschriften:
Die Hauptgliederung ist durch Überschriften verschiedener Stufen beschrieben. Neben einer Überschrift erster Stufe für den Seitentitel, die durch die Tags <h1> und </h1> markiert ist (Zeile 10), kommen auch auch Überschriften zweiter Stufe mit <h2> und </h2> als Abschnittstitel vor (Zeile 20 und 27).
<h1>Bandpage der Crispy Crablets</h1>
...
<h2>Die Band</h2>
...
<h2>Alben</h2>
...
Absätze:
Die Textabsätze sind durch die Tags <p> und </p> (für paragraph) markiert, siehe z. B. Zeile 11–19:
<p>
Text im ersten Absatz
</p>
<p>
Text im zweiten Absatz
</p>
<p>
Text im dritten Absatz
</p>
Liste:
Die Liste wird durch die Tags <ul> und </ul> (für unordered list) eingeleitet und abgeschlossen wird (Zeile 21 und 26), während die einzelnen Listeneinträge innerhalb der Liste durch die Tags <li> und </li> (für list item) gekennzeichnet sind (Zeile 22–25):
<ul>
<li>Erster Listeneintrag</li>
<li>Zweiter Listeneintrag</li>
<li>Dritter Listeneintrag</li>
<li>Vierter Listeneintrag</li>
</ul>
Wenn Sie die Beispiel-Webseiten durchstöbern, finden Sie auf den beiden Seiten, die über die Cover-Bilder verlinkt sind, weitere Listen, in denen die Einträge nummeriert dargestellt werden. Hier besteht der einzige Unterschied darin, dass die Liste durch die Tags <ol> und </ol> (für ordered list) beschrieben wird.
Betonter Text:
Daneben finden sich auch Auszeichnungen, um Textteile innerhalb von Absätzen zu betonen, z. B. die Tags <em> und </em> (für emphasized) zu Beginn des ersten Absatzes (Zeile 12):
Die <em>Crispy Crablets</em> sind eine Band aus ...
und die Tags <strong> und </strong> für den stark betonten Text zu Beginn des dritten Absatzes (Zeile 18):
<strong>Achtung:</strong> Hier findet ihr die aktuellen ...
Hyperlink:
Hyperlinks werden durch die Tags <a> und </a> (für anchor) markiert, wobei zwischen den Tags der “anklickbare” Seiteninhalt steht (siehe z. B. Zeile 18):
<a href="tour.html">Tourdaten</a>
Am Beispiel des Hyperlinks ist zu sehen, dass eine Auszeichnung auch zusätzliche Informationen enthalten kann – in diesem Fall wird die Ziel-URL, auf die der Hyperlink verweist, im öffnenden Tag nach href= angegeben (auf diesen Fall wird unter HTML-Attribute genauer eingegangen).
In allen Beispielen ist außerdem erkennbar, dass sich Textauszeichnungen unterscheiden lassen, die vom Browser als Absätze bzw. voneinander abgesetzte “Blöcke” innerhalb der Seite dargestellt werden (z. B. Überschriften, Textabsätze oder Listen, aber auch Tabellen oder Bilder), und Auszeichnungen für Textabschnitte, die im Fließtext dargestellt werden (z. B. betonte Textteile oder Hyperlinks im Text).
Außerdem finden sich noch weitere Tags außerhalb des eigentlichen Seiteninhalts im HTML-Dokument: So wird das Dokument selbst beispielsweise durch das Tag <html> eingeleitet (Zeile 2) und durch </html> abgeschlossen (Zeile 36). Im nächsten Abschnitt werden wir einen systematischen Blick auf die Grundstruktur von HTML-Dokumenten, sowie Syntax und Semantik der HTML-Tags werfen.
HTML-Dokumente
Zunächst fassen wir kurz zusammen, was wir anhand der Beispiel-Webseite gelernt haben: Ein HTML-Dokument beschreibt einen strukturierten Text, der unter anderem Überschriften, Absätze, Bilder, Listen und Tabellen sowie Hyperlinks enthalten kann. Dazu werden Textteile mit Tags ausgezeichnet, wodurch der Text in Elemente unterschiedlicher Bedeutung gegliedert wird. Die folgenden Abbildungen stellen die jeweiligen Abstraktionsstufen für das Beispiel grafisch dar:
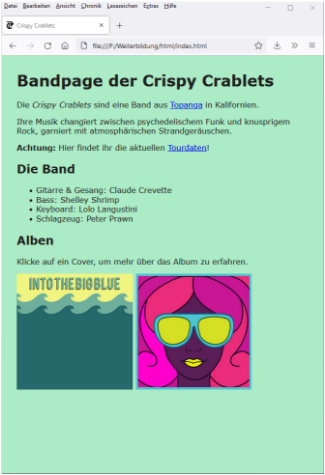





Grundgerüst
Eine HTML-Datei hat immer den folgenden grundlegenden Aufbau:
In der ersten Zeile steht die Dokumenttyp-Deklaration, die dem Browser die Art des Dokuments mitteilt. Die Angabe <!DOCTYPE html> sagt aus, dass es sich um ein HTML5-Dokument handelt.3
Das HTML-Dokument besteht immer aus zwei Teilen:
- dem Dokumentenkopf, der Informationen über das Dokument (“Metadaten”) enthält, z. B. den Titel der Seite oder die verwendete Zeichencodierung,
- dem Dokumentenrumpf, der die vom Browser dargestellten Seiteninhalte.
Dadurch hat jedes HTML-Dokument dasselbe Grundgerüst:
- Es beginnt mit dem Tag
<html>und endet mit dem Tag</html>. Diese Tags legen den gesamten dazwischenliegenden Dateiinhalt als HTML-Dokument fest. - Nach
<html>beginnt der Dokumentenkopf mit<head>und endet mit</head>. Dazwischen stehen die Metadaten, beispielsweise hier der Seitentitel (markiert durch die Tags<title>und</title>) und die Zeichencodierung des Dokuments (für HTML5 üblicherweise UTF-8). - Nach
</head>beginnt der Dokumentenrumpf mit<body>und endet mit</body>, direkt vor</html>. Dazwischen stehen die eigentlichen Seiteninhalte.
Die Informationen, die im Dokumentenkopf stehen, werden nicht innerhalb der Seite im Browser dargestellt, ggf. aber an anderer Stelle – der Seitentitel wird beispielsweise üblicherweise in der Kopfzeile des Browserfensters dargestellt, und im Dokumentenkopf lässt sich auch ein Symbolbild (“Favicon”) für die Webseite (z. B. für Lesezeichen) festlegen (siehe Weitere HTML-Elemente im Dokumentenkopf).
HTML-Elemente
Die durch Tags markierten Textteile – also die Einheiten aus öffnendem Tag, Inhalt und schließendem Tag – stellen die Grundbausteine dar, aus denen das HTML-Dokument zusammengesetzt ist und werden daher als HTML-Elemente bezeichnet. Dabei werden unterschiedliche Tag-Bezeichner verwendet, um verschiedene Typen von HTML-Elementen zu beschreiben – z. B. html für das Dokument an sich, body für den Dokumentenrumpf, p für einen Absatz oder a für einen Hyperlink.
Ein HTML-Element ist immer nach demselben Schema aufgebaut: Es beginnt mit einem öffnenden Tag der Form <Tag-Name>, gefolgt vom Inhalt des Elements, und wird durch ein schließendes Tag
der Form </Tag-Name> beendet. Der Inhalt kann dabei reiner Text sein, aber auch weitere HTML-Elemente enthalten – HTML-Elemente können also “ineinander verschachtelt” werden.
Daneben gibt es auch HTML-Elemente ohne Inhalt, die nur aus einem einzelnen Tag der Form <Tag-Name> bestehen. Beispielsweise stellt <br> ein einfaches HTML-Element ohne Inhalt dar, nämlich einen Zeilenumbruch im Fließtext.
Welche HTML-Elemente an welcher Stelle im HTML-Dokumente zulässig sind und auf welche Weise HTML-Elemente ineinander verschachtelt werden dürfen, wird dabei durch die HTML-Spezifikation geregelt (siehe Validierung von HTML). In vielen Fällen erschließen sich diese Regeln aber relativ intuitiv aus der Bedeutung der Elemente: So darf das HTML-Element <title>, das den Seitentitel angibt, nur im <head>-Element (also im Dokumentenkopf) stehen, während HTML-Elemente wie <h1> für Überschriften oder <p> für Textabsätze nur im <body>-Element (also im Seiteninhalt) erlaubt sind.Listeneinträge mit <li> machen dagegen nur innerhalb von Listen Sinn, also z. B. im Inhalt von <ol>-Elementen.
HTML-Attribute
Die meisten HTML-Elemente besitzen Attribute, über die bestimmte Eigenschaften für das Element festgelegt werden können. Bei einem Hyperlink-Element <a> gibt beispielsweise der Inhalt an, wie der Hyperlink im Browser dargestellt wird (hier durch den Text “Topanga”), während die Ziel-URL über ein Attribut namens href (kurz für hyperlink reference) festgelegt wird:
Die Zuweisung von Werten zu Attributen erfolgt immer im öffnenden Tag in der Form Attributname = Wert.
Für einige Attribute wie href muss ein Wert angegeben werden, damit das HTML-Element sinnvoll interpretiert werden kann. Andere Attribute sind optional – wenn kein Wert explizit zugewisen wird, wird ein Standardwert verwendet.
Ein weiteres Beispiel für HTML-Elemente mit Attributen (in diesem Fall ohne Inhalt) ist das HTML-Element <img>, mit dem sich Bilder in Webseiten einbinden lassen:
- Über das Attribut
srcwird die Quell-URL der Bilddatei angegeben. Für dieses Attribut muss ein Wert angegeben werden, während die folgenden Attribute optional sind. - Mit dem Attribut
widthkann die gewünschte Bildbreite zur Darstellung festgelegt werden. Ist das Bild größer oder kleiner, wird es vom Browser zur Darstellung entsprechend skaliert. Alternativ kann auch die gewünschte Bildhöhe mitheightfestgelegt werden. - Mit dem Attribut
altkann eine Bildbeschreibung als Alternativtext festgelegt werden, der statt des Bildes angezeigt wird, wenn das Bild nicht geladen werden kann. - Mit dem Attribut
titlekann ein Text festgelegt werden, der als “Popup” erscheint, wenn sich der Mauszeiger über dem Bild befindet.
HTML-Attribute sind also benannte Eigenschaften von HTML-Elementen, denen sich Werte zuweisen lassen, wodurch sich das Verhalten der HTML-Elemente genauer steuern lässt (ähnlich den Attributen von Scratch-Objekten in der Visuellen Programmierung). Welche Attribute welches Element besitzt, welche Werte für welche Attribute zulässig sind und was sie bedeuten, ist für jedes HTML-Element in der HTML-Spezifikation festgelegt und lässt sich auch in HTML-Referenzen wie z. B. bei W3Schools nachlesen.
URLs in Webseiten
Mit Hyperlinks und Bildern haben wir zwei HTML-Elemente kennengelernt, die Verknüpfungen zu anderen Dokumenten beschreiben. In beiden Fällen wird die Verknüpfung dadurch spezifiziert, dass die URL der verknüpften Datei als Wert für ein bestimmtes Attribut festgelegt wird (href bei Hyperlinks, src bei Bildern).
Hierbei muss zwischen zwei Arten von URL-Angaben unterschieden werden: absoluten URL-Angaben und relativen URL-Angaben. Betrachten Sie dazu die beiden Hyperlinks, die in der Beispiel-Webseite index.html vorkommen:
- Eine absolute URL wie beispielsweise
https://de.wikipedia.org/wiki/Topanga(Zeile 12) stellt eine vollständige Webadresse dar, die auf eine Datei im Internet verweist. - Eine relative URL wie beispielsweise
tour.html(Zeile 18) stellt dagegen eine Webadresse dar, die relativ zum Dateipfad auf dem Webserver angegeben ist, unter dem die Webseite erreichbar ist, in der diese URL verwendet wird.
Im zweiten Fall wird also erwartet, dass sich die Datei tour.html im selben Ordner auf dem Webserver befindet wie die Datei index.html, in welcher der Hyperlink mit dieser URLs vorkommt. Dasselbe gilt für die URLs der Bilddateien (Zeile 32–33), die ebenfalls im selben Verzeichnis liegen. Angenommen, die Bilder würden in einen Unterordner images verschoben werden. In diesem Fall müssten die URLs in den src-Attributen geändert werden zu “images/cover1.jpg” bzw. “images/cover2.jpg”.
Üblicherweise werden Verknüpfungen zu Dateien, die auf demselben Webserver liegen, in relativer Form angegeben, während Verknüpfungen zu Dateien, die auf anderen Webservern liegen in absoluter Form angegeben werden.
Vertiefung: Objektmodell
Da ein HTML-Dokument aus ineinander verschachtelten HTML-Elementen und Textelementen besteht, lässt sich seine Grundstruktur auch als Baumstruktur darstellen, in der jeder Knoten ein HTML-Element repräsentiert, z. B. eine Überschrift, einen Absatz oder einen Hyperlink. Die Kindknoten eines HTML-Elements sind dabei die Elemente, die in seinem Inhalt liegen. Das Element <html> repräsentiert dabei den Wurzelknoten, der genau zwei Kindknoten besitzt (<head> und <body>), die jeweils weitere, im Inhaltsteil auch beliebig tief weiterverzweigte Knoten enthalten. Auch Textteile, die als Inhalt von HTML-Elementen auftreten, stellen Knoten in diesem Baum dar.
Die HTML-Elemente (und Text-Elemente), aus denen ein HTML-Dokument besteht, lassen sich als Objekte im Sinne der Programmierung betrachten: Sie haben Attribute mit bestimmten Werten, durch die ihre Eigenschaften festgelegt werden, und stehen entsprechend der Baumstruktur in Beziehung zueinander. Im Webbrowser werden HTML-Dokumente intern tatsächlich auf diese Weise repräsentiert: Beim Lesen eines HTML-Dokuments wird im Speicher ein Baum von Objekten erzeugt, den der Browser zur Präsentation der Seite verwendet. Diese Darstellung wird auch als Document Object Model (kurz DOM, engl. für “Dokumenten-Objekt-Modell”) bezeichnet.4
Webseiten erstellen
Um eine einfache Website mit HTML zu erstellen, benötigen Sie nur einen Texteditor zum Bearbeiten der HTML-Dateien und einen Webbrowser zum Anzeigen der Seiten. Sie benötigen keinen Webserver, der Ihre Dateien über das Internet zur Verfügung stellt, sondern können die Dateien einfach lokal auf Ihrem Rechner speichern und bearbeiten.5
Legen Sie zunächst einen Ordner auf Ihrem Rechner an, in dem Sie die HTML-Dateien und andere Dateien (z. B. Bilder) für Ihre Website speichern. Erstellen Sie dort eine neue Textdatei mit der Dateiendung .html (zum Beispiel homepage.html oder index.html6), öffnen Sie sie im Texteditor und fügen Sie das Grundgerüst als Inhalt ein (den Seitentitel können Sie durch einen eigenen, passenden Titel ersetzen):
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Seitentitel</title>
</head>
<body>
</body>
</html>
Achten Sie darauf, dass UTF-8 als Zeichencodierung verwendet wird. Alternativ können Sie die HTML-Datei homepage.html mit dem Grundgerüst auch hier als Vorlage herunterladen und in Ihrem Arbeitsordner speichern: Download
Im Dokumentenrumpf können Sie nun eigenen Inhalt ergänzen, zum Beispiel Überschriften und Textabsätze. Eine Überblick über grundlegende HTML-Elemente, die Ihnen beim Erstellen erster eigener Webseiten helfen können, finden Sie im Anhang unter HTML-Referenz.
Öffnen Sie die Datei nun in einem Webbrowser, um die grafische Darstellung der Seite präsentiert zu bekommen.
Generell ist es bei der Entwicklung von Webseiten im Texteditor hilfreich, sowohl den Editor als auch die Browseransicht gleichzeitig in zwei nebeneinander auf Ihrem Desktop positionierten Fenstern geöffnet zu haben, damit Sie Änderungen an der Textdatei schnell visuell überprüfen können. Speichern Sie dazu nach einer Änderung die Textdatei und aktualisieren Sie dann die Browseransicht der Webseite (z. B. in Firefox die Taste F5 drücken).
Wenn Sie Verknüpfungen zu anderen Webseiten oder Bildern erstellen, die in Ihrem Arbeitsordner liegen, reicht als URL der Dateiname. Wenn Sie beispielsweise ein Bild in eine Webseite einfügen möchten, das in einer Datei leuchtturm.jpg gespeichert ist, kopieren Sie die Datei den Ordner, in dem auch die entsprechende HTML-Datei liegt, und fügen Sie ein HTML-Element <img> zum Seiteninhalt hinzu, z. B.:
<img src="leuchtturm.jpg" alt="Bild eines Leuchtturms">
Als umfangreicheres Beispiel können Sie auch die Beispiel-Website aus der Einleitung auf Ihren Rechner herunterladen, untersuchen und verändern: Download
Entwicklungsumgebungen
Prinzipiell können Sie jeden einfachen Texteditor, der auf Ihrem Rechner installiert ist, zur Bearbeitung von HTML-Dateien verwenden. Einige Texteditoren sind aber geeigneter als andere, da sie über nützliche Funktionen zur HTML-Bearbeitung verfügen.
Die meisten Texteditoren verwenden Syntax Highlighting für HTML, heben also spezielle HTML-Bestandteilen wie Tags, Attributnamen oder -werte im Text durch spezielle Farben oder Formatierungen hervor, was die Übersichtlichkeit des Quelltextes erhöht.
Einige Texteditoren beherrschen darüber hinaus Code-Vervollständigung, dass heißt, dass sie während der Eingabe Vorschläge zur Textergänzung machen, wenn Sie HTML-Code erkennen, zum Beispiel:
- Wenn Sie
<seingeben, erscheint eine Liste, in der alle Tag-Namen, die mit “s” beginnen, ausgewählt werden können. - Wenn Sie
<agefolgt von einem Leerzeichen eingeben, erscheint eine Liste, in der alle Attribute des Elements ausgewählt werden können. - Wenn Sie das Tag
<h1>eingegeben haben, erscheint automatisch das dazu passende schließende Tag</h1>.
Fortgeschrittenere Editoren enthalten manchmal auch eine integrierte Browservorschau, die während der Eingabe automatisch aktualisiert wird, so dass Sie den visuellen Effekt einer Änderung im Quelltext sofort überprüfen können.
Eine Liste von Texteditoren mit solchen Funktionen finden Sie in der Linksammlung bei den Software-Werkzeugen. Für Windows ist Notepad++ aufgrund seiner Einfachheit empfehlenswert. Unter Linux und iOS verfügt der vorinstallierte Standard-Texteditor in der Regel bereits über Syntax Highlighting und Code-Vervollständigung für HTML.
Online-Editoren
Daneben finden Sie im Internet auch eine Reihe von Online-Entwicklungsumgebungen für kleinere HTML-Projekte, die einfach im Webbrowser geöffnet werden können und nicht auf Ihrem Rechner installiert werden müssen. Diese Tools besitzen in der Regel eine integrierte Browservorschau und ermöglichen es zum Teil auch, online auf die erstellten Websites zuzugreifen – das heißt, sie können von anderen Personen im Webbrowser geöffnet werden, statt nur lokal auf Ihrem Rechner verfügbar zu sein.
Die E-Learning-Webseite W3Schools stellt beispielsweise für ihre HTML/CSS-Tutorials einen sehr einfachen Online-Editor zum Bearbeiten und Anzeigen einzelner HTML-Seiten bereit.
In der Online-Entwicklungsumgebung Glitch lassen sich Websites erstellen, die aus mehreren HTML-Seiten sowie weiteren Dateien (z. B. Bilder, CSS-Dateien) bestehen. Die erstellten Websites können über einen öffentlichen Link von jedem angesehen und “remixt” werden, so dass sich Glitch auch im Rahmen des Schulunterrichts zum Bereitstellen von Webseiten eignet, die durch die Schülerinnen und Schüler angepasst, korrigiert oder erweitert werden sollen.
Sie finden Links zu Glitch und weiteren Online-Editoren in der Linksammlung bei den Software-Werkzeugen.
HTML-Inspektoren
Im Aufbau
Validierung
Damit HTML-Dokumente sinnvoll interpretiert werden können, müssen sie logisch und strukturell korrekt sein. Wie korrekter HTML-Quellcode aussieht, ist dabei durch Spezifikationen7 der Hypertext Markup Language festgelegt. HTML-Quellcode, der sich an alle Konventionen und Spezifikationen hält, wird als valide bezeichnet, die Überprüfung als Validierung.
Die offiziellen Spezifikationen für HTML werden vom World Wide Web Consortium (W3C) und der Web Hypertext Application Technology Working Group (WHATWG) entwickelt.8 Darin wird unter anderem festgelegt:
- welche Grundstruktur ein valides HTML-Dokument hat,
- welche Attribute für bestimmte HTML-Elemente erlaubt sind,
- welche Attribute optional sind und welche zwingend benötigt werden,
- welche HTML-Elemente innerhalb von welchen anderen HTML-Elemente erlaubt sind,
- welche HTML-Elemente und -Attribute veraltet sind und nicht mehr genutzt werden sollten,
- wie ein Webbrowser HTML-Elemente mit bestimmten Eigenschaften interpretieren sollte.
Dabei gibt es Unterschiede zwischen verschiedenen Versionen von HTML. Die HTML-Version eines HTML-Dokuments wird durch die Angabe des Dokumenttyp mit <!DOCTYPE …> zu Beginn festgelegt.
Ein valides HTML-Dokument besteht immer aus der Dokumenttyp-Deklaration und den Elementen <html>, <head>, <title> und <body> (siehe Grundgerüst).
Beispiele für eine valide Struktur von HTML-Elementen im Seiteninhalt sind etwa:
- Listeneinträge (
<li>) nur innerhalb von Listen (<ul>,<ol>) vorkommen dürfen, - innerhalb eines Paragraphen (
<p>) keine gruppierenden Elemente wie Listen (<ul>,<ol>) vorkommen dürfen.
Beispiele für grundlegende Vorgaben, wie Webbrowser mit HTML-Elementen umzugehen haben, sind:
- Das Ziel eines Hyperlinks (
<a>) soll in einem neuen Fenster geöffnet werden, wenn das Attributtargetden Wert"_blank"hat. - Für ein Bild (
<img>) soll dessen Alternativtext (Wert des Attributsalt) angezeigt werden, wenn das Bild nicht geladen werden konnte.
So können sich Webentwicklerinnen und -entwickler darauf verlassen, dass ihre HTML-Dokumente auf eine vorgegebene Weise von Webbrowsern interpretiert und dargestellt werden, solange sie sich an die entsprechenden Vorgaben halten.
Die meisten Webbrowser können HTML-Dokumente aber auch dann einigermaßen sinnvoll darstellen, wenn der HTML-Quellcode nicht vollständig valide ist, also in einem gewissen Umfang logische oder strukturelle Fehler enthält. In solchen Fällen ist aber nicht gesichert, ob die Seite wie erwartet dargestellt wird, weswegen solche Fehler in der Praxis möglichst vermieden werden sollten. Typische Fehler sind:
- Ein öffnendes Tag wird an der falschen Stelle oder gar nicht geschlossen.
- Ein Element, das in den Inhaltsbereich (
<body>) gehört, wird versehentlich im Kopf der HTML-Datei (<head>) definiert. - Die Namen von Tags oder Attributen enthalten Buchstabendreher oder andere Schreibfehler.
Tipp: Um Fehler schneller zu finden, ist es sinnvoll, HTML-Quelltext übersichtlich zu strukturieren. Die folgende Abbildung zeigt sehr chaotischen Quelltext, in dem es schwer ist, die vorhandenen Fehler ausfindig zu machen (links). In der aufgeräumten Version (rechts) lässt sich dagegen schnell feststellen, dass zwei schließende Tags fehlen bzw. syntaktisch falsch angegeben sind:

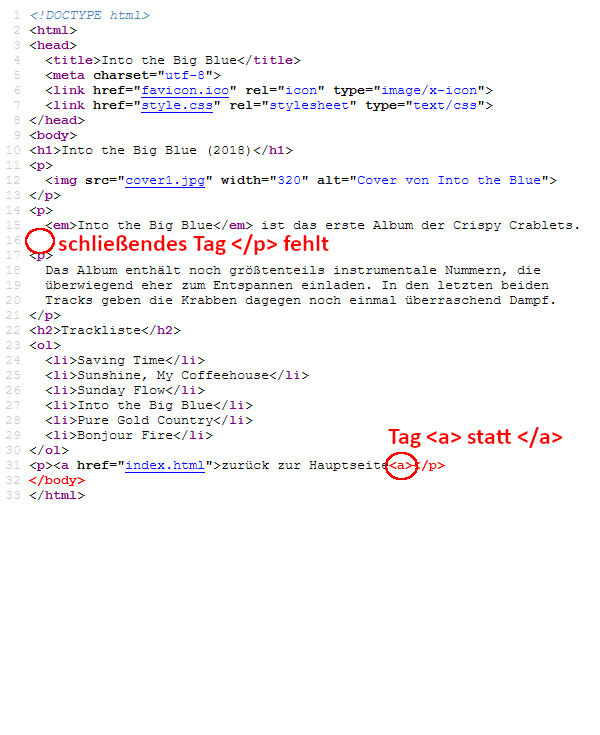
W3C Online-Validator
Tool: Um zu überprüfen, ob ein HTML-Dokument valide ist, kann der Online-Validator des W3C verwendet werden: https://validator.w3.org
In diesem Tool kann eine HTML-Datei hochgeladen, die URL einer HTML-Datei im Internet eingegeben oder HTML-Quellcode in ein Texteingabefeld eingefügt werden und validiert werden. Erkannte Fehler und Warnungen werden anschließend angezeigt.
Die folgende Abbildung zeigt, wie HTML-Quellcode über das Texteingabefeld validiert wird (links), wobei ein schließendes Tag fehlt. Nachdem auf die Schaltfläche “Check” geklickt wird, erscheint ein Validierungsbericht (rechts), in dem als Fehler das fehlende Tag <\h1> (3.), sowie zwei Folgefehler (1. und 2.) erkannt werden:
- Da das Tag
<h1>nicht geschlossen wird, wird das folgende Absatz-Element<p>als Kindknoten des Überschrift-Elements<h1>interpretiert, was aber laut HTML-Spezifikation nicht erlaubt ist. - Es wird erkannt, dass beim Schließen des
<body>-Tags innerhalb des Dokumentenrumpfes Elemente vorkommen, die noch nicht geschlossen wurden (nämlich<h1>).
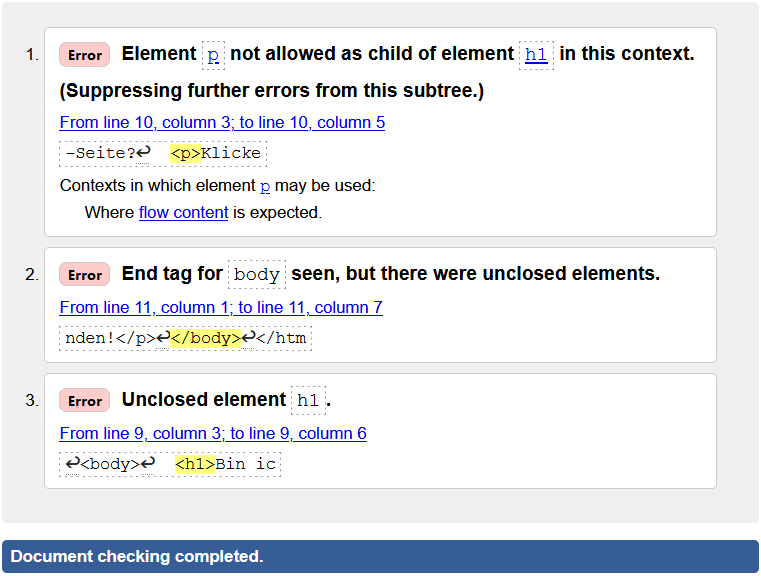
HTML-Referenz
Hier finden Sie einen kurzen Überblick über die wichtigsten, grundlegenden HTML-Elemente zum Erstellen einfacher Webseiten, jeweils nach Kategorien aufgeteilt. Umfangreichere Listen zum Weiterlernen finden Sie bei W3Schools und SELFHTML.
Dokument
Diese HTML-Elemente legen die Grundstruktur des HTML-Dokuments fest.
| Element | Beschreibung |
|---|---|
<html> </html> |
HTML-Dokument |
<head> </head> |
Dokumentenkopf mit Metadaten, z. B. Titel der Seite |
<body> </body> |
Dokumentenrumpf mit Seiteninhalt |
Text
Diese HTML-Elemente dienen zur Textgliederung und Auszeichnung von Textteilen im Seiteninhalt.
| Element | Beschreibung |
|---|---|
<h1> </h1> … <h6> </h6> |
Überschriften (Stufe 1 bis 6) |
<p> </p> |
Textabsatz (Paragraph) |
<br> |
Zeilenumbruch (engl. break line) |
<hr> |
Horizontale Trennlinie (engl. horizontal ruler) |
<em> </em> |
Betonter Text (engl. emphasized), in der Regel kursiv dargestellt9 |
<strong> </strong> |
Stark betonter Text, in der Regel fett dargestellt10 |
<code> </code> |
Quellcode, in der Regel mit Festbreitenschrift dargestellt11 |
<q> </q> |
Zitat im Fließtext |
<blockquote> </blockquote> |
Zitat als Absatz |
Verknüpfungen
Diese HTML-Elemente dienen zum Verknüpfen von Webseiten untereinander und zum Einfügen von Bilddateien in den Seiteninhalt. Die URLs und weitere (optionale) Informationen werden über die Attribute der Elemente festgelegt.
| Element | Beschreibung | Attribute | Beschreibung |
|---|---|---|---|
<a href="URL"> </a> |
Hyperlink | href="URL" |
legt das Ziel der Verknüpfung fest |
optional: target="_blank" |
legt fest, dass das Ziel in einem neuen Fenster geöffnet werden soll | ||
<img src="URL"> |
Bild | src="URL" |
legt die URL der Bilddatei fest |
optional: Attributen alt="Text" |
legt Alternativtext fest, der angezeigt wird wenn das Bild nicht geladen werden konnte | ||
optional: width="Zahl" und/oder height="Zahl" |
legt die gewünschte Bildgröße zur Darstellung fest | ||
optional: title="Text" |
legt Beschreibungstext fest, der beim Draufzeigen mit der Maus angezeigt wird |
Listen und Tabellen
Listen und Tabellen im Seiteninhalt werden durch verschachtelte HTML-Elemente beschrieben.
| Element | Beschreibung |
|---|---|
<ul> </ul> |
Liste ohne Nummerierung |
<ol> </ol> |
Nummerierte Liste |
<li> </li> |
Listeneintrag innerhalb einer Liste (innerhalb <ul> oder <ol>) |
<table> </table> |
Tabelle |
<tr> </tr> |
Tabellenzeile in einer Tabelle (innerhalb <table>) |
<td> </td> |
Datenzelle in einer Tabellenzeile (innerhalb <tr>) |
<th> </th> |
Spaltenüberschrift in einer Tabellenzeile (innerhalb <tr>), in der Regel die Datenzellen der ersten Tabellenzeile |
Die Art der Nummerierung für die Listeneinträge in einem <ol>-Element kann durch das HTML-Attribut ``
Metadaten
Die folgenden HTML-Elemente legen Informationen über das Dokument fest und kommen nur im Dokumentenkopf vor.
| Element | Beschreibung |
|---|---|
<link> |
Externe Datei im Dokumentenkopf einbinden mit Attributen href="URL" zum Festlegen der Quelle und rel=Relation für die Bedeutung der externen Datei, z. B. rel="stylesheet" für eine CSS-Datei oder rel="icon" für das Favicon12 |
<meta> |
Weitere Metadaten, z. B. <meta charset="utf-8"> zum Festlegen der Zeichencodierung als UTF-8 |
Vertiefung: HTML-Entities
Da im HTML-Quellcode bestimmte Zeichen eine Sonderbedeutung haben – insbesondere die spitzen Klammern < und >, die zur Kennzeichnung von Tags verwendet werden – müssen solche Zeichen auf eine andere Weise dargestellt werden, wenn sie im Seiteninhalt als Textzeichen vorkommen sollen.
Beispiel:
Angenommen, der HTML-Quellcode enthält die folgende Zeile, in der die Bedeutung des HTML-Elements <em> erläutert wird:
<p>Das Tag <em> betont Text und wird durch das Tag </em> geschlossen.</p>
Der entsprechende Absatz wird vom Browser aber folgendermaßen dargestellt, da die Zeichenfolgen <em> und </em> natürlich als HTML-Tags interpretiert werden:
Das Tag betont Text und wird durch das Tag geschlossen.
Um solche Sonderzeichen als reine Textzeichen darzustellen, werden in HTML bestimmte alternative Zeichenfolgen verwendet, die sogenannten HTML-Entities. Diese werden in der Form &Entity-Name; angegeben, wobei die Entity-Namen meistens Kurzformen der repräsentierten Zeichen darstellen. Die HTML-Entities für die Zeichen < und > sind beispielsweise < (kurz für less than = kleiner gleich) und > (kurz für greater than = größer gleich).
Da das Zeichen & eine HTML-Entity einleitet, muss dieses ebenfalls durch eine HTML-Entity ersetzt werden, wenn es als Textzeichen dargestellt werden soll – in diesem Fall durch die Zeichenfolge & (kurz für ampersand = “Kaufmanns-Und”).
HTML-Entities existieren für viele Sonderzeichen, auch für solche, die in HTML keine Sonderbedeutung haben. Das ist hilfreich für Steuerzeichen, die sich nicht direkt per Tastatur eingeben lassen, beispielsweise das geschützte Leerzeichen (kurz für non-breaking space) oder das weiche Trennzeichen ­ (kurz für soft hyphen).13
Alternativ lässt sich jedes Sonderzeichen in HTML auch im Format &#Nummer; mit der Unicode-Nummer des gewünschten Zeichens angeben, z. B. Ä für den Buchstaben Ä.
Die Definition von HTML-Entities ist hauptsächlich dadurch motiviert, dass HTML-Dateien früher in 8-Bit-Zeichencodierungen (in der Regel ISO-8859-1) codiert wurden. Seitdem sich HTML5 als Standard für HTML-Dokumente etabliert hat, wird standardmäßig UTF-8 als Zeichencodierung empfohlen, weswegen HTML-Entities in HTML5-Dokumenten bis auf wenige Ausnahmen kaum noch verwendet werden.
Die folgende Liste zeigt der Vollständigkeit halber einige der vor HTML5 am häufigsten verwendeten HTML-Entities:14
| HTML-Entity | Sonderzeichen |
|---|---|
Ä ä … ü |
Umlaute Ä ä … ü |
ß |
Eszett-Zeichen ß |
& |
Und-Zeichen & (engl. ampersand) |
< > |
Spitze Klammern < > (bzw. Vergleichszeichen, engl. less/greater than) |
" |
Anführungszeichen " (engl. quotation mark) |
° |
Grad-Zeichen ° (engl. degree) |
€ |
Euro-Zeichen € |
© |
Copyright-Zeichen © |
|
Geschütztes Leerzeichen (engl. non-breaking space) |
­ |
Weiches Trennzeichen (engl. soft hyphen) |
&#Nummer; |
Sonderzeichen mit der angegebenen Referenznummer (dezimal angegeben) |
&#xNummer; |
Sonderzeichen mit der angegebenen Referenznummer (hexadezimal angegeben) |
-
Formale Sprachen, die dieses Grundkonzept verwenden und zu denen auch HTML gehört, heißen daher “Auszeichnungssprachen” (markup languages). ↩︎
-
Generell empfielt es für den Einstieg in HTML, spezielle didaktisch reduzierte Webseiten zu untersuchen. Die meisten “echten” Webseiten eignen sich eher nicht als Lernbeispiele, da sie sehr umfangreichen, oft automatisch generierten und damit sehr unübersichtlichen HTML-Code enthalten. ↩︎
-
Wird die Dokumenttyp-Deklaration weggelassen, wird die Webseite zwar in der Regel trotzdem im Webbrowser angezeigt, eventuell aber nicht wie erwartet, da der Webbrowser in dem Fall die verwendete HTML-Version raten muss. ↩︎
-
Der Begriff HTML DOM bedeutet konkret nicht nur die Darstellung der HTML-Dokuments durch einen Baum von Objekten, sondern beschreibt darüber hinaus eine Programmierschnittstelle, die von Programmiersprachen wie JavaScript genutzt werden, um im Browser geladene HTML-Dokumente dynamisch zu ändern. ↩︎
-
So ist Ihre Website zwar nicht über das Internet von außen zugänglich, sondern kann nur lokal auf Ihrem Rechner geöffnet werden – für den Anfang reicht das aber, um erste Projekte zu erstellen, anhand derer sich HTML praktisch erlernen lässt. ↩︎
-
Der Dateiname index.html wird üblicherweise für die Einstiegsseite einer Website verwendet, die aus mehreren HTML-Dateien besteht. ↩︎
-
Eine Spezifikation im Sinne der Informatik legt die Eigenschaften und die gewünschte Umsetzung einer Technologie (z. B. einer Software, einer Programmiersprache, eines technischen Systems) fest. ↩︎
-
siehe https://www.w3.org/TR/html5 und https://html.spec.whatwg.org ↩︎
-
vgl.
<i> </i>für kursiv dargestellten Text (engl. italic) ↩︎ -
vgl.
<b> </b>für fettgedruckten Text (engl. bold) ↩︎ -
vgl.
<tt> </tt>für Text mit Festbreitenschrift (Schreibmaschinen- oder Fernschreiberschrift, engl. teletype) ↩︎ -
Ein Favicon (engl. favorite icon) ist ein kleines Symbolbild für eine Webseite, das im Browser oben neben dem Seitentitel und im Lesezeichenmenü angezeigt wird. ↩︎
-
Eine Zeile wird bei einem geschützten Leerzeichen nicht umgebrochen, außerdem ersetzt der Webbrowser mehrfache aufeinanderfolgende geschützte Leerzeichen nicht durch ein einzelnes Leerzeichen, wie bei normalen Leerzeichen im HTML-Quelltext. Eine weiches Trennzeichen wird dagegen nur dargestellt, wenn das Wort an dieser Stelle durch einen Zeilenumbruch getrennt wird. ↩︎
-
siehe auch Listen bei W3Schools und SELFHTML. Eine vollständige Liste aller HTML-Entity-Namen des W3C finden Sie hier:
https://html.spec.whatwg.org/multipage/named-characters.html#named-character-references ↩︎
2.3.2 Gestaltung mit CSS
Mit HTML lässt sich die Struktur von Webseiten definieren und Textinhalte können semantisch ausgezeichnet werden, z. B. als Hyperlinks, betonter Text, Code oder Zitat. Wie diese Elemente grafisch dargestellt werden, hängt dabei vom Webbrowser ab, also beispielsweise welche Schriftart für Überschriften, Textinhalte oder Code jeweils verwendet wird oder mit welcher Hintergrundfarbe die Seite dargestellt wird.
Als Beispiel ist hier eine Webseite zu sehen, die ohne jede Gestaltungsvorgaben in den Browsern Firefox und Opera angezeigt wird.
 |
 |
|---|
Die grafische Darstellung kann also je nach Webbrowser und Betriebssystem unterschiedlich sein (z. B. werden hier üblicherweise verschiedene Standardschriftarten verwendet). Dabei gibt es Konventionen, die von den meisten Webbrowser eingehalten werden, z. B. wird <em> kursiv dargestellt, <strong> fett, <code> mit einer Festbreitenschriftart, Unterschriften höherer Ebenen größer als Unterschriften niedrigerer Ebenen. Davon abgesehen lässt sich mit reinem HTML bisher aber kein Einfluss auf die grafische Gestaltung der Seite nehmen.
Wie Elemente einer HTML-Webseite dargestellt werden sollen, wird durch eine andere Sprache beschrieben, nämlich CSS.
CSS
CSS steht kurz für Cascading Style Sheets (also etwa “gestufte Gestaltungsbögen”) und stellt eine formale Sprache dar, mit der sich die grafische Darstellung von HTML-Elementen in textueller Form beschreiben lässt. Dazu werden zusätzliche Attribute verwendet, die als Stilattribute (oder CSS-Attribute) bezeichnet werden.
In einem CSS-Dokument wird beschrieben, wie HTML-Elemente dargestellt werden sollen, indem ihren Stilattributen bestimmte Werte zugewiesen werden. Solche Wertezuweisungen für ein bestimmtes Element werden als Stilregeln (oder CSS-Regeln) bezeichnet. Diese Regeln stellen Gestaltungsanweisungen für den Browser dar.
Ähnliche Stilregeln kennen wir aus akademischen Kontexten, wenn es etwa um die Ausfertigung von schriftlichen Arbeiten geht. Beispielsweise heißt es in §11 APVO Lehrkräfte über die schriftliche Hausarbeit im Rahmen des Vorbereitungsdienstes:
Die Schriftart ist Arial mit dem Zeilenabstand 1,0; der Schriftgrad beträgt 12 Pt.
In CSS formuliert könnte diese Stilregel so aussehen:
body {
font-family: Arial;
line-height: 1.0;
font-size: 12pt;
}
Das CSS-Dokument wird mit dem HTML-Dokument verknüpft, indem im Dokumentenkopf des HTML-Dokuments ein entsprechendes <link>-Element angegeben wird:
Verwechslungsgefahr! Das <link>-Element dient nicht dazu, Links auf andere Seiten zu setzen! Dafür muss der Tag <a> verwendet werden. Das <link>-Element verknüpft mehrere Dateien, die zusammengesetzt eine Webseite ergeben.
<head>
...
<link href="style.css" rel="stylesheet" type="text/css">
</head>
In diesem Fall heißt die CSS-Datei style.cssund liegt im selben Verzeichnis auf dem Webserver wie die HTML-Seite, von der sie verwendet wird.
Dieses Prinzip erlaubt es, ein und die selbe CSS-Datei in allen HTML-Dateien einer Website einzubinden, so dass die Gestaltungsregeln der gesamten Website an einer zentralen Stelle festgelegt werden können.
CSS-Regeln
Eine CSS-Regel ist immer nach demselben Schema aufgebaut: Sie beginnt mit einer Angabe, für welche(s) HTML-Element(e) die Regel gelten soll. Dieser Teil der Regel wird als Selektor bezeichnet. Es folgen in geschweiften Klammern die Wertezuweisungen zu den Stilattributen, jeweils im Format: Attributname Doppelpunkt Wert(e) Semikolon
Als Selektor kann ein einzelnes HTML-Element oder mehrere HTML-Elemente durch Komma getrennt angegeben werden, für welche die Stilregel gelten soll.
Die meisten Stilattribute erwarten einen einzelnen Wert, der zum erwarteten Datentyp passen muss. Die für den Einstieg relevanten Datentypen, die in CSS unterschieden werden, sind:
- Farbwerte: z. B. für Schriftfarben, Linien- und Hintergrundfarben von HTML-Elementen (siehe Referenz zu Farbwerten)
- Größenangaben: z. B. für Abstände, Schriftgrößen oder Linienbreiten von HTML-Elementen (siehe Referenz zu Größenangaben)
- Schriftarten: z. B. für das Attribut
font-family, werden durch die Namen der Schriftarten durch Komma getrennt beschrieben - Aufzählungen: Attribut-spezifische Bezeichner, z. B. kann für das Attribut
text-alignals Textausrichtungleft,right,centeroderjustify(Blocksatz) angegeben werden - Zahlenwerte (Ganzzahlen, Dezimalzahlen) und Prozentangaben: z. B. auch für Größenangaben
Es gibt auch Stilattribute, die mehrere Werte (durch Leerzeichen getrennt) erwarten – diese Attribute sind meistens Kurzformen, die mehrere andere Attribute zusammenfassen. Beispielsweise gibt es die Stilattribute border-width, border-style und border-color, mit denen sich jeweils die Breite, der Linienstil (z. B. durchgezogen, gestrichelt) und die Farbe für den Rahmen eines HTML-Elements festlegen lässt:
table {
border-width: 1px;
border-style: solid;
border-color: black;
}
Daneben gibt es ein Attribut border, mit dem sich in Kurzform alle drei Werte auf einmal zuweisen lassen. Die Werte werden dabei in der Reihenfolge Breite Stil Farbe erwartet:
table {
border: 1px solid black;
}
Selektoren
CSS erlaubt es, durch die Angabe von speziellen Selektoren sehr präzise zu definieren, für welche Elemente spezielle Gestaltungsregeln gelten sollen.
Der universelle Selektor * erlaubt es, Regeln für alle HTML-Elemente der Seite festzulegen, z.B. um Standardschriftarten zu definieren:
* {
font-family: "Libertinus Serif";
}
Tags
Der Name eines Tags kann einfach so, ohne die spitzen Klammern, als Selektor verwendet werden. Sofern keine anderen Regeln das einschränken, gelten diese Regeln dann für alle Elemente dieses Tags.
h1 {
/* Regeln für alle Überschriften auf Ebene 1 */
}
img {
/* Regeln für alle Bilder */
}
Klassen und IDs
Mit dem HTML-Attribut class können HTML-Elemente zu so genannten Klassen hinzugefügt werden. Diese Klassen können dann genutzt werden, um z. B. für manche Absätze separate Regeln festzulegen. Wenn eine Klasse als Selektor verwendet wird, muss vor ihren Namen ein Punkt gesetzt werden.
Stellen wir uns als Beispiel ein Schulbuch vor, das neben normalem Text noch Infokästen und Hilfestellungen enthält. Das alles sind normale Textabsätze, die mit <p>-Tags gekennzeichnet werden. Die Infokästen werden dann als <p class="infokasten">...</p> und die Hilfestellungen als <p class="hilfestellung">...</p> aufgeschrieben. Die CSS-Regeln dazu könnten dann so aussehen:
.infokasten {
border: 1px solid black;
padding: 10px;
}
.hilfestellung {
border-left: 5px solid #feef00;
padding-left: 10px;
background-color: #feef0080;
}
HTML-Elemente können auch zu mehreren Klassen gehören. Die Klassennamen werden dann mit Leerzeichen getrennt in ein class-Attribut geschrieben:
<a class="external email" href="mailto:mail@example.org">Schreib mir eine E-Mail</a>
Genauso wie Klassen können auch IDs vergeben werden, diese kennzeichnen aber einzelne HTML-Elemente, während Klassen in der Regel mehrere Elemente umfassen. Das entsprechende HTML-Element wird mit dem Attribut id versehen und die ID als CSS-Selektor mit einer vorangestellten Raute markiert:
#seitenmenue {
background-color: lightblue;
color: navy;
}
Selektoren kombinieren
Um eine Regel für mehrere Selektoren gelten zu lassen, können diese mit Kommata separiert werden:
/* Überschriften erster bis dritter Ordnung werden unterstrichen. */
h1, h2, h3 {
text-decoration: underline;
}
/* i-Tags, em-Tags und Elemente der Klasse "notice" werden kursiv dargestellt. */
i, em, .notice {
font-style: oblique;
}
Ineinandergeschachtelte HTML-Elemente können gezielt addressiert werden, indem die Selektoren von außen nach innen mit Leerzeichen getrennt aneinandergehängt werden:
/* Bilder in Infokästen dürfen maximal 30 % von dessen Breite ausfüllen. */
.infokasten img {
max-width: 30%;
}
/* Links in Überschriften werden doppelt unterstrichen. */
h1 a {
text-decoration: underline double;
}
Die Schnittmenge von einem Tag und einer Klasse kann addressiert werden, indem man den Selektor der Klasse direkt hinter den des Tags schreibt, ohne trennendes Leerzeichen:
/* Alle <p class="example">-Elemente */
p.example {
/*...*/
}
/* Alle <_ class="example">-Elemente innerhalb von <p>-Elementen */
p .example {
/*...*/
}
/* Alle <p>-Elemente und alle <_ class="example">-Elemente */
p, .example {
/*...*/
}
Layout
Abstände und Rahmen
Abstände und Rahmen werden in CSS mit dem so genannten Box-Modell erzeugt. Um jedes HTML-Element sind drei konzentrische Boxen angeordnet. Diese sind, von innen nach außen:
padding, der Abstand zwischen dem Rahmen und dem Element selbstborder, der Rahmenmargin, der Abstand um den Rahmen herum
Für padding und margin kann jeweils nur die Größe der Box angegeben werden, für border zusätzlich zur Rahmenbreite auch ein Linienstil (etwa solid für durchgezogen, dashed für gestrichelt oder dotted für gepunktet).
Zu beachten ist, dass alle diese drei Boxen unabhängig voneinander definiert werden können.
Diese Attribute können auf unterschiedliche Weisen verwendet werden. Die folgende Regel sorgt beispielsweise dafür, dass innerhalb von Tabellenzellen zehn Pixel Abstand zwischen der Rahmenlinie und dem Text bleiben.
td {
padding: 10px;
}
Statt nur einen Parameter anzugeben, der auf alle vier Seiten der Box angewendet wird, können auch vier Parameter angegeben werden, die in dieser Reihenfolge die Größen für die obere, rechte, untere und linke Seite der Box vorgeben:
h2 {
margin: 2.5rem 0 1.5rem 0;
}
Diese Gestaltungsregel wird übrigens auch hier in diesem Skript angewendet.
Statt die vier Parameter hintereinander anzugeben, können mit den Zusätzen -top, -bottom, -left und -right auch separate Regeln für die einzelnen Seiten einer Box definiert werden:
p {
border-top: 30px solid red;
margin-bottom: 0;
}
Seiten-Layout
Der Abschnitt “Seiten-Layout” befindet sich noch im Aufbau.
HTML-Elemente für Layout
| Element | Beschreibung |
|---|---|
<span> </span> |
Allgemeiner Container für Textbereiche ohne besondere Bedeutung |
<div> </div> |
Allgemeiner Container für Inhalte (engl. division element), in der Regel als Block dargestellt |
<header> </header> |
Container für den Kopfbereich einer Seite (z. B. Logo, Titel) |
<nav> </nav> |
Container für die Navigationsleiste einer Seite |
<main> </main> |
Container für den Hauptinhalt einer Seite |
<aside> </aside> |
Container für eine Seitenleiste neben dem Hauptinhalt (z. B. Menü) |
<footer> </footer> |
Container für die Fußzeile einer Seite (z. B. Link zum Impressum) |
Textgestaltung
Für die Textgestaltung ließe sich auch einfaches HTML nutzen – Tags wie <b> für Fettdruck, <font> zur Änderung von Schriftart, -größe und -farbe oder <sup> für hochgestellten Text existieren und werden in den meisten Browsern korrekt dargestellt. Wenn Sie eine Kapitelüberschrift in 16pt großer “Comic Sans”-Schriftart, fett und unterstrichen darstellen möchten, können Sie einfach die Tag-Kombination <font size="16pt" face="Comic Sans" color="blue"><b><u> ... </u></b></font> verwenden.
Das geht aber nur so lange gut, bis Sie diese Formatierung regelmäßig benutzen oder gar ändern möchten. Stattdessen empfiehlt es sich, diese Textteile zu einer Klasse zusammenzufassen und für diese Klasse Gestaltungsregeln in CSS festzulegen.
Aus <font size="16pt" face="Comic Sans" color="blue"><b><u> ... </u></b></font> wird dann z. B. <span class="kapitelueberschrift"> ... </span> mit der dazugehörigen CSS-Regel:
.kapitelueberschrift {
font-family: Comic Sans;
font-size: 16pt;
font-weight: bold;
text-decoration: underline;
}
Möchten Sie nun die Farbe der Kapitelüberschrift ändern, müssen Sie nicht mehr den HTML-Code an sechzehn Stellen anpassen, sondern nur den CSS-Code an einer.
Die CSS-Stilattribute für Textgestaltung lassen sich in zwei Kategorien unterteilen: diejenigen für die Formatierung, die das Aussehen eines ganzen Textteils ändern, deren Namen üblicherweise mit text- beginnen, und diejenigen für die Schriftart, die das Aussehen der einzelnen Zeichen verändern, deren Namen üblicherweise mit font- beginnen.
Textformatierung
In diese Kategorie fallen unter anderem Stilattribute bezüglich Farbe, Ausrichtung, Dekoration und Abständen.
Farbe
Das Attribut, um die Farbe des Textes in einem HTML-Element zu ändern, heißt color.
Was insbesondere gern durcheinandergebracht wird: das Attribut, um die Farbe des HTML-Elements selbst zu verändern, ist nicht color (das wäre die Textfarbe), sondern background-color.
Farben können entweder mit ihren Namen (z. B. dark-blue, hot-pink oder gainsboro) oder mit RGB(A)-Codes bezeichnet werden, wobei die Werte für den roten, grünen, blauen und transparenten (“Alpha”) Farbkanal angegeben werden, wie wir es bereits von der Codierung von Bilddaten kennen.
Die Farbwerte können entweder in dezimaler oder hexadezimaler Notation angegeben werden. In der Dezimalschreibweise notieren wur rgb(R, G, B) bzw. rgba(R, G, B, A), wobei R, G, B Zahlen zwischen 0 und 255 sein müssen (die Rot-, Grün- und Blauwerte) und A (der “Alpha”-Wert bzw. die Deckkraft) als Dezimalzahl zwischen 0 und 1 oder als Prozentangabe angegeben werden kann. In der Hexadezimalschreibweise notieren wir #RRGGBB oder #RRGGBBAA, wobei RR, GG, BB und AA jeweils zwei Hexadezimalziffern sind, die eine Zahl zwischen 0 und 255 beschreiben (z. B. #0080FF für Himmelblau).
Um alle Links in einem leicht durchscheinenden Pink einzufärben, ließe sich folgende CSS-Regel verwenden:
a {
color: rgb(192, 1, 186, 0.75)
}
oder die äquivalente Schreibweise
a {
color: #C001BABE;
}
Ausrichtung
Mit CSS können Texte in einem HTML-Element horizontal und vertikal ausgerichtet werden. Für die horizontale Ausrichtung des Textes in einem HTML-Element wird das Attribut text-align auf left für linksbündigen Text, right für rechtsbündigen Text, center für zentrierten Text oder justify für Blocksatz gesetzt.
Bei der Verwendung von Blocksatz mittels text-align: justify kann zusätzlich eine Methode spezifiziert werden, mit der der Text ausgerichtet wird. Mit text-justify: inter-word wird festgelegt, dass nur die Abstände zwischen den Wörtern angepasst werden sollen. Mit der Einstellung text-justify: inter-character werden auch die Abstände zwischen den einzelnen Zeichen verändert.
Die erste Zeile eines Absatzes kann mit dem Attribut text-indent eingerückt werden. Als Parameter kann entweder eine feste Länge oder eine relative Breite in Prozent angegeben werden.
Die letzte Zeile eines in Blocksatz gesetzten Textes erscheint üblicherweise linksbündig. Dies lässt sich aber mit dem CSS-Attribut text-align-last anpassen, das dieselben Werte wie text-align annehmen kann.
Die vertikale Ausrichtung ist kompliziert, weswegen an dieser Stelle ausdrücklich nicht alle Möglichkeiten erörtert werden, die CSS bietet. Es gibt ein CSS-Attribut vertical-align, das sich aber in unterschiedlichen Kontexten unterschiedlich verhält.
In Tabellenzellen kann vertical-align u. a. die Werte top, middle und bottom annehmen, um die Inhalte der Tabellenzelle an ihrem oberen oder unteren Rand bzw. in ihrer Mitte auszurichten.
Möchten Sie beispielsweise ein Icon im Kontext einer Textzeile ausrichten, gibt es diverse Möglichkeiten, die in der Abbildung unten aufgezählt sind. Hierbei muss berücksichtigt werden, woran genau sich CSS ausrichtet. Zu jeder Textzeile sind mehrere Hilfslinien definiert, die in der folgenden Abbildung dargestellt sind:
Rot dargestellt sind hier die Basislinien für normalen, hoch- und tiefgestellten Text. Die Objekte [1], [2] und [3] in der Abbildung sind an den Basislinien ausgerichtet. Die entsprechenden CSS-Regeln sind vertical-align: baseline [1], vertical-align: super [2] und vertical-align: sub [3]. Das Objekt wird selbst mit seiner eigenen Basislinie am umgebenden Text ausgerichtet.
Die Objekte [4] und [5] sind an der Schrifthöhe ausgerichtet, also dem Abstand zwischen dem höchsten Punkt des höchsten Zeichens und dem tiefsten Punkt des tiefsten Zeichens. Die Linien für die Schrifthöhe sind blau eingezeichnet. Objekt [4] ist mit der Regel vertical-align: top am oberen Rand der Schrifthöhe ausgerichtet, Objekt [5] mit vertical-align: bottom am unteren Rand. Das Objekt [4] wird dabei mit seiner eigenen Oberkante an der Oberkante des umgebenden Texts ausgerichtet, das Objekt 5 mit seiner eigenen Unterkante an der Unterkante des umgebenden Texts.
Das Objekt [6] ist mit der Regel vertical-align: middle mittig am umgebenden Text ausgerichtet. Genauer wird der Mittelpunkt der Höhe des Objekts ausgerichtet an dem violett markierten Mittelpunkt zwischen der rot markierten Basislinie und der ebenfalls violett markierten Höhe der Kleinbuchstaben des umgebenden Texts.
Mit den Regeln vertical-align: <feste Länge> und vertical-align: <Prozentangabe> kann die Basislinie des Objekts relativ zur Basislinie des umgebenden Textes um eine angegebene Höhe verschoben werden (Objekt [7]). 100 % entsprechen dabei der Zeilenhöhe, die in der Abbildung grün markiert ist. Zu den Größenangaben siehe auch die Referenz zu Größenangaben.
Ein Inhalt soll vertikal in einem Objekt zentriert sein, aber die Größe des Objekts ist irrelevant? Dafür kann einfach das padding-Attribut benutzt werden. Mehr dazu im Abschnitt Rahmen.
Dekoration
Über-, Durch- und Unterstreichungen können mit dem Attribut text-decoration gestaltet werden. Hierzu können Parameter für die Position (overline für Überstreichung, line-through für Durchstreichung oder underline für Unterstreichung), Linienfarbe (siehe Referenz zu Farbwerten), -stil (solid für durchgezogen, dashed für gestrichelt, dotted für gepunktet, wavy für Wellenline oder double für doppelte Linie) und -breite (siehe Referenz zu Größenangaben) angegeben werden.
/* Überschriften werden mit einer 5px breiten doppelten Linie unterstrichen. */
h1 {
text-decoration: underline double 5px;
}
/* Errata werden mit einer roten Schlangenline durchgestrichen. */
.erratum {
text-decoration: line-through red wavy;
}
Mit dem Attribut text-shadow können den Texten Schatten hinzugefügt werden. Als Parameter können (in dieser Reihenfolge) der horizontale und vertikale Abstand des Schattens zum Text, die Schärfe des Schattens sowie dessen Farbe angegeben werden.
/* Ein leicht versetzter scharf konturierter grauer Schatten */
h1 {
text-shadow: 3px 3px 0px gray;
}
/* Ein rotes Glühen direkt hinter dem Text */
h2 {
text-shadow: 0px 0px 10px red;
}
/* CSS, das die Leute zu ihren Lesebrillen greifen lässt */
h3 {
color: #00000000;
text-shadow: 0px 0px 2px black;
}
Abstände
Die Zeilenhöhe, die u. a. für die vertikale Ausrichtung von Objekten in Textzeilen relevant ist (siehe Ausrichtung), kann mit dem Attribut line-height festgelegt werden. line-height kann als Parameter eine absolute oder relative Längeneinheit übergeben bekommen.
Empfehlenswert ist es, eine relative Angabe in Form einer Zahl ohne Maßeinheit anzugeben, z. B. line-height: 1.5. Angaben in Prozent können unerwartete und unerwünschte Ergebnisse produzieren.
Die Abstände zwischen einzelnen Zeichen und ganzen Wörtern können mit den Attributen letter-spacing und word-spacing definiert werden, die jeweils Größenangaben als Parameter erhalten. Es sind auch negative Größenangaben zulässig, um Zeilen, Wörter und Zeichen enger aneinander rücken zu lassen.
Schrift
In diese Kategorie fallen alle Attribute, die das Aussehen einzelner Zeichen, sprich Buchstaben, Zahlen o.ä. ändern.
Alle nachfolgend beschriebenen Attribute können auf einmal mit dem Attribut font gesetzt werden, etwa
font: italic small-caps bold 12px/30px Georgia, serif;
Die Reihenfolge der Parameter ist hier:
font: font-style font-variant font-weight font-size/line-height font-family;
Die genaue Verwendung dieser Parameter werden in den folgenden Abschnitten einzeln erläutert.
Schriftart
Auf verschiedenen Computern sind verschiedene Schriftarten verfügbar, je nachdem, welches Betriebssystem und welche Software dort installiert sind. Wer Microsoft Office benutzt, kann zum Beispiel u. a. auf die Schriftarten Calibri, Candara und Constantia zugreifen, auf Mac-Geräten stehen Avenir Roman und Trattatello zur Verfügung. Bei der Gestaltung von Webseiten sollte dies berücksichtigt werden, damit die Seite für alle wie gewollt aussieht, auch wenn unterschiedliche Betriebssysteme verwendet werden.
Aus diesem Grund akzeptiert das CSS-Attribut font-family nicht nur eine Schriftart als Parameter, sondern gestattet es auch, mehrere anzugeben. Beispielsweise sind für diesen Text folgende Schriftarten vorgesehen:
body {
font-family: -apple-system, system-ui, "Segoe UI", Roboto, Oxygen-Sans, Ubuntu, Cantarell, "Helvetica Neue", sans-serif;
}
Diese Regel wird von links nach rechts ausgewertet, wobei die erste verfügbare Schriftart ausgewählt wird. Einige dieser Einträge stehen für konkrete Schriftarten: "Segoe UI", Roboto, Oxygen-Sans, Ubuntu, Cantarell und "Helvetica Neue". Zu beachten ist hier, dass Namen, die Leerzeichen enthalten, in Anführungszeichen gesetzt werden müssen.
Andere Einträge stehen für Schriftfamilien. Zum Beispiel bedeutet system-ui, dass die Standard-Schriftart des Betriebssystems verwendet werden soll, auf dem die Seite geöffnet wird. Einige ältere Versionen des Safari-Browsers verwenden stattdessen -apple-system.
Der letzte Eintrag (hier: sans-serif) wird als fallback (engl. für “Rückfallebene”) bezeichnet. Er legt fest, dass irgendeine serifenlose Schriftart verwendet werden soll – egal ob Arial, Calibri oder Liberation Sans – falls keine der vorher erwähnten Schriftarten verfügbar ist. Ein solcher Fallback-Eintrag sollte auf jeden Fall einsetzt werden, da er wenigstens ein Mindestmaß an Kontrolle über die Gestaltung der Schriftart gewährleistet. Mögliche Fallback-Parameter sind sans-serif (eine Schriftart ähnlich z. B. Arial), serif (ähnlich z. B. Times New Roman), monospace (für Schriftarten, in denen alle Zeichen gleich breit sind, wie z. B. Courier*_), cursive (für Schreibschrift) und fantasy (für dekorative und verspielte Schriftarten).
Nicht verwechseln: font-family: cursive bedeutet nicht, dass die Schrift kursiv gesetzt wird. Dazu muss font-style: italic angegeben werden.
Schriftgröße
Mit dem Attribut font-size kann die Schriftgröße von Anzeigeelementen festgelegt werden. Als Größenangabe können folgende Werte eingesetzt werden:
- eins der absoluten Schlüsselwörter
xx-small,x-small,small,medium,large,x-largeundxx-large– die genaue Gestaltung bleibt dann dem Browser überlassen - eins der relativen Schlüsselwörter
largerodersmaller– also größer oder kleiner als der Text der umliegenden HTML-Elemente. - eine absolute Größenangabe in
mm,pt,in(ch) oderpx. Bevorzugt solltenpxverwendet werden, da alle anderen Einheiten der Interpretation des einzelnen Browsers unterliegen - eine relative Größenangabe in
%,em,exoderrem. Hierbei beziehen sich%,emundexauf die Schriftgröße des umschließenden HTML-Elements,remauf die Schriftgröße des HTML-Bodys.1ementspricht dabei der normalen Schriftgröße,1exder Höhe der Kleinbuchstaben.
Schriftstil
Um Texte durch Fettdruck oder Kursivdruck hervorzuheben, können die Attribute font-style und font-weight benutzt werden.
font-style kann die Werte normal, italic für kursive Schrift und oblique für schräge Schrift annehmen. In vielen Schriftarten sehen kursive und schräge Schrift identisch aus. Der Unterschied ist, dass für Schrägschrift einfach die normalen, aufrechten Zeichen etwas geneigt werden, während in einigen Schriften für Kursivschrift eigene Zeichen verwendet werden. Die folgende Abbildung demonstriert den Unterschied:
Für Fett- oder Leichtdruck kann das Attribut font-weight verwendet werden. Als Parameter können entweder die festen Werte normal, bold (fett), lighter (leichter als der umgebende Text) und bolder (fetter als der umgebende Text) verwendet werden. Präziser kann der Wert mit einer Zahlenangabe zwischen 1 und 1000 spezifiziert werden, wobei ältere Browser nur die Werte 100, 200, 300, 400 (entspricht der Angabe normal) 500, 600, 700 (entspricht der Angabe bold), 800 und 900 unterstützen und alle anderen Angaben gerundet werden. Für relative Angaben, also lighter und bolder werden nur die Gewichte 100, 400, 700 und 900 berücksichtigt.

Noch ausgefallenere Textgestaltung erlaubt das Attribut font-variant, mit dem unter anderem die Verwendung von besonderen Schriftschnitten für Kapitälchen und Großbuchstaben definiert werden kann.1
Dieses Attribut ist allerdings nicht mit allen Schriftarten kompatibel und sollte daher vorsichtig eingesetzt werden. Einige Werte, die font-variant annehmen kann, sind:
small-capsoderpetite-capsfür Kapitälchen, wobei die Großbuchstaben ihre originale Höhe behaltenall-small-capsoderall-petite-capsfür Kapitälchen, wobei auch die Großbuchstaben verkleinert werdenunicase, wobei nur die Großbuchstaben durch Kapitälchen ersetzt werden und die Kleinbuchstaben ihre Größe behalten2

Referenz
Attribute
| Attribut | Beschreibung | Werte |
|---|---|---|
color |
Textfarbe | Farbwert |
background-color |
Hintergrundfarbe | Farbwert |
font-family |
Schriftart | Name(n) der Schriftart, z. B. Arial, Liberation Sans, sans-serif3 |
font-size |
Schriftgröße | Größenangabe |
font-style |
Schriftstil | normal, italic (kursiv) |
font-weight |
Schriftdicke | normal, bold (fett), Zahlenwert zwischen 1 und 1000 (normal entspricht 400, fett 700) |
text-align |
Horizontale Textausrichtung | left, right, center, justify (Blocksatz) |
vertical-align |
Vertikale Textausrichtung | top, bottom, middle |
border-color |
Farbe des Rahmens | Farbwert |
border-style |
Linienstil des Rahmens | z. B. solid (einfache Linie), double (doppelte Linie), dotted (gepunktet), dashed (gestrichelt), none |
border-width |
Breite des Rahmens | Größenangabe |
margin |
Außenabstand zu allen Seiten | Größenangabe |
margin-top/-bottom/-left/-right |
Außenabstand oben, unten, links, rechts | Größenangabe |
padding |
Innenabstand zu allen Seiten | Größenangabe |
padding-top/-bottom/-left/-right |
Innenabstand oben, unten, links, rechts | Größenangabe |
width, height |
Breite, Höhe | Größenangabe |
list-style-type |
Aufzählungsstil oder -symbol für Listenelemente | circle (Kreis), disc (gefüllter Kreis), square (gefülltes Quadrat), decimal (nummeriert), lower-/upper-roman (römische Ziffern), none, Zeichenkette (z. B. "* ") |
Rahmenstile lassen sich auch in Kurzform mit dem Stilattribut border festlegen, das drei Argumente erwartet: Breite, Linienstil und Farbe (z. B.: border: 1px solid black;). Bei allen Rahmen-Stilattributen kann border auch durch border-top, border-left usw. ersetzt werden, um einen Rahmenstil für eine bestimmte Seite festzulegen.
Farbwerte
Farbwerte lassen sich in CSS als dezimale RGB-Werte oder RGB-Werte im Hexadezimalformat angeben (jeweils mit 8 Bit pro Farbkanal). Häufig verwendete Farbwerte sind auch durch einen Namen spezifiziert, der alternativ angegeben werden kann (siehe Farbreferenz bei W3Schools):
- Farbname, z. B.:
red,gray,yellow - RGB-Werte (dezimal), z. B.:
rgb(255, 0, 0),rgb(128, 128, 128),rgb(255, 255, 0) - RGB-Werte (hexadezimal), z. B.:
#ff0000,#808080,#ffff00
Größenangaben
Größenangaben (z. B. Schriftgrößen, Höhe und Breite von Elementen, Linienbreiten, Abstände) lassen sich in Pixeln, in absoluten Maßeinheiten oder als relative Größen bzgl. der Größe oder Schriftgröße des Elternelements angeben:
- Wert in Pixeln, z. B.:
1px,50px - Absoluter Wert in cm/mm,4 z. B.:
1cm,1000mm - Wert relativ zur Größe des Elternelements, z. B.:
50%(halb so groß wie das Elternelement) - Wert relativ zur Schriftgröße des Elternelements, z. B.:
0.5em(halb so groß wie die Schriftgröße des Elternelements) - Wert relativ zur Schriftgröße des
<html>-Elements, z. B.:2rem(doppelt so groß wie die Schriftgröße des<html>-Elements)
Wird bei einer Größenangabe ein numerischer Wert ohne Einheit verwendet, wird dieser in der Regel als Wert in Pixeln interpretiert.
Zum Gestalten von Webseiten, die am Bildschirm betrachtet werden, sollten möglichst keine absolute Maßeinheiten wie cm verwendet werden, da Bildschirmgrößen stark variieren können und unterschiedlich große Bildschirme meist nicht von der gleichen Entfernung aus betrachtet werden. Stattdessen sollten hier möglichst nur die Einheiten px oder em/rem verwendet werden, die auf der Einheit Pixel basieren.
Validierung
Für CSS-Daten gilt wie für HTML (und formale Sprachen im Allgemeinen), dass sie nur dann valide sind, wenn sie die oben beschriebenen formalen Regeln einhalten, die in den CSS-Standards des W3C genauer spezifiziert sind.5
Um CSS-Dokumente auf Fehler zu überprüfen, können CSS-Validatoren verwendet werden, die auf ähnliche Weise wie HTML-Validatoren funktionieren, indem sie das Dokument auf die Einhaltung der aktuellen CSS-Standards überprüfen.
Tool: Um zu überprüfen, ob ein CSS-Dokument valide ist, kann der Online-Validator des W3C verwendet werden: https://jigsaw.w3.org/css-validator
Weiterführende Links
- CSS-Referenz von W3Schools: https://www.w3schools.com/CSS/
- Vollständige CSS-Referenz des Mozilla Developer Network: https://developer.mozilla.org/de/docs/Web/CSS/Reference
-
font-variantist ein sehr umfangreiches Attribut, an dessen Oberfläche hier nur gekratzt wird. Eine vollständige Dokumentation findet sich auf den Seiten des Mozilla Developer Network: font-variant ↩︎ -
Falls der Text wie auf dem Cover von Frank Schätzings “Der Schwarm” aussehen soll. ↩︎
-
Werden mehrere Schriftarten durch Komma getrennt angegeben, wird die erste Schriftart zur Darstellung gewählt, die auf dem System vorhanden ist.
Wird einer der folgenden generischen Schriftartbezeichner angegeben, wählt der Browser selbst eine geeignete vorhandene Schriftart zur Darstellung aus:sans-serif(serifenlose Schrift),serif(Serifenschrift),monospace(Festbreitenschrift),cursive(Schreibschrift). ↩︎ -
Daneben gibt es weitere absolute Maßeinheiten, die aus dem internationalen Gebrauch (in für Inch), oder der Typographie (pc für Pica, pt für Point) bekannt sind. Das Umrechnungsverhältnis zwischen diesen Maßeinheitn ist definiert als: 1 in = 2.54 cm = 25.4 mm = 6 pc = 72 pt ↩︎
-
siehe offizielle Homepage des W3C zu CSS: https://www.w3.org/Style/CSS ↩︎
3. Algorithmik
3.1 Einstieg in die Algorithmik
Das Online-Skript zum Thema “Algorithmik” befindet sich zur Zeit noch im Aufbau.
Einleitung
Algorithmen – also abstrakte Beschreibungen von Programmen oder allgemeiner: Lösungsverfahren für bestimmte Aufgabenstellungen – sind uns bereits in mehreren Zusammenhängen begegnet: In der visuellen Programmierung haben wir selbst Algorithmen entwickelt und in der Programmiersprache Scratch umgesetzt, etwa um eine Spielfigur zu steuern oder ein Quiz zu entwickeln, im Kapitel “Informationsdarstellung” wurden Algorithmen zum Berechnen von Prüfziffern für Barcodes oder zur Datenkompression behandelt.
In diesem Kapitel werden wir Algorithmen unter abstrakteren Gesichtspunkten betrachten, also welche Eigenschaften Algorithmen haben, welche grundlegenden Strategien sich in Algorithmen finden lassen, und wie sich Algorithmen unabhängig von einer konkreten Programmiersprache formulieren lassen.
Dieser allgemeinere Blick ist sinnvoll, da die Bildungsziele, die mit den Themen “Programmierkompetenz” und “Algorithmik” verknüpft sind, weniger auf rein technisches Verständnis abzielen, also etwa das Beherrschen einzelner Programmiersprachen, sondern auf die Förderung des sogenannten “algorithmischen Denkens” (Computational Thinking) als Metakompetenz.
So heißt es in den Fachanforderungen in der Einleitung zum inhaltsbezogenen Kompetenzbereich “Algorithmen und Programmierung”:
Indem die Schülerinnen und Schüler Handlungsabläufe in natürlicher Sprache strukturiert darstellen, erlernen sie mit Kontrollstrukturen die Grundelemente imperativer Programme sowie des algorithmischen Denkens (Computational Thinking).
Computational Thinking
Der Begriff “Computation Thinking”1 (oft als “Informatisches Denken” oder “Algorithmisches Denken” übersetzt) bezeichnet kurz zusammengefasst eine Kompetenz zum (meist maschinellen) Lösen komplexer Probleme. Es beschreibt einen gedanklichen Prozess zur Lösungsplanung, der darauf basiert, Problemstellungen und ihre Lösungen so darzustellen, dass die Problemlösungen auch durch eine Maschine, z. B. einen Computer, durchgeführt werden können. Dazu wird der Lösungsprozess in immer kleinere Teilschritte zerlegt, bis nur noch maschinell durchführbare Grundstrukturen übrigbleiben – also etwa elementare Rechenoperationen bzw. Anweisungen, Sequenzen, Wiederholungen und Fallunterscheidungen.
Computational Thinking wird manchmal fälschlicherweise mit dem Programmieren gleichgesetzt, geht aber als Denkmodell zum Lösen komplexer Probleme darüber hinaus und gilt heute weitestgehend übereinstimmend als Schlüsselkompetenz. Auf der anderen Seite ist aber auch klar, dass Programmierenlernen und der Kompentenzerwerb des “Computational Thinking” intrinsisch miteinander verwoben sind – das Erlernen einer Programmiersprache stellt einen wichtigen Zugang zum “Computational Thinking” dar, während andersherum der strukturierte Problemlöseprozess des “Computational Thinking” eine wesentliche Voraussetzung zum erfolgreichen Entwickeln von Programmen ist.
Was ist ein Algorithmus?
Der Begriff “Algorithmus” lässt sich folgendermaßen definieren:
Ein Algorithmus ist eine eindeutige Handlungsvorschrift zur Lösung eines Problems, die aus endlich vielen wohldefinierten Einzelschritten besteht. Dabei wird beschrieben, wie eine Eingabe Schritt für Schritt in eine Ausgabe überführt wird.
Die Eingabedaten beschreiben dabei das gegebene Problem und werden durch den Algorithmus verarbeitet, dessen Ausgabedaten die Lösung beschreiben. Die Verarbeitungsvorschrift – also der Algorithmus – muss dabei so präzise und eindeutig formuliert sein, dass selbst eine Maschine (z. B. ein Computer) sie durch stures Befolgen der Befehle durchführen kann.

Alltagsbeispiele, die oft als Analogien für Algorithmen verwendet werden, sind etwa Kochrezepte oder Spielanleitungen.2
Ein Algorithmus lässt sich quasi als abstrakte Form eines Programms auffassen. Programme wiederum setzen Algorithmen in einer konkreten Programmiersprache um, sie implementieren die Algorithmen.
Eigenschaften von Algorithmen
Damit eine Handlungsvorschrift als Algorithmus gilt, muss sie mehrere grundlegende Eigenschaften erfüllen, die sicherstellen, dass auch eine rein maschinelle Ausführung möglich ist:
-
Allgemeinheit: Das Lösungsverfahren muss eine ganze Klasse von Problemen lösen und nicht nur eine spezielle Probleminstanz.
Eine Handlungsanweisung, die angibt, wie die Wurzel der Zahl 81 berechnet wird, wäre nicht allgemein (hier würde es prinzipiell reichen, einfach den Wert 9 zurückzugeben), während eine Anleitung, wie die Wurzel einer beliebigen positiven Zahl berechnet wird, als allgemein gelten würde. -
Ausführbarkeit: Jeder Einzelschritt und jede einzelne Anweisung, die im Algorithmus vorkommt, muss ausführbar sein. Dazu muss jede Anweisung insbesondere so formuliert sein, dass klar ist, wie sie durchgeführt werden muss. Ist eine Anweisung dagegen zu komplex, muss sie gegebenenfalls durch einen Unteralgorithmus in Form von weiteren Einzelschritten präzisiert werden.
Hierbei spielt die Frage eine Rolle, was als “elementare Anweisung” gilt. Dazu muss berücksichtigt werden, durch wen und in welchem Kontext der Algorithmus ausgeführt wird, und was mit den hierbei verwendeten Objekten gemacht werden kann: Bei einem Computerprogramm ist die Menge der ausführbaren Anweisungen durch die verwendete Programmiersprache und die Methoden der Datenstrukturen beschränkt. Wenn wir unserem Hund (oder vielleicht auch einem Roboterhund) Kunststücke beibringen möchten, müssen wir uns auf die Befehle beschränken, die er versteht. -
Endlichkeit: Die Beschreibung der Handlungsvorschrift muss eine endliche Länge besitzen, also mit endlich vielen Anweisungen auskommen, beispielsweise als Text auf einer Seite. Diese Eigenschaft wird auch als Finitheit oder auch spezifischer als “statische Endlichkeit” bezeichnet, um zu betonen, dass hier die Begrenztheit der Beschreibung des Algorithmus gemeint ist und nicht seiner Ausführungsdauer.
-
Eindeutigkeit: Die Abfolge der einzelnen Schritte in der Handlungsvorschrift muss genau festgelegt sein. Zu jedem Zeitpunkt der Ausführung muss also klar sein, welcher Schritt als Nächstes ausgeführt wird. Das bedeutet nicht, dass es nur eine einzige Reihenfolge gibt, in der die Einzelschritte eines Algorithmus durchlaufen werden: Durch bedingte Wiederholungen und Fallunterscheidungen sind je nach Eingabe unterschiedliche Abfolgen möglich. Dabei muss aber klar festgelegt sein, wann und unter welcher Bedingung welcher Weg gewählt wird.
Verfahren, die zufallsbasiert Entscheidungen fällen, zählen aber auch als Algorithmen. Der Begriff der “Eindeutigkeit” wird in der theoretischen Informatik daher noch weiter differenziert in Determinismus und Determiniertheit.
-
Determinismus: Ein Algorithmus gilt als deterministisch, wenn er bei wiederholter Ausführung mit der gleichen Eingabe immer den gleichen Ablauf hat – also dieselben Einzelschritte in derselben Reihenfolge durchläuft.
-
Determiniertheit: Der Begriff der Determiniertheit ist weniger streng als Determinismus: Ein Algorithmus gilt als determiniert, wenn er bei wiederholter Ausführung mit der gleichen Eingabe immer das gleiche Ergebnis liefert, aber nicht unbedingt immer auf demselben Weg. Das kann etwa der Fall sein, wenn bestimmte Entscheidungen im Algorithmus zufallsbasiert getroffen werden, aber trotzdem sichergestellt ist, dass der Algorithmus immer die richtige (und damit gleiche) Lösung berechnet.3
- Korrektheit: Nicht zuletzt muss das Lösungsverfahren für jede Eingabe die richtige Lösung liefern. Die Korrektheit eines Algorithmus kann exemplarisch anhand von repräsentativen Testfällen gezeigt werden oder mit formalen Methode theoretisch bewiesen werden. Formale Beweise für Algorithmen sind eines der wichtigsten Themengebiete der Theoretischen Informatik, setzen aber höhere mathematische Kenntnisse voraus.
Prozessbezogene Eigenschaften
Ein Algorithmus lässt sich neben seiner Beschreibung auch auf Aspekte untersuchen, die sich auf seinen Ausführungsprozess beziehen.
-
Terminiertheit: Ein Algorithmus sollte für jede Eingabe nach einer endlichen Rechenzeit zu einer Lösung kommen – er muss also nach endlich vielen Einzelschritten terminieren. Anderenfalls hätte der Algorithmus keinen praktischen Nutzen.
-
Dynamische Endlichkeit: Der Speicherplatz, der während der Ausführung für Variablen und Datenstrukturen benötigt wird, muss ebenfalls endlich sein. In der Praxis muss der Speicherbedarf darüber hinaus in einem angemessenen Rahmen bleiben in Bezug auf das System, auf dem der Algorithmus als Programm ausgeführt werden soll (z. B. auf einem Handy, PC oder einem Hochleistungsrechner).
-
Komplexität: Der theoretische Aufwand an Rechenzeit und Speicherbedarf eines Algorithmus wird unter dem Begriff “Komplexität” zusammengefasst.
-
Effizienz: Ein Algorithmus gilt als effizient, wenn seine Komplexität – also Rechenzeit und Speicherbedarf in Abhängigkeit von der Größe des Problems – “gut” ist, also so niedrig wie nötig oder möglich für die Problemklasse, die er löst.
Beschreibung von Algorithmen
Wir wissen bereits aus den vorigen Lektionen (z. B. aus der Einführung in die visuelle Programmierung), dass sich Algorithmen mit Hilfe von bestimmten Grundbausteinen konstruieren lassen, nämlich aus:
- einzelnen Anweisungen
- Sequenzen von Grundbausteinen
- Kontrollstrukturen
Die sogenannten Kontrollstrukturen sind spezielle Anweisungen zur Ablaufsteuerung weiterer Grundbausteine. Dazu gehören im Wesentlichen:
- Wiederholungen
- Fallunterscheidungen
Bei Wiederholungen werden bestimmte Grundbausteine mehrmals nacheinander ausgeführt, wobei es in der Regel von bestimmten angegebenen Bedingungen abhängt, wie viele Wiederholungsschritte durchgeführt werden. Bei Fallunterscheidungen (bzw. bedingten Anweisungen) werden bestimmte Grundbausteine in Abhängigkeit von bestimmten Bedingungen ausgeführt oder nicht. Daneben kommen als weitere Bestandteile von Algorithmen Ausdrücke vor, zum Beispiel mathematische Ausdrücke oder Vergleiche, die unter anderem zur Berechnung von Parameterwerten für Anweisungen, Werten für Variablen oder als Bedingungen der Kontrollstrukturen dienen.
Welche Anweisungen konkret ausführbar sind, hängt dabei wie oben erwähnt vom Kontext ab (in der Programmierung z. B. von der verwendeten Programmiersprache). Variablenzuweisungen – also das Speichern eines Wertes, der durch einen Ausdruck berechnet wird, in einer Variablen – sind Anweisungen, die in der imperativen Programmierung in der Regel immer zur Verfügung stehen. In der objektbasierten Programmierung (z. B. in Scratch) gibt es daneben größtenteils Anweisungen, um den Zustand von Objekten zu ändern, sowie Ausdrücke, um ihren Zustand abzufragen (z. B. Position einer Figur auf der Zeichenfläche abfragen oder eine Figur auf der Zeichenfläche um 10 Pixel verschieben).
Beispiel: Code knacken
Als praktisches Beispiel für den Entwurf und die Analyse von Algorithmen soll das folgende Problem betrachtet werden: Angenommen, Sie haben Ihr Fahrrad mit einem Zahlenschloss gesichert, in dem vier Stellen auf die Ziffern 0 bis 9 gedreht werden können. Leider haben Sie die richtige Zahlenkombination vergessen. Es soll nun ein Algorithmus entwickelt werden, der beschreibt, wie sich durch systematisches Überprüfen aller Kombinationen von 0000 bis 9999 die richtige Kombination ermitteln lässt.
Dabei lassen sich die folgenden Aktionen durchführen: Die einzelnen Ziffern können durch Vor- und Zurückdrehen der einzelnen Räder eingestellt werden, und es kann durch Ziehen am Bügel geprüft werden, ob das Schloss für die gerade eingestellte Zahl offen ist.
Tool: In dieser interaktiven Anzeige können Sie Ihren Algorithmus testen.4 Klicken Sie die Schaltfläche an, um zu versuchen, das Schloss zu öffnen. Die Schaltfläche setzt das Schloss auf eine zufällige Kombination zurück und legt eine neue Kombination als Lösung fest. Mit den Schaltflächen und können Sie die Anzahl der Stellen verringern (um das Problem zu vereinfachen) oder erhöhen.
Dabei sollten Sie maximal für zwei Stellen versuchen, manuell die richtige Lösung zu finden, da das Ermitteln der richtigen Kombination sehr langwierig werden kann – bei 4 Stellen müssen immerhin 10000 verschiedene Kombinationen ausgetestet werden. Solche Aufgaben sind also eher für Maschinen geeignet, weswegen der Algorithmus möglichst präzise und eindeutig formuliert werden sollte.
Wir untersuchen als Nächstes verschiedene Vorschläge, wie ein Lösungsverfahren formuliert werden könnte, und überprüfen daran jeweils die grundlegenden Eigenschaften von Algorithmen.
1. Ansatz
Der erste Vorschlag, ein Lösungsverfahren zu beschreiben, besteht aus einem einzigen Satz:
- Teste nacheinander jede Kombination der Ziffern
0bis9.
Diese Beschreibung ist allgemein, da sie unabhängig davon funktioniert, welches Ergebnis das richtige ist – wenn dagegen nur vorgeschlagen würde “Teste die Zahl 8361” kann das für ein bestimmtes Zahlenschloss die richtige Lösung liefern, im Allgemeinfall aber nicht. Die Beschreibung ist natürlich auch endlich, da sie in einem Satz formuliert wird.
Sie ist allerdings weder ausführbar noch eindeutig: Für Menschen ist die Anleitung aus dem Kontext heraus zwar verständlich, für eine Maschine ist aber im Detail unklar, wie die Einzelschritte ausgeführt werden sollen. Darüber hinaus ist die Reihenfolge der Einzelschritte unklar.

2. Ansatz
Um das Lösungsverfahren möglichst eindeutig und ausführbar zu beschreiben, sollten wir uns also auf einfache, elementare Anweisungen beschränken, die darüber hinaus so formuliert sind, dass klar wird, in welcher Reihenfolge, in Abhängigkeit von welchen Bedingungen und wie oft die Einzelschritte ausgeführt werden sollen:
- Stelle Code
0000ein - Versuche Schloss zu öffnen
- Wiederhole bis Schloss offen ist:
- Stelle nächsten Code ein
- Versuche Schloss zu öffnen
Diese Anleitung erfüllt die Mindestanforderungen an einen Algorithmus: Sie ist endlich, allgemein, eindeutig und ausführbar, sofern die enthaltenen Anweisungen “stelle Code 0000 ein”, “stelle nächsten Code ein” für das ausführende System verständlich genug sind – anderenfalls müssten wir diese Anweisungen präzisieren, indem wir uns auf elementarste Anweisungen beschränken, was wir im nächsten Abschnitt noch vertiefen werden.

3. Ansatz
Der nächste Vorschlag beinhaltet zufallsbasierte Entscheidungen:
- Wiederhole bis Schloss offen ist:
- Stelle zufälligen Code ein
- Versuche Schloss zu öffnen
Auch diese Beschreibung stellt einen Algorithmus dar, sofern die Anweisung “stelle zufälligen Code ein” als ausführbar gilt. Hier wird also ein Zufallszahlengenerator benötigt. Außerdem ist die Anzahl der Wiederholungen hier nicht in jedem Ablauf für dieselbe Eingabe (das heißt hier: für dasselbe Schloss) gleich, der Algorithmus ist also nicht deterministisch. Auf der anderen Seite ist zu jedem Zeitpunkt klar, welche Anweisung als nächste ausgeführt wird, der Algorithmus ist also trotzdem eindeutig.
Diese Beschreibung stellt also ein typisches Beispiel für einen randomisierten Algorithmus dar, also einen Algorithmus, in dem einzelne Entscheidungen zufallsbasiert getroffen werden.3 Theoretisch kann es passieren, dass dieser Algorithmus nie terminiert (wenn zufälligerweise die richtige Zahlenkombination niemals gewählt wird), was aber extrem unwahrscheinlich ist. Wir können davon ausgehen, dass der Algorithmus in endlicher Zeit die richtige Lösung liefert, er ist also determiniert.

4. Ansatz
Betrachten wir noch einen weiteren Ansatz zum Einstellen der richtigen Ziffern:
- Wiederhole für 1. bis 4. Stelle:
- Wiederhole bis Ziffer an dieser Stelle richtig ist:
- Stelle nächste Ziffer ein
- Wiederhole bis Ziffer an dieser Stelle richtig ist:
- Öffne Schloss
Dieses Verfahren ist zwar allgemein, endlich und eindeutig formuliert, für die gegebene Problemstellung aber nicht ausführbar, da die Überprüfung, ob eine Ziffer an einer bestimmten Stelle richtig ist, nicht möglich ist. Wir können nur überprüfen, ob die gesamte eingestellte Zahlenkombination richtig ist, indem wir versuchen, das Schloss zu öffnen.
Auf den Kontext objektbasierter Programmierung übertragen bedeutet das, dass wir hier Methoden von Objekten benötigen würden, die von diesen nicht unterstützt werden.

Zwischenfazit
Ein Algorithmus sollte so einfach wie möglich, aber so genau wie nötig formuliert werden. Hier finden Sie Hinweise, wie dazu am besten vorgegangen werden sollte.
- Zuerst sollte überlegt werden, welche elementaren Anweisungen und Werteabfragen verwendet werden dürfen, um das Problem zu lösen. Das hängt natürlich stark vom gegebenen Problemkontext ab.
- Diese elementaren Anweisungen werden dann mit den grundlegenden Kontrollstrukturen (“wiederhole solange/bis …”, “falls … mache … sonst …”) kombiniert, um eine eindeutige Abfolge von Einzelschritten zu formulieren.
- Daneben dürfen in der Regel immer auch eigene Variablen zur Problemlösung verwendet werden.5 Variablenzuweisungen sind also Anweisungen, die wir unabhängig vom konkreten Problemkontext immer verwenden dürfen.
- Außerdem dürfen immer logische Ausdrücke (z. B. Vergleich, Verknüpfung von Vergleich mit “und”, “oder”) und mathematische Ausdrücke (z. B. Addition, Multiplikation, Funktionsaufrufe) zur Berechnung von Parameterwerten, Variablenwerten oder Bedingungen verwendet werden. Solche Ausdrücke können als allgemein bekannt gelten oder vereinbart werden.
Komplexere Anweisungen können in Form von Unteralgorithmen formuliert werden, ggf. auch mit Parametern (vgl. Unterprogramme in Scratch). Das macht besonders dann Sinn, wenn solche komplexeren Anweisungen an mehreren Stellen im Algorithmus verwendet werden.
Auf diese Weise erhalten wir klar verständliche, wenn auch sprachlich nicht ganz natürlich formulierte Handlungsanweisungen. Diese stark reduzierte und formalisierte Sprache wird als Pseudocode bezeichnet, da sie schon relativ nahe am Code einer Programmiersprache liegt.
Vertiefung: Code knacken
Wir betrachten hier noch einmal den 2. Ansatz für das Ermitteln der richtige Zahlenkombination:
- Stelle Code
0000ein - Versuche Schloss zu öffnen
- Wiederhole bis Schloss offen ist:
- Stelle nächsten Code ein
- Versuche Schloss zu öffnen
Um das Verfahren in allen Einzelschritten möglichst klar zu beschreiben, beschränken wir uns nun aber bei den elementaren Anweisungen auf die folgenden:6
Drehe Stelle ... weiter Versuche Schloss zu öffnen
In Bedingungen und anderen Ausdrücken beschränken wir uns bei den Zustandsabfragen für dieses Problem auf die folgenden:7
-
Ziffer an Stelle ... ist eine Ziffer zwischen
0und9. - Zustand des Schlosses ist “offen” oder “geschlossen”.
Zur Angabe der Stellenposition sollte hierbei jeweils eine Zahl zwischen 1 und 4 gewählt werden, z. B. “Drehe Stelle 1 weiter”.
Die Anweisungen “stelle Code 0000 ein” und “stelle nächsten Code ein” gelten unter diesen Voraussetzungen als zu komplex und damit als nicht ausführbar. Daher werden wir diese Anweisungen durch Unteralgorithmen präzisieren.
Unteralgorithmen
Code 0000 einstellen
Formulieren wir als Erstes einen Unteralgorithmus für die Anweisung “stelle Code 0000 ein”, d. h. setze alle Stellen auf 0:
- Wiederhole für 1. bis 4. Stelle:
- Wiederhole solange die aktuelle Stelle ≠
0ist:- Drehe die aktuelle Stelle weiter
- Wiederhole solange die aktuelle Stelle ≠
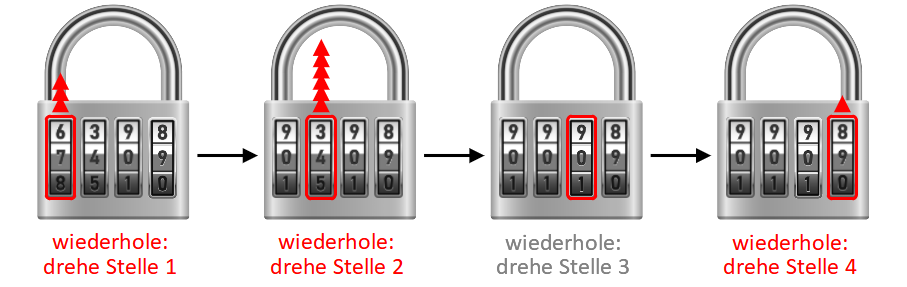
Formulierungen wie “die aktuelle Stelle” können allerdings verwirrend sein und für die maschinelle Ausführung zu unklar. Besser ist es, solche Formulierungen durch Variablen zu präzisieren:
- Setze n auf 1
- Wiederhole 4-mal:
- Wiederhole solange n-te Stelle ≠
0:- Drehe n-te Stelle weiter
- Erhöhe n um 1
- Wiederhole solange n-te Stelle ≠
Hier wird eine Variable n verwendet, um die “aktuelle Stelle” zu kennzeichnen: Wir beginnen bei Stelle 1 und wiederholen für alle Stellen 1 bis 4. Hier ist zu jedem Zeitpunkt klar, was mit der “aktuellen Stelle” gemeint ist.
Nächsten Code einstellen
Sehen wir uns nun an, wie die Anweisung “stelle nächsten Code ein” mit Hilfe elementarer Anweisungen formuliert werden kann: Im Prinzip soll hier nur die letzte Stelle einmal weitergedreht werden. Dabei müssen wir aber Überträge berücksichtigen: Wenn wir die letzte Stelle auf 0 drehen (z. B. von 1899 auf 1890), müssen wir ebenfalls die vorletzte Stelle weiterdrehen (von 1890 auf 1800). Das muss wiederholt werden (1800 auf 1900), bis wir eine Stelle nicht auf 0 gedreht haben, sondern auf eine andere Ziffer.
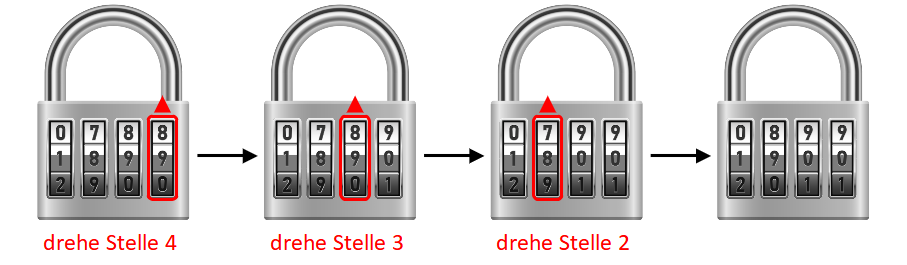
Wir müssen also einen Algorithmus zur “Addition von 1 mit Übertrag” formulieren:
- Setze n auf 4
- Drehe n-te Stelle weiter
- Wiederhole solange n-te Stelle =
0:- Verringere n um 1
- Drehe n-te Stelle weiter
Wir beginnen bei der letzten Stelle, drehen diese einmal weiter, und solange wir beim Weiterdrehen 0 als neuen Wert der Stelle erhalten wiederholen wir diesen Prozess für die jeweils vorige Stelle. Die Wiederholung lässt sich auch äquivalent mit “bis ungleich 0” statt “solange gleich 0” formulieren:
- Wiederhole bis n-te Stelle ≠
0:- …
Der so formulierte Algorithmus mit Unteralgorithmen ist nun bezüglich der festgelegten elementaren Anweisungen und Zustandsabfragen ausführbar und könnte so auch in einer einfachen Programmiersprache umgesetzt werden.

Sie haben sich eventuell schon gefragt, ob es wirklich nötig ist, zu Beginn die Zahlenkombination 0000 einzustellen. Die Antwort lautet: nein. Im Prinzip können wir von jeder beliebigen Zahlenkombination aus starten – nach spätestens 10000 Versuchen müssen wir den richtigen Code gefunden haben. In diesem Fall müssten wir den Unteralgorithmus “stelle nächsten Code ein” aber anpassen, da es dann passieren kann, dass wir von der Zahlenkombination 9999 aus weiterdrehen.
Warum ist dieser Fall problematisch? Es werden alle Stellen von der 4-ten aus jeweils von 9 auf 0 weitergedreht, bis die 1. Stelle erreicht und auf 0 gedreht wird. Laut Algorithmus wird nun n auf 0 gesetzt und die 0-te Stelle weitergedreht, was Unsinn ist. Dieser Sonderfall ist für Menschen klar (an dieser Stelle wird abgebrochen), für eine Maschine aber nicht: Bei der Programmausführung wird hier in der Regel ein Fehler auftreten, da es keine “0-te Stelle” gibt. Wir müssen die Abbruchbedingung im Algorithmus für diesen Sonderfall also explizit anpassen:
- Wiederhole solange n-te Stelle =
0und n > 1:- …
Auf diese Weise wird die Wiederholung auch dann beendet, wenn die 1. Stelle erreicht und weitergedreht worden ist (auch wenn sie dabei ebenfalls auf 0 gedreht wird).8
Algorithmus verallgemeinern
Wir haben so also einen eindeutigen und mit grundlegendsten Anweisungen ausführbaren Algorithmus zum Ermitteln der richtigen Zahlenkombination gefunden, der das Problem allgemein für alle Zahlenschlösser mit 4 Stellen löst – unabhängig davon, was die richtige Kombination ist. Was aber, wenn wir ein Zahlenschloss mit mehr Stellen, ein Schloss mit Buchstabenkombination oder gar ein Schloss mit Farbkombination haben?

Zunächst verallgemeinern wir das Lösungsverfahren weiter, indem wir die Beschränkung auf 4 Stellen aufheben und stattdessen die Anzahl der Stellen als frei wählbaren Eingabeparameter angeben. Nennen wir diesen Wert beispielsweise Anzahl, so muss in den Beschreibungen des Algorithmus und seiner Unteralgorithmen aus diesem Abschnitt jedes Vorkommen des Werts 4 durch den Wert von Anzahl ersetzt werden. Nun lassen sich mit demselben Algorithmen auch Zahlenschlösser mit 3, 5 oder 100 Ziffern knacken, indem einfach der Wert für Anzahl variiert wird.
Ähnlich können wir den Algorithmus so verallgemeinern, dass wir nicht auf die Ziffern 0 bis 9 für die einzelnen Stellen beschränkt sind, sondern beliebige Zeichen für die Kombination verwenden können – etwa die Buchstaben A bis Z, verschiedene Farben oder mysteriöse Symbole. In diesem Fall muss das Zeichen 0 in der Abbruchbedingung des Unteralgorithmus “stelle nächsten Code ein” einfach durch ein beliebiges (z. B. das erste) der verwendeten Zeichen ersetzt werden, das hier mit dem Parameter Startzeichen bezeichnet wird:9
- Wiederhole solange n-te Stelle = Startzeichen und n > 1:
- …
Für ein Buchstabenschloss mit 8 Stellen würden wir den Algorithmus dann mit den konkreten Parameterwerten Anzahl = 8 und Startzeichen = A durchführen (und müssten im schlimmsten Fall 268 ≈ 200 Mrd. verschiedene Kombinationen austesten…).
Auf einer abstrakteren Ebene beschreibt dieser Algorithmus ein sehr einfaches (und im Zweifelsfall sehr aufwendiges) Suchverfahren nach einem Codewort oder Passwort mit einer bestimmten Länge und begrenzten Zeichenmenge, hier durch ein Kombinationsschloss verschaulicht. Dabei werden der Reihe nach alle möglichen Zeichenkombinationen durchgegangen, bis die richtige Kombination gefunden wurde.10
-
siehe auch Peer Stechert: Computational Thinking aus der Reihe Informatikdidaktik kurz gefasst (Teil 8), Video bei YouTube ↩︎
-
Solche Beispiele eignen sich teils aber nur bedingt, da ihre Beschreibungen zwar für einen Menschen verständlich, aber für eine Maschine im Detail meist zu ungenau formuliert werden. ↩︎
-
Tatsächlich können Computerprogramme nicht mit “echtem” Zufall arbeiten: Zufallszahlen werden in Rechnern meist durch zufällig wirkende, aber in Wirklichkeit deterministische Verfahren generiert, die daher auch als Pseudozufallszahlengeneratoren bezeichnet werden. Dabei werden in der Regel unkontrollierbare (also “zufällige”) Faktoren als Eingabe mit einbezogen, z. B. die aktuelle Rechnerzeit beim Starten des Programms. ↩︎ ↩︎
-
Die Grafiken für die Zahlenschlösser stammen von Vecteezy. ↩︎
-
Eventuell bietet es sich in Abhängigkeit von der Zielgruppe und dem Problemkontext aber auch an, Variablen als greifbare Objekte in das Gesamtszenario zu integrieren, z. B. als kleine Notizzettel oder Schieberegler zu umschreiben. ↩︎
-
Kontrollstrukturen und Variablenzuweisungen können aber wie üblich ohne Einschränkung verwendet werden, wenn nötig. ↩︎
-
Daneben können aber wie üblich allgemein bekannte mathematische und logische Werte und Operatoren verwendet werden. ↩︎
-
Auch diese Wiederholung lässt sich äquivalent mit “bis” statt “solange” formulieren: Wiederhole bis n-te Stelle ≠
0oder n = 1: … ↩︎ -
Der Unteralgorithmus “stelle Code
0000” müsste ähnlich angepasst werden: Wiederhole solange n-te Stelle ≠ Startzeichen: … Wir sollten ihn dann auch allgemeiner in “stelle Startcode ein” umbenennen. ↩︎ -
Ein solches Verfahren wird in der Informatik als vollständige Suche, erschöpfende Suche oder auch Brute-Force-Verfahren (sinngemäß etwa “Holzhammermethode”) bezeichnet. ↩︎
3.1.1 Übungsaufgaben
Praktische Übungen
Aufgabe: Gewichte vergleichen
Gegeben sind N außerlich gleiche Säckchen, die Sand enthalten (die Anzahl N beträgt dabei mindestens 2). Eines der Säckchen enthält goldhaltigen Sand und ist daher etwas schwerer als die anderen. Alle anderen Säckchen sind gleich schwer. Sie erhalten eine Balkenwaage, mit der Sie das Gewicht von jeweils zwei Säckchen vergleichen können, um festzustellen, welches der beiden Säckchen schwerer ist bzw. ob beide Säckchen gleich schwer sind.
Ihr Aufgabe besteht nun darin, einen Algorithmus anzugeben, mit dem sich systematisch das Säckchen mit dem Goldanteil ermitteln lässt.
- Überlegen Sie dabei, welche Anweisungen und Abfragen hier sinnvoll sind.
- Beschreiben Sie Ihr Lösungsverfahren sprachlich möglichst eindeutig und allgemeingültig (das Verfahren soll für beliebige N ≥ 2 anwendbar sein).
Tool: In der folgenden interaktiven Simulation können Sie verschiedene Lösungsstrategien selbst durchspielen, um ein Lösungsverfahren zu entwickeln und zu testen. Ziehen Sie die Säckchen auf die freien Felder in der Waage, um ihr Gewicht zu vergleichen. Die Fläche in der Mitte können Sie nutzen, um die Säckchen während des Lösungsverfahrens zu verwalten (z. B. oben die noch nicht betrachteten Säckchen, unten die bereits betrachteten Säckchen). Das gesuchte Säckchen können Sie im grünen Feld rechts platzieren.
Klicken Sie auf “Lösung anzeigen”, wenn Sie glauben, das richtige Säckchen gefunden zu haben. Mit den anderen Schaltflächen lässt sich die Simulation neu starten und die Anzahl der Säckchen ändern.
3.2 Darstellung von Algorithmen
Motivation
Wir haben bisher verschiedene Möglichkeiten kennengelernt, um Algorithmen zu beschreiben: Zum einen in natürlicher Sprache, die allerdings Uneindeutigkeiten enthalten kann und es erschwert, einen Algorithmus wirklich präzise und eindeutig zu beschreiben. Auf der anderen Seite haben wir die Umsetzung als Programm in einer konkreten Programmiersprache, also die Implementierung eines Algorithmus in Form von Programmcode. Diese Darstellung ist zwar maximal eindeutig, da ihre Syntax und Semantik durch die verwendete Programmiersprache genau vorgegeben sind, für Menschen aber nur dann verständlich, wenn die entsprechende Programmiersprache beherrscht wird. Zwischen diesen beiden Welten liegt der sogenannte Pseudocode, also eine Beschreibung in natürlicher Sprache, die sich aber auf ganz bestimmte Formulierungen und Anweisungen beschränkt – etwa “wiederhole … bis”, “falls … dann … sonst …” – so dass eine Beschreibung entsteht, die schon relativ nah am Code einer textuellen imperativen Programmiersprache ist, dabei aber allgemeiner verständlich ist.
Um einen Algorithmus zu einer gegebenen Problemstellung zu entwickeln und darüber zu kommunizieren, kann es hilfreich sein, den Ablauf zunächst auf Papier zu entwerfen, bevor er in Scratch oder einer anderen Programmiersprache umgesetzt wird. Als Alternative zu einer textuellen Beschreibung gibt es auch Möglichkeiten, Algorithmen unabhängig von einer konkreten Programmiersprache grafisch darzustellen. Zwei verbreitete Darstellungsformen dafür sind Struktogramme und Programmablaufpläne.
Diese grafischen Darstellungen sind sowohl für das Lesen von Algorithmen als auch für den Algorithmenentwurf hilfreich: Zum einen sind sie durch ihre reduzierte, strukturierte Darstellung übersichtlicher und eindeutiger als Texte – zum anderen leiten sie uns durch ihre formalen Vorgaben und die zur Verfügung stehenden grafischen Grundbausteine dazu an, uns beim Algorithmenentwurf auf bestimmte Ablaufstrukturen zu beschränken.
Struktogramme
Struktogramme (auch nach ihren Entwicklern Nassi-Shneiderman-Diagramme genannt) sind Diagramme zur grafischen Beschreibung von Algorithmen.1 In einem Struktogramm werden rechteckige Blöcke als Grundbausteine verwendet, die gestapelt und ineinander geschachtelt werden können.
| Anweisung | |
|---|---|
 |
Einzelne elementare Anweisungen werden jeweils durch einen einfachen Block dargestellt, der mit der möglichst kurz und präzise formulierten Anweisung beschriftet ist. |
 |
Anweisungen, die Unterprogramme aufrufen, können durch einen Block mit zwei Seitenstreifen dargestellt werden, um sie von elementaren Anweisungen zu unterscheiden (hier in Anlehnung an Unterprogrammaufrufe in Scratch rot schattiert). |
| Sequenz | |
|---|---|
 |
Blöcke können vertikal zu größeren Blöcken gestapelt werden, so dass sich Sequenzen ergeben. |
Für die Kontrollstrukturen (Fallunterscheidungen und Wiederholungen) gibt es spezielle Blöcke, in die andere Blöcke eingepackt werden.
| Wiederholung | |
|---|---|
 |
Der Block für eine bedingte Wiederholung besteht aus einem |
 |
Bei Endloswiederholungen wird in der Regel die Beschriftung weggelassen und der Rahmen |
| Fallunterscheidung | |
|---|---|
 |
Der Block für eine Fallunterscheidung (“falls … dann … sonst …”) besteht aus einer Kopfzeile, in der die Bedingung steht, gefolgt von zwei Blöcken, die nebeneinander stehen: Links der Block, der ausgeführt wird, wenn die Bedingung erfüllt ist, rechts der Block, der anderenfalls ausgeführt wird (beide Bereiche können auch leer sein). |
 |
Bei rein bedingten Anweisungen (“falls … dann” ohne “sonst”) bleibt der rechte Teilblock leer. |
Die Blöcke innerhalb von Wiederholungen und Fallunterscheidungen können dabei einfache Anweisungsblöcke, Sequenzen oder komplexere, aus anderen Blöcken zusammengesetzte Teilalgorithmen sein.
Ihnen ist vermutlich schon aufgefallen, dass Struktogramme den aus Scratch bekannten, ebenfalls aus Blöcken zusammengesetzten Skripten stark ähneln – mit dem Hauptunterschied, dass die alternativen Anweisungen einer Fallunterscheidung nebeneinander gestellt werden statt übereinander.2 Die folgende Tabelle stellt zur Veranschaulichung ein paar Struktogramm-Beispiele den jeweiligen Umsetzungen in Scratch gegenüber:
| Grundstruktur | Darstellung im Struktogramm | Darstellung in Scratch |
|---|---|---|
| Anweisungssequenz | 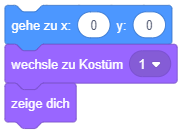 |
|
| Bedingte Wiederholung | 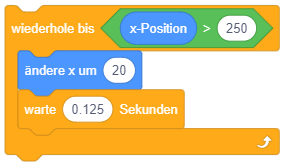 |
|
| Endloswiederholung | 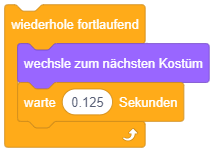 |
|
| Bedingte Anweisung (ohne Alternative) | 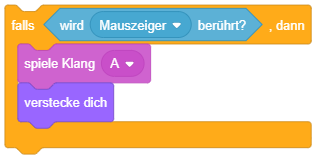 |
|
| Fallunterscheidung (Bedingte Anweisung mit Alternative) |
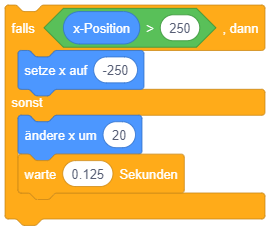 |
Beispiel: Code knacken
Betrachten wir noch einmal den einfachen Algorithmus zum Ermitteln der richtigen Kombination eines Zahlenschlosses aus dem vorigen Kapitel:
- Stelle Code
0000ein - Versuche Schloss zu öffnen
- Wiederhole bis Schloss offen ist:
- Stelle nächsten Code ein
- Versuche Schloss zu öffnen
Im Struktogramm wird der Algorithmus wie folgt dargestellt:
Die einzelnen Anweisungen werden durch entsprechend beschriftete Blöcke dargestellt, die gestapelt werden. Für die Wiederholung verwenden wir einen -förmigen Block, der mit der Wiederholungsbedingung “solange Schloss nicht offen ist” beschriftet ist und den Block der beiden zu wiederholenden Anweisungen enthält.
Varianten der Wiederholungen
Die Kontrollstruktur “Wiederholung” gibt es in verschiedenen Varianten, von denen wir ein paar bereits in Scratch kennengelernt haben: die Endloswiederholung, Wiederholung mit fester Anzahl und bedingte Wiederholung. An dieser Stelle werfen wir einen genaueren Blick auf diese verschiedenen Variante und grenzen sie voneinander ab.
Aus Scratch kennen wir die Endloswiederholung und die Wiederholung mit fester Anzahl (“wiederhole n-mal”) als Formen der Wiederholung ohne Bedingung.
Die aus Scratch bekannte bedingte Wiederholung ist eine Wiederholung mit Abbruchbedingung – sprachlich formuliert als “wiederhole bis Bedingung” – und wird folgendermaßen ausgeführt: Zuerst wird überprüft, ob die Bedingung erfüllt ist. Falls sie nicht erfüllt ist, wird der enthaltene Block einmal ausgeführt und anschließend erneut die Bedingung geprüft. Falls sie erfüllt ist, wird die Wiederholung beendet und das Programm fährt nach dem Wiederholungsblock fort.
Manchmal ist es aber intuitiver, eine Wiederholung stattdessen als “wiederhole solange Bedingung” zu formulieren. In diesem Fall erfüllt die Bedingung die Rolle einer Laufbedingung: Falls sie zu Beginn bzw. nach einem Durchlauf der Wiederholung erfüllt ist, wird ein weiterer Wiederholungsdurchlauf durchgeführt, anderenfalls wird die Wiederholung beendet (also genau entgegengesetzt zu einer Wiederholung mit Abbruchbedingung).3
Ein weiterer Unterschied besteht darin, ob die Lauf- oder Abbruchbedingung das erste Mal vor dem ersten Wiederholungsdurchlauf (bzw. zu Beginn einer Wiederholung) oder nach dem ersten Durchlauf (bzw. am Ende der Wiederholung) überprüft und ausgewertet wird. Bei den oben beschriebenen Varianten wird die Bedingung bereits zu Beginn einmal ausgewertet, weswegen sie im Block auch oben steht (im “Kopf” des Blocks). Diese Form der Wiederholung wird daher als kopfgesteuerte Wiederholung bezeichnet.
In Struktogrammen lassen sich auch fußgesteuerte Wiederholungen darstellen, bei denen die Bedingung nur am Ende jeden Durchlaufs geprüft wird – hier wird intuitiverweise ein -förmiger Block verwendet und die Bedingung ans Ende gestellt. Im Gegensatz zur kopfgesteuerten Wiederholung wird der enthaltende Block hier mindestens einmal ausgeführt, selbst wenn die Abbruchbedingung bereits zu Beginn erfüllt ist (bzw. die Laufbedingung bereits zu Beginn nicht erfüllt ist). Die kopfgesteuerte Wiederholung würde in diesem Fall gar nicht ausgeführt werden.
Die folgende Übersicht zeigt alle Varianten der Wiederholungen (kopf- oder fußgesteuert mit Lauf- oder Abbruchbedingung, Endloswiederholung und Wiederholung mit fester Anzahl), die sich in Struktogrammen darstellen lassen:
Für die bedingten Wiederholungen gilt: Ob kopf- oder fußgesteuerte Form, ob Lauf- oder Abbruchbedingung zur Formulierung eines Algorithmus am besten geeignet ist, hängt immer von der konkreten Situation ab. Manchmal kann eine der Varianten zu intuitiver verständlichen oder eleganter wirkenden Formulierungen führen. Es sollte allerdings beachtet werden, dass nicht alle Varianten in jeder Programmiersprachen direkt umsetzbar sind – in Scratch gibt es beispielsweise keine fußgesteuerten Wiederholungen – und daher bei der Implementierung eventuell umformuliert werden müssen.
Aufgabe: Geschirrspülmaschine leeren
Zur praktischen Veranschaulichung soll nun ein einfacher Algorithmus als Struktogramm entworfen werden. Als Problemstellung soll eine Geschirrspülmaschine ausgeräumt werden, die Tassen, Teller und Schüsseln enthält. Dabei sollen die verschiedenen Geschirrteile unterschiedlich behandelt werden:
Tassen sollen in den Schrank geräumt werden, alle anderen Geschirrteile ins Regal.
Geschirrteile, die beim Spülen kaputtgegangen sind, werden dagegen weggeworfen.
Dabei soll mitgezählt werden, wie viele Geschirrteile weggeworfen werfen.
Als Erstes legen wir fest, welche einfachen Anweisungen wir zur Formulierung des Lösungsverfahrens verwenden können, mit welchen Objekten gearbeitet wird und welche Eigenschaften der Objekte hier für uns relevant sind. Als problemspezifische Anweisungen reichen hier “nimm das nächste Teil aus der Spülmaschine”, “stelle das Teil in den Schrank”, “stelle das Teil ins Regal” oder “wirf das Teil weg”. Da wir außerdem zählen müssen, wie oft die Anweisung “wirf das Teil weg” ausgeführt wurde, verwenden wir zusätzlich eine Variable namens “Zähler” und als weitere Anweisungen Variablenzuweisungen wie “setze Zähler auf Wert” oder “erhöhe Zähler um Wert”.
Die naheliegenden Objekte, mit denen hier gearbeitet wird, sind hier die Geschirrteile, die wir aus der Spülmaschine nehmen. Uns interessieren nur zwei Attribute dieser Objekte: die Sorte (Tasse oder etwas anderes) und der Zustand (kaputt oder nicht). Außerdem müssen wir überprüfen können, ob die Spülmaschine leer ist oder nicht, um zu entscheiden, wann wir fertig sind.
Wir werden uns im Struktogramm also auf die folgenden elementaren Anweisungen, Variablenzuweisungen und Zustandsabfragen beschränken:
Nun geht es darum, die elementaren Anweisungen mit Hilfe von Kontrollstrukturen in den richtigen Ablauf zu bringen, wobei wir die Zustandsabfragen in den Bedingungen der Kontrollstrukturen verwenden werden.
Wir nähern uns Schritt für Schritt an die Lösung an, indem wir das Problem zunächst auf das Wesentliche reduzieren und Details wie das Zählen der weggeworfenen Geschirrteile erst einmal weglassen, um sie später zu unserer Lösung hinzuzufügen.
Wir beginnen also mit dem Grundgerüst: Es sollen nacheinander alle Geschirrteile aus der Spülmaschine genommen und verarbeitet werden, bis diese leer ist. Die Anweisung “nimm nächstes Teil” wird also innerhalb einer bedingten Wiederholung platziert. Als Abbruchbedingung wird geprüft, ob die Spülmaschine leer ist.
Wir ergänzen nun innerhalb des Blocks, der wiederholt ausgeführt wird, die eigentliche Verarbeitung der Geschirrteile. Es sollen unterschiedliche Aktionen durchgeführt werden, je nach Zustand und Sorte des zuletzt genommenen Objekts.
Als Erstes fügen wir also eine Fallunterscheidung zur Unterscheidung zwischen kaputten und nicht kaputten Objekten hinzu. Falls die Bedingung “ist kaputt?” erfüllt ist, soll die Anweisung “wirf weg” ausgeführt werden, die dazu in der linken Seite des Fallunterscheidungs-Blocks platziert wird.
In der rechten Seite des Fallunterscheidung-Blocks fügen wir nun den Block ein, der beschreibt, was im anderen Fall getan werden soll. Wenn das zuletzt genommene Objekt nicht kaputt ist, hängt es von seiner Sorte ab, was mit ihm gemacht werden soll.
Wir platzieren rechts also einen weiteren Fallunterscheidungs-Block, der als Bedingung prüft, ob das Objekt eine Tasse ist. Falls ja, soll die Anweisung “stelle in den Schrank” ausgeführt werden (links), anderenfalls die Anweisung “stelle ins Regal” (rechts).
Nun fehlt noch das Zählen der weggeworfenen Geschirrteile: Dazu ergänzen wir die Anweisung “erhöhe Zähler um 1” im linken Bereich der äußeren Fallunterscheidung, so dass sie zusätzlich zu “wirf weg” ausgeführt wird, wenn ein kaputtes Objekt aus der Spülmaschine genommen wurde. Der Vollständigkeit halber sollten wir den Zähler ganz zu Beginn noch auf 0 als Startwert setzen.
Das vollständige Struktogramm finden Sie unter “Schritt 4”. Es sind natürlich auch Variationen dieses Lösungsverfahrens möglich, z. B. könnten die Eigenschaften der Objekte auch in anderer Reihenfolge überprüft oder das Zählen der weggeworfenen Objekte auf andere Weise gelöst werden.
Fazit
Um einen Algorithmus als Struktogramm darzustellen, sind wir “gezwungen”, das Gesamtproblem in kleinere Teilprobleme zu zerlegen, bis nur noch Grundstrukturen wie Sequenzen und Kontrollstrukturen zur Lösung der Teilprobleme benötigt werden, die sich mit den Blöcken der Struktogramme darstellen lassen und zur Gesamtlösung zusammengebaut werden – ganz im Sinne der strukturierten Programmierung bzw. des “Computational Thinking”. Durch die Beschränkung auf diese einfachen Grundstrukturen lassen sich Algorithmen, die als Struktogramme formuliert werden, sogar in gewissem Maße automatisch in Programmcode verschiedener imperativer Programmiersprachen übersetzen.
Als Struktogramm formulierte Algorithmen lassen sich außerdem durch die Ähnlichkeit der Darstellung relativ einfach in Scratch implementieren – und andersherum Scratch-Programme sehr direkt als Struktogramme abstrakter skizzieren. Es kann also nützlich sein, Algorithmen, die später in Scratch umgesetzt werden sollen, zunächst auf Papier oder an der Tafel als Struktogramm zu entwickeln.
Struktogramme können mit Papier und Stift oder mit einem einfachen digitalen Zeichenwerkzeug wie LibreOffice Draw erstellt werden. Bequemer ist aber die Erstellung mit einem speziellen Struktogramm-Editor. Solche Tools sind oft auch in der Lage, automatisch Programmcode verschiedener Programmiersprachen aus dem erstellten Struktogramm zu erzeugen. Verweise auf Struktogramm-Editoren finden Sie in der Linksammlung bei den Software-Werkzeugen.
Programmablaufpläne
Programmablaufpläne (auch kurz “PAP”, engl. flowcharts) stellen eine weitere Möglichkeit zur grafischen Darstellung von Algorithmen dar, die sich deutlich von Struktogrammen unterscheidet. Hier werden Algorithmen als Graphen repräsentiert, die mögliche zeitliche Abfolgen von Anweisungen in einem Algorithmus abbilden. Die Knoten in diesem Graphen sind Anweisungen, Verzweigungen und Start-/Endzustände.
- Einzelne Anweisungen oder Unterprogrammaufrufe werden hier (wie bei Struktogrammen) durch Blöcke dargestellt, die mit der Anweisung beschriftet sind.
- Pfeile kennzeichnen den Übergang von einem Knoten zum nächsten. Ein Pfeil, der von einem Anweisungsblock ausgeht, gibt also beispielsweise an, mit welcher Anweisung als Nächstes fortgefahren wird.
- Verzweigungen werden durch Rauten dargestellt, die mit einer Bedingung beschriftet sind und von denen zwei Pfeile ausgehen. Sie repräsentieren Entscheidungen im Programmablauf, bei denen in Abhängigkeit von der angegebenen Bedingung entweder über den “ja”-Pfeil oder den “nein”-Pfeil fortgefahren wird.
- Start und Ende des Ablaufs werden durch kleine runde Knoten dargestellt. Jeder Algorithmus hat genau einen Startknoten, an dem der Ablauf beginnt.
Die folgende Tabelle stellt die grundlegenden Elemente dar, aus denen Programmablaufpläne bestehen:4
 |
 |
 |
 |
 |
| Start-/Endzustand | Anweisung | Unterprogrammaufruf | Übergang zum nächsten Element | Verzweigung |
Auffällig ist, dass es keine Grundbausteine für bedingte Anweisungen/Fallunterscheidungen oder bedingte Wiederholungen gibt wie bei Struktogrammen. Stattdessen werden diese Kontrollstrukturen alle mit Hilfe von Verzweigungen zusammengesetzt.
Der Ablauf eines Algorithmus kann für einen gegebenen PAP einfach nachvollzogen werden, indem vom Startknoten aus entlang der Pfeile gegangen wird und alle Anweisungen auf dem Weg ausgeführt werden. Bei jeder Verzweigung wird die in der Raute enthaltene Bedingung ausgewertet, um zu entscheiden, ob der mit “ja” beschriftete Pfeil oder der mit “nein” beschriftete Pfeil weiterverfolgt wird.
Damit ein Algorithmus, der als Programmablaufplan dargestellt wird, eindeutig ist, müssen ein paar Regeln eingehalten werden:
- Es muss genau einen Startknoten geben und mindestens einen Stopknoten.
- Von jedem Element des Programmablaufplans muss genau ein Pfeil ausgehen, der dieses Element mit dem als Nächstes auszuführenden Element verbindet. Einzige Ausnahmen sind Verzweigungen und Stopknoten.
- Von jeder Verzweigung gehen genau zwei Pfeile aus, von denen einer mit “ja” und der andere mit “nein” (oder “wahr” und “falsch”) beschriftet ist.
- Von Stopknoten gehen keine Pfeile aus, der Ablauf des Algorithmus endet hier also, da nicht weitergangen werden kann.
Mit diesen wenigen Elementen lassen sich alle bisher behandelten Kontrollstrukturen darstellen:
- Fallunterscheidungen bestehen aus einer Verzweigung, die den Ablauf in zwei parallele Abläufe aufteilt (der “wenn”-Fall und der “sonst”-Fall), die anschließend wieder zusammenführen.
- Wiederholungen entstehen, wenn Pfeile einen Kreis bilden. Üblicherweise muss hier am Beginn (bei einer kopfgesteuerten Wiederholung) oder am Ende (bei einer fußgesteuerten Wiederholung) dieses Kreises eine Verzweigung stehen, die es ermöglicht, in Abhängigkeit von einer Abbruchbedingung aus dem Kreis auszusteigen. Anderenfalls erhalten wir eine Endloswiederholung.
Die folgende Tabelle stellt die bekannten Kontrollstrukturen anhand von Beispielen als PAP dar und stellt sie zum Vergleich den jeweiligen Struktogrammen und Umsetzungen in Scratch gegenüber:
| Grundstruktur | Darstellung im PAP | Darstellung als Struktogramm | Darstellung in Scratch |
|---|---|---|---|
| Anweisungssequenz |  |
||
| Bedingte Wiederholung |  |
||
| Endloswiederholung |  |
||
| Bedingte Anweisung (ohne Alternative) |  |
||
| Fallunterscheidung (Bedingte Anweisung mit Alternative) |
 |
Beispiel: Code knacken
Auch hier soll als erstes Beispiel der einfache Algorithmus zum Ermitteln der richtigen Zahlenschloss-Kombination als Programmablaufplan untersucht werden:
Auf den Startknoten – den Beginn des Algorithmus – folgt eine Sequenz von zwei Anweisungen, die jeweils durch Pfeile miteinander verbunden sind. Anschließend folgt mit der bedingten Wiederholung der eigentlich interessante Teil: Hier wird eine Verzweigung verwendet, in der die Abbruchbedingung der Wiederholung “ist Schloss offen?” überprüft wird. Falls das der Fall ist, endet der Algorithmus: Der mit “ja” beschriftete Pfeil aus der Verzweigung wird also mit einem Stopknoten verbunden. Anderenfalls soll die Sequenz der beiden Anweisungen “stelle nächsten Code ein” und “versuche Schloss zu öffnen” ausgeführt werden. Der mit “nein” beschriftete Pfeil führt daher zur ersten dieser beiden Anweisungen und von dieser ein Pfeil zur nächsten. Nach der zweiten Anweisung soll erneut die Abbruchbedingung ausgewertet werden: Der von ihr ausgehende Pfeil führt daher wieder zur Verzweigung zurück.
Ablaufsimulation
Die folgenden Bilder stellen einen möglichen Ablauf dieses Algorithmus dar (die richtige Kombination lautet hier 0815):
Wir beginnen im Startknoten, der eindeutig festgelegt ist.
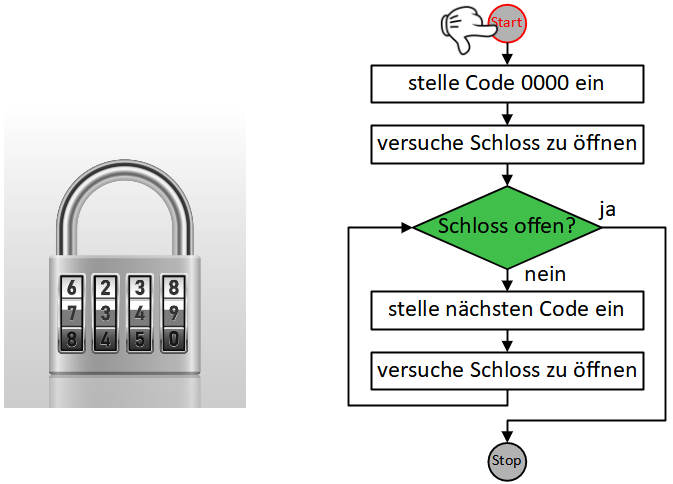
Vom Startknoten aus gehen wir entlang des Pfeils zur nächsten Anweisung und führen diese aus.
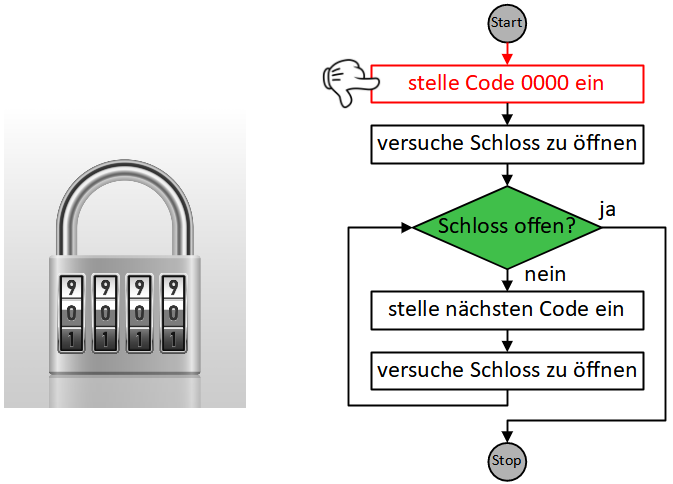
Von dieser Anweisung gehen wir wieder entlang des Pfeils zur Folgeanweisung und führen diese ebenfalls aus.
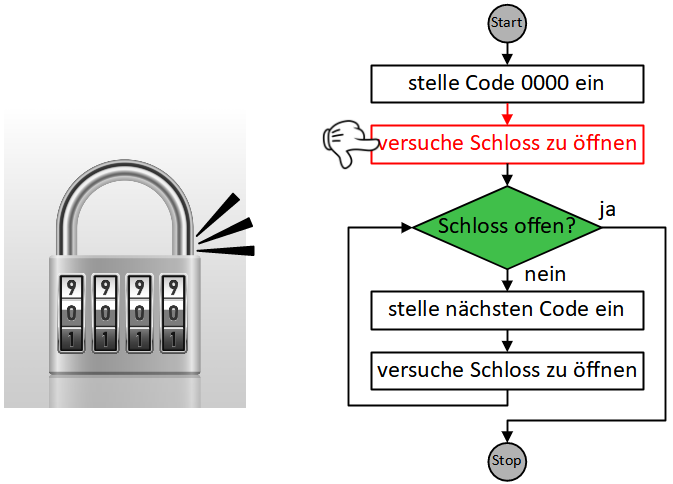
Wir erreichen eine Verzweigung: Nun wird die darin enthaltene Bedingung ausgewertet, die zu diesem Zeitpunkt nicht erfüllt ist.
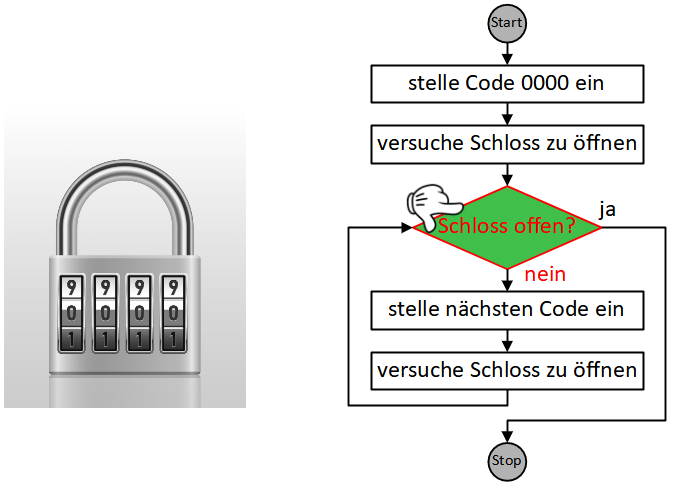
Also verfolgen wir den mit “nein” beschrifteten Pfeil zur nächsten Anweisung, die ausgeführt wird.
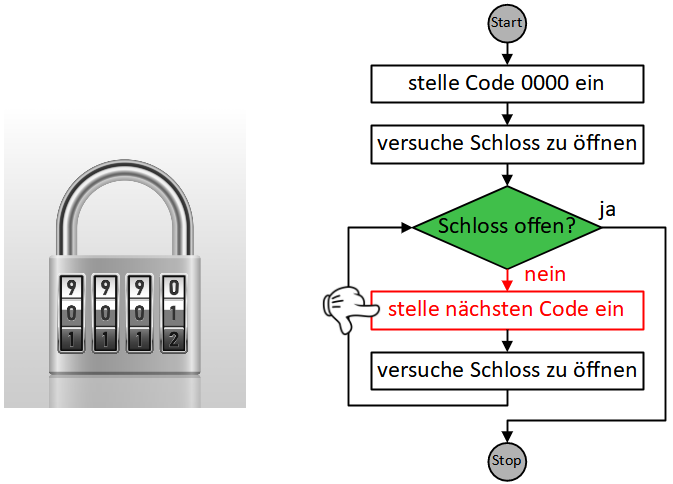
Von dieser Anweisung gehen wir wieder entlang des Pfeils zur Folgeanweisung und führen diese ebenfalls aus.
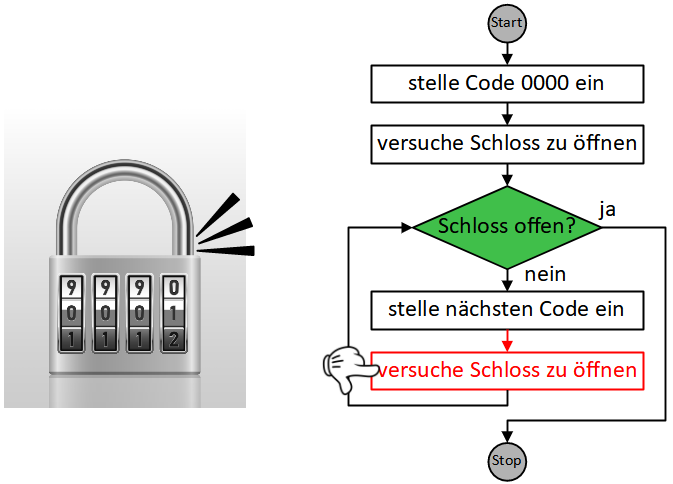
Über den Pfeil erreichen wir nun wieder die Verzweigung zu Beginn des Wiederholung und überprüfen ihre Bedingung erneut.
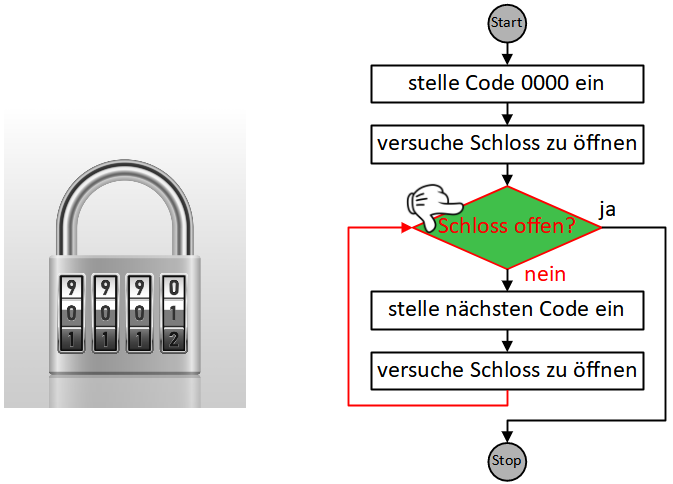
Es vergehen nun einige Schritte, bis wir im 2446. Schritt die Kombination 0814 erreichen und überprüfen.
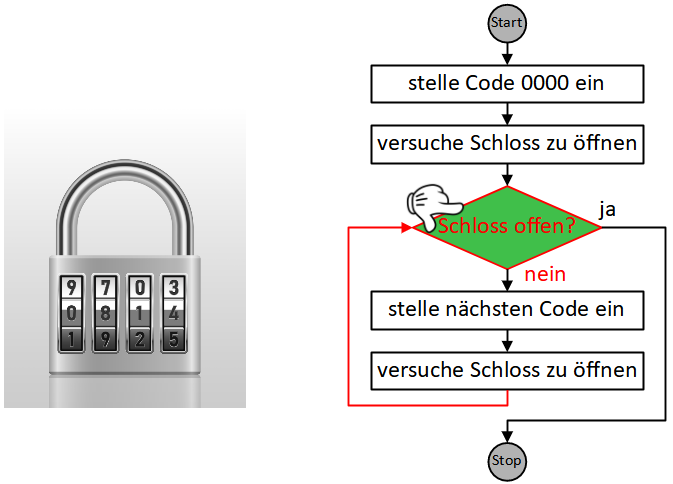
Da die Bedingung momentan nicht erfüllt ist wird entlang des “nein”-Pfeils gegangen und die nächste Anweisung ausgeführt.
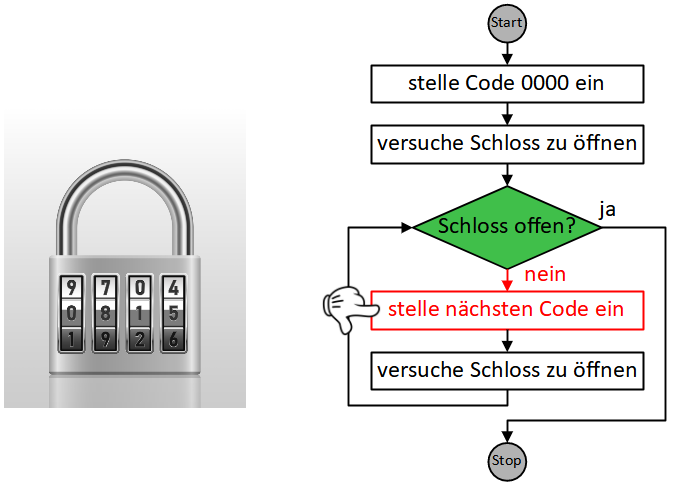
Die Ausführung der folgenden Anweisung öffnet das Schloss, da 0815 hier die richtige Kombination ist.
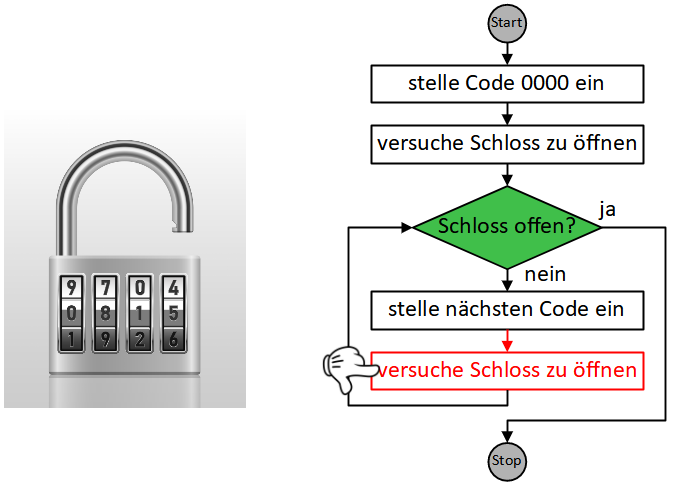
Wir kehren zur Verzweigung zu Beginn des Wiederholung zurück und überprüfen ihre Bedingung, die nun erfüllt ist.
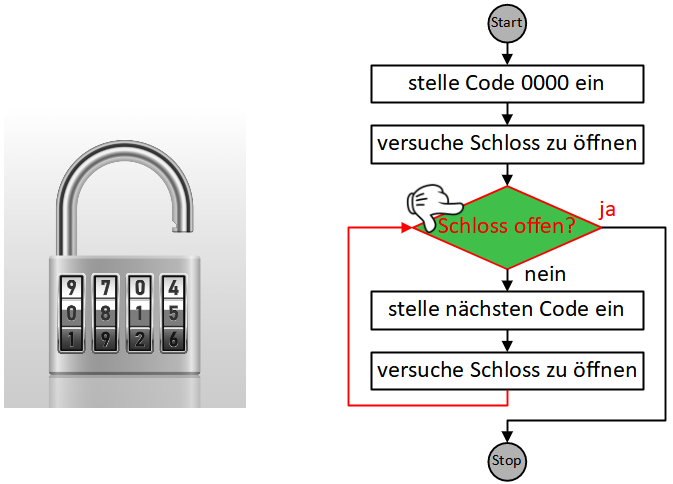
Also verfolgen wir den mit “ja” beschrifteten Pfeil und erreichen den Stopknoten. Der Algorithmus endet an dieser Stelle.
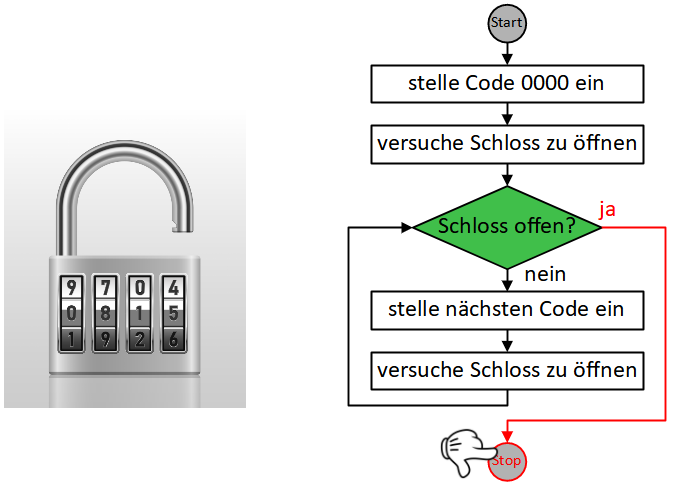
An diesem Beispielalgorithmus ist erkennbar, dass eine Wiederholung in einem PAP durch eine Verzweigung beschrieben wird, von der ein Weg ausgeht, der später wieder zu dieser Verzweigung zurückführt. Als Nächstes werden wir uns genauer ansehen, wie die verschiedenen üblichen Kontrollstrukturen in Programmablaufplänen umgesetzt werden.
Fallunterscheidungen im PAP
Bedingte Anweisungen und Fallunterscheidungen werden in Programmablaufplänen durch Verzweigungen umgesetzt, die zu zwei parallelen Wegen führen, die später wieder zusammenlaufen:
Bei einer bedingten Anweisung ohne Alternative enthält der Weg, von dem der “nein”-Pfeil ausgeht, keine weiteren Anweisungen:
Bei mehrfachen Fallunterscheidungen enthält dieser Weg dagegen weitere Verzweigungen in parallele Wege, die später mit dem “Hauptweg” zusammengeführt werden:
Wiederholungen im PAP
Generell werden Wiederholungen in Programmablaufplänen durch Verbindungen von Elementen mittels Pfeilen umgesetzt, die einen Weg bilden, der im Kreis läuft.
Bei bedingten Wiederholungen enthält dieser Kreis mindestens eine Verzweigung, die es ermöglicht, in Abhängigkeit von einer Abbruchbedingung aus dem Kreislauf auszubrechen:
Bei einer Wiederholung mit Laufbedingung (statt Abbruchbedingung) verläuft der Kreis vom “ja”-Pfeil aus, während der “nein”-Pfeil aus dem Kreis ausbricht:
Bei einer Endloswiederholung gibt es dagegen einen Weg ohne Verzweigung, der im Kreis führt:
Aufgabe: Geschirrspülmaschine leeren
Im Folgenden wird noch einmal der Algorithmus aus dem Beispiel Geschirrspülmaschine leeren betrachtet und Schritt für Schritt als Programmablaufplan formuliert. Dazu gehen wir von einem möglichen Ablauf des Algorithmus aus und untersuchen, welche Anweisungen nacheinander ausgeführt werden und welche Entscheidungen dabei gefällt werden müssen.
Als Erstes muss überprüft werden, ob die Spülmaschine leer ist, um zu entscheiden, was als Nächstes gemacht werden soll. Der Startknoten wird also durch einen Pfeil mit einer Verzweigung mit der Bedingung “Spülmaschine ist leer?” verbunden.
Falls die Bedingung erfüllt ist, sind wir fertig. Der “ja”-Pfeil der Verzweigung führt also zum Stopknoten. Anderenfalls soll das nächste Geschirrteil aus der Spülmaschine genommen werden.
Um zu entscheiden, was mit dem genommenen Geschirrteil gemacht werden soll, muss anschließend überprüft werden, ob das Teil kaputt ist oder nicht. Dazu wird eine weitere Verzweigung eingeführt, deren Bedingung in diesem Fall “Teil ist kaputt?” lautet.
Falls es kaputt ist, soll es weggeworfen werden und anschließend mit dem nächsten Geschirrteil (wenn vorhanden) weitergemacht werden. Dazu wird der “ja”-Pfeil der Verzweigung mit der Anweisung “wirf weg” verbunden, die wiederum zurück zur Verzweigung führt, in der geprüft wird, ob die Spülmaschine weitere Teile enthält.
Anderenfalls soll es entweder in den Schrank oder ins Regal gestellt werden, je nachdem, ob eine Tasse oder ein anderes Geschirrteil genommen wurde. Dazu wird eine weitere Verzweigung eingeführt, die als Bedingung “Teil ist Tasse?” prüft.
Tassen werden in den Schrank gestellt: Der “ja”-Pfeil der Verzweigung führt also zur Anweisung “stelle in Schrank”. Da anschließend mit dem nächsten Geschirrteil weitergemacht werden soll, führt der ausgehende Pfeil von dieser Anweisung zurück zur Verzweigung “Spülmaschine ist leer?”.
Andere Geschirrteile werden ins Regal gestellt: Der “nein”-Pfeil der Verzweigung führt also zur Anweisung “stelle ins Regal”. Auch diese Anweisung verweist anschließend zurück zur Verzweigung “Spülmaschine ist leer?”.
Abschließend müssen noch die Anweisungen zum Zählen der weggeworfenen Geschirrteile ergänzt werden: Zu Beginn (zwischen Startknoten und erster Verzweigung) wird der Zähler auf den Startwert 0 gesetzt und direkt nach dem Wegwerfen eines Geschirrteils um 1 erhöht.
Den vollständigen Programmablaufplan finden Sie unter “Schritt 8”. Wie beim Entwurf des Struktogramms sind auch hier andere Abläufe möglich.
Fazit
Anhand von Programmablaufplänen lässt sich die Ausführung von Algorithmen intuitiver nachvollziehen als bei Struktogrammen. Sie verfolgen einen anderen Ansatz beim Entwurf von Algorithmen, da hier vom Ablauf ausgegangen wird statt von der Struktur des Algorithmus. Allerdings erfordert der Entwurf von Algorithmen mit PAP eine gewisse Disziplin: Umfangreichere Algorithmen können schnell chaotisch und unübersichtlich werden und es können leicht uneindeutige Diagramme entstehen, wenn Kanten fehlen oder zu viele Kanten eingezeichnet werden.
Ein Problem von Programmablaufplänen ist, dass hier mit Sprüngen gearbeitet wird: Der Kontrollfluss kann von jeder Anweisung zu jeder beliebigen anderen Anweisung übergehen. Dadurch lassen sich Abläufe darstellen, die mit den üblichen Kontrollstrukturen gar nicht direkt beschreibbar sind und sich auch nicht in jeder Programmiersprache implementieren lassen.5 In Struktogrammen sind die möglichen Abläufe dagegen auf die üblichen Kontrollstrukturen eingeschränkt.
-
Die Elemente von Nassi-Shneiderman-Diagrammen sind in Deutschland genormt in DIN 66261. ↩︎
-
Tatsächlich sind blockbasierte visuelle Programmiersprachen wie Scratch, Snap! oder Blockly unübersehbar von Struktogrammen zur grafischen Darstellung von Algorithmen als Vorbild inspiriert. ↩︎
-
Jede Wiederholung mit Laufbedingung kann in eine Wiederholung mit Abbruchbedingung umformuliert werden und umgekehrt, indem die Lauf- bzw. Abbruchbedingung einfach negiert wird – z. B. ist “wiederhole bis Ziel erreicht” gleichbedeutend mit “wiederhole solange Ziel nicht erreicht”. ↩︎
-
Die grafischen Elemente von Programmablaufplänen sind genormt in DIN 66011, gemeinsam mit den ähnlichen Elementen von Datenflussplänen. ↩︎
-
Um Programmablaufpläne uneingeschränkt in einer Programmiersprache implementieren zu können werden sogenannte Sprunganweisungen benötigt, die es erlauben, den Kontrollfluss an einer beliebigen anderen Stelle im Programm fortzusetzen. Sprunganweisungen gelten in der imperativen Programmierung aber als tendenziell fehleranfällig, da sie dazu verleiten, unübersichtlichen und schwer überprüfbaren Programmcode zu schreiben. ↩︎
3.2.1 Übungsaufgaben
Praktische Übungen
Aufgabe 1: Scratch-Skript als Struktogramm
Setzen Sie das folgende Scratch-Skript in ein Struktogramm mit gleicher Bedeutung um:
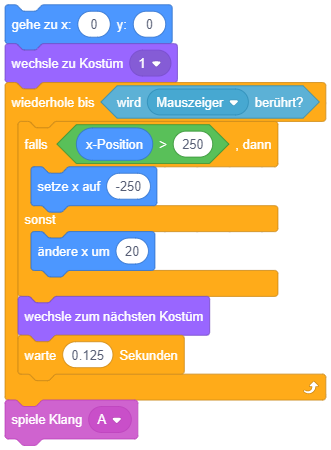
Formulieren Sie die Anweisungen im Struktogramm dabei ähnlich wie in den Scratch-Blöcken, z. B.:
gehe zu Position (0, 0) wechsle zu Kostüm 1
Aufgabe 2: Struktogramm aufstellen
Erstellen Sie ein Struktogramm, das den Ablauf eines Würfelspiels nach den folgenden Regeln beschreibt:
Sie starten mit 0 Punkten und würfeln wiederholt mit einem Würfel, bis Sie genau 21 Punkte erreicht haben.
Sie erhalten dabei bei jedem Wurf 1 bis 6 Punkte, je nachdem, wie viele Augen Sie gewürfelt haben.
Wenn Sie dabei 21 Punkte überschreiten, fallen Sie wieder auf 0 zurück.
Beschränken Sie sich dabei möglichst auf die folgenden ausführbaren Anweisungen (Zahl ist hierbei ein frei wählbarer Parameter):
würfle setze Punkte auf Zahl erhöhe Punkte um Zahl
Kontrollstrukturen und Variablenzuweisungen können aber wie üblich ohne Einschränkung verwendet werden, wenn nötig.
Verwenden Sie in den Vergleichen für die Bedingungen die Begriffe “Punkte” und “Würfelergebnis” für den Wert des aktuellen Punktestands bzw. die Anzahl der im letzten Wurf gewürfelten Augen.
Aufgabe 3: Programmablaufplan interpretieren
Der folgende Programmablaufplan beschreibt einen Algorithmus zur Steuerung einer Figur in einer 2D-Welt (jeder Schritt bewegt die Figur auf ein angrenzendes Feld).
- Vollziehen Sie den Ablauf des Algorithmus nach und zeichnen Sie den Weg, den die Figur während der Ausführung zurücklegt.
- Übersetzen Sie den Programmablaufplan anschließend in ein Struktogramm, das denselben Algorithmus beschreibt.
Aufgabe 4: Programmablaufplan aufstellen
Erstellen Sie einen Programmablaufplan zur Steuerung eines Staubsaugroboters, der nach den folgenden Regeln durch den Raum fährt:
Nach dem Start fährt der Roboter schrittweise geradeaus.
Wenn er dabei auf eine Wand stößt, fährt er einen Schritt zurück und dreht sich in eine zufällige Richtung, bevor er weitermacht.
Wenn der Akkuladestand unter 10% sinkt, stoppt der Roboter.
Im Programmablaufplan sollten möglichst nur die folgenden Anweisungen und Zustandsabfragen (für Bedingungen und Vergleiche) verwendet werden, die der Roboter ausführen kann:
| Anweisungen | Zustandsabfragen |
|---|---|
| fahre einen Schritt vor fahre einen Schritt zurück drehe dich zufällig | wird Wand berührt? Akkuladestand (in %) |
Aufgabe 5: Gewichte vergleichen
Formulieren Sie den Algorithmus, den Sie in der Aufgabe Gewichte vergleichen aus der vorigen Übung entwickelt haben, jeweils als Struktogramm und Programmablaufplan.

Vergleichen Sie beide Darstellungen: Welche empfanden Sie als einfacher zu entwickeln? Welche ist übersichtlicher oder leichter zu verstehen? Welche eignet sich besser, um den Ablauf des Algorithmus nachzuvollziehen?
Aufgabe 6: Algorithmische Grundstrukturen
In dieser Aufgabe sollen gegebene Programmablaufpläne auf die darin enthaltenden algorithmischen Grundstrukturen hin untersucht werden:
- Ermitteln Sie für jeden der folgenden Programmablaufpläne an, welche der Ihnen bekannten grundlegenden Kontrollstrukturen (bedingte Wiederholung, Endloswiederholung und/oder Fallunterscheidung) jeweils darin wiederzufinden sind.
- Übersetzen Sie die Programmablaufpläne dann jeweils in Struktogramme mit der gleichen Bedeutung, sofern möglich.
| Programmablaufplan 1 | Programmablaufplan 2 | Programmablaufplan 3 |
|---|---|---|
3.3 Anhang
3.3.1 Diagramme zur Algorithmendarstellung
Struktogramme
Übersicht über die Grundbausteine von Nassi-Shneiderman-Diagrammen (“Struktogramme”), genormt in DIN 66261 (siehe Wikipedia):
| Algorithmische Grundstruktur | Darstellung im Struktogramm |
|---|---|
| Anweisung |  |
| Sequenz |  |
| Endloswiederholung |  |
| Wiederholung mit fester Anzahl |  |
| Bedingte Wiederholung1 (kopfgesteuert) |  |
| Bedingte Wiederholung1 (fußgesteuert) |  |
| Bedingte Anweisung |  |
| Bedingte Anweisung mit Alternative |  |
| Mehrfache Fallunterscheidung |  |
| Unterprogrammaufruf2 (ggf. mit Argumenten) |  |
Programmablaufpläne
Übersicht über die Grundbausteine von Programmablaufplänen (“PAP”, flowcharts), genormt in DIN 66001 (siehe Wikipedia):
 |
 |
 |
 |
 |
| Start-/Endzustand | Anweisung | Unterprogrammaufruf | Übergang | Verzweigung |
Darstellung einfacher Beispiele zu den algorithmischen Grundstrukturen als Programmablaufpläne (an jeder Stelle, an der hier eine einzelne Anweisung steht, kann auch ein komplexerer Unteralgorithmus stehen):
| Algorithmische Grundstruktur | Darstellung im Programmablaufplan |
|---|---|
| Sequenz |  |
| Bedingte Anweisung |  |
| Bedingte Anweisung mit Alternative |  |
| Bedingte Wiederholung3 (“wiederhole bis”, kopfgesteuert) |  |
| Bedingte Wiederholung3 (“wiederhole bis”, fußgesteuert) |  |
| Endloswiederholung |  |
-
Die Abbruchbedingung “wiederhole bis” kann hier auch ersetzt werden durch eine Laufbedingung “wiederhole solange”. ↩︎ ↩︎
-
Dieser Baustein ist nicht in DIN 66261 genormt und kann alternativ auch als Anweisung dargestellt werden. ↩︎
-
Um eine Wiederholung mit Laufbedingung (“wiederhole solange”) statt Abbruchbedingung (“wiederhole bis”) umzusetzen, muss hier nur die Beschriftung der Kanten “ja” und “nein” getauscht werden. ↩︎ ↩︎
4. Netzwerke & Internet
4.1 Netzwerke und Internet
Das Online-Skript zum Thema “Netzwerke und Internet” befindet sich zur Zeit noch im Aufbau.
4.2 Kommunikationsprotokolle
Protokolle stellen ein zentrales Konzept in der Netzwerkkommunikation dar. Jeder Ablauf und jeder Nachrichtenaustausch – sei es das Abrufen und Versenden von E-Mails mit einem Mailprogramm, das Öffnen einer Webseite im Webbrowser oder ein Sprachchat während eines Onlinespiels – wird durch Protokolle geregelt. Aber was genau wird in der Informatik unter einem Protokoll verstanden – was ist und was macht ein Protokoll und wie lässt es sich formal beschreiben?
Protokolle
Im alltäglichen Sprachgebrauch kennen wir verschiedene Bedeutungen des Begriffs “Protokoll”: In einem Versuchsprotokoll werden die Einzelschritte, Beobachtungen und Ergebnisse eines wissenschaftlichen Versuchs festgehalten, ein Verlaufsprotokoll dokumentiert Ablauf, Beiträge und Beschlüsse einer Sitzung, während ein diplomatisches Protokoll Vorschriften über den Ablauf von Staatsbesuchen festlegt. Allgemein lässt sich sagen: In einem Protokoll wird aufgezeichnet oder vorgegeben, zu welchem Zeitpunkt oder in welcher Reihenfolge welcher Vorgang durch wen oder was veranlasst wird.
Damit Informatiksysteme miteinander kommunizieren können (das heißt: Informationen austauschen können), muss genau festgelegt werden,
- welche Nachrichten verschickt werden und was sie bedeuten,
- in welchem Format die Nachrichten dargestellt werden und wie sie codiert werden,
- in welcher Reihenfolge welche Nachrichten verschickt werden dürfen
- und welche Aktionen beim Verschicken oder Empfangen bestimmter Nachrichten ausgeführt werden.
Diese Regeln werden durch Kommunikationsprotokolle festgelegt.
In der Informatik ist ein Kommunikationsprotokoll also eine Vereinbarung, wie Datenübertragung zwischen mehreren Systemen abläuft. Ein Protokoll wird durch Regeln definiert, die Syntax (also Form), Semantik (also Bedeutung) und Synchronisation (also Reihenfolge und Taktung) der Kommunikation festlegen. Die Spezifikation des Protokolls ist ein Dokument, in dem diese Regeln formal beschrieben werden. Ein Netzwerkprotokoll ist wiederum ein Protokoll, das die Kommunikation in Rechnernetzwerken beschreibt, z. B. im Internet.
Beispiel: Im Café
Um die verschiedenen Aspekte eines Kommunikationsprotokolls anschaulich nachzuvollziehen, werden wir uns ein kleines (hier natürlich stark reduziertes) Alltagsbeispiel ansehen: das Verkaufsgespräch in einem Café. In diesem Café gelten allerdings strikte Regeln, wie Gespräche zwischen Kund*innen und Bedienungen ablaufen. Jedes Gespräch wird dadurch begonnen, dass die Kundin mit einem “Hallo?” Kontakt zur Bedienung aufnimmt, die wiederum, wenn sie bereit ist, mit “Hallo!” antwortet.
Die Kundin hat nun mehrere Möglichkeiten: Sie kann verschiedene Artikel aus den Artikelgruppen (z. B. Getränke, Kuchen oder Snacks) bestellen oder sie kann sich darüber informieren, welche Artikel es jeweils in einer Gruppe gibt. Diese Aktionen können beliebig oft und in beliebiger Reihenfolge durchgeführt werden. In jedem Fall wartet die Kundin anschließend auf die Antwort der Bedienung: Im Normalfall eine Bestätigung (z. B. “OK!”, “Mal sehen!”) und je nach Anfrage eine Liste von Artikelnamen oder der gewünschte Artikel selbst.
Das Gespräch wird durch die Kundin mit “Tschüß!” beendet und von der Bedienung mit “Tschüß!” bestätigt. Danach steht die Bedienung wieder für ein Gespräch mit anderen Kund*innen bereit, ebenfalls wieder eingeleitet mit “Hallo?”. Das Bild zeigt einen möglichen Gesprächsverlauf:1
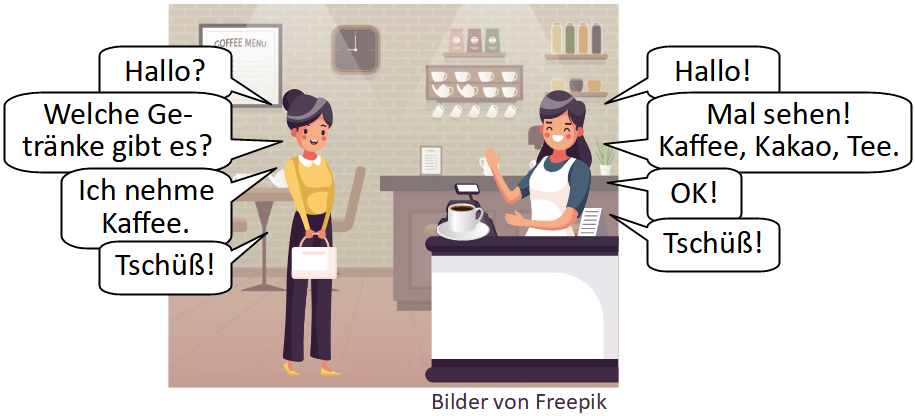
Beginnt die Kundin dagegen gleich mit einer Anfrage ohne das Gespräch zuvor mit “Hallo?” einzuleiten, reagiert die Bedienung mit einem genervten “Häh?!”, da das Protokoll für Verkaufsgespräche hier nicht eingehalten wurde:

In diesem Szenario kann sich die Bedienung nur jeweils um eine Person zur Zeit kümmern. Wenn also eine Kundin mit “Hallo?” Kontakt aufnehmen möchte, während sich die Bedienung gerade im Gespräch mit einer anderen Kundin befindet, so lehnt sie die Anfrage mit der Antwort “Bin beschäftigt!” ab, statt ein weiteres Gespräch zu beginnen:

Sequenzdiagramme
Um den Ablauf des Nachrichtenaustauschs für Kommunikationsbeispiele grafisch formal darzustellen, werden meist Sequenzdiagramme verwendet. Diese Diagramme enthalten vertikale Zeitlinien für alle Kommunikationspartner, zwischen denen Nachrichten ausgetauscht werden. Jede Nachricht wird durch einen beschrifteten Pfeil repräsentiert, der vom Absendezeitpunkt auf der Zeitlinie des Senders zum Empfangszeitpunkt auf der Zeitlinie des Empfängers verläuft. Auf diese Weise lässt sich der zeitliche Ablauf der Kommunikation nachvollziehen, indem die Nachrichten von oben nach unten entlang der Pfeile gelesen werden.
Um zu kennzeichnen, dass ein Kommunikationspartner nach dem Absenden einer Anfrage wartet, bis er eine Antwort vom anderen System empfangen hat, kann in die Zeitlinie ein Balken eingezeichnet werden, der den Wartezeitraum markiert (siehe linke Zeitlinie in der Abbildung).
Client-Server-Kommunikation
Das folgende Sequenzdiagramm stellt den Nachrichtenaustausch für das erste Gespräch im Café noch einmal anschaulich dar:
Der im Beispiel dargestellte Ablauf ist typisch für eine Client-Server-Kommunikation: Der Client (“Kunde”) muss zunächst eine Sitzung (engl. session) mit dem Server (“Bedienung”) beginnen, die durch eine “Begrüßung” oder Anmeldung eingeleitet wird (hier die Anfrage “Hallo?”). Der Server bestätigt diese Anfrage und eröffnet somit die Sitzung, oder er lehnt sie ab (hier beispielsweise wenn er gerade mit einem anderen Client beschäftigt ist). Anschließend stellt der Client während der Sitzung eine oder mehrere Anfragen, die vom Server beantwortet werden, und er beendet die Sitzung abschließend mit einer “Verabschiedung” oder Abmeldung (hier die Nachricht “Tschüß!”), die wiederum vom Server bestätigt wird.
Oft merkt der Server sich während einer Sitzung mit einem Client zusätzliche Informationen über diese Sitzung (z. B. mit wem er gerade kommuniziert oder welche Aktionen während der Sitzung durchgeführt werden). Sitzungen sind aber nicht zwingend notwendig für Client-Server-Kommunikation bzw. Kommunikation zwischen Systemen im Allgemeinen.
Die Nachrichten des Clients stellen in dieser Kommunikation überwiegend Anfragen dar, auf die der Server mit Bestätigungen oder Fehlermeldungen antwortet. Dabei werden in einigen Fällen auch weitere Informationen oder Objekte mitgeliefert – hier beispielsweise die angefragte Liste der vorhandenen Getränke oder die bestellte Tasse Kaffee. Auf der technischen Ebene werden solche Daten in der Netzwerkkommunikation als Nutzdaten (engl. payload) bezeichnet: Nutzdaten sind also Teile einer Nachricht, die keine direkte Steuer- oder Protokollinformation enthalten, sondern weitere zu übermittelnde Informationen darstellen, z. B. HTML-Dokumente, Bilder oder Datensätze, die vom Client angefragt wurden oder auf den Server hochgeladen werden sollen.
Ausnahmebehandlung
Ein Kommunikationsprotokoll muss ebenfalls genau festlegen, wie mit Fehlern und Ausnahmesituationen umgegangen wird – also beispielsweise mit Anfragen, die nicht beantwortet werden können, unverständlichen Anfragen oder Nachrichten, die in einer anderen Reihenfolge als im Protokoll vorgesehen verschickt werden. In der Client-Server-Kommunikation antwortet der Server auf ungültige Anfragen des Clients in der Regel mit unterschiedlichen Fehlermeldungen.
Die folgenden Beispiele zeigen, welche Ausnahmesituationen bei der Kommunikation im Café auftreten könnten. Zum einen könnte die Kundin einen Artikel bestellen, der nicht vorhanden ist. In diesem Fall antwortet die Bedienung mit der spezifischen Fehlermeldung “Gibt’s nicht!” und das Gespräch geht weiter:
Zum anderen könnte die Kundin eine komplett unvorhergesehene Anfrage stellen, die laut Protokoll keinen Sinn macht. Hier antwortet die Bedienung mit der generischen Fehlermeldung “Häh?!”:
Eine weitere Ausnahmesituation wurde oben bereits gezeigt: Wenn die Bedienung eine Anfrage von einer Kundin erhält, während sie sich gerade in einer Sitzung mit einer anderen Person befindet, antwortet sie mit der spezifischen Fehlermeldung “Bin beschäftigt!” – so weiß die Kundin, dass sie es zu einem späteren Zeitpunkt noch einmal versuchen sollte:
Eine andere Situation ergibt sich, wenn die Bedienung nach einem Gespräch einschläft (oder in der Realität: wenn ein Server zwischenzeitlich ausfällt oder abgeschaltet wird). In diesem Fall wird die Kundin auf eine Anfrage wie “Hallo?”, um ein Gespräch zu beginnen, gar keine Antwort erhalten. In der Praxis werden solche Situationen in der Regel dadurch gelöst, dass ein Client nur eine gewisse Dauer (z. B. maximal 5 Sekunden) auf eine Antwort des Servers wartet, bevor eine Zeitüberschreitung (engl. timeout) auftritt und der Client den Wartevorgang abbricht. Anschließend kann er die Anfrage entweder erneut abschicken oder die Kommunikation abbrechen:
Timeouts können aber auch während einer Sitzung mit laufendem Server auftreten – bei der Kommunikation im Internet beispielsweise dann, wenn Datenpakete einer Anfrage auf dem Übertragungsweg verlorengehen.
Protokollspezifikation
Fassen wir also einmal die Spezifikation des Café-Protokolls zusammen, indem der generelle Ablauf einer Sitzung beschrieben wird und alle Nachrichten mit den jeweils möglichen Folgenachrichten aufgelistet werden.
Wir beginnen mit den Nachrichten zur Steuerung der Sitzungen:
- Eine Sitzung wird mit der Anfrage “Hallo?” vom Client eingeleitet.
- Der Server bestätigt mit “Hallo!” , falls er bereit ist, eine neue Sitzung zu beginnen.
- Anderenfalls lehnt er die Sitzung ab und antwortet mit der Fehlermeldung “Bin beschäftigt!”.
- Eine Sitzung wird durch die Nachricht “Tschüß!” vom Client beendet.
- Der Server bestätigt das Ende der Sitzung mit “Tschüß!”.
Der Server befindet sich hier also immer in einem von zwei Zuständen:
- bereit: Der Server hat momentan keine laufende Sitzung, kann also eine neue Sitzung annehmen.
- beschäftigt mit Client X: Der Server befindet sich momentan in einer Sitzung mit Client X.
Während einer Sitzung kann der Client die folgenden Anfragen beliebig oft und in beliebiger Reihenfolge verschicken:
- Der Client kann mit der Nachricht “Welche Name der Artikelgruppe gibt es?” die verfügbaren Artikel einer Artikelgruppe (z. B. Getränke, Kuchen oder Snacks) abfragen.
- Der Server antwortet mit der Bestätigung “Mal sehen!” und der Liste der Artikelnamen (als Nutzdaten), wenn die Artikelgruppe bekannt ist.
- Anderenfalls antwortet er mit der Fehlermeldung “Gibt’s nicht!”.
- Der Client kann mit der Nachricht “Ich nehme Name des Artikels.” einen Artikel kaufen.
- Der Server bestätigt mit “OK!” und dem gewünschten Artikel (als Nutzdaten), falls dieser bekannt und vorhanden ist.
- Anderenfalls antwortet er auch hier mit der Fehlermeldung “Gibt’s nicht!”.
Wenn sich der Server gerade im Zustand “beschäftigt mit Client X” befindet, antwortet er auf alle Anfragen anderer Clients mit der Fehlermeldung “Bin beschäftigt!”.
In allen anderen Fällen – also auf unverständliche (das heißt: falsch formatierte) oder unbekannte (das heißt: im Protokoll nicht spezifizierte) Anfragen oder Anfragen zum falschen Zeitpunkt (z. B. “Tschüß!” ohne dass eine Sitzung läuft) – antwortet der Server mit der generischen Fehlermeldung “Häh?!”.
Wie Sie vielleicht bereits festgestellt haben, sieht das Protokoll der Einfachheit halber keine Bezahlung von bestellten Artikeln vor – in diesem Café ist alles umsonst. Anderenfalls müsste das Protokoll um weitere Nachrichten, mögliche Abläufe, Ausnahmebehandlungen und Fehlermeldungen zum Bezahlen ergänzt werden.
Ähnlich werden auch reale Protokolle für die Kommunikation zwischen Informatiksystemen beschrieben, wobei diese Spezifikationen natürlich deutlich technischer und umfangreicher sind. Hier spielen beispielsweise – je nach Aufgabenbereich des Protokolls – auch Aspekte wie die digitale Codierung der Daten, erwartete Datentypen und Wertebereiche von Anfrageparametern oder die physikalische Umsetzung der Datenübertragung eine Rolle.2
Protokolle in der Praxis
Das Café-Beispiel ist zwar anschaulich, aber auch etwas künstlich, da alltägliche Kommunikation normalerweise nicht nach strikten syntaktischen Regeln abläuft. Für ein realistischeres Szenario könnte etwa die Kommunikation mit einem IT-System, z. B. einem Geld- oder Ticketautomaten oder einem einfachen Sprachassistenzsystem betrachtet werden.
Generell werden Kommunikationsprotokolle in der Praxis verwendet, um die Datenübertragung zwischen Informatiksystemen zu regeln und Standards aufzustellen, auf die in der Entwicklung von Kommunikationssystemen zurückgegriffen werden kann. So regeln etwa Druckprotokolle den Datenaustausch zwischen einem Rechner und einem Drucker, um digitale Dokumente auszudrucken, während Netzwerkprotokolle den Datenaustausch in Rechnernetzen beschreiben – womit sie eine der Grundlagen des Internets darstellen. Bekannte Anwendungsprotokolle im Internet sind etwa HTTP, das verwendet wird, wenn Sie über ihren Webbrowser Dokumente von einem Webserver herunterladen, oder Protokolle wie POP3 oder IMAP zum Abrufen von E-Mails von einem Mailserver.
Reale Protokolle unterscheiden sich dabei sehr stark in ihren Zielen und ihrer Komplexität: So gibt sehr beispielsweise sehr einfache Druckprotokolle, die nur die reinen Druckdaten übermitteln, während umfangreichere Druckprotokolle auch Aspekte wie Datenkompression und -verschlüsselung, Fehlerkorrektur oder Auftragssteuerung nach Priorität, Druckkosten und -dauer mit berücksichtigen.
Protokollarchitektur
Dieser Abschnitt befindet sich noch im Aufbau.
Sender-Empfänger-Modell
Zur Beschreibung von Kommunikationsprozessen wird hier das Sender-Empfänger-Modell verwendet – ein einfaches Kommunikationsmodell, das den Austausch von Nachrichten zwischen zwei Systemen, dem Sender und dem Empfänger, beschreibt. Die Nachrichten sind Daten bzw. codierte Informationen, die vom Sender zum Empfänger über ein physikalisches Übertragungsmedium geschickt werden. In einem typischen Kommunikationsablauf nehmen die Kommunikationspartner abwechselnd die Rolle von Sender und Empfänger an.
Informationen werden dabei mittels physikalischer Signale übertragen, beispielsweise durch elektrische, optische oder akustische Signale oder elektromagnetische Wellen. Technisch gesehen übermittelt der Sender das Signal in Form einer physikalischen Größe (z. B. Spannung oder Strom bei elektrischen Signalen) an den Empfänger, der das eingehende Signal misst und interpretiert.
Beispiel: Morse-Schach
Protokollstapel
Ein Protokollstapel ist in der Datenübertragung eine Architektur von Kommunikationsprotokollen, in der Protokolle als Schichten übereinander angeordnet sind. Jede Schicht nutzt zur Erfüllung ihrer Aufgaben die Funktionen (Dienste) der jeweils darunterliegenden Schicht und stellt der jeweils über ihr liegenden Schicht ihre Dienste bereit.
Ausblick: Internetprotokollstapel
Zur Einordnung der Netzwerkprotokolle für die Kommunikation im Internet wird der Internetprotokollstapel verwendet. Hier werden die Protokolle in vier Schichten eingeteilt: Anwendungsschicht, Transportschicht, Internetschicht (auch: Vermittlungsschicht) und Netzzugangsschicht.
- Anwendung: Die Protokolle dieser Schicht beschreiben, wie Anwendungsprogramme auf verschiedenen Rechnern miteinander kommunizieren (z. B. ein Webbrowser mit einem Webserver, oder ein Mailprogramm mit einem Mailserver).
- Transport: Die Protokolle dieser Schicht beschreiben, wie die End-Kommunikationspartner (also Anwendungen auf den Endgeräten) Daten austauschen, unabhängig vom anwendungsspezifischen Inhalt der Nachrichten. Diese Art der Kommunikation wird als Ende-zu-Ende-Kommunikation bezeichnet – hierbei spielt es keine Rolle, auf welchem Weg die Datenpakete einer Nachricht durch das Netzwerk kommen.
- Internet/Vermittlung: Im Internet sind die miteinander kommunizierenden Endgeräte in der Regel nicht direkt verbunden, sondern befinden sich meist in verschiedenen Netzwerken, die über viele Zwischengeräte verbunden sind. Die Protokolle dieser Schicht beschreiben, wie ein Datenpaket von Punkt zu Punkt durch die Netzwerke gelangt. Ein wichtiger Bestandteil dieser Protokolle ist die Wegefindung (Routing).
- Netzzugang: Die Protokolle dieser Schicht beschreiben, wie Daten zwischen Geräten ausgetauscht werden, die sich im selben Netzwerkabschnitt befinden, also direkt per Kabel, WLAN oder Verteiler miteinander verbunden sind. Diese Schicht beinhaltet die Übertragungsschicht, deren Protokolle beschreiben, wie Binärdaten zwischen zwei direkt verbundenen Systemen über ein physikalisches Medium übertragen werden.
-
Dieses und die folgenden Bilder wurden erstellt unter Verwendung von Grafiken von Freepik. ↩︎
-
Um eine Vorstellung davon zu bekommen, können Sie einmal einen Blick in die Spezifikation des Protokolls HTTP (Hypertext Transfer Protocol) werfen, das beschreibt, wie Anwendungsdaten im Internet ausgetauscht werden (z. B. um Webseiten mit einem Webbrowser abzurufen): https://datatracker.ietf.org/doc/html/rfc7540 ↩︎
4.3 Netzwerke
Grundlagen und Aufbau
Das Internet ist ein “Netzwerk von Netzwerken” bzw. konkreter ein hierarchisch aufgebautes Netzwerk aus verschiedenen Geräten. Die kleinsten Netzwerke stellen dabei die sogenannten lokalen Netzwerke dar.
LAN
Ein lokales Netzwerk (engl. local area network oder kurz LAN) ist in der Regel ein Netzwerk, das sich auf eine kleinere räumliche Umgebung beschränkt, etwa einen privaten Haushalt (“Heimnetz”), eine Schule oder Firma. Ein LAN ist üblicherweise kabelgebunden, ein drahtloses lokales Netzwerk, in dem die Geräte per Funk kommunizieren, wird dagegen als WLAN (engl. wireless LAN) bezeichnet.1
Netzwerkkomponenten
Sehen wir uns dazu zunächst die Geräte an, aus denen solche Netzwerke – beispielsweise auch das Netzwerk bei Ihnen zuhause – zusammengesetzt sind, und welche verschiedenen Funktionen sie erfüllen.
Wir finden hier zunächst einmal Geräte wie PCs, Laptops und Smartphones, also die Endgeräte, mit denen Sie interagieren, beispielsweise um auf das Internet zuzugreifen. Eventuell kommunizieren aber auch Geräte innerhalb des lokalen Netzwerks direkt untereinander, z. B. wenn Sie einen Netzwerkdrucker verwenden, der von allen Rechnern im LAN gemeinsam genutzt wird.
Router und Modem
In Ihrem Heimnetzwerk befindet sich üblicherweise ein Gerät, das als Router bezeichnet wird, über das alle anderen Geräte miteinander kommunizieren können und das gleichzeitig die Schnittstelle “nach außen”, also ins Internet darstellt.2
Um den Router mittels z. B. DSL, Glasfaser oder Kabelnetz mit dem Internet zu verbinden (oder genauer gesagt: mit der Vermittlungsstelle bei Ihrem Internetdienstanbieter) wird ein weiteres Gerät benötigt: das Modem. Mittlerweile enthalten die meisten Router-Geräte (insbesondere wenn Sie von Ihrem Internetdienstanbieter zur Verfügung gestellt werden) aber bereits ein integriertes Modem.
An einen solchen Router können üblicherweise mehrere Endgeräte per LAN-Kabel oder drahtlos per Funk angeschlossen werden.3 Inzwischen sind die meisten Router, die in Heimnetzen zum Einsatz kommen, WLAN-tauglich, unterstützen also auch drahtlose Verbindungen. Die folgende Abbildung stellt die Vorder- und Rückseite eines handelsüblichen DSL-Routers mit WLAN (also eines WLAN-tauglichen Routers mit integriertem DSL-Modem) dar:4


Hier lassen sich 4 Endgeräte per LAN-Kabel (über die 4 gelben Anschlüsse rechts) und beliebig viele weitere per Funk anschließen. Über den linken Anschluss wird das Gerät mit dem DSL-Anschluss verbunden, über den das Internet erreichbar wird.
Was aber, wenn weitere Endgeräte per LAN-Kabel an das Gerät angeschlossen werden sollen? Oder wenn Sie ganz auf einen Router verzichten und stattdessen ein lokales Netzwerk ohne Internetanbindung einrichten möchten?
Switch
Um mehrere Geräte direkt miteinander zu verbinden, gibt eine weitere Komponente in Netzwerken: den sogenannten Switch, den sie vielleicht aus dem Computerraum Ihrer Schule kennen. Über ein Switch lassen sich einfach mehrere Endgeräte (oder auch weitere Switches) in der Regel über LAN-Kabel zusammenschließen, so dass sie untereinander kommunizieren können. Sie bilden dann einen Teil eines Netzwerks bzw. ein Netzwerksegment. So könnte beispielsweise ein Switch mit 5 LAN-Anschlüssen verwendet werden, um jeweils 4 Rechner mit einem LAN-Anschluss eines Routers (oder eines weiteres Switches) zu verbinden:
Die folgende Abbildung zeigt handelsübliche Switches verschiedener Größe (5 bis 24 LAN-Anschlüsse pro Switch), die für kleinere Heimnetze oder größere Firmennetzwerke geeignet sind:5

Ein drahtloser Switch (also ein Switch, mit dem sich Geräte per Funk verbinden können) wird üblicherweise als (Wireless) Access Point (engl. für “(drahtloser) Zugangspunkt”, kurz AP) bezeichnet.
Router als Multifunktionsgerät
Was ist nun der Unterschied zwischen einem Router-Gerät wie dem oben dargestellten DSL-Router, an den ja auch mehrere Endgeräte angeschlossen werden können, und einem Switch? Strenggenommen stellt ein Router im eigentlichen Sinne nur die Verbindung zwischen verschiedenen Netzwerken her – also beispielsweise zwischen Ihrem Heimnetz und dem Netzwerk Ihres Internetdienstanbieters oder zwischen mehreren lokalen Netzwerken innerhalb eines größeren Unternehmens.6 Ein Switch verbindet dagegen Geräte innerhalb eines lokalen Netzwerks.
Tatsächlich ist in so gut wie alle umgangssprachlich als “Router” bezeichneten Geräte auch ein Switch (und in WLAN-Router zusätzlich ein Access Point) integriert, damit sich mehrere Geräte mit dem Router verbinden können. Das oben dargestellte Gerät besteht also in Wirklichkeit aus vier Komponenten: Es kombiniert einen Router, einen Switch mit Anschlüssen für 4 Endgeräte, einen Access Point für WLAN, sowie ein DSL-Modem.

Der “Router”, der bei Ihnen im Wohnzimmer, Büro oder im Computerraum Ihrer Schule steht, kann aber noch viel mehr: Diese Geräte beinhalten in der Regel auch einen Server, auf dem verschiedene Anwendungsdienste laufen – zum Beispiel DNS zur Übersetzung von URLs in IP-Adressen oder DHCP zur automatischen Vergabe von IP-Adressen an Geräte im lokalen Netzwerk. Oft läuft auf dem Gerät auch ein kleiner Webserver, so dass Sie im Browser über die IP-Adresse des Routers eine grafische Benutzeroberfläche aufrufen können, über die das Netzwerk konfiguriert werden kann.
Üblicherweise enthalten Router daneben auch Sicherheitskomponenten wie etwa eine Firewall, die unerwünschte Zugriffe auf das Netzwerk blockiert (dazu mehr im Kapitel “Netzwerksicherheit”).
Zusammenfassung
Fassen wir also abschließend auf einer abstrakteren Ebene die verschiedenen Komponenten und ihre Rollen in Netzwerken zusammen und grenzen sie voneinander ab:7
| Ein Switch verbindet Geräte zu einem Netzwerksegment und erlaubt es ihnen, untereinander Daten auszutauschen. | |
| Ein Router (auch: Vermittlungsrechner) verbindet verschiedene Netzwerke miteinander (z. B. verschiedene LAN untereinander oder ein LAN mit dem Internet). | |
| Ein Modem stellt die Verbindung zwischen Routern über weite Übertragungswege her (z. B. per DSL, Glasfaser oder Kabelnetz). | |
| Ein Endgerät bildet den Netzabschluss und stellt in der Regel die Schnittstelle zur Benutzerin/zum Benutzer dar, ohne selbst notwendiger Bestandteil des Netzes zu sein (z. B. ein PC, Smartphone oder Netzwerkdrucker). | |
| Ein Server ist ein Endgerät, auf dem hauptsächlich Anwendungen laufen, die auf Anfragen von Client-Anwendungen auf anderen Endgeräten warten und diese über das Netwzerk beantworten. |
Die kleinsten lokalen Netzwerke – die Netzwerksegmente – bestehen nur aus Switches (bzw. APs) und Endgeräten, sowie ggf. einer Schnittstelle zu einem Router, der es mit der Außenwelt verbindet. Diese Routerschnittstelle wird als Gateway (engl. für “Ein-/Ausfahrtstor”) des lokalen Netzwerks bezeichnet. Mittels Routern (und Modems) werden kleinere Netzwerke hierarchisch zu komplexeren, weiträumigeren Netzwerken verbunden – von kleinen lokalen Nerkwerken (LAN) über städteumfassenden “Metropolitan Area Networks” (MAN) und länderumfassende “Wide Area Networks” (WAN) bis hin zu weltumspannenden “Global Area Networks” (GAN), die das Internet bilden.
Adressierung im Netzwerk
IP-Adressen
Eine der wichtigsten Aufgaben des Internetprotokolls (IP) besteht darin, einzelne Geräte im Netzwerk zu finden. Dazu muss jedes Gerät im Netzwerk mit einer eindeutigen Adresse identifiziert werden, die als IP-Adresse bezeichnet wird. Diese Adressen liegen als Bitfolgen aus Einsen und Nullen vor, damit sie von digitalen Geräten möglichst einfach verarbeitet werden können.
Im Protokoll IPv4 ist jede IP-Adresse 32 Bit (= 4 Byte) lang. Der besseren Lesbarkeit halber werden diese Bitfolgen üblicherweise in Dezimalpunktschreibweise (engl. dotted decimal notation) angegeben: Hierbei wird jedes Byte in eine Dezimalzahl umgewandelt und die Zahlen mit einem Punkt dazwischen notiert, z. B. 192.168.1.20 statt 11000000 10101000 00000001 00010100.
Subnetze
Eine wichtige Voraussetzung für diese Adressen ist, dass sie hierarchisch aufgebaut sind, damit an ihnen abgelesen werden kann, zu welchem Netzwerkbereich sie gehören – ähnlich einer Telefonnummer, die aus Ländervorwahl, Ortsvorwahl und Rufnummer besteht. Eine IP-Adresse beginnt dazu mit einem Netzwerkteil (quasi die “Vorwahl”), gefolgt von einem Geräteteil (die “Rufnummer”). Die Werte der Netzwerkteil-Bits sind dabei für alle Adressen innerhalb desselben Netzwerks festgelegt (und damit für alle Geräte im Netzwerk identisch), während die Werte der Geräteteil-Bits frei wählbar sind. Ein solcher zusammengehöriger Netzbereich innerhalb eines größeren Netzwerks, der einen abgeschlossenen IP-Adressbereich verwendet, wird auch als Subnetz bezeichnet. Subnetze können in weitere Subnetze unterteilt werden. Lokale Netzwerke (LAN) bzw. Netzwerksegmente stellen dabei die kleinsten Subnetze dar.
Ein IP-Adressbereich lässt sich in Kurzform in Präfixnotation angeben, also durch die erste IP-Adresse im Bereich, gefolgt von der Länge des Netzwerkteils in Bit (die sogenannte Präfixlänge), z. B. 192.168.1.0/24 für den Adressbereich von 192.168.1.0 bis 192.168.1.255.
Beispiel:
Für die Uni Kiel ist der IP-Adressbereich von 134.245.0.0 bis 134.245.255.255 registriert. Alle Adressen beginnen mit 134.245 bzw. mit der Bitfolge 10000110 11110101. Die ersten 16 Bit stellen hier den Netzwerkteil dar, an dem erkannt werden kann, dass es sich um eine Adresse der Uni Kiel handelt. Die Präfixnotation dieses Bereich lautet demnach 134.245.0.0/16.
Innerhalb dieses Adressbereichs können weitere Teilbereiche unterschiedlicher Größe festgelegt werden: So könnte beispielsweise der Bereich 134.245.10.0 bis 134.245.10.255 für das lokale Netzwerk der Unibibliothek reserviert sein (in Präfixnotation 134.245.10.0/24). Für dieses Subnetz stellen die ersten 24 Bit den Netzwerkteil dar, alle Adressen im Subnetz der Unibibliothek beginnen also mit 134.245.10 bzw. mit der Bitfolge 10000110 11110101 00001010.
Bei der Einrichtung eines Netzwerks wird jedem Endgerät eine IP-Adresse aus dem Adressbereich des Netzwerks zugewiesen. Dabei muss jedem Gerät eine unterschiedliche IP-Adresse zugewiesen werden, damit die Geräte im Subnetz eindeutig identifiziert werden können.
Die erste und letzte Adresse aus dem Netzwerk-Adressbereich werden nicht vergeben, da sie Sonderbedeutungen haben: Die erste Adresse steht für das Netzwerk selbst (“Netzwerkadresse”), die letzte Adresse ist die sogenannte Broadcast-Adresse. Pakete, die an diese Adresse verschickt werden, werden an alle Geräte im Netzwerk weitergeleitet statt an ein bestimmtes.
Die Größe eines Adressbereich lässt sich direkt aus der Präfixlänge berechnen: Beim Subnetz 134.245.10.0/24 mit einer Präfixlänge von 24 Bit (= Länge des Netzwerkteils) bleiben 8 Bit übrig (= Länge des Geräteteils), die frei wählbar sind, also umfasst das Subnetz 28 = 256 Adressen (von denen max. 254 an Geräte vergeben werden können). Das Subnetz 134.245.0.0/20 umfasst dagegen 212 = 4096 Adressen, da 12 Bit auf den Geräteteil entfallen.
Subnetzmaske
Der Adressbereich für ein Subnetz wird oft auch mit Hilfe der sogenannten Subnetzmaske angegeben: eine Bitfolge mit derselben Länge wie die IP-Adressen, die mit einer bestimmten Anzahl von 1-Bits beginnt, gefolgt von 0-Bits. Die 1-Bits geben an, welche Bits der IP-Adresse fest sind (der Netzwerkteil), während die 0-Bits angeben, welche Bits frei gewählt werden können (der Geräteteil).
Jedes Gerät im Netzwerk kennt seine eigene IP-Adresse sowie die Subnetzmaske und kann daraus den Adressbereich seines Subnetzes ermitteln. Die Subnetzmaske wird üblicherweise im selben Format angegeben wie die IP-Adresse, bei IPv4 also in Dezimalpunktschreibweise.
Beispiel 1: Einem Gerät im Netzwerk wurde die IP-Adresse 192.168.1.20 zugewiesen. Die Subnetzmaske lautet 255.255.255.0.
Um den Adressbereich des Netzwerks zu ermitteln, betrachten wir die Binärdarstellung der Subnetzmaske: 11111111 11111111 11111111 00000000. Das bedeutet, die ersten 24 Bit (= 3 Byte) sind bei allen Adressen im Netzwerk gleich, die letzten 8 Bit können frei gewählt werden. Jede IP-Adresse in diesem Subnetz beginnt also mit 192.168.1., gefolgt von einer Zahl zwischen 0 und 255. Die Netzwerkadressen umfassen also den Bereich 192.168.1.0 bis 192.168.1.255.
Die Adresse 192.168.1.0 steht für das Netzwerk selbst, die Adresse 192.168.1.255 für einen Broadcast im Netzwerk. Es können also bis zu 254 IP-Adressen für Geräte im Netzwerk vergeben werden, nämlich die Adressen 192.168.1.1 bis 192.168.1.254.
Beispiel 2: Einem Gerät im Netzwerk wurde die IP-Adresse 134.245.180.100 zugewiesen. Die Subnetzmaske lautet 255.255.240.0.
Um den Adressbereich des Netzwerks zu ermitteln, betrachten wir die Binärdarstellung der Subnetzmaske: 11111111 11111111 11110000 00000000. Das bedeutet, die ersten 20 Bit (= 2 Byte und die ersten 4 Bit des 3. Bytes) sind bei allen Adressen im Netzwerk gleich, die letzten 12 Bit können frei gewählt werden.
Hier ist es etwas komplizierter, den Adressbereich zu ermitteln. Die ersten beiden Byte sind fest, die Netzwerkadresse beginnt also mit 134.245. Beim nächsten Byte sind die ersten 4 Bit fest. Die Binärdarstellung der Dezimalzahl 180 lautet 10110100. Die erste 8-Bit-Binärzahl, die mit 1011 beginnt, ist 10110000 (dezimal 176), die letzte ist 10111111 (dezimal 191). Das letzte Byte kann komplett frei gewählt werden. Die Netzwerkadressen umfassen hier also den Bereich 134.245.176.0 bis 134.245.191.255.
Private Netzwerke
Die folgenden IP-Adressbereiche sind für private Netzwerke reserviert:
- 192.168.0.0 - 192.168.255.255 (umfasst 65 536 Adressen)
- 172.16.0.0 - 172.31.255.255 (umfasst ca. 1 Mio. Adressen)
- 10.0.0.0 - 10.255.255.255 (umfasst ca. 16,7 Mio. Adressen)
Private Netzwerke können wiederum in Subnetze aufgeteilt werden (z. B. ein privates Netzwerk mit dem Adressbereich 192.168.0.0/16 in 256 Subnetze mit jeweils 256 Adressen).
Diese IP-Adressen sind nicht global eindeutig, sondern können in beliebig vielen lokalen Netzwerken vorkommen. Da sie nicht eindeutig sind, können diese Adressen nicht über lokale Netzwerkgrenzen hinaus, also auch nicht im Internet geroutet werden. Stattdessen werden Rechner, die solche privaten IP-Adressen haben, im Internet durch die IP-Adresse ihres Gateway-Routers repräsentiert.
MAC-Adressen
…
Eine MAC-Adresse entspricht also in etwa der Personalausweis-ID einer Person: Sie ist global eindeutig, fest mit der Person verbunden und unveränderlich. Die IP-Adresse entspricht dagegen der Postadresse einer Person: Sie ist hierarchisch aufgebaut (Land, PLZ/Ort, Straße, Hausnummer, Name am Briefkasten), gibt Ausschluss darüber, wo sich eine Person befindet und ändert sich, wenn die Person umzieht. Beide Adressierungsarten können unter verschiedenen Umständen nützlich sein.
-
Im englischen Sprachraum ist dagegen der Begriff “Wi-Fi” statt “WLAN” für Funknetzwerke üblich, während dieser Begriff im deutschen Sprachraum nur für den Standard verwendet wird, der die in WLAN genutzte Funkübertragung beschreibt. ↩︎
-
Bekannte Modelle, die sich vielleicht auch in Ihrem Haushalt oder in Ihrer Schule wiederfinden, sind etwa die FRITZ!Box oder die Vodafone EasyBox. ↩︎
-
Der Begriff “LAN-Kabel” wird allgemein für Kabel zum Verbinden von Geräten in Rechnernetzen verwendet. Üblicherweise sind damit aber konkret Ethernet-Kabel gemeint. Ethernet ist dabei die Bezeichnung für eine Technik und das dazugehörige Protokoll zur kabelgebundenen Datenübertragung (analog zu WLAN oder “Wi-Fi” für Funkverbindungen). ↩︎
-
Quelle: Website von AVM, Produktseite FRITZ!Box 7530 ↩︎
-
Quelle: Website von D-Link, Produktseite D-LINK DGS-1100 ↩︎
-
Router werden daher auch als “Vermittlungssrechner” bezeichnet, weil sie zwischen verschiedenen Netzwerken vermitteln. ↩︎
-
Die hier verwendeten Grafiken stammen aus der Lernsoftware Filius (siehe Linksammlung) und werden dort zur Repräsentation der Komponenten Switch, Router (in Filius: Vermittlungsrechner), Modem und Client-Rechner (in Filius: Notebook) verwendet. ↩︎
4.4 Kommunikation im Netzwerk
Kommunikation im Subnetz
Bei der Konfiguration eines lokalen Netzwerks wird jedem Endgerät eine eindeutige IP-Adresse im Adressbereich des Subnetzes zugewiesen. Außerdem kennt jedes Gerät die Subnetzmaske und in der Regel die IP-Adresse des Gateway-Routers im lokalen Netzwerk, der die Schnittstelle nach außen darstellt (sofern vorhanden). Diese Informationen können beispielsweise manuell von der Person festgelegt werden, die das lokale Netzwerk administriert (“Netzwerkadmin”).
Jedes Endgerät in einem Netzwerksegment kennt üblicherweise alle anderen Endgeräte, die sich im selben Segment befinden. Konkret bedeutet das, dass auf jedem Endgerät eine Tabelle der IP-Adressen und zugehörigen MAC-Adressen aller Geräte im Subnetz gespeichert ist – die sogenannte ARP-Tabelle (auch “ARP Cache”, siehe Address Resolution Protocol). In einem Router können mehrere ARP-Tabellen gespeichert sein, je eine für jedes Netzwerksegment, mit dem er verbunden ist.
Das Versenden von Datenpaketen innerhalb des Subnetzes findet größtenteils über Protokolle der Netzzugangsschicht statt – da hier keine Wegefindung über Netzwerkgrenzen hinaus stattfindet, werden die entsprechenden Protokolle der Internetschicht (Vermittlungsschicht) nicht benötigt.
Wenn ein Endgerät eine Nachricht (konkreter: ein IP-Paket) an eine bestimmte Ziel-IP-Adresse verschicken möchte, kann es anhand der Subnetzmaske erkennen, ob das Ziel im selben Subnetz liegt: In diesem Fall stimmt der Netzwerkteil der eigenen IP-Adresse mit dem Netzwerkteil der Ziel-IP-Adresse überein. Ist das der Fall, schaut das sendende Gerät in seiner ARP-Tabelle unter der Ziel-IP-Adresse nach, um die Ziel-MAC-Adresse zu ermitteln. Dann verpackt es die Nachricht in ein Paket der Netzzugangsschicht, adressiert es mit der eigenen MAC-Adresse als Absender und der MAC-Adresse des Ziels als Empfänger und übertragt es.
Switching
Wenn Sender und Empfänger direkt verbunden sind, wird das Paket direkt übertragen. Wenn das Paket dagegen bei einem Switch ankommt, muss dieser entscheiden, an welchen seiner Ausgänge er das Paket weiterleitet – er muss also wissen, hinter welchem Ausgang das Gerät mit der Ziel-MAC-Adresse steckt. Diese Information ist in einer internen Tabelle des Switches gespeichert (Switching-Tabelle). Kennt der Switch die Ziel-MAC-Adresse nicht, leitet er das Paket einfach an alle Ausgänge weiter (alle Geräte, die das Paket empfangen und feststellen, dass die Ziel-MAC-Adresse nicht mit ihrer eigenen MAC-Adresse übereinstimmt, ignorieren das Paket).
Um einem Switch beizubringen, welche MAC-Adressen im Netzwerksegment vorhanden sind und wo die Geräte liegen, gibt es zwei Möglichkeiten: statisch oder dynamisch. Bei der statischen Variante trägt die Person, die das lokale Netzwerk administriert, die MAC-Adressen in jedem Switch manuell ein. In der dynamischen Variante lernt der Switch diese Information selbst: Kommt bei einem Switch ein Paket mit einer Absender-MAC-Adresse an, die er noch nicht kennt, trägt er diese Adresse in seiner internen Tabelle mit der Nummer des Ausgangs ein, über die er das Paket empfangen hat.
Üblicherweise enthält die Switching-Tabelle eines Switches also die meiste Zeit über die MAC-Adressen aller Geräte im selben Netzwerksegment. Bei dynamischem Aufbaue der Switching-Tabellen sind die Einträge in der Regel mit einem Ablaufzeitpunkt versehen, der Switch “vergisst” nach einiger Zeit also, wo welches Gerät liegt und muss diese Information neu lernen. So kann auf Änderungen im Netzwerkaufbau reagiert werden.
Address Resolution Protocol
Der Name der ARP-Tabelle, die für jede IP-Adresse im Subnetz die MAC-Adresse des entsprechenden Gerät enthält, leitet sich vom Address Resolution Protocol (engl. für “Adressauflösungsprotokoll”, kurz ARP) ab. Dieses Protokoll erlaubt es jedem Endgerät im Subnetz die MAC-Adressen der anderen Geräte im Subnetz abzufragen.
Beispiel: Angenommen, Gerät A möchte ein Datenpaket an Gerät D mit der IP-Adresse 192.168.1.18 schicken, kennt dessen MAC-Adresse aber nicht. Gerät A schickt nun eine Adressanfrage (ARP Request) an alle anderen Geräte im Subnetz (siehe Lokaler Broadcast). Wenn ein Gerät die MAC-Adresse zur angefragten IP-Adresse kennt, weil sie in seiner lokalen ARP-Tabelle steht, schickt es diese Information als Antwort an Gerät A zurück (ARP Reply). Spätestens Gerät D muss diese Anfrage beantworten können, es können aber auch Antworten von mehreren Geräten zurückkommen.
Sobald Gerät A eine Antwort bekommt, trägt es die nun bekannte MAC-Adresse zur IP-Adresse 192.168.1.18 in seine ARP-Tabelle ein. Weitere folgende Antworten können nun ignoriert werden. Anschließend kann das Paket von Gerät A an D wie oben beschrieben über die Netzzugangsschicht übertragen werden.
Lokaler Broadcast
Um eine Nachricht an alle anderen Geräte im selben Subnetz zu verschicken (“Broadcast”), wird als Ziel-IP-Adresse 255.255.255.255 und als Ziel-MAC-Adresse FF-FF-FF-FF-FF-FF verwendet. Kommt ein Paket mit dieser speziellen, für Broadcasts reservierten Ziel-MAC-Adresse bei einem Switch an, leitet er es an alle Ausgänge weiter (außer natürlich an den Ausgang, über den er das Paket empfangen hat).
Kommunikation zwischen Netzwerken
Dieser Abschnitt befindet sich noch im Aufbau.
Routing
Routing-Protokolle
Distanzvektor-Algorithmus
Breitensuche
4.5 Anwendungsprotokolle
Im Internet gibt es Computer, die Dienste anbieten, genannt Server und Computer, die diese Dienste in Anspruch nehmen, genannt Clients. Beispielsweise bieten die Server von YouTube den Dienst an, auf dort gespeicherte Videos zuzugreifen oder selbst welche hochzuladen. Einige Netzwerkdienste und die von ihnen verwendeten Anwendungsprotokolle wollen wir hier näher betrachten.
World Wide Web
Das World Wide Web (WWW) ist der Teil des Internets, mit dem wohl die meisten vertraut sind und dem wir bereits im Kapitel Informationsdarstellung im Internet begegnet sind: Es besteht aus Websites aus der ganzen Welt, die durch Hyperlinks untereinander verknüpft sind. Websites werden auf weltweit verteilten Webservern vorrätig gehalten (“gehostet”) und können mit Webbrowsern wie Apple Safari, Google Chrome, Microsoft Edge oder Mozilla Firefox abgerufen werden. Übertragen werden sie mit dem Hypertext Transfer Protocol (HTTP).
HTTP
Ein Client und ein Server, die über HTTP miteinander kommunizieren, tauschen Nachrichten aus, die Anfrage (engl. request, vom Client an den Server) und Antwort (engl. response, vom Server an den Client) genannt werden. Dabei behandelt der Server jede Anfrage völlig isoliert, so als hätte der Client noch nie zuvor eine geschickt und würde nie wieder eine schicken. Protokolle, die sich so verhalten, nennt man zustandslos.
Um trotzdem eine Art von Zustand zu simulieren, werden so genannte Cookies verwendet. Cookies sind kleine Textschnipsel, die mit jeder Anfrage und Antwort ausgetauscht und auf dem Client (z. B. im Datenspeicher des Webbrowsers) zwischengespeichert werden. Mittels Cookies kann der Server beispielsweise verschiedene IDs an Clients vergeben, sie so unterscheiden und serverseitig individuelle Informationen für die Clients speichern. Ein Analogon ist etwa eine Auftragsnummer, die man bei der Bestellung erhält, bei der Bezahlung angeben und bei jeder Reklamation bereithalten muss – wobei man sich natürlich auch jedes Mal mit Namen und Adresse identifizieren kann, was den Vorgang aber unnötig verkompliziert.
Anfragen
In HTTP kann der Client u. a. folgende Anfragen stellen
| Anfrage | Erläuterung |
|---|---|
GET |
Dient dazu, eine Ressource vom Server abzufragen. Mit GET können auch Parameter an den Server übertragen werden, die dann in der URL sichtbar werden. GET-Anfragen sollten nicht dazu genutzt werden, Daten zur Speicherung oder Weiterverarbeitung an den Server zu übertragen |
POST |
Dient dazu, Daten zur weiteren Verarbeitung an den Server zu senden. Diese Daten werden nicht in der URL sichtbar, weswegen diese Methode z.B. zum Versand von Login-Daten bevorzugt verwendet werden sollte. POST-Anfragen sollten auch genutzt werden, um Ressourcen auf dem Server zu ändern. |
HEAD |
Dient ebenfalls zum Datenabruf, allerdings wird nicht der Inhalt einer Web-Ressource, sondern nur Metadaten, die sog. Header abgerufen. Damit kann z.B. geprüft werden, ob eine im Cache zwischengespeicherte Seite noch gültig ist. |
PUT |
Dient dazu, eine Ressource auf den Server hochzuladen, wobei die übergebenen Anfragedaten unter der angegebenen URL gespeichert werden. Anders als POST sollen PUT-Anfragen einfach nur Dateien ablegen, statt ggf. komplexere Änderungen anzustoßen. |
PATCH |
Dient dazu, ein bestehendes Dokument zu ändern, ohne es wie bei einer PUT-Anfrage vollständig zu ersetzen. |
DELETE |
Dient dazu, eine Ressource auf dem Server zu löschen |
Die meisten Anfragen sind GET- und POST-Anfragen. Eine Analyse von 2017 ergab, dass rund 77% der HTTP-Anfragen GET- und weitere 20% POST-Anfragen sind. Oft wird POST pauschal für alle Anfragen verwendet, die Daten auf dem Server ändern (also Daten hinzufügen, verändern oder löschen), während GET für rein lesende Anfragen verwendet wird.
Antworten
Jede Antwort eines Webservers beginnt mit einem dreistelligen Statuscode. Die erste Ziffer des Codes gibt dabei Aufschluss über die Art der Antwort:
| Erste Ziffer | Art der Antwort |
|---|---|
| 1__ | Die Anfrage wird bearbeitet, dies wird aber noch einige Zeit dauern |
| 2__ | Die Anfrage wurde erfolgreich bearbeitet. |
| 3__ | Umleitung – die gewünschte Ressource liegt an einem anderen Ort. |
| 4__ | Die Anfrage ist fehlgeschlagen und es liegt (wahrscheinlich) am Client |
| 5__ | Die Anfrage ist fehlgeschlagen und es liegt (wahrscheinlich) am Server |
Die häufigsten Statuscodes sind
| Statuscode | Name | Erläuterung |
|---|---|---|
| 100 | Continue | Signalisiert dem Client, dass eine sehr lange Anfrage noch nicht abgewiesen wurde und der Client mit der Anfrage fortfahren darf. |
| 102 | Processing | Signalisiert dem Client, dass die Anfrage akzeptiert worden ist, aber die Bearbeitung bis zur Antwort noch einige Zeit benötigen wird. Dieser Statuscode wird verwendet, um Timeouts zu vermeiden. |
| 200 | OK | Die Anfrage war erfolgreich und das Ergebnis wird in der Antwort übertragen. |
| 204 | No Content | Die Anfrage war erfolgreich, die Antwort enthält aber bewusst keine Daten. |
| 301/308 | Moved Permanently/Permanent Redirect | Die angefragte Ressource ist dauerhaft an eine neue URL verschoben worden; der Client möge eine neue Anfrage stellen. Link-Shortener-Dienste wie bit.ly oder tinyurl.com reagieren auf Anfragen häufig mit einer 301-Antwort. |
| 302/303/307 | Found/See Other/Temporary Redirect | Die angefragte Ressource ist temporär an eine neue URL verschoben worden. |
| 400 | Bad Request | Die Anfrage war fehlerhaft aufgebaut |
| 401 | Unauthorized | Der Client muss sich für diese Anfrage erst autorisieren. |
| 403 | Forbidden | Der Client hat keine Berechtigung, diese Ressource anzufragen |
| 404 | Not Found | Die angeforderte Ressource konnte nicht gefunden werden, etwa weil in der Adresse ein Tippfehler vorliegt oder ein Link auf eine inzwischen gelöschte Ressource verweist. |
| 408 | Request Timeout | Innerhalb des gegebenen Zeitfensters wurde vom Server keine vollständige Anfrage empfangen. |
| 418 | I’m A Teapot1 | Der Server ist eine Teekanne. |
| 4512 | Unavailable For Legal Reasons | Die gesuchte Ressource ist aus rechtlichen Gründen (z.B. Internetzensur) für den Client nicht verfügbar. |
| 500 | Internal Server Error | Dieser Statuscode wird allgemein bei Serverfehlern zurückgegeben. |
| 502 | Bad Gateway | Der Server hat zur Bearbeitung der Anfrage eine weitere Ressource angefragt, aber keine gültige Antwort erhalten. |
| 503 | Service Unavailable | Der Dienst steht nicht zur Verfügung, z.B. weil der Server überlastet ist. |
Im Webbrowser kann man Anfragen und Antworten sichtbar machen, indem man die Entwicklerwerkzeuge öffnet (was in den meisten Browsern mit der Tastenkombination Umschalt+Strg+I bzw. Command+Option+I möglich ist) und den Reiter “Netzwerk” oder “Netzwerkanalyse” auswählt.
Sobald man dann eine HTTP-Anfrage absendet, etwa indem man eine URL in die Adresszeile eingibt oder einen Link anklickt, werden diese und alle folgenden Anfragen mit den Antworten im Datenfenster aufgelistet.
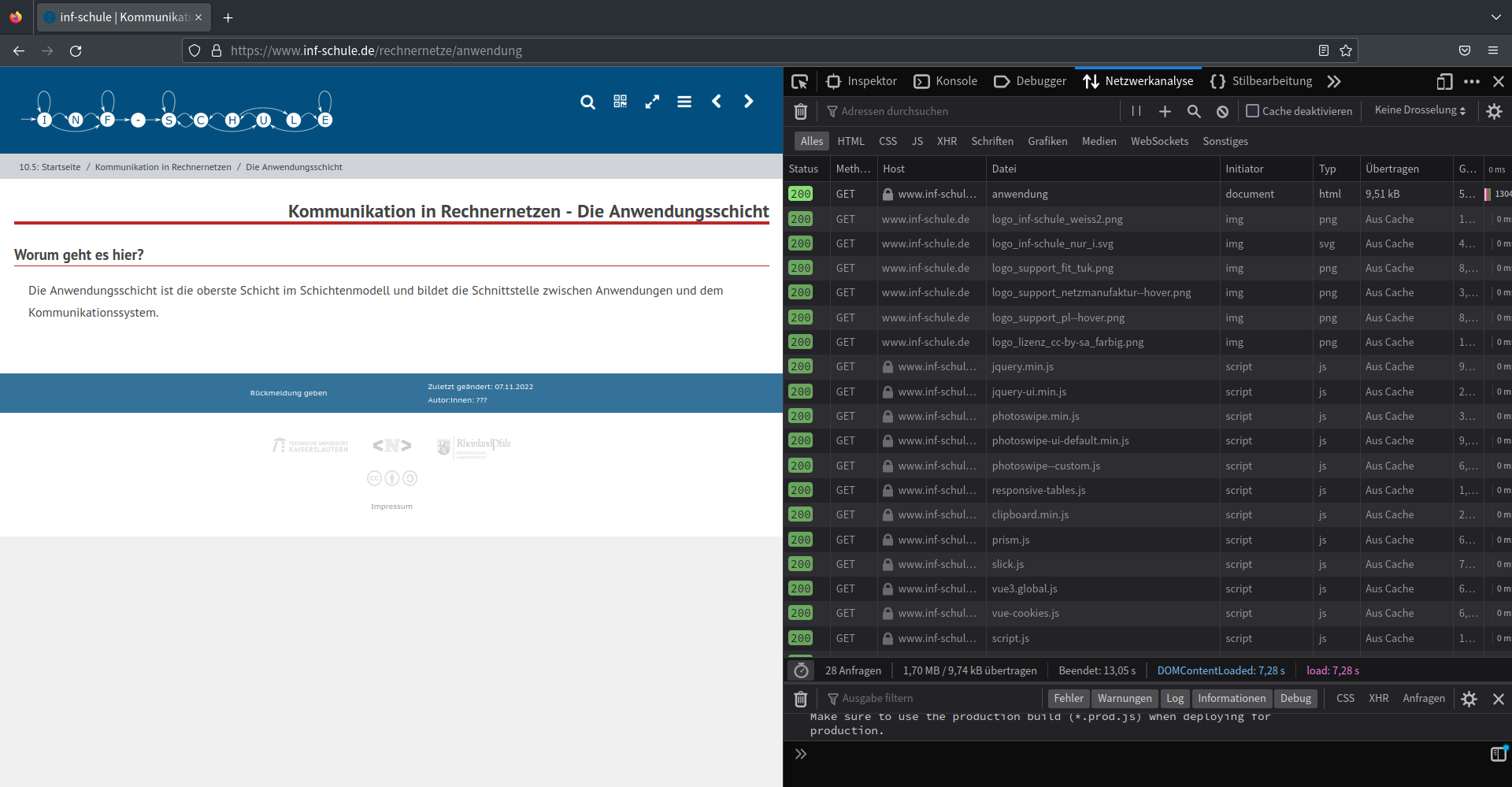
Zu jeder Anfrage können in der Übersicht der Anfragetyp, der Statuscode, Zielrechner, abgefragte Ressource u.v.m. abgelesen werden
Mit einem Klick auf eine Anfrage können noch mehr Details dazu betrachtet werden, z.B. die gesendeten Header von Anfrage und Antwort oder die übertragenen Cookies.
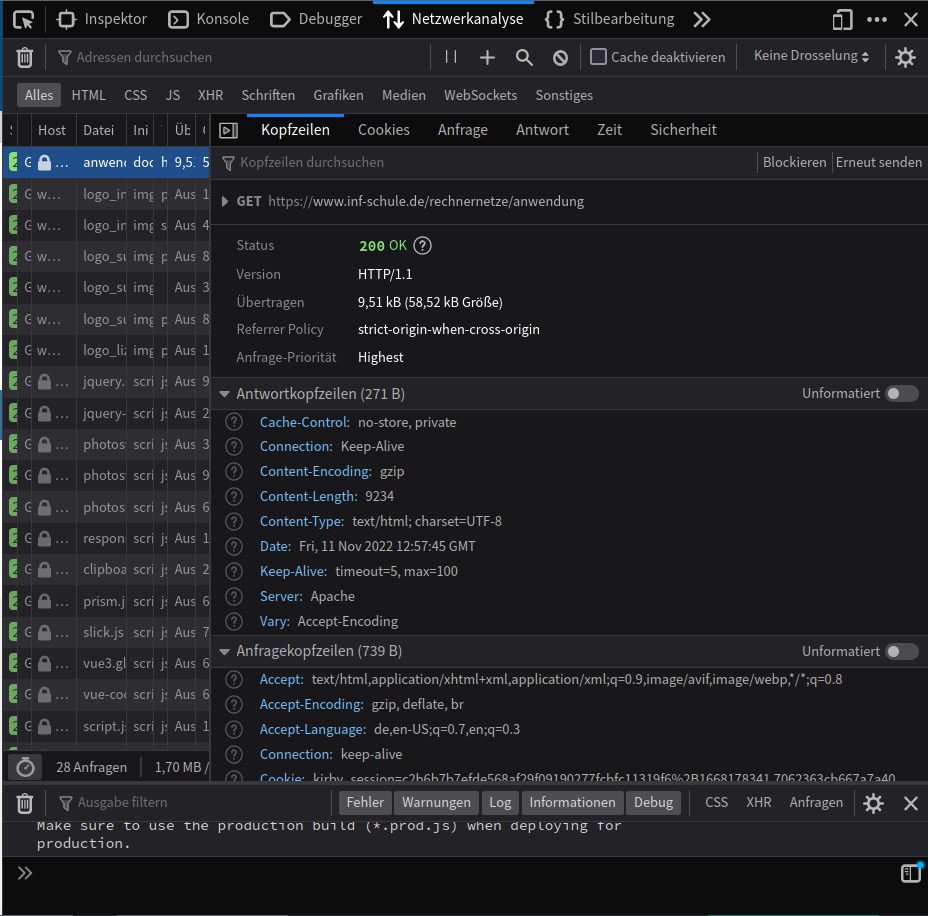
DNS
Das Domain Name System (DNS) sorgt dafür, dass Anfragen, die an Domainnamen wie uni-kiel.de oder iqsh.oncampus.de gerichtet sind, auch beim richtigen Rechner ankommen, z. B. verbirgt sich hinter dem Domainnamen uni-kiel.de der Webserver mit der IP-Adresse 134.245.13.22. Diesen Prozess bezeichnet man als Namensauflösung. Die dafür notwendigen Daten, die Resource Records sind weltweit auf vielen sogenannten Nameservern verteilt gespeichert.
Domain-Namen
Die Domainnamen sind rückwärts zu lesen und die dazugehörigen Informationen sind in einer Baumstruktur organisiert:
Der Domainname iqsh.oncampus.de ist folgendermaßen zu lesen: de ist die Top-Level-Domain (TLD) und gibt an, dass die Domain in Deutschland registriert ist. Andere Top-Level-Domains sind etwa at für Österreich, sh für St. Helena oder edu für Bildungseinrichtungen. oncampus ist die Domain und gibt an, dass diese Webseite auf einem Computer des E-Learning-Anbieters oncampus liegt. iqsh ist eine Subdomain und identifiziert genau denjenigen unter den Computern von oncampus, auf dem die Seite liegt. Subdomains sind ebenfalls hierarchisch organisiert und schlüsseln die Organisation der Server genauer auf. Beispielsweise ist die Webanwendung GitLab der Arbeitsgruppe Zuverlässige Systeme am Institut für Informatik der Uni Kiel über die Domain git.zs.informatik.uni-kiel.de erreichbar. Eine so zusammengesetzte Namensangabe wird als Fully Qualified Domain Name (FQDN) bezeichnet.
Resource Records
Zu einem Domainnamen können die verschiedensten Informationen bei einem DNS-Server hinterlegt sein. Diese Informationen werden in so genannten Resource Records gespeichert, die jeweils einen bestimmten Typ haben und dort öffentlich zugänglich sind. Einige dieser Typen sind:
| Typ | Information |
|---|---|
A |
Gibt die IPv4-Adresse zu einer Domain an |
AAAA |
Gibt die IPv6-Adresse zu einer Domain an |
CNAME |
Gibt den eigentlichen Domainnamen an, der sich hinter einer Alias-Domain verbirgt. |
MX |
Gibt den Mailserver an, der für eine bestimmte Domain zuständig ist |
NS |
Gibt den Nameserver an, der für die Subdomains einer Domain zuständig ist |
SOA |
Gibt den Start of Authority an, d.h. die Stelle, die alle Informationen zu einer Domain ursprünglich verwaltet. |
SRV |
Gibt an, welche IP-basierten Dienste innerhalb einer Domain angeboten werden. |
TXT |
Kann beliebige Informationen zur Domain in Textform speichern |
Mit Kommandozeilenwerkzeugen wie nslookup (für Windows) oder dig/dog (für Linux) können diese Resource Records abgefragt werden.
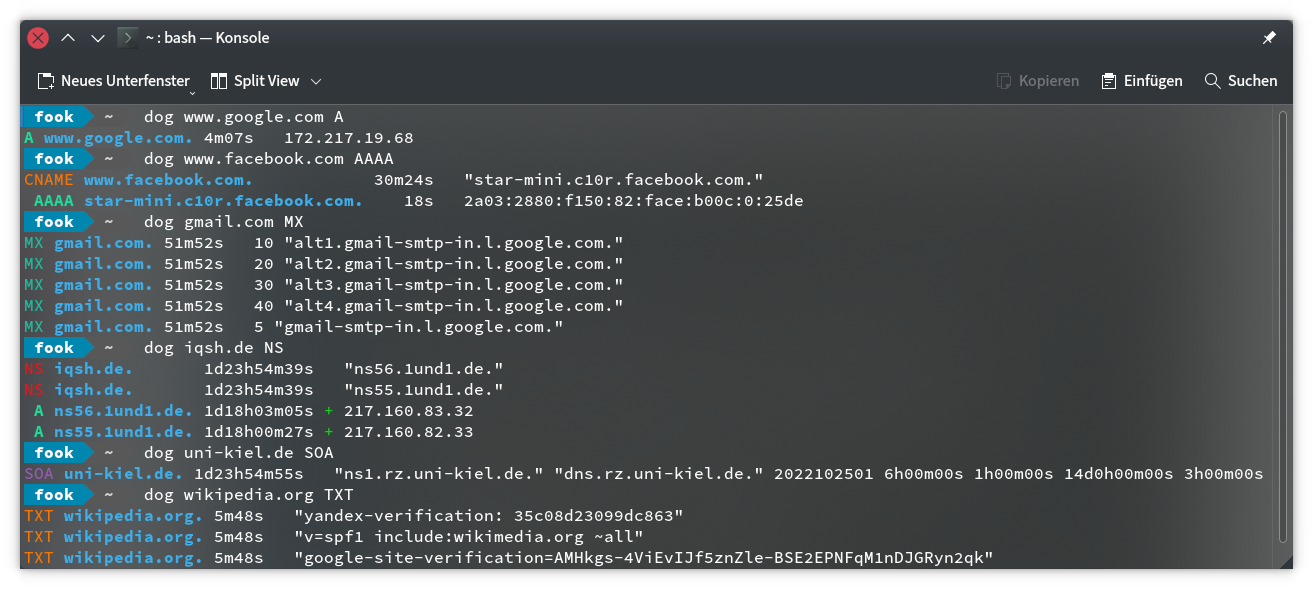
DNS-Abfragen
Jede Anfrage an einen Domainnamen muss zuerst in eine IP-Adresse übersetzt werden. Diese Anfrage geht theoretisch zunächst an einen der 13 weltweit verteilten Root-Nameserver, welche die Adressauflösung an der Wurzel des Adressbaums erledigen und in der Regel nur eine Liste der DNS-Server zurückliefern, die für die nächsttiefere Domain zuständig sind (die sogenannten autoritativen Nameserver) und die Anfrage dann weiterverarbeiten.
Wenn ein DNS-Server die Informationen zur angefragten Domain vorrätig hält, wird die gesuchte IP-Adresse direkt zurückgegeben, ansonsten wird die Anfrage entweder iterativ oder rekursiv weitergeleitet.
Iterative Namensauflösung
Iterative Namensauflösung bedeutet, dass der DNS-Server an den Client eine Liste von anderen DNS-Servern weiterleitet, die Genaueres zur gesuchten Domain wissen könnten.
Eine iterative Namensauflösung für die Adresse iqsh.oncampus.de könnte etwa so ablaufen:
de 172800 NS IN f.nic.de,
de 172800 NS IN l.de.net,
de 172800 NS IN n.de.net,
de 172800 NS IN s.de.net,
de 172800 NS IN z.nic.de note over A, B: Root-Server liefert eine Liste der DNS-Server,
die für .de zuständig sind A->>+C: iqsh.oncampus.de IN A note over A, C: Client fordert IP-Adresse (A) von einem dieser Server,
hier z.nic.de C->>-A: oncampus.de 86400 NS IN dns-1.dfn.de,
oncampus.de 86400 NS IN dns-3.dfn.de,
oncampus.de 86400 NS IN dns.fh-luebeck.de note over A, C: z.nic.de liefert eine Liste der DNS-Server,
die für .oncampus.de zuständig sind. A->>+D: iqsh.oncampus.de IN A note over A, D: Client fordert IP-Adresse (A) von dns-3.dfn.de D->>-A: iqsh.oncampus.de 86400 A IN 193.175.122.162 note over A, D: dns-3.dfn.de liefert die IP-Adresse von iqsh.oncampus.de an den Client
Rekursive Namensauflösung
Rekursive Namensauflösung bedeutet, dass der DNS-Server die Anfrage an einen anderen DNS-Server weiterleitet, wartet, bis er von diesem ein Ergebnis bekommt (das wiederum rekursiv weitergeleitet worden sein könnte) und dieses an den Client zurückliefert.
Eine rekursive Namensauflösung für die Adresse iqsh.oncampus.de könnte etwa so ablaufen:
an einen DNS-Server, der für die Domain
.de zuständig ist, hier z.nic.de. C->>+D: iqsh.oncampus.de IN A note over C, D: z.nic.de leitet die Anfrage weiter
an einen DNS-Server, der für die Domain
.oncampus.de zuständig ist, hier dns-3.dfn.de D->>-C: iqsh.oncampus.de
86400 A IN 193.175.122.162 note over C, D: dns-3.dfn.de liefert die IP-Adresse
von iqsh.oncampus.de an z.nic.de C->>-B: iqsh.oncampus.de
86400 A IN 193.175.122.162 note over B, C: z.nic.de liefert die IP-Adresse
von iqsh.oncampus.de an den Root-Server B->>-A: iqsh.oncampus.de
86400 A IN 193.175.122.162 note over A, B: Root-Server liefert die IP-Adresse an den Client
Der Nachteil von rekursiver Namensauflösung ist, dass die Server am Anfang dieser Abfragekette – vor allem also die Root-Server – die Anfragen über einen längeren Zeitraum zwischenspeichern und die Antworten der anderen Nameserver abwarten müssen.
Vorteile der rekursiven Namensauflösung sind, dass die DNS-Client-Software simpler gehalten werden kann und dass alle DNS-Server auf dem Weg der Abfrage die IP-Adresse ebenfalls erhalten und gegebenenfalls für folgende DNS-Abfragen zwischenspeichern können.
DNS-Protokoll
DNS bezeichnet desweiteren auch das Anwendungsprotokoll, das beschreibt, wie ein Client mit einem DNS-Server kommuniziert, um die IP-Adresse zu einem Domainnamen zu ermitteln. Die Kommunikation besteht aus Anfragen (DNS Query) und Antworten (DNS Reply).
- Eine DNS Query beinhaltet einen oder mehrere Domainnamen, deren IP-Adressen ermittelt werden sollen. Daneben werden in der Nachricht Optionen angegeben, z. B. ob eine rekursive Namensauflösung gewünscht ist oder nicht.
- Eine DNS Reply beinhaltet die Anfragen und Antworten für jede Anfrage, in denen u. a. die ermittelten IP-Adressen der Domainnamen angegeben sind (oder die IP-Adressen der nächsten verantwortlichen DNS-Server, wenn der Name noch nicht vollständig aufgelöst wurde).
Zur Übertragung von DNS-Nachrichten über die Transportschicht werden sowohl TCP als auch UDP auf dem Standardport 53 genutzt.
DHCP
Das Dynamic Host Configuration Protocol DHCP dient dazu, Computern, die einem Netzwerk neu beitreten, automatisch eine IP-Adresse zuzuweisen. Das geschieht zum Beispiel (in der Regel), wenn man sich im heimischen WLAN einloggt oder auf dem Handy die mobile Datennutzung aktiviert. Damit dies gelingt, muss im lokalen Netzwerk ein DHCP-Server aktiviert sein, in heimischen Netzwerken ist dies überwiegend Teil des Funktionsumfangs des WLAN-Routers.
Da der suchende Computer weder eine eigene IP-Adresse hat noch die des DHCP-Servers kennt, werden alle Anfragen und Antworten an die Broadcast-Adresse 255.255.255.255 gesende. Das bedeutet, dass diese Datenpakete bei allen Rechnern im lokalen Netz ankommen. In jeder Anfrage und jeder Antwort wird die MAC-Adresse des suchenden Rechners mitgeschickt; dadurch kann dieser Rechner erkennen, welche Nachrichten an ihn gesendet sind.
Die Zuweisung einer IP-Adresse durch DHCP verläuft regelhaft in fünf Schritten:
DHCPDISCOVER. Der Client sendet eineDHCPDISCOVER-Anfrage mit seiner MAC-Adresse an die Broadcast-IP-Adresse 255.255.255.255. Als Absenderadresse gibt der Client die Netzwerk-Adresse 0.0.0.0 an.DHCPOFFER. Der DHCP-Server reagiert auf die Anfrage und bietet dem Client eine IP-Adresse aus seinem Adressbereich an. Zusätzlich übermittelt der DHCP-Server noch weitere Informationen wie die verwendete Subnetzmaske, die IP-Adresse des Standardgateways oder des zu verwendenden DNS-Servers. Da der Client noch keine IP-Adresse hat, wird auch dieses Angebot an die 255.255.255.255 geschickt.ARP REQUEST. Um sicherzugehen, dass die angebotene IP-Adresse nicht schon anderweitig vergeben ist (vielleicht hat ein anderer Nutzer seinen Computer händisch konfiguriert?), schickt der Client einenARP REQUESTan alle Geräte.- Nun gibt es zwei Möglichkeiten:
DGHCPDECLINE, falls derARP REQUESTbeantwortet wird, denn dann ist die angebotene IP-Adresse schon vergeben. In diesem Fall schickt der Client einenDHCPDECLINEan den Server und beginnt das ganze Prozedere von Schritt 1. Der Server merkt sich, dass diese IP-Adresse schon belegt ist, und wird diese in Zukunft nicht mehr anbieten.DHCPREQUEST, falls derARP REQUESTungehört verhallt, denn dann ist die angebotene IP-Adresse noch frei. Der Client schick nun einenDHCPREQUESTund bittet den DHCP-Server darum, die angebotene IP-Adresse nutzen zu dürfen.
- Der Server kann darauf auf zweierlei Arten reagieren:
DHCPACKbestätigt die Anfrage, der Client übernimmt die IP-Adresse.DHCPNAKlehnt die Anfrage ab, der Client muss den ganzen Prozess von vorn mit einemDHCPDISCOVERbeginnen.
Zur Übertragung von DHCP-Nachrichten über die Transportschicht wird UDP auf den Ports 67 (für den Server) und 68 (für den Client) genutzt.
Mailprotokolle
Für den Versand und Abruf von E-Mails kommen drei Protokolle zum Einsatz:
- das Post Office Protocol, das in Version 3 (POP3) zum Abruf von E-Mails verwendet wird
- das Interactive Mail Access Protocol (IMAP), das ebenfalls dem E-Mail-Abruf dient
- das Simple Mail Transfer Protocol (SMTP) zum Versand von E-Mails
POP3
POP3 ist ein einfaches Protokoll zum Abruf von E-Mails von Mail-Servern. Typischerweise lauscht POP3 auf dem TCP-Port 110. Da POP3 normalerweise keine verschlüsselte Datenübertragung vorsieht, gibt es auch die SSL-verschlüsselte Variante POP3S, die auf Port 995 lauscht.
Es gibt aber auch Erweiterungen für POP3, um das Passwort oder die gesamte Kommunikation verschlüsselt zu übertragen. B->>A: +OK Passwort passt. A->>B: STAT note over A, B: Client fragt mit STAT ab, wie viele ungelesene Nachrichten vorliegen B->>A: +OK 2 892 note over A, B: lies 2 ungelesene Nachrichten, die zusammen 892 Byte lang sind A->>B: LIST B->>A: +OK 2 ungelesene Nachrichten (892 Byte)
1 196
2 696
. note over A, B: die einzelnen Mails werden durchnummeriert aufgezählt, ihre Größe wird dabei mit angegeben.
Längere Antworten des Servers werden mit einem Punkt in einer Extrazeile beendet. A->>B: RETR 1 note over A, B: Client ruft E-Mail Nr. 1 ab B->>A: +OK Hier ist Mail Nr. 1
From: erika.mustermann@mustermail.de
To: max.mustermann@mustermail.de
... A->>B: RETR 2 B->>A: +OK Hier ist Mail Nr. 2... A->>B: DELE 1 B->>A: +OK Mail 1 zum Löschen markiert note over A, B: Es gibt keine Möglichkeit in POP3, gelesene E-Mails auf dem Server zu hinterlassen.
Entweder lädt man sich die Mail herunter und löscht die Kopie auf dem Server
oder die Kopie auf dem Server bleibt ungelöscht und wird bei jedem folgenden E-Mail-Abruf als ungelesen angezeigt. A->>B: DELE 2 B->>A: +OK Mail 2 zum Löschen markiert A->>B: QUIT note over A, B: Gelesene Mails werden nur gelöscht, wenn die Verbindung sauber mit QUIT beendet wird. B->>A: +OK Auf Wiedersehen
Gegenüber IMAP, das ebenfalls zum Mail-Abruf genutzt wird, bietet POP3 den Nachteil, dass es nur ein Postfach für eingehende E-Mails gibt und diese nach dem Abruf vom Server gelöscht werden müssen. Mehrere E-Mail-Clients zu synchronisieren, wird dadurch enorm erschwert.
IMAP
Im Gegensatz zum POP, an dem die Entwicklung zum Erliegen gekommen ist, hat sich IMAP als Standard zum E-Mail-Abruf etabliert. IMAP ermöglicht es, E-Mails auf dem Server in Ordnern zu sortieren und mittels Flags zusätzliche Informationen zu einer E-Mail zu speichern.
| Flag | Information |
|---|---|
\Seen |
E-Mail wurde gelesen |
\Answered |
E-Mail wurde beantwortet |
\Flagged |
E-Mail wurde als dringend markiert |
\Deleted |
E-Mail wurde zum Löschen vorgemerkt |
\Draft |
E-Mail ist noch im Entwurfsstadium |
Diese Flags erleichtern es enorm, E-Mails über mehrere Geräte abzurufen, weil die Mails auf dem Server verbleiben können und durch die Flags auf allen Clients angezeigt werden kann, ob die Mails bereits gelesen und bearbeitet worden sind.
Die Kommunikation verläuft vom Herstellen bis zum Schließen in mehreren Zuständen:
IMAP hat hierbei drei Möglichkeiten, auf einen Verbindungsaufbau zu reagieren:
OKist der Standardfall; dann muss der Nutzer sich zunächst auf irgendeine Art und Weise authentifizieren- Eine
PREAUTH-Begrüßung ist in Situationen sinnvoll, wenn der Nutzer sich bereits anderweitig authentifiziert hat; dann kann dieser Schritt entfallen - Wenn der Client sich aus welchem Grund auch immer nicht mit dem Server verbinden soll, kann dieser die Verbindung mit einer
BYE-“Begrüßung” von vornherein ablehnen.
SMTP
SMTP dient anders als POP und IMAP dem Versand von E-Mails und lauscht auf dem Port 25. Praktisch kann SMTP an vielen Schulen ausprobiert werden, da die Schulverwaltungssoftware IServ einen unverschlüsselten SMTP-Server zur Verfügung stellt, der zumindest eingehende E-Mails zu autorisierten Accounts akzeptiert.
Der Versand einer E-Mail mit SMTP läuft folgendermaßen ab:
beende diese mit einem . auf einer Extra-Zeile. note over A, B: Die Daten der E-Mail können sehr umfangreich sein,
sodass es für den Client Sinn ergibt, diese in mehreren Anfragen abzusenden.
Der Server akzeptiert schweigend alle Nachrichten des Clients,
bis ihm ein einzelner Punkt in einer Zeile gesendet wird.
Dies ist das Signal für das Ende der Nachricht. A->>+B: From: Max Mustermann A->>B: To: Erika Gabler A->>B: Subject: Urkunden sind abgeschickt! A->>B: Erika, mein Mausepups! A->>B: Ich habe unsere Geburtsurkunden ans Standesamt geschickt! A->>B: Unserer Hochzeit steht nichts mehr im Wege! A->>B: Bald bist du auch eine Mustermann! A->>B: In Liebe, A->>B: Dein Maxibär A->>B: . note over A, B: Dieser . signalisiert dem Server das Ende der Nachricht, deswegen sendet er eine bestätigende Antwort. B->>-A: 250 Die Mail wird versendet A->>B: QUIT B->>A: 221 Auf Wiedersehen
In SMTP ist eine Authentifizierung und Autorisierung des Nutzers standardmäßig nicht vorgesehen. Deswegen bergen öffentlich zugängliche unverschlüsselte SMTP-Server ein enorm hohes Risiko für Missbrauch und Spam. Die meisten SMTP-Server sind darum nur durch verschlüsselte Schichten erreichbar, die eine Authentifizierung mit TLS erzwingen.
-
Dieser Statuscode stammt aus der scherzhaften HTTP-Erweiterung HTCPCP (Hyper Text Coffee Pot Control Protocol), das der Steuerung von Kaffeemaschinen dienen soll. Siehe RFC 2324: Hyper Text Coffee Pot Protocol (HTCPCP) ↩︎
-
Der Statusode 451 ist eine Anspielung auf den dystopischen Roman “Fahrenheit 451” von Ray Bradbury. ↩︎
5. Programmierung in Python
5.1 Programmierung in Python
Die Sprache Python
Nachdem wir mit der visuellen Programmiersprache Scratch die wichtigsten Grundlagen der Programmierung in einer lernendengerechten Aufbereitung kennengelernt haben, wollen wir diese Kenntnisse nun mit einer textuellen Programmiersprache vertiefen. Wir werden hierfür die Programmiersprache Python und die Entwicklungsumgebung Thonny verwenden.
Sowohl Python als auch Thonny wurden ursprünglich für den Einsatz in schulischen Kontexten entwickelt. Dennoch ist Python eine vollwertige Programmiersprache, die z. B. unter der Haube von Anwendungen wie Facebook, Dropbox oder Spotify steckt. Python zeichnet sich durch eine kompakte, gut lesbare Syntax aus, die mit wenigen eingebauten Schlüsselwörtern auskommt und durch eine große Vielzahl von Bibliotheken ergänzt wird.
Mit einigen elementaren Programmierkenntnissen lassen sich in Python recht schnell funktionierende Anwendungen auf die Beine stellen. Dadurch eignet sich Python gut, um in kurzer Zeit Prototypen oder kleine Skripte für einfache Berechnungen zu programmieren.
Python gehört zur Familie der interpretierten Programmiersprachen, was bedeutet, dass der menschengeschriebene Programmtext direkt von einem Interpreter genannten Programm ausgeführt wird. Dadurch müssen Programme nicht erst in eine maschinenlesbare Form übersetzt werden, was das Entwickeln und Testen vereinfacht, aber auf der anderen Seite auch verhindert, dass bestimmte Programmierfehler vor der Ausführung entdeckt werden.
Die Entwicklungsumgebung Thonny
Software-Entwicklung hat viele Facetten: Der Code muss geschrieben, verwaltet und getestet werden. Für all das lassen sich unterschiedliche Programme benutzen: Wir können den Code mit einem einfachen Texteditor schreiben, mit dem Explorer in Ordnern organisieren und mit der Kommandozeile testen, oder wir können eine integrierte Entwicklungsumgebung (engl. integrated development environment, kurz IDE) einsetzen, die all diese Funktionalitäten in einer einzigen Anwendung bündelt.
Eine Art von IDE haben wir bereits kennen gelernt, nämlich Scratch, das auf einer Seite Ansichten zum Programmieren, zur Verwaltung von Grafiken und Soundeffekten, sowie auf der anderen Seite zum Ausführen und Testen des Programms bereithält.
Für Python steht eine Vielzahl von Entwicklungsumgebungen zur Verfügung, wie etwa PyCharm, Visual Studio Code, PyDev, IDLE usw.
Wir werden eine besonders lernendenfreundliche Entwicklungsumgebung benutzen, die speziell für den Einsatz als Lernhilfsmittel und nicht für die Verwendung in großen, komplexen Programmierprojekten konzipiert wurde: Thonny.1
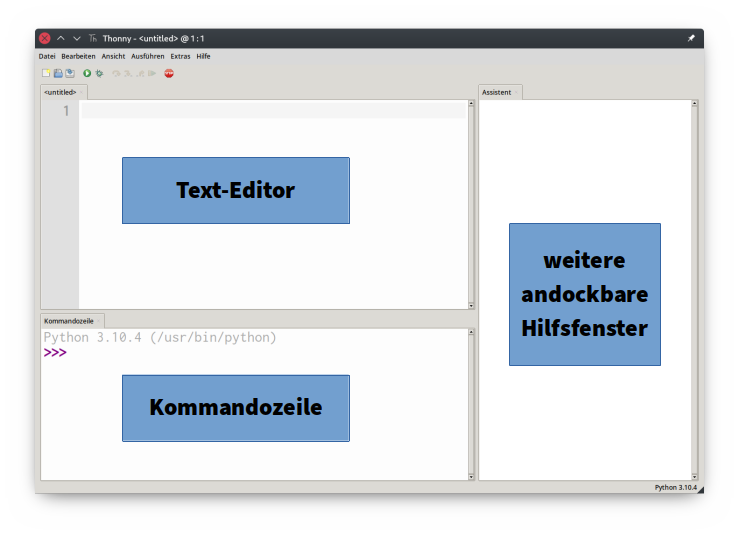
Thonny ist eine einfache IDE, die zwar Anwendungsbestandteile zum Schreiben, Testen, Analysieren und zur Fehlerkorrektur von Programmen enthält, die aber mit relativ wenig Aufwand in Betrieb zu nehmen ist und die keine besonderen Vorkenntnisse in der Organisation von größeren Codemengen erfordert. Außerdem beinhaltet Thonny bereits den Python-Interpreter (Python muss also nicht extra installiert werden), sowie eine einfache Paket-Verwaltung.2
Die Benutzeroberfläche von Thonny ist modular aufgebaut. Im Anwendungsfenster lassen sich u. a. die folgenden Bereiche anzeigen:
- Links oben befindet sich der Text-Editor. In diesem Unterfenster schreiben wir unsere Python-Programme. Es können mehrere Python-Dateien gleichzeitig in mehreren Tabs geöffnet werden.
- Links unten befindet sich das Konsolenfenster mit der Kommandozeile. Wenn wir ein Python-Programm ablaufen lassen, werden hier Ein- und Ausgaben sowie Fehlermeldungen angezeigt. Wenn nicht gerade ein Programm abläuft, steht uns die Kommandozeile als interaktive Konsole zur Verfügung, in der wir Python-Anweisungen eingeben können, die dann sofort ausgeführt werden. Nach Beendigung eines Programmablaufs können wir über die Konsole auf sämtliche Variablen und Funktionen dieses Programms zugreifen.
- Der Assistent zeigt (wenn ein Fehler auftritt) ausführlichere Fehlermeldungen an und macht teilweise Verbesserungsvorschläge für unseren Code.
- Eine Auflistung aller im aktuellen Programm verwendeten Variablen und ihrer aktuellen Werte
- Eine Ansicht, mit der wir durch die Dateien des Projekts bzw. des aktuell geöffneten Ordners navigieren können
- Eine Notizen-Ansicht, um Ideen und Gedanken festzuhalten
- Eine Ansicht der Hilfe-Seiten für Thonny (auf englisch)
Beim Programmstart von Thonny werden der Text-Editor und die Kommandozeile standardmäßig angezeigt. Alle weiteren Bereiche können über den Menüpunkt “Ansicht” an- oder ausgeschaltet werden.
-
Die Installationsdateien für Thonny für verschiedene Betriebssysteme können von der offiziellen Website https://thonny.org heruntergeladen laden. Dort finden sich auch kurze Installationsanleitungen. ↩︎
-
Ein Python-“Paket” oder Modul beinhaltet Zusatzfunktionen für Python z. B. zur Bildverarbeitung oder zur Spieleentwicklung. ↩︎
5.2 Einstieg in Python
Python wurde mit dem Ziel entwickelt, besonders gut lesbar zu sein und besonders kompakten Code zu produzieren. Die hohe Lesbarkeit wird unter anderem dadurch erreicht, dass für einige Operatoren, die in anderen Programmiersprachen durch Symbole ausgedrückt werden, in Python englische Wörter verwendet werden. Ein Beispiel dafür sind die logischen Operatoren, mit denen zwei Aussagen verknüpft werden können. In C heißen diese z.B. !, && und ||, in Python dagegen not, and und or.
Einrückungen
Um die Lesbarkeit von Programmen zu erhöhen, ist es üblich, den Quellcode durch Zeilenumbrüche und Einrückungen zu strukturieren. In Python ist dies nicht nur üblich (und damit dem Geschmack und der Disziplin der Programmiererin unterworfen), sondern explizit vorgeschrieben: bestimmte Strukturelemente, die in anderen Programmiersprachen durch Klammern oder Schlüsselwörter vorgegeben sind, werden in Python durch Einrückung gesteuert. Durch diese Festlegung soll der Quellcode automatisch besser lesbar werden, da durch die Einrückungstiefe intuitiv erfasst werden kann, welche Codezeile zu welchem Kontrollblock gehört.
5.3 Variablen und Ausdrücke
Variablen
Das Konzept der Variablen ist uns bereits aus der visuellen Programmierung vertraut (siehe Abschnitt Programmieren mit Variablen). Kurz zusammengefasst, ist eine Variable ein Bezeichner, der eine Referenz, also einen Verweis auf eine Stelle im Objektspeicher von Python enthält. Im Objektspeicher sind Objekte wie die Zahl 42, der Text “Hallo Welt” oder eine Liste mit den Elementen 1, 2 und 3 abgelegt.
Definition und Zuweisung
Anders als in Scratch oder vielen anderen Programmiersprachen müssen Variablen in Python vor der Verwendung nicht definiert werden. Man weist ihnen einfach einen Wert zu, etwa:
nettobetrag = 16.80
und kann den Wert dieser Variablen anschließend für weitere Berechnungen verwenden:
bruttobetrag = nettobetrag * 1.19
Die Syntax ist hier: Bezeichner = Ausdruck, wobei der Bezeichner mit einem Buchstaben beginnen muss (bei Variablen üblicherweise ein Kleinbuchstabe) und hinter dem Gleichheitszeichen jeder beliebige Ausdruck stehen darf, der ein Ergebnis zurückliefert. Beispiele:
adresse = 'Musterstr. 1, 12345 Musterstadt'hoechstpunktzahl = 42c = math.sqrt(a**2 + b**2)name = input('Bitte gib deinen Vornamen an')
Wie schon bei der visuellen Programmierung erwähnt, sollte der Bezeichner dabei möglichst aussagekräftig gewählt werden. Generische Variablenbezeichner wie “x” oder “variable” sollten möglichst vermieden werden.
Dass Variablen vor der Verwendung nicht definiert werden müssen, birgt das Risiko von Laufzeitfehlern, wenn man sich vertippt. Betrachten wir die folgenden Codebeispiele:
groesse = input('Bitte geben Sie Ihre Größe in cm ein! ')
groesse = groesse / 100
print('Sie sind ' + str(groesse) + ' m groß.')
und
groesse = input('Bitte geben Sie Ihre Größe in cm ein! ')
greosse = groesse / 100
print('Sie sind ' + str(groesse) + ' m groß.')
Wird das erste Programm gestartet, so erhalten wir die folgende Ausgabe im Konsolenfenster:
Bitte geben Sie Ihre Größe in cm ein! 203
Sie sind 2.03 m groß.
Zur Erklärung: Das Programm pausiert nach der ersten Ausgabe (“Bitte geben Sie Ihre Größe in cm ein!”) und wartet, bis wir eine Eingabe in die Konsole eingeben und mit der Eingabetaste bestätigen. In diesem Fall haben wir die Zahl 203 eingegeben.
Wird anschließend das zweite Programm ausgeführt, erzeugt es die folgende Ausgabe in der Konsolenfenster (auch hier geben wir wieder 203 ein):
Bitte geben Sie Ihre Größe in cm ein! 203
Sie sind 203 m groß.
Was ist passiert? Das zweite Programm enthält in Zeile 2 einen Tippfehler: Statt groesse steht dort greosse. Der Python-Interpreter legt darum eine neue Variable namens greosse an und speichert darin den Wert 2.03. Der Wert von groesse bleibt unverändert.
Datentypen
Nicht mit allen Arten von Daten lassen sich die gleichen Operationen durchführen. Betrachten wir als Beispiel den Operator *:
>>> 6 * 7
42
>>> 4 * 3.141592653587
12.566370614348
>>> 'kartoffel' * 'salat'
Traceback (most recent call last):
File "<pyshell>", line 1, in <module>
TypeError: can't multiply sequence by non-int of type 'str'
>>> 2 * 'moin '
'moin moin '
>>> 2.5 * 'moin'
Traceback (most recent call last):
File "<pyshell>", line 1, in <module>
TypeError: can't multiply sequence by non-int of type 'float'
>>> 4 * [1,2,3]
[1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3]
Mit dem *-Operator können Zahlen multipliziert und Zeichenketten vervielfältigt werden. Hier gibt es Unterschiede bezüglich der Datentypen der Operanden (d. h. der Werte bzw. Ausdrücke, die links und rechts des Operators stehen).
Die wichtigsten elementaren Datentypen in Python sind:
| Typ | Erklärung | Beispiele |
|---|---|---|
int |
für ganze Zahlen (engl. integer numbers) | 0, 42, 3190701205 |
float |
für Dezimalzahlen (“Kommazahlen”, engl. floating-point numbers) | 0.5, 42.0, 3.141592 |
str |
für beliebige Zeichenketten (engl. strings) | 'Hello World', '42', 'https://iqsh.landsh.de' |
bool |
für Wahrheitswerte (engl. boolean)1 | True, False |
Konvertierung von Datentypen
Mit den Funktionen int, float, str und bool können Objekte in andere Datentypen umgewandelt (“konvertiert”) werden. Das wird als Type Casting bezeichnet (auf deutsch “Datentypumwandlung” oder kurz “Konvertierung”). Dabei können Daten verloren gehen, und es sind nicht alle Konvertierungen möglich. Zum Beispiel gehen bei der Konvertierung int(25.95) zwangsläufig die Nachkommastellen verloren, das Ergebnis ist die Ganzzahl 25.2
Die folgende Tabelle zeigt anhand von Beispielen, welche Konvertierungen zwischen den vier elementaren Datentypen möglich sind und welche Ergebnisse wir erhalten:
| Argumentwert | int(x) |
float(x) |
str(x) |
bool(x) |
|---|---|---|---|---|
x = 2 |
2 |
2.0 |
'2' |
True |
x = 2.7818 |
2 |
2.7818 |
'2.7818' |
True |
x = 'zwei' |
Fehler | Fehler | 'zwei' |
True |
x = True |
1 |
1.0 |
'True' |
True |
Hinweis: Die Konvertierung von Zahlen oder Strings in Wahrheitswerte mit bool ergibt immer True, außer für die Werte 0, 0.0 und den leeren String ''.
Operatoren
Mathematische Operatoren
Mathematische Operatoren werden für Berechnungen mit numerischen Werten (Datentypen int und float) verwendet.
Die Operanden (hier x und y genannt) sind numerische Werte oder Ausdrücke, die numerische Werte ergeben. Die Berechnungsergebnisse sind ebenfalls numerische Werte.
| Operator | Bezeichnung | Beschreibung | in Scratch |
|---|---|---|---|
x + y |
Addition |  |
|
x - y |
Subtraktion |  |
|
x * y |
Multiplikation |  |
|
x / y |
Division | Liefert immer einen Wert vom Datentyp float als Ergebnis zurück, auch wenn das Ergebnis ganzzahlig ist. Beispiel: 4 / 2 → 2.0 |
 |
x // y |
Ganzzahlige Division | Liefert immer einen Wert vom Datentyp int zurück, ggf. wird das Ergebnis also konvertiert. Beispiel: x // y ergibt dasselbe wie int(x / y) |
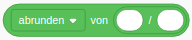 |
x % y |
Modulo | Berechnet den Rest, der bei der ganzzahligen Division von x durch y übrigbleibt. Beispiel: 10 % 3 → 1 |
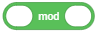 |
x ** y |
Potenz | Berechnet xy (“x hoch y”), also die y-fache Multiplikation von x. | siehe unten3 |
Vergleichsoperatoren
Mit Vergleichsoperatoren können zwei Werte oder die Ergebnisse zweier Ausdrücke verglichen werden. Das Ergebnis ist ein Wahrheitswert True oder False (Ausdrücke mit einem Vergleichsoperatoren sind also logische Ausdrücke).
Die Operanden können dabei verschiedene Datentypen haben, so lassen sich numerische Werte, Zeichenketten und auch andere Objekte miteinander vergleichen. In den folgenden Beispielen stehen x und y also für Werte beliebiger Datentypen (z. B. int, float oder str).
| Operator | Bezeichnung | Hinweis | in Scratch |
|---|---|---|---|
x == y |
Gleichheit | Achtung: In Python wird ein doppeltes Gleichheitszeichen zur Überprüfung der Gleichheit verwendet. Ein einfaches Gleichheitszeichen beschreibt dagegen eine Variablenzuweisung! |  |
x != y |
Ungleichheit |  |
|
x < y |
Echt kleiner |  |
|
x <= y |
Kleiner oder gleich |  |
|
x > y |
Echt größer |  |
|
x >= y |
Größer oder gleich |  |
Logische Operatoren
Logische Operatoren werden für Berechnungen mit Wahrheitswerten (Datentyp bool) verwendet, z. B. um mehrere Wahrheitswerte oder logische Ausdrücke zu verknüpfen. Das Berechnungsergebnis ist ebenfalls ein Wahrheitswert. In den folgenden Beispielen stehen a und b jeweils für Wahrheitswerte oder logische Ausdrücke.
| Operator | Beschreibung | in Scratch |
|---|---|---|
not a |
Logisches NICHT (“Negation”): not a ist genau dann True, wenn a zu False ausgewertet wird. |
 |
a and b |
Logisches UND: a and b ist genau dann True, wenn sowohl a als auch b zu True ausgewertet werden. |
 |
a or b |
Logisches ODER: a and b ist genau dann True, wenn a, b oder beide zu True ausgewertet werden. |
 |
Operatoren für Zeichenketten
Die folgenden Operatoren sind zum Arbeiten mit Zeichenketten (Datentyp str) hilfreich.
In der Regel ist der Ergebniswert ebenfalls eine Zeichenkette (Ausnahme: Für den Operator in ist das Ergebnis ein Wahrheitswert).
In den folgenden Beispielen stehen s und t jeweils für Zeichenketten und n für eine ganze Zahl.
| Operation | Bedeutung | in Scratch |
|---|---|---|
s + t |
Aneinanderhängen (“Konkatenation”) Beispiel: 'Flens' + 'burg' → 'Flensburg' |
 |
n * s |
Vervielfältigung Beispiel: 3 * 'Ho' → 'HoHoHo' |
|
s in t |
Ist der Teilstring t in s enthalten? Beispiel: 'sum' in 'Husum' → True |
 |
s[n] |
Zeichen an der Position n im String s Beispiel: 'Rendsburg'[1] → 'e' Achtung: In Python wird von 0 an gezählt, in Scratch von 1 an! |
 |
len(s) |
Länge des Strings s Beispiel: len('Kiel') → 4 |
 |
-
Logische Wahrheitswerte werden nach George Boole, einem Pionier der mathematischen Logik, auch als “boolesche Werte” bezeichnet (im Englischen “boolean”). ↩︎
-
Bei der Umwandlung von Dezimalzahlen mit Nachkommastellen in Ganzzahlen mit der Funktion
intwird in Python zur Null hin gerundet (bei positiven Zahlen wird also abgerundet, bei negativen aufgerundet). ↩︎ -
Es gibt für die Potenz mit beliebiger Basis keinen Block in Scratch, aber mit Hilfe der Exponentialfunktion und des natürlichen Logarithmus lässt sich die Potenz folgendermaßen umformen: \(x^y = \mathrm{e}^{y\cdot\ln(x)}\) und in Scratch umsetzen:
 ↩︎
↩︎
5.4 Funktionen und Bibliotheken
Funktionen aufrufen
Funktionen kennen wir aus der Mathematik als (vereinfacht gesagt) Rechenvorschriften, um ein oder mehrere Objekte in andere umzurechnen. Zum Beispiel erhält die Funktion \(f(x) = x^2\) einen Wert für den Parameter \(x\) und gibt dessen Quadrat als Ergebnis zurück. Nun können wir Funktionswerte wie \(f(4) = 16\) berechnen.
Dieses Konzept existiert auch in Python. Zum Beispiel existiert die Funktion round(x), die eine als Parameter übergebene Zahl x kaufmännisch rundet.
>>> round(4.2)
4
>>> round(6.66)
7
>>> round(-5)
-5
Die Schreibweise funktionsname(parameterwert) orientiert sich an der mathematischen Notation.
Funktionen definieren
In Python lassen sich auch eigene Funktionen definieren. Dieses Konzept kennen wir bereits aus der visuellen Programmierung: In Scratch können wir “neue Blöcke” erstellen, hinter denen sich selbst definierte Unterprogramme verbergen (siehe Abschnitt Unterprogramme).
In Python lassen sich mit dem Schlüsselwort def eigene Funktionen definieren. Die einfachste Form dafür lautet def Funktionsname ():
Das folgende Beispiel definiert eine Funktion bzw. Unterprogramm mit dem Funktionsnamen “waagerechte_linie”, das beim Aufruf eine Zeile mit 40 Strichzeichen in die Konsole schreibt:
def waagerechte_linie():
print('----------------------------------------')
Die erste Zeile, die mit def eingeleitet wird, nennen wir den Funktionskopf, den Rest den Funktionsrumpf. Der Funktionsrumpf enthält das eigentliche Unterprogramm, also die Anweisungen, die beim Aufruf der Funktion ausgeführt werden sollen.
Im Funktionskopf können wir zusätzlich Parameter festlegen, über die der Funktion beim Aufruf Werte übergeben werden können, die in der Funktionsausführung eine Rolle spielen. Dazu schreiben wir in die Klammern die Namen der Parameter. Bei der Abarbeitung dieser Funktion werden die Parameter dann wie lokale Variablen verwendet, die nur innerhalb der Funktion sichtbar sind. Mehrere Parameter werden mit Komma getrennt angegeben.
def unterschiedlich_lange_linie(laenge):
print('-' * laenge)
def sehr_flexible_linie(laenge, zeichen):
print(zeichen * laenge)
Beim Funktionsaufruf muss darauf geachtet werden, dass für alle Parameter geeignete Werte angegeben werden.
Die Aufrufe der drei oben definierten Funktionen könnten dann beispielsweise folgendermaßen aussehen:
>>> waagerechte_linie()
-------------------------------------------
>>> unterschiedlich_lange_linie(10)
----------
>>> sehr_flexible_linie(15, '=')
===============
>>> sehr_flexible_linie(5, '-')
-----
Die Definition einer Funktion ist für sich genommen wertlos, solange die Funktion nirgendwo im Programm aufgerufen wird. Erst beim Aufruf einer Funktion wird der Programmteil, der durch die Funktion definiert wird, ausgeführt.
Rückgabewerte
Mit dem Schlüsselwort return kann das Ergebnis einer Funktion an die Aufrufstelle zurückgegeben werden. Die Funktionsausführung endet an dieser Stelle.
def quadrat(x):
return x * x
Funktionen mit Rückgabewert können im Programm nicht nur als Anweisungen, sondern als Ausdrücke eingesetzt werden. Das bedeutet, dass sie z. B. in mathematischen Berechnungen oder Parametern von weiteren Funktionsaufrufen eingesetzt werden können.
>>> quadrat(5)
25
>>> quersumme(1234)
10
>>> quersumme(3190701205)
28
>>> quersumme(quersumme(3190701205))
10
>>> quadrat(11) + quersumme(11)
123
Funktionen können natürlich sehr viel umfangreicher sein, als nur einfache mathematische Ausdrücke auszuwerten und als Ergebnis zurückzugeben. Prinzipiell können die Unterprogramme, die in den Funktionsrümpfen stehen, beliebig komplex sein – also Anweisungssequenzen, Kontrollstrukturen, Ein- und Ausgaben sowie weitere Funktionsaufrufe enthalten.
def quersumme(zahl):
zahl_als_string = str(zahl)
summe = 0
for ziffer in zahl_als_string:
summe = summe + int(ziffer)
return summe
Lokale und globale Variablen
Dieser Abschnitt wird noch ergänzt.
Bibliotheken
Wie viele andere Programmiersprachen verfügt Python nur über sehr wenige eingebaute Funktionen, z. B. len(), int() oder range(). Diese Funktionen stellen die wichtigsten Funktionalitäten zum Programmieren und die wichtigsten Datentypen zur Verfügung. Alles, was man darüber hinaus benötigen könnte, wird von so genannten Bibliotheken zur Verfügung gestellt, wobei jede Bibliothek eine klar definierte Funktionalität erfüllt.
In Python sind einige Bibliotheken standardmäßig vorinstalliert und können mit import genutzt werden. Dazu gehören u. a.:
| Name | Zweck |
|---|---|
math |
Mathematische Funktionen wie Wurzeln, Sinus/Kosinus, Logarithmen usw. |
os |
Zugriff auf das Betriebssystem |
sys |
Zugriff auf Attribute und Funktionen des Python-Interpreters |
random |
Generieren von Zufallszahlen |
tkinter |
Programmieren von grafischen Benutzeroberflächen |
turtle |
Zeichnen von Turtle-Grafiken |
datetime |
Operationen mit Datum und Zeit |
shutil |
Komplexere Operationen auf Dateien |
Daneben lassen sich auch weitere Bibliotheken von Drittanbietern nachinstallieren. Die offizielle Sammlung von Python-Bibliotheken ist der Python Package Index (PyPI) mit der Homepage https://pypi.org. Python-Programmierende können eigene Bibliotheken erstellen und über den PyPI veröffentlichen. Dort findet man unter anderem nützliche Bibliotheken wie:
| Name | Zweck |
|---|---|
bottle |
Ein einfacher Webserver |
cryptography |
Eine Bibliothek mit kryptografischen Funktionen |
numpy |
Verbesserte mathematische Operationen |
pandas |
Ein mächtiges Werkzeug zur Datenanalyse |
pillow |
Funktionen zur Bildverarbeitung |
urllib3 |
Ein einfacher HTTP-Client |
Im PyPI sind beliebte und vielgenutzte Pakete wie die Webserver Django, Bottle und Flask zu finden, aber auch Nonsens-Pakete wie shittypackage und teilweise sogar bösartige Pakete. Darum sollte man beim Benutzen von PyPI-Paketen eine gewisse Vorsicht walten lassen und sich vorher über diese Pakete informieren.
Bibliotheken einbinden und nutzen
Zum Einbinden einer Bibliothek in ein Python-Programm wird das Schlüsselwort import verwendet. Entweder bindet man die ganze Bibliothek mit import math ein oder pickt sich einzelne Funktionen heraus, etwa die Funktion sqrt zum Berechnen der Quadratwurzel. In diesem Fall schreibt man from math import sqrt. Mit from math import * können alle Funktionen und Konstanten aus der math-Bibliothek importiert werden.
Im ersten Fall muss man dann, um auf die Konstanten und Funktionen der Bibliothek zugreifen zu können, den Namen der Bibliothek (mit Punkt getrennt) vor die Aufrufe setzen: Für \(\sqrt{4}\) schreibt man dann math.sqrt(4). Im zweiten Fall (from math import sqrt oder from math import *) schreibt man einfach sqrt(4), um die Funktion aufzurufen.
| Ganze Bibliothek importieren | Einzelne Funktionen aus einer Bibliothek importieren | Alle Funktionen aus einer Bibliothek importieren | |
|---|---|---|---|
| Einbinden | import math |
from math import sqrt |
from math import * |
| \(\sqrt{4}\) | math.sqrt(4) → 2 |
sqrt(4) → 2 |
sqrt(4) → 2 |
| \(\pi\) | math.pi→ 3.141592653589793 |
pi → Fehler, weil nur sqrt importiert wurde! |
pi → 3.141592653589793 |
| Vorteile | Keine Namensverwirrung, weil beim Funktionsaufruf der Bibliotheksname mit angegeben werden muss | Entlastet den Arbeitsspeicher, weil nur wirklich benötigte Funktionen geladen werden | Importiert eine ganze Bibliothek, ermöglicht aber kompakte Notation. |
| Nachteile | Größerer Schreibaufwand und unintuitive Notationen wie datetime.datetime |
Verwirrende Fehlermeldungen, wenn man nicht importierte Funktionen verwenden möchte | Risiko von Namensverwirrungen, z. B. gibt es ceil-Funktionen in den Bibliotheken math, numpy und torch. |
Bibliotheken in Thonny installieren
Thonny enthält eine Paket-Verwaltung für PyPI, die sich im Menü unter Extras → Verwalte Plug-Ins… aufrufen lässt.
Dieses Fenster gestattet es, im PyPI nach Paketen zu suchen:
Details zu einzelnen Bibliotheken anzuzeigen:
und Pakete zu installieren oder deinstallieren:
5.4.1 Die datetime-Bibliothek
Um Daten und Zeitangaben in Python verarbeiten zu können, nutzen wir die Bibliothek datetime.
Diese Bibliothek stellt uns u.a. die Datentypen date, time, datetime und timedelta zur Verfügung.
Datums-Objekte erzeugen
Ein neues date-Objekt kann man beispielsweise mit dem Aufruf
>>> import datetime
>>> declaration_of_independence = datetime.date(1776,7,4)
>>> print(declaration_of_independence)
1776-07-04
erzeugen. Die drei angegebenen Parameter stehen dabei für Jahr, Monat und Tag und sind verpflichtend.
Ein time-Objekt kann mit dem Konstruktor datetime.time() erzeugt werden, der Parameter für Stunde, Minute, Sekunde und Mikrosekunde (in dieser Reihenfolge) annimmt, die aber optional sind.
>>> fuenfuhrtee = datetime.time(17)
>>> print(fuenfuhrtee)
17:00:00
>>> sehr_exakte_uhrzeit = datetime.time(16, 17, 25, 172623)
>>> print(sehr_exakte_uhrzeit)
16:17:25.172623
Die Kombination aus date und time ist datetime, das alle Angaben enthält.
>>> birth = datetime.datetime(2021, 11, 27, 8, 34)
>>> print(birth)
2021-11-27 08:34:00
Die Reihenfolge der Parameter ist hier datetime(Jahr, Monat, Tag, [Stunde], [Minute], [Sekunde], [Mikrosekunde]), wobei die letzten vier Parameter optional sind und auf 0 gesetzt werden, wenn sie nicht explizit angegeben werden.
Achten Sie auf die Syntax beim Erzeugen neuer Objekte. Wenn Sie die gesamte Bibliothek mit import datetime importieren, müssen Sie datetime.datetime(...) zum Erzeugen neuer Objekte schreiben. Wenn Sie nur die Klasse datetime aus der Bibliothek datetime importieren (from datetime import datetime) müssen Sie zum Erzeugen neuer Objekte datetime(...) schreiben.
Um ein date-Objekt zu erzeugen, das auf den heutigen Tag verweist, kann die Funktion date.today() benutzt werden. datetime.now() erzeugt ein datetime-Objekt, das auf die Mikrosekunde genau auf den jetzigen Zeitpunkt verweist.
>>> print(datetime.date.today()) -->>> print(datetime.datetime.now()) -- ::Operationen auf Datums-Objekten
Die Differenz zwischen zwei Daten kann man einfach mit dem --Operator berechnen. Dabei wird ein timedelta-Objekt erzeugt, das die Differenz zwischen den beiden Daten enthält.
>>> birth = datetime.date(1912, 6, 23)
>>> death = datetime.date(1954, 6, 7)
>>> print(death - birth)
15324 days, 0:00:00
timedelta-Objekte kann man auch mit dem Aufruf datetime.timedelta([Tage], [Sekunden], [Mikrosekunden], [Millisekunden], [Minuten], [Stunden], [Wochen]) erzeugt werden, wobei alle Parameter optional sind und standardmäßig mit 0 initialisiert werden.
Mit timedelta-Objekten sind noch viel mehr Berechnungen möglich. Ein paar Beispiele:
>>> jahr = datetime.timedelta(365)
>>> woche = datetime.timedelta(7)
>>> neujahr = datetime.date(2022, 1, 1)
>>> print(neujahr + jahr) # welcher Tag ist ein Jahr nach Neujahr?
2023-01-01
>>> print(neujahr - jahr) # welcher Tag ist ein Jahr vor Neujahr?
2021-01-01
>>> print(jahr / woche) # Wie viele Wochen sind in einem Jahr?
52.142857142857146
>>> print(jahr + woche) # Wie lange dauern ein Jahr und eine Woche?
372 days, 0:00:00
>>> print(jahr - woche) # Wie lange dauert ein Jahr minus eine Woche?
358 days, 0:00:00
>>> print(jahr // woche) # Wie viele ganze Wochen passen in ein Jahr?
52
>>> print(jahr % woche) # Und wie viele Tage bleiben dann noch übrig?
1 day, 0:00:00
Ob zwei datetime-Objekte gleichzeitig sind oder welches davon später ist, kann mit den Vergleichsoperatoren ==, < und > geprüft werden. Das spätere Datum gilt hier als das größere.
>>> print(death > birth)
True
>>> print(declaration_of_independence > birth)
False
Referenzen
Didaktisch reduzierte Version
Um Daten und Zeitangaben in Python verarbeiten zu können, nutzen wir die Bibliothek datetime.
Diese Bibliothek stellt uns u.a. die Datentypen date, time, datetime und timedelta zur Verfügung.
Datums-Objekte erzeugen
Ein neues Datum kann man beispielsweise mit dem Aufruf
>>> import datetime
>>> declaration_of_independence = datetime.date(1776,7,4)
>>> print(declaration_of_independence)
1776-07-04
erzeugen. Die drei angegebenen Parameter stehen dabei für Jahr, Monat und Tag und sind verpflichtend.
Ein time-Objekt kann mit dem Konstruktor datetime.time() erzeugt werden, der Parameter für Stunde, Minute, Sekunde und Mikrosekunde (in dieser Reihenfolge) annimmt, die aber optional sind.
>>> fuenfuhrtee = datetime.time(17)
>>> print(fuenfuhrtee)
17:00:00
>>> sehr_exakte_uhrzeit = datetime.time(16, 17, 25, 172623)
>>> print(sehr_exakte_uhrzeit)
16:17:25.172623
Die Kombination aus date und time ist datetime, das alle Angaben enthält.
>>> birth = datetime.datetime(2021, 11, 27, 8, 34)
>>> print(birth)
2021-11-27 08:34:00
Die Reihenfolge der Parameter ist hier datetime(Jahr, Monat, Tag, [Stunde], [Minute], [Sekunde], [Mikrosekunde]), wobei die letzten vier Parameter optional sind und auf 0 gesetzt werden, wenn sie nicht explizit angegeben werden.
Achten Sie auf die Syntax beim Erzeugen neuer Objekte. Wenn Sie die gesamte Bibliothek mit import datetime importieren, müssen Sie datetime.datetime(...) zum Erzeugen neuer Objekte schreiben. Wenn Sie nur die Klasse datetime aus der Bibliothek datetime importieren (from datetime import datetime) müssen Sie zum Erzeugen neuer Objekte datetime(...) schreiben.
Um ein date-Objekt zu erzeugen, das auf den heutigen Tag verweist, kann die Funktion date.today() benutzt werden. datetime.now() erzeugt ein datetime-Objekt, das auf die Mikrosekunde genau auf den jetzigen Zeitpunkt verweist.
>>> print(datetime.date.today()) -->>> print(datetime.datetime.now()) -- ::Operationen auf Datums-Objekten
Die Differenz zwischen zwei Daten kann man einfach mit dem --Operator berechnen. Dabei wird ein timedelta-Objekt erzeugt, das die Differenz zwischen den beiden Daten enthält.
>>> birth = datetime.date(1912, 6, 23)
>>> death = datetime.date(1954, 6, 7)
>>> print(death - birth)
15324 days, 0:00:00
timedelta-Objekte kann man auch mit dem Aufruf datetime.timedelta([Tage], [Sekunden], [Mikrosekunden], [Millisekunden], [Minuten], [Stunden], [Wochen]) erzeugt werden, wobei alle Parameter optional sind und standardmäßig mit 0 initialisiert werden.
Mit timedelta-Objekten sind noch viel mehr Berechnungen möglich. Ein paar Beispiele:
>>> jahr = datetime.timedelta(365)
>>> woche = datetime.timedelta(7)
>>> neujahr = datetime.date(2022, 1, 1)
>>> print(neujahr + jahr) # welcher Tag ist ein Jahr nach Neujahr?
2023-01-01
>>> print(neujahr - jahr) # welcher Tag ist ein Jahr vor Neujahr?
2021-01-01
>>> print(jahr / woche) # Wie viele Wochen sind in einem Jahr?
52.142857142857146
>>> print(jahr + woche) # Wie lange dauern ein Jahr und eine Woche?
372 days, 0:00:00
>>> print(jahr - woche) # Wie lange dauert ein Jahr minus eine Woche?
358 days, 0:00:00
>>> print(jahr // woche) # Wie viele ganze Wochen passen in ein Jahr?
52
>>> print(jahr % woche) # Und wie viele Tage bleiben dann noch übrig?
1 day, 0:00:00
Ob zwei datetime-Objekte gleichzeitig sind oder welches davon später ist, kann mit den Vergleichsoperatoren ==, < und > geprüft werden. Das spätere Datum gilt hier als das größere.
>>> print(death > birth)
True
>>> print(declaration_of_independence > birth)
False
Referenzen
- Offizielle Python-Dokumentation zu
datetime(englisch) - Tutorial von GeeksforGeeks (englisch)
5.5 Kontrollstrukturen
Bedingte Verzweigung (if, elif, else)
Zur Realisierung einer Fallunterscheidung werden in Python die Schlüsselworte if, elif und else genutzt.
Bedingte Anweisung mit if
Der einfachste Fall ist eine Sequenz von Anweisungen, die nur dann ausgeführt werden soll, wenn eine bestimmte Bedingung erfüllt ist, sonst nicht. Die Schreibweise ist if Bedingung: und dann folgen die Anweisungen, die in dem Fall ausgeführt werden sollen, dass die Bedingung wahr ist. Diese Anweisungen müssen eingerückt werden, damit der Interpreter identifizieren kann, welche Anweisungen in Abhängigkeit von der Bedingung und welche immer ausgeführt werden sollen.
Im folgenden Beispiel wird die print-Anweisung nur ausgeführt, falls der Ausdruck (notendurchschnitt > 4) zu wahr (True) ausgewertet wird:
if notendurchschnitt > 4.0:
# Teil A
print('Die Klausur muss von der Schulleitung genehmigt werden.')
Bedingungen
Als Bedingung kann jeder Ausdruck eingesetzt werden, der zu True oder False ausgewertet werden kann. Hier werden also in der Regel logische Ausdrücke verwendet, zum Beispiel Vergleiche mit den Vergleichsoperatoren < (kleiner als), > (größer als) oder == (gleich).
Mehrere Vergleiche lassen sich mit den logischen Verknüpfungsoperatoren and (logisches UND) und or (logisches ODER) zu einer Bedingung verknüpfen. Im folgenden Beispiel wird die print-Anweisung ausgeführt, falls der Wert der Variablen notendurchschnitt größer als 4 oder kleiner als 1.5 ist (d. h. wenn mindestens einer der mit or verknüpften Vergleiche wahr ist):
if notendurchschnitt > 4.0 or notendurchschnitt < 1.5:
# Teil A
print('Die Klausur muss von der Schulleitung genehmigt werden.')
Werden Vergleiche dagegen mit and verknüpft, müssen alle einzelnen Vergleiche zu wahr ausgewertet werden, damit die Gesamtbedingung wahr ist:
if notendurchschnitt > 4.0 and anzahl_klausuren >= 2:
# Teil A
print('Die Klausur muss von der Schulleitung genehmigt werden.')
Alternative mit else
Um alternative Anweisungen auszuführen, wenn die Bedingung nicht erfüllt ist, wird das Schlüsselwort else: (engl. sonst) verwendet. Das else wird im Gegensatz zu den Anweisungen für den Dann- und den Sonst-Fall nicht eingerückt, steht also auf derselben Einrückungstiefe wie das if.
if notendurchschnitt > 4.0:
# Teil A
print('Die Klausur muss von der Schulleitung genehmigt werden.')
else:
# Teil B
print('Alles okay, die Klausur kannst du problemlos zurückgeben.')
Mehrfache bedingte Verzweigung mit elif
Mit elif (kurz für else if) können mehrere Bedingungen nacheinander abgeprüft werden. In diesem Fall werden die Bedingungen solange abgeprüft, bis eine davon wahr ist. Nur die Anweisungen, die zu dieser Bedingung gehören werden dann ausgeführt.
Nach einem if können beliebig viele elifs folgen. Für den Fall, dass gar keine der abgeprüften Bedingungen wahr ist, kann nach den elifs ein else folgen.
if notendurchschnitt > 4.0:
# Teil A
print('Die Klausur muss von der Schulleitung genehmigt werden.')
elif notendurchschnitt > 2.0:
print('Na, das ist doch ganz okay gelaufen.')
else:
# Teil C
print('Wow, das ist ja ein Hammer-Durchschnitt!')
Im obigen Beispiel würde ein Notendurchschnitt von 4.2 beide Bedingungen erfüllen, aber es würde nur der Text “Die Klausur muss von der Schulleitung genehmigt werden.” ausgegeben werden, da die Auswertung nach dem ersten Auffinden einer erfüllten Bedingung endet.
Bedingte Wiederholung (while)
Um eine Anweisung oder eine Sequenz von Anweisungen in Abhängigkeit von einer Bedingung zu wiederholen, nutzen wir das Schlüsselwort while, welches genau so genutzt wird wie if: nach dem while folgt eine Bedingung, die
Im folgenden Beispiel soll der Nutzer seine Postleitzahl eingeben. Die Eingabe wird geprüft und die Eingabeaufforderung wiederholt, solange wie keine Zahl eingegeben wurde:
plz = input('Bitte geben Sie Ihre Postleitzahl ein: ')
while not input.isnumeric():
# Teil C
plz = input('Das ist keine Zahl. Bitte versuchen Sie es erneut: ')
Anders als in Scratch werden hier die Anweisungen nicht wiederholt, bis die Bedingung wahr ist, sondern solange sie wahr ist. Die folgenden Code-Schnipsel sind äquivalent:
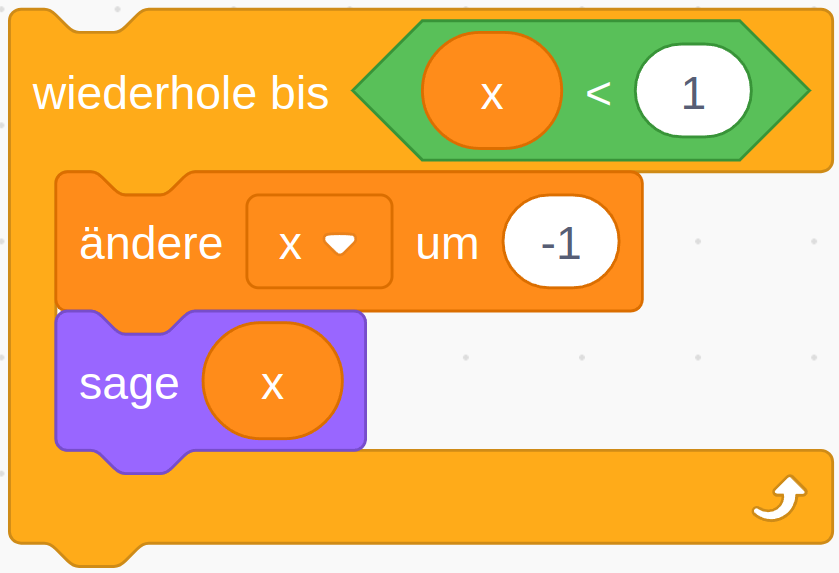
while x >= 1:
x = x - 1
print(x)
Eine endlos laufende Wiederholung lässt sich realisieren, indem nach dem while eine immer wahre Bedingung gestellt wird:
while True:
# Teil C
print('Diese Wiederholung läuft ewig.')
while 1 == 1:
# Teil C
print('Diese theoretisch auch - praktisch wird sie nie gestartet, weil die Wiederholung davor endlos läuft.')
Auch eine endlos laufende Wiederholung kann aber mit dem Schlüsselwort break unterbrochen werden. Wenn mehrere Wiederholungen ineinander geschachtelt werden, wird dabei nur die innerste unterbrochen, in der sich die break-Anweisung befindet.
Dies kann vor allem nützlich sein, wenn die Abbruchbedingung der Wiederholung sehr komplex oder mehrstufig ist. In folgendem Beispiel soll der Nutzer seine Postleitzahl eingeben. Die Eingabe wird in zwei Schritten auf Korrektheit überprüft: zuerst wird mit isnumeric() geprüft, ob der eingegebene String plz nur aus Ziffern besteht; falls dies der Fall ist, wird überprüft, ob die eingegebene Zahl zwischen 01001 und 99998 liegt und damit eine gültige deutsche Postleitzahl sein könnte. Hierbei wird die Eingabe in ein int konvertiert, was bei einer nicht-numerischen Eingabe zu einer Fehlermeldung und dem Abbruch des Programms führen würde.
while True:
plz = input('Bitte geben Sie Ihre Postleitzahl ein: ')
if not plz.isnumeric():
print('Sie haben keine Zahl eingegeben.')
elif int(plz) < 1001 or int(plz) > 99998:
print('Das ist keine gültige Postleitzahl.')
else:
break
Wiederholungen über eine Datenstruktur (for)
Das Schlüsselwort for kann man benutzen, um für alle Elemente in einer Datenstruktur dieselben Anweisungen auszuführen. Das kann eine Liste sein, ein String oder ähnliches. Die Syntax der Wiederholung ist for Element in Liste1: und danach folgen die Anweisungen, wieder eingerückt.
klassenliste = ['Felix', 'Noah', 'Leonie', 'Hanna', 'Emma', 'Nele', 'Enna', 'Hannah', 'Mohammed', 'David', 'Neven', 'Paula', 'Moritz', 'Maximilian']
print('Moin. Wer fehlt heute?')
for kind in klassenliste:
print(kind + ', bist du da?')
Wiederholungen mit fester Anzahl (range)
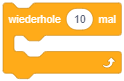
Für eine Wiederholung mit fester Anzahl, wie sie aus Scratch bekannt ist, kann die Datenstruktur range benutzt werden. Eine range zählt dabei von einem ggf. vorgegebenen Startwert zu einem vorgegebenen Endwert mit einer ggf. ebenfalls vorgegebenen Schrittweite hoch. Dies kann für eine for-Wiederholung genutzt werden. Der range können dabei bis zu drei Parameter übergeben werden:
- ein Startwert, von wo die
rangezu zählen beginnen soll, dieser ist optional und wird standardmäßig auf 0 gesetzt - ein Endwert, bei dem die
rangeaufgehört haben soll, zu zählen, dieser muss auf jeden Fall angegeben werden. - eine Schrittweite, die beim Zählen eingesetzt werden soll, diese ist optional und wird standardmäßig auf 1 gesetzt. Wenn die
rangerückwärts zählen soll, muss eine negative Schrittweite eingesetzt werden. Die Schrittweite darf nicht auf 0 gesetzt werden.
Wird nur ein Parameter übergeben, wird dieser als Endwert interpretiert, zwei Parameter werden als Start- und Endwert interpretiert.
Der übergebene Endwert wird nicht mitgezählt! Eine range(0,5) zählt also nur bis 4!
Betrachten wir das Verhalten einiger ranges:
>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(3,7))
[3, 4, 5, 6]
>>> list(range(2,18,3))
[2, 5, 8, 11, 14, 17]
>>> list(range(3,-4,-1))
[3, 2, 1, 0, -1, -2, -3]
Eine for-Wiederholung in Verbindung mit einer range lässt sich wie folgt als while-Wiederholung darstellen:
for x in range(start,finish,step):
do_some_stuff_with(x)
entspricht:2
x = start
while x < finish:
do_some_stuff_with(x)
x = x + step
Dass der Endwert, der einer range übergeben wird, nicht mitgezählt wird, hat durchaus Vorteile. Zum Beispiel kann man so die Länge einer Liste an eine range übergeben, die dann durch alle Indizes der Liste von 0 bis Länge-1 hochzählt.
-
Statt einer Liste kann jede beliebige Datenstruktur verwendet werden, die iterierbar (engl. iterable) ist, d. h. es zulässt, eine Menge an Elementen in einer gewissen Reihenfolge durchzugehen. ↩︎
-
Der Einfachheit und Lesbarkeit halber ist die
while-Wiederholung hier nur für positive Schrittweiten dargestellt. Überlegen Sie: wie müsste man die Bedingung derwhile-Wiederholung anpassen, damit sie auch für negative Schrittweiten funktionieren würde? ↩︎
5.6 Debugging
Die Abbildung rechts zeigt einen Bug, zu deutsch ein Krabbeltier, sowohl im wörtlichen als auch im übertragenen Sinne. Die abgebildete Motte hatte 1947 einen Kurzschluss in einem Computer verursacht und noch heute werden alle metaphorischen kleinen Krabbeltiere, die den Ablauf eines Computerprogramms stören, als Bugs bezeichnet1. Analog bezeichnet man das Entfernen dieser Bugs als Debugging und die dazu verwendeten Werkzeuge als Debugger. Eine analoge Form des Debuggings haben wir bereits bei der visuellen Programmierung verwendet: Trace-Tabellen.
Mithilfe eines Debuggers kann man ein Programm schrittweise durchlaufen und dabei z.B. die verwendeten Variablen oder den belegten Speicher im Auge behalten.
Thonny verfügt über einen eingebauten Debugger mit recht simpler Funktionalität, der aber für die meisten schulischen Zwecke genügt.
Die Tastenkombination [Shift]+[F5] oder das Icon mit dem Käfer ![]() starten den Debugger. Im Debug-Modus stehen dann diverse Werkzeuge zur Verfügung, um das Programm kontrolliert und schrittweise ablaufen zu lassen.
starten den Debugger. Im Debug-Modus stehen dann diverse Werkzeuge zur Verfügung, um das Programm kontrolliert und schrittweise ablaufen zu lassen.
Eins der wichtigsten Werkzeuge sind Breakpoints. Breakpoints können gezielt platziert werden, um den Programmfluss an einer bestimmten Stelle zu unterbrechen und die weitere Ausführung der Kontrolle des Entwicklers*der Entwicklerin zu überlassen.
Einen Breakpoint kann man mit einem Klick auf die Zeilennummer derjenigen Anweisung setzen, an der der Programmablauf unterbrochen werden soll. Neben dieser Zeilennummer erscheint dann ein roter Punkt ![]() .
.
Sobald der Programmablauf beim Debuggen einen Breakpoint erreicht, wird er gestoppt, die aktuell betrachtete Programmzeile farblich hervorgehoben und das weitere Vorgehen dem*der Debuggenden überlassen. Falls keine Breakpoints gesetzt sind, wird von Anfang an so verfahren.
Für das weitere Vorgehen stehen folgende Werkzeuge zur Verfügung, die entweder über die Icon-Symbolleiste oder das “Ausführen”-Menü zu erreichen sind:
| Werkzeug | Erläuterung |
|---|---|
| Die hervorgehobene Zeile wird vollständig ausgeführt und zur nächsten auszuführenden Zeile gesprungen. | |
| Komplexere Anweisungen werden so kleinschrittig wie möglich abgearbeitet. | |
| Es wird ans Ende der schrittweisen Ausführung einer komplexen Anweisung gesprungen. | |
| Der Programmablauf wird normal bis zum nächsten Breakpoint bzw. falls es keinen gibt, zum Programmende fortgeführt. | |
| Der Programmablauf wird bis zur Position des Textcursors im Programmcode fortgeführt. | |
| Zurück schreiten | Es wird einen Schritt im Programmablauf zurückgesprungen. |
Beim Eintreten geht der Debugger so kleinschrittig wie möglich vor. Die folgenden elf Screenshots illustrieren, wie eine Benutzereingabe Schritt für Schritt vom Debugger verarbeitet wird, bis am Ende die Eingabe in der Variablen startwert gespeichert worden ist:
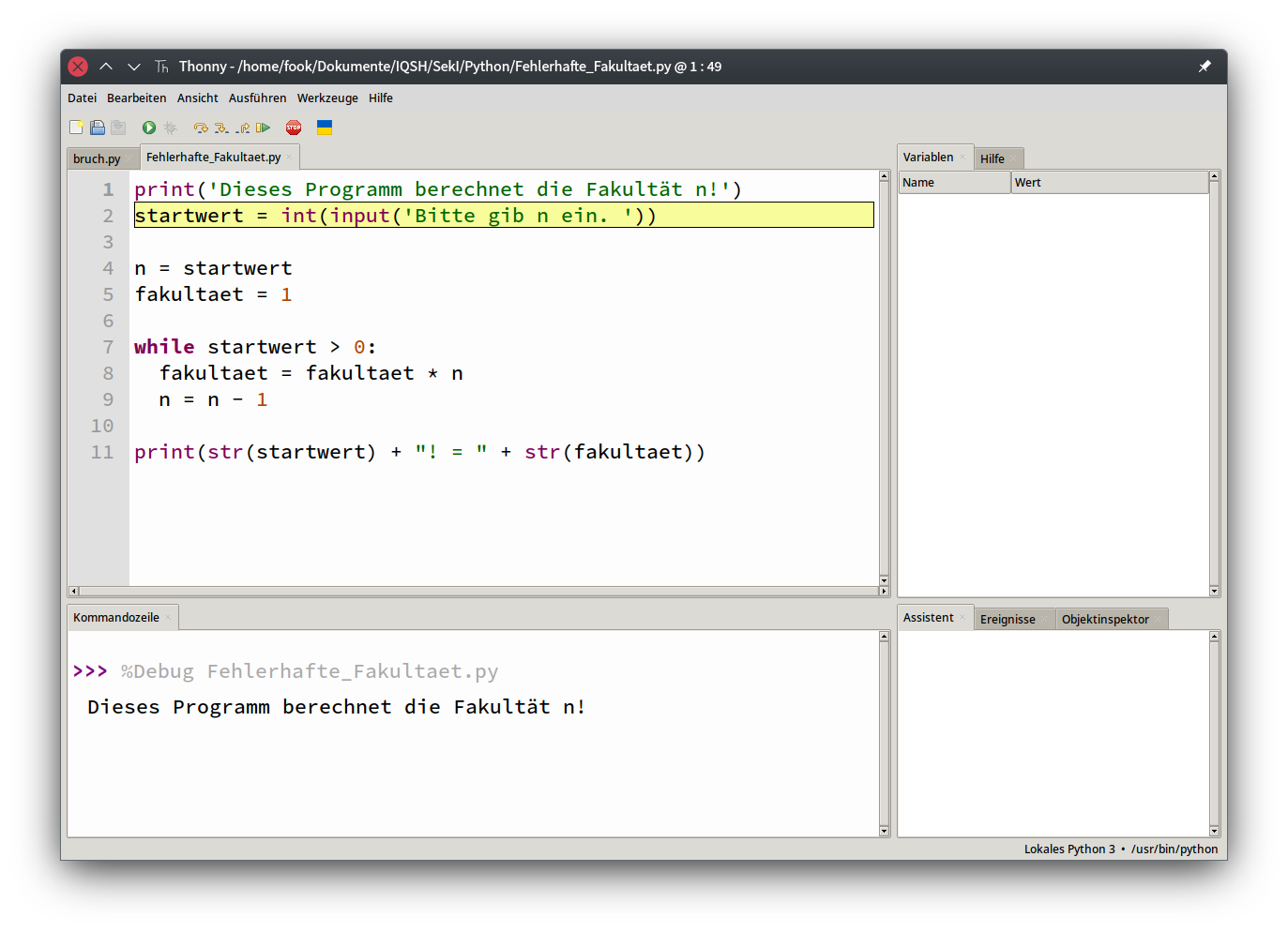 |
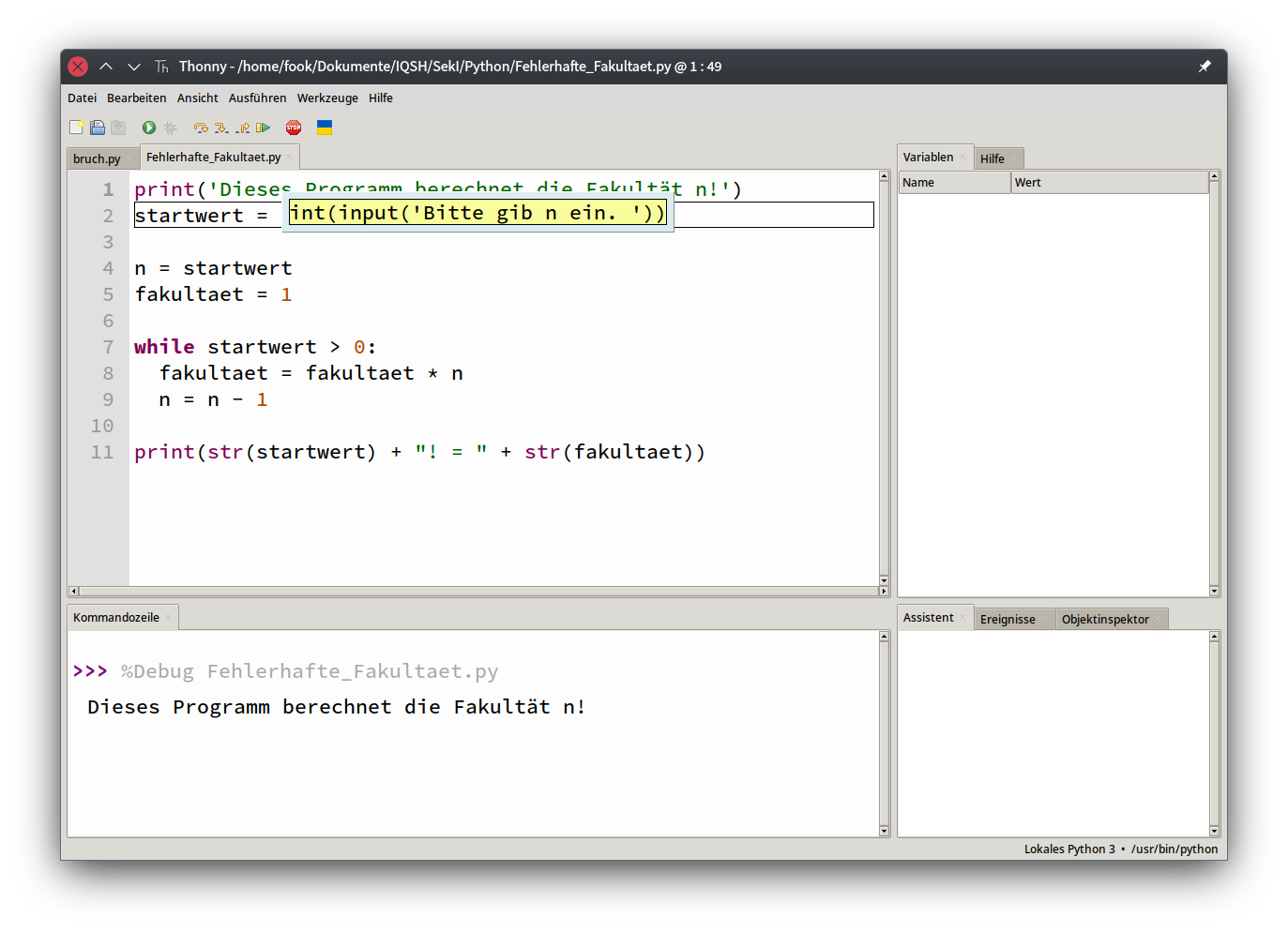 |
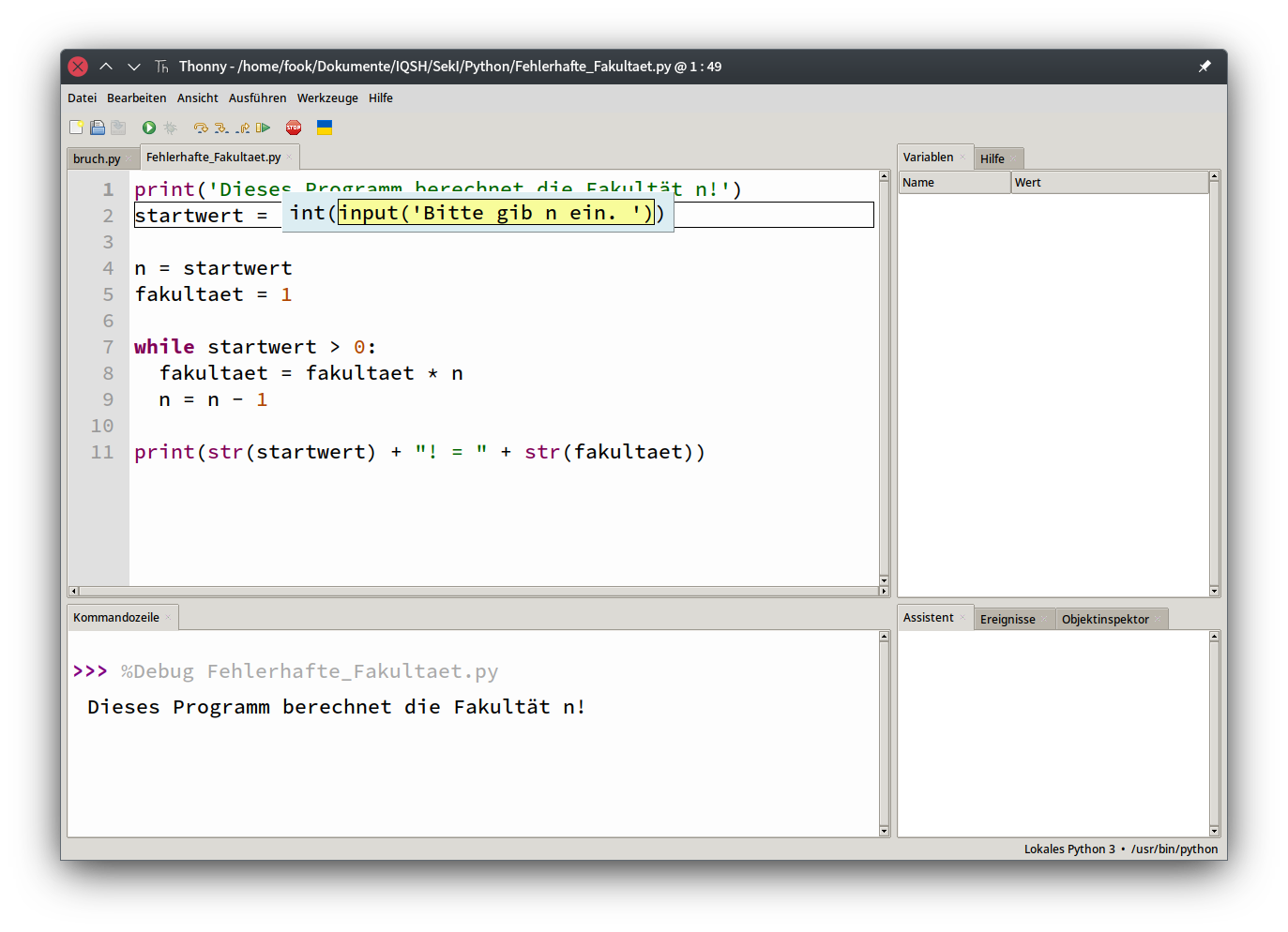 |
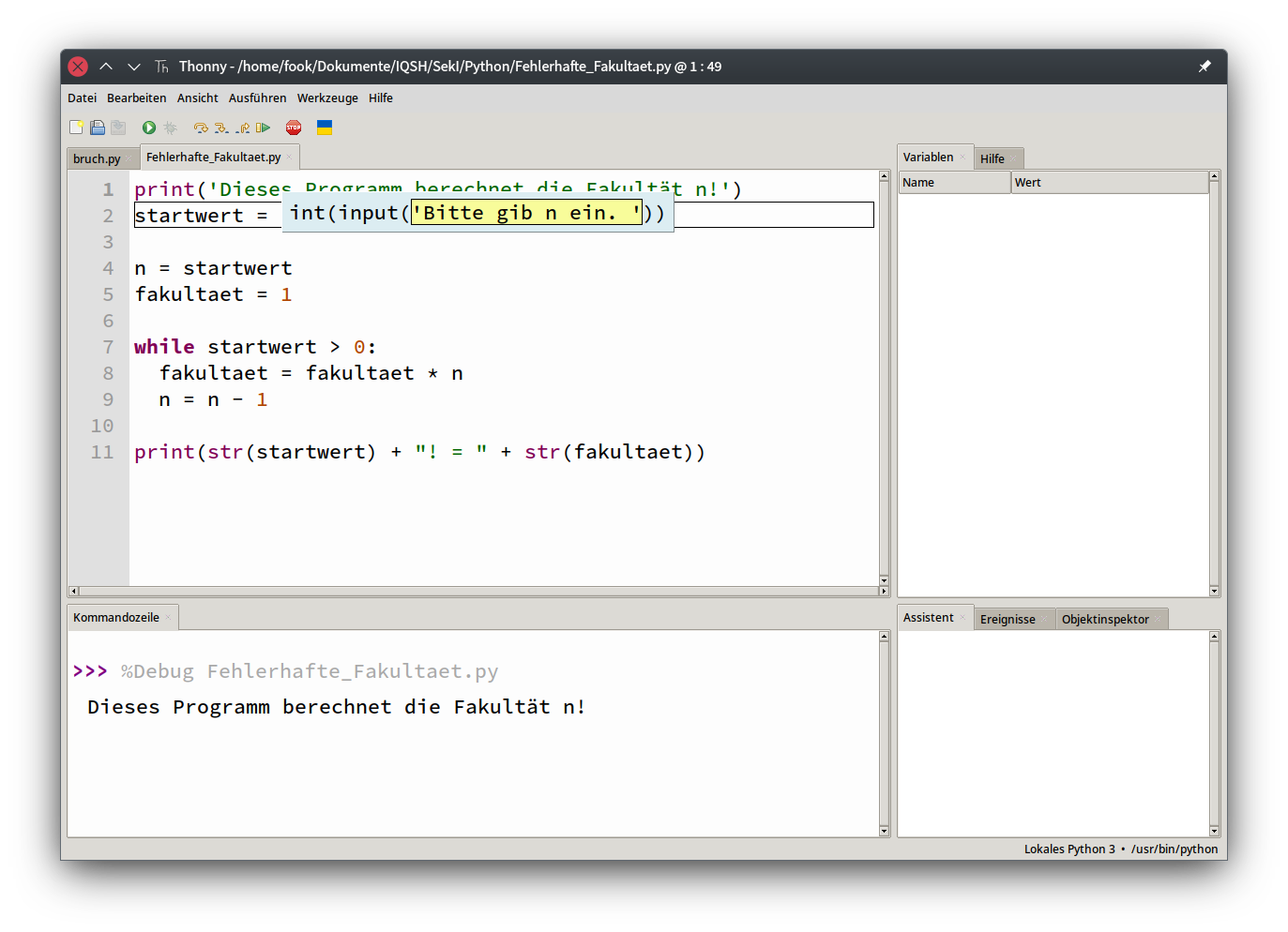 |
| Schritt 1 | Schritt 2 | Schritt 3 | Schritt 4 |
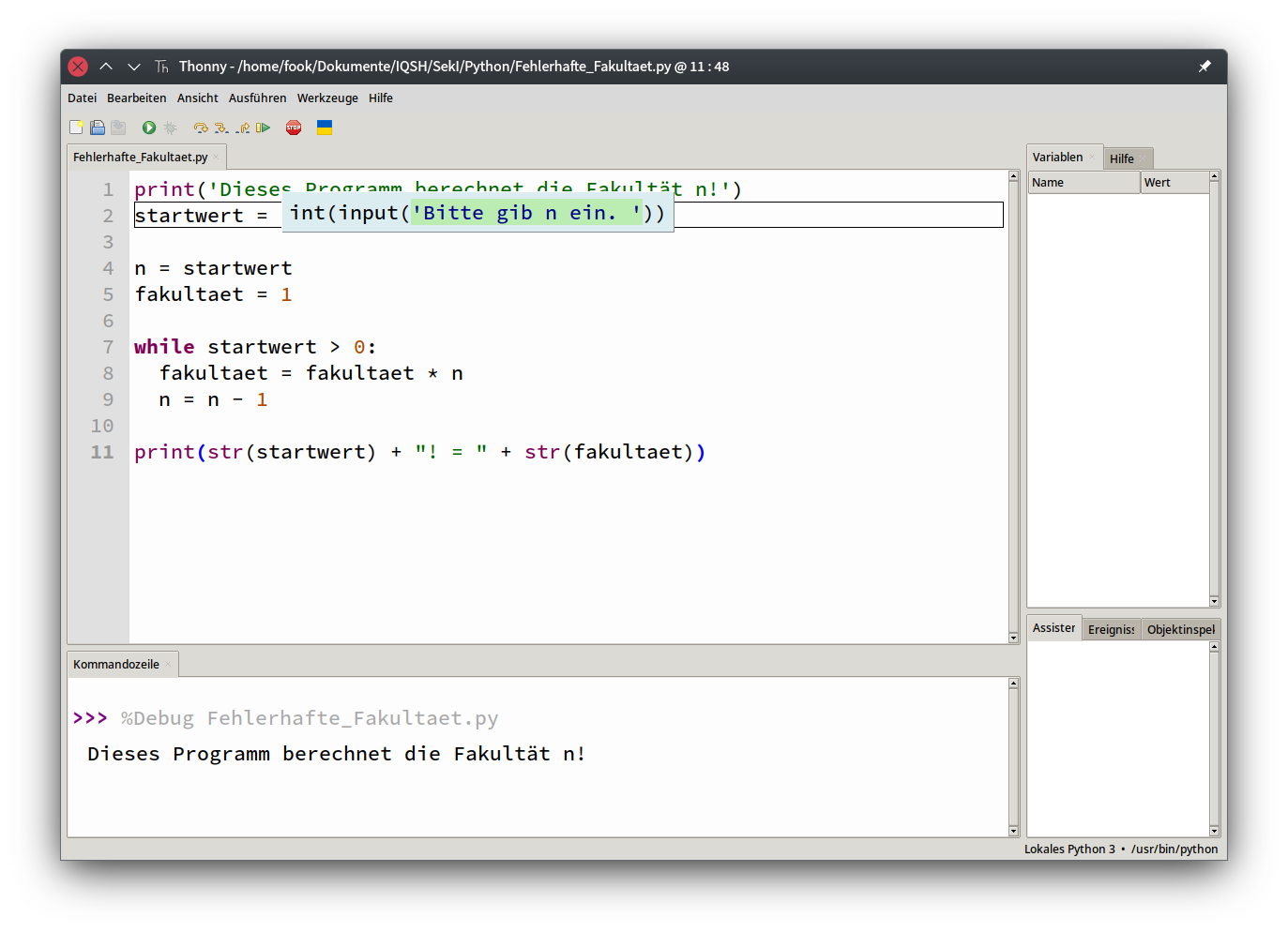 |
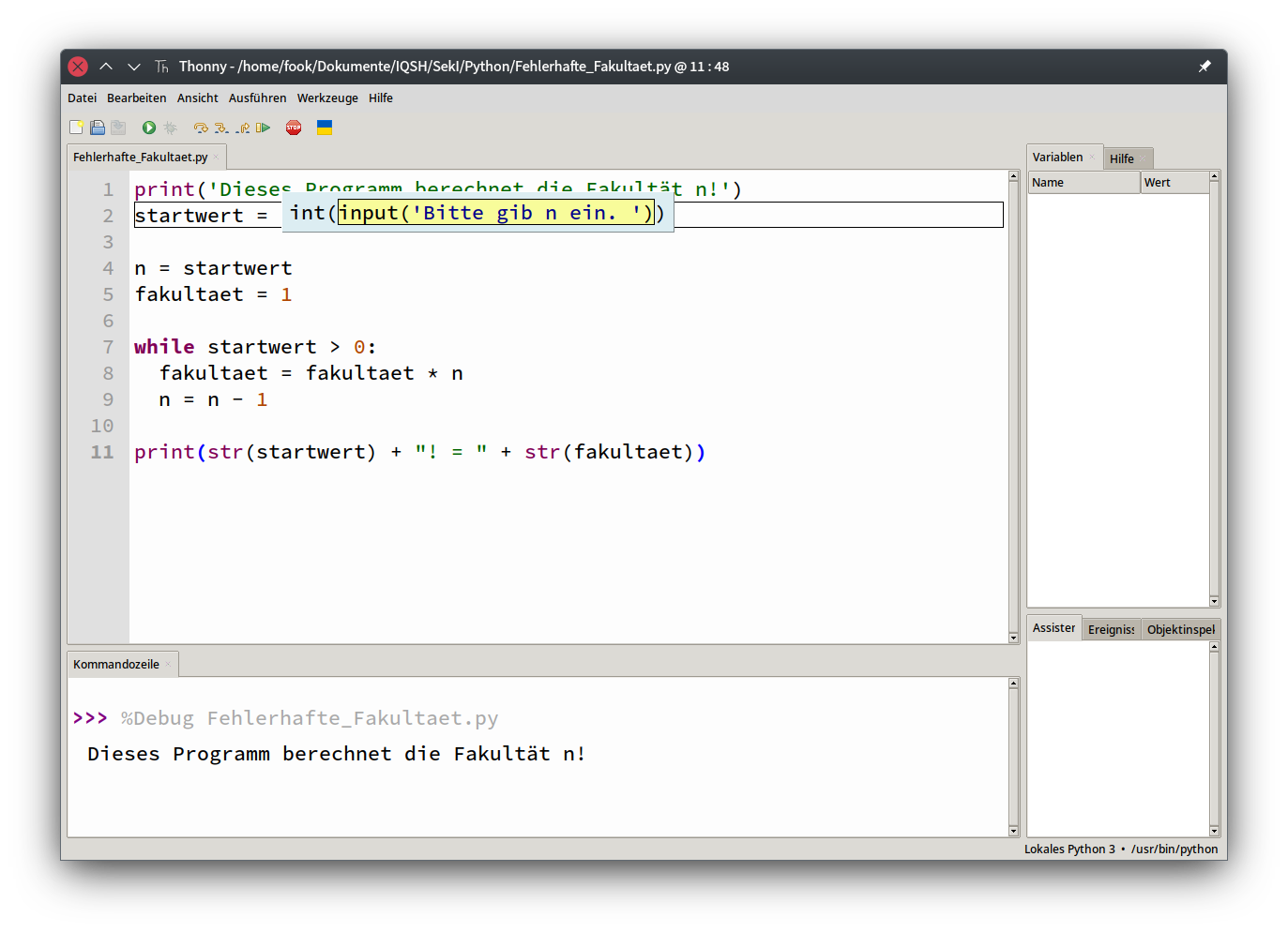 |
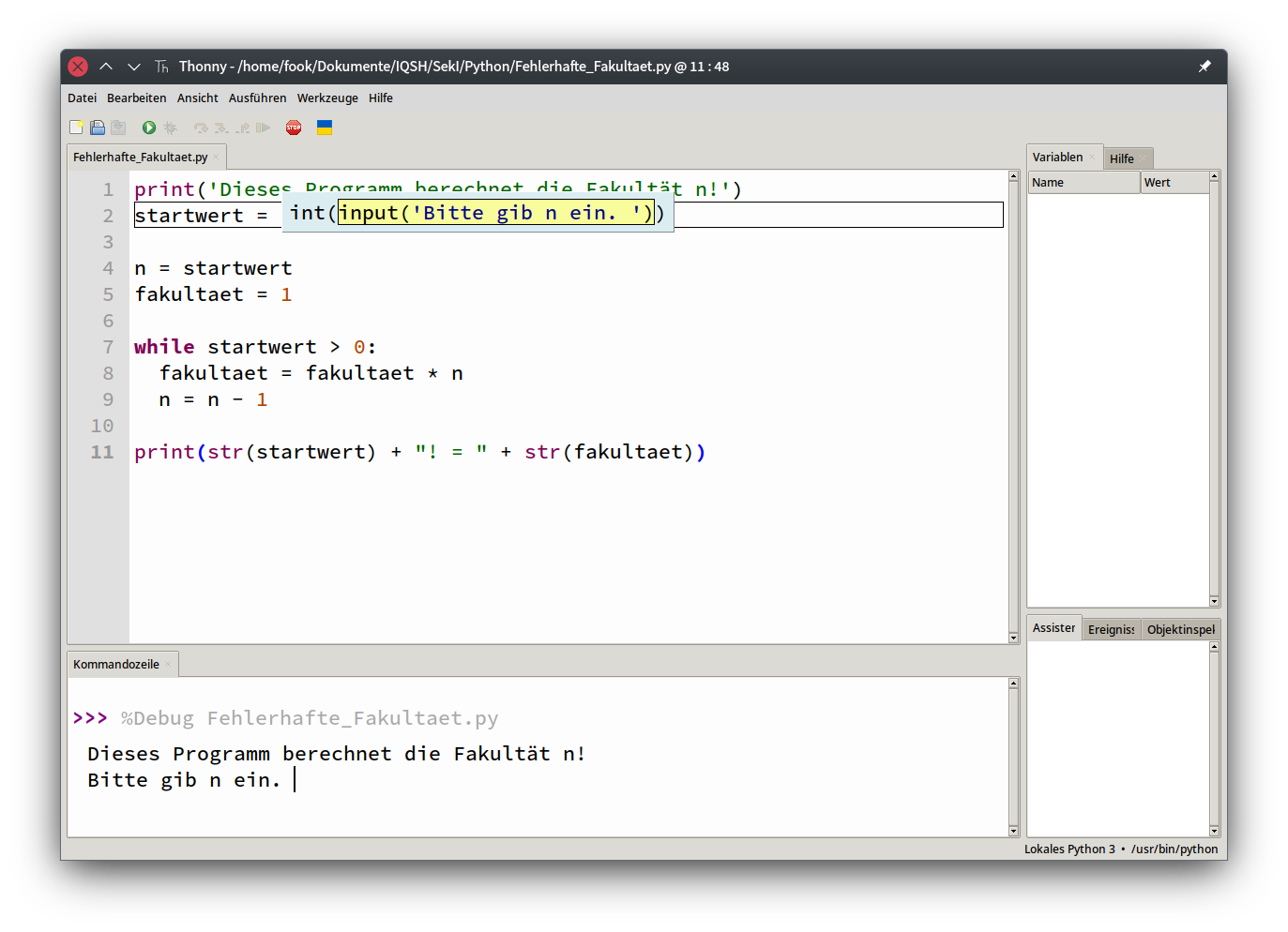 |
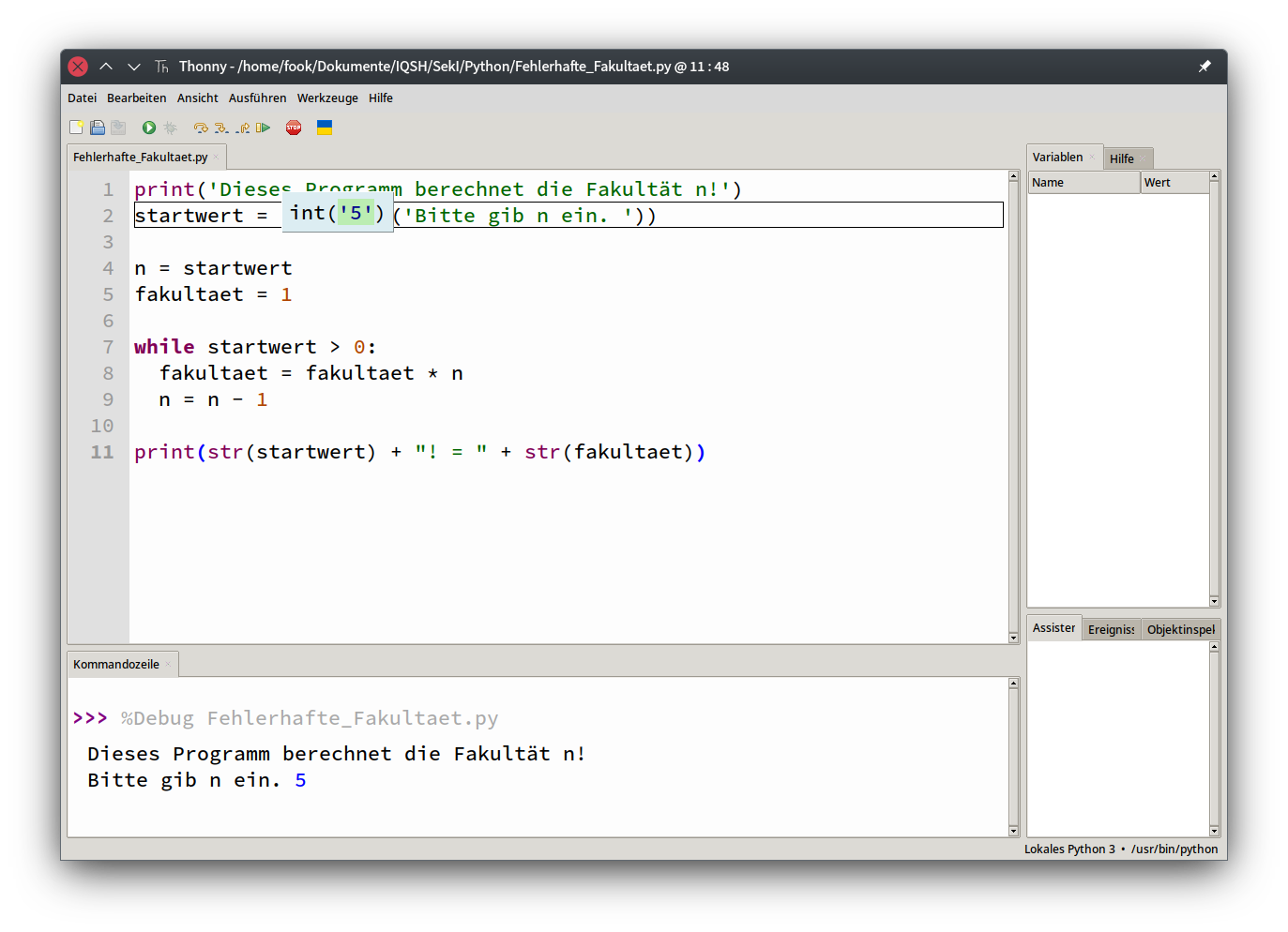 |
| Schritt 5 | Schritt 6 | Schritt 7 | Schritt 8 |
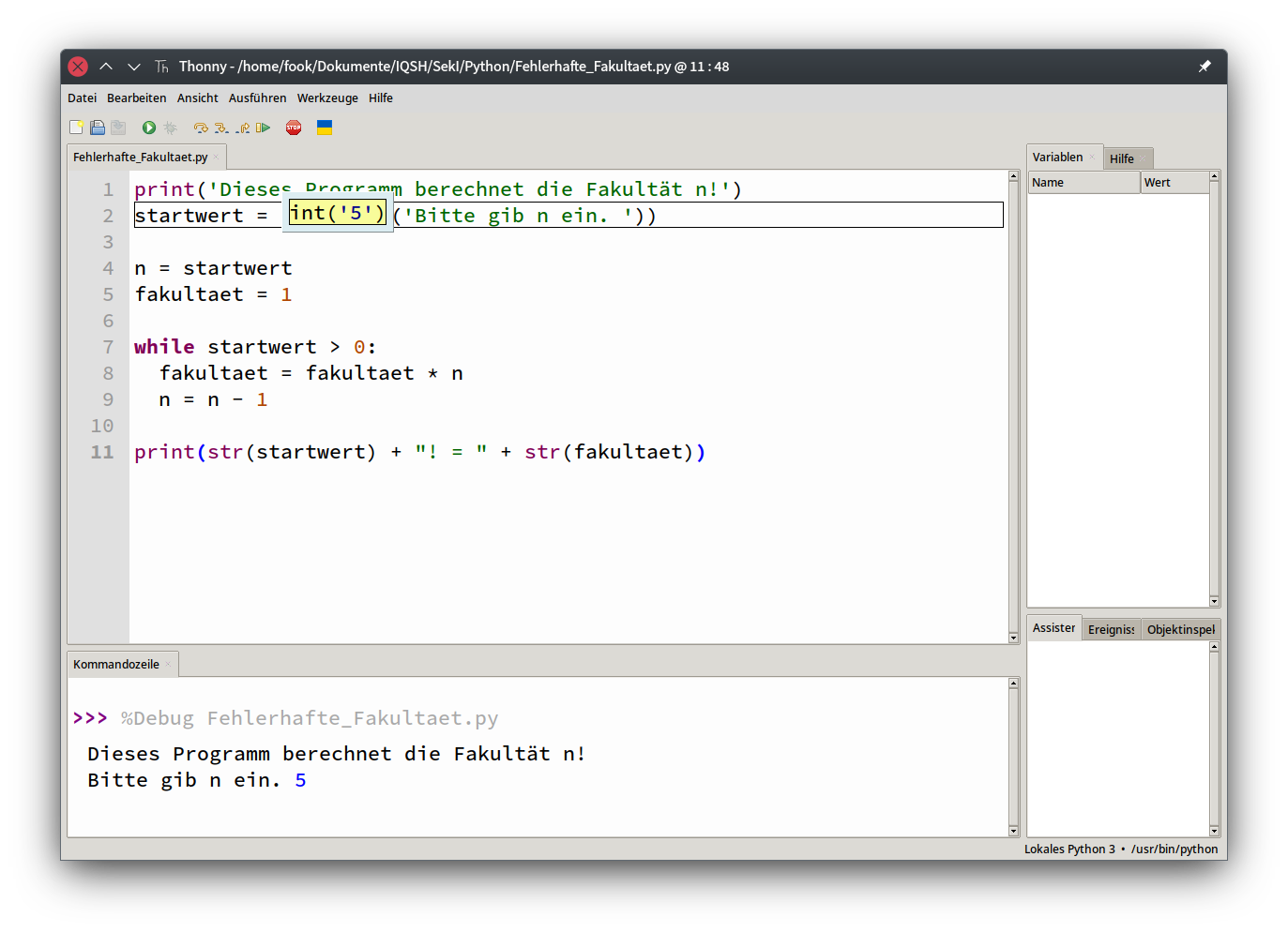 |
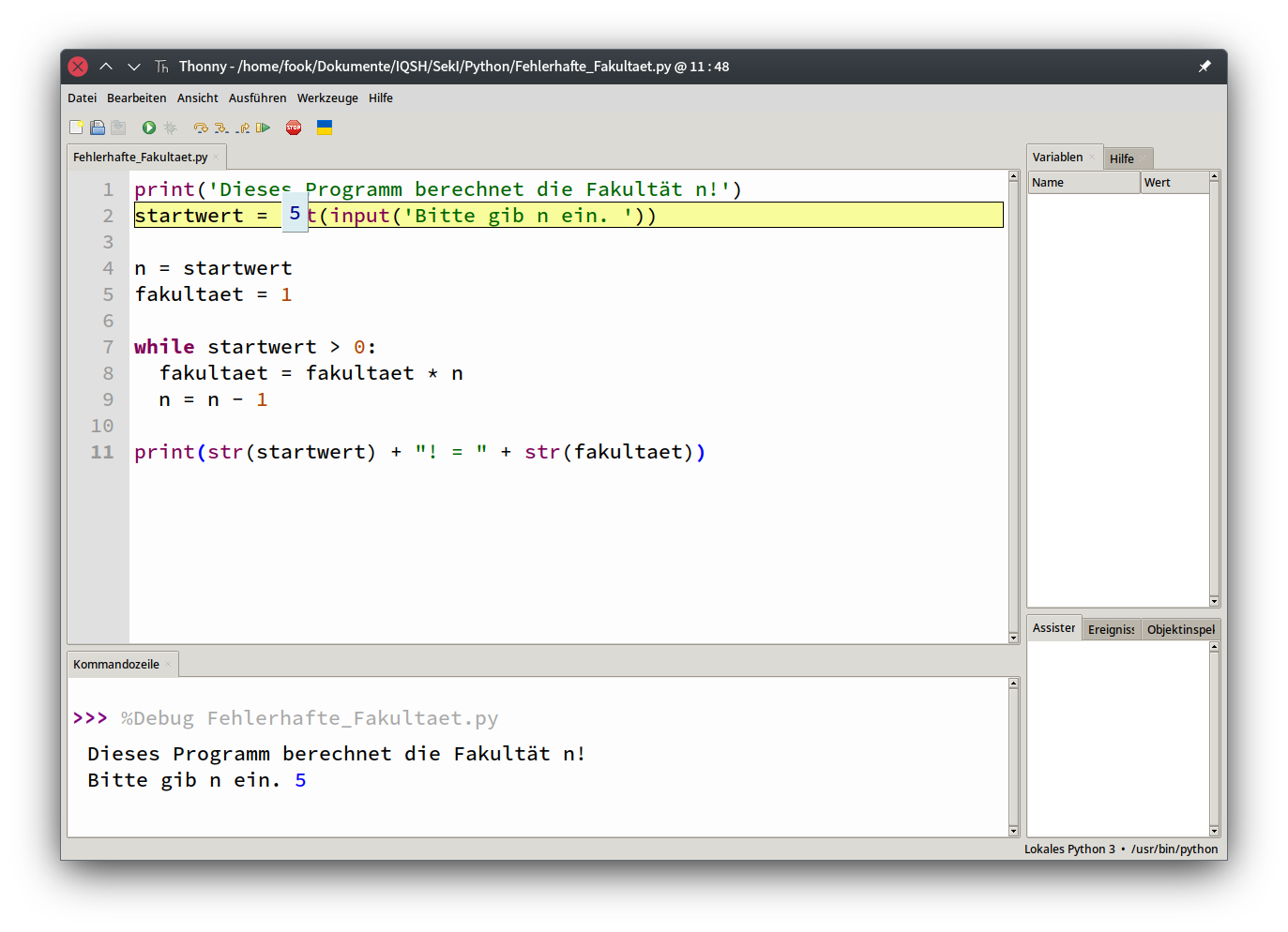 |
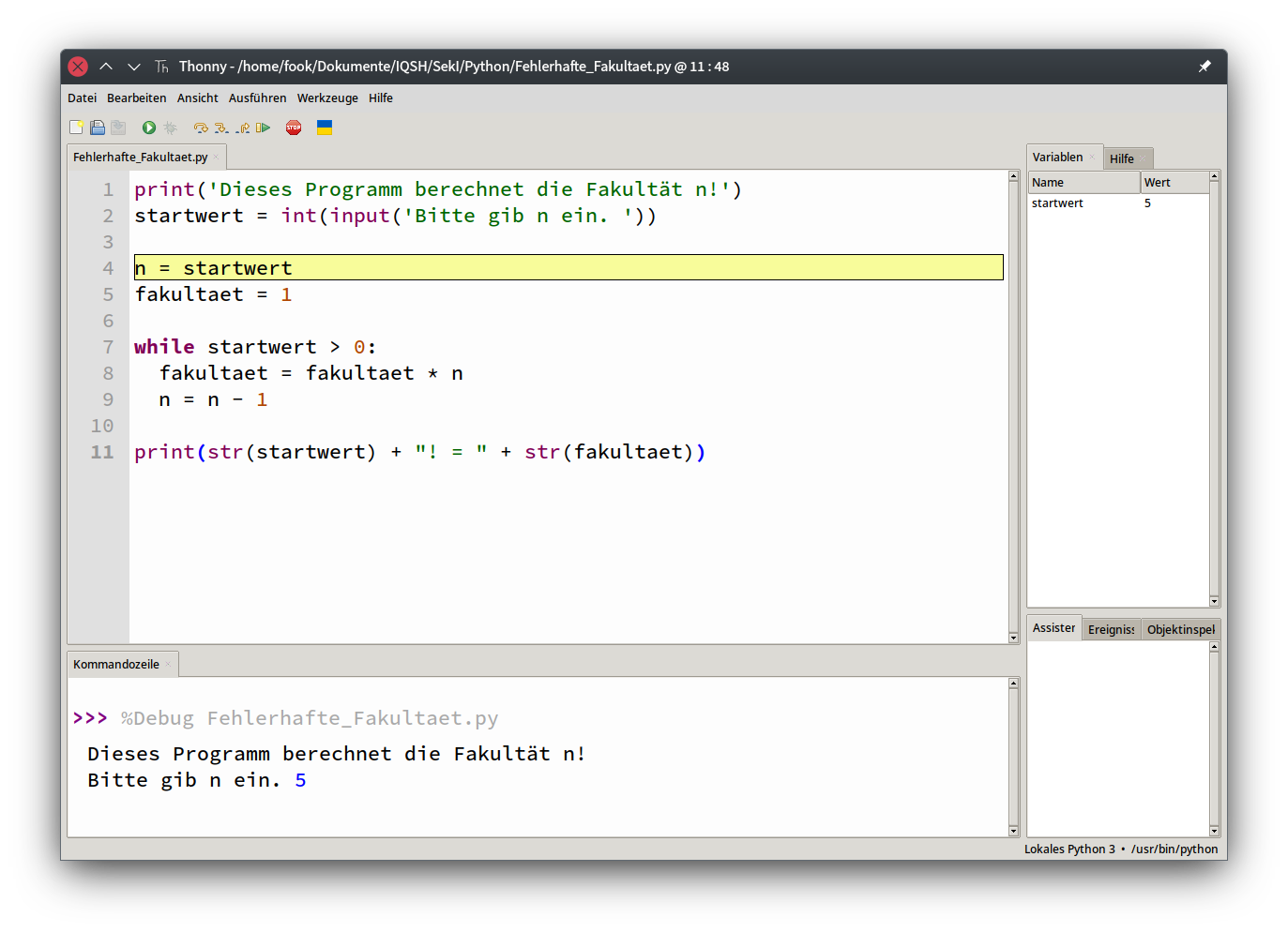 |
|
| Schritt 9 | Schritt 10 | Schritt 11 |
Insbesondere bei der Auswertung von komplexeren Ausdrücken, die nur in einigen Fällen Fehler produzieren, kann es hilfreich sein, sich nach jedem kleinsten Schritt des gegenwärtigen Zwischenstandes der Ausführung bewusst zu sein.
Besonders hilfreich ist hierbei das andockbare Variablen-Fenster. In diesem Fenster kann der Inhalt aller verwendeten Variablen eines Programms eingesehen werden. Dies funktioniert jedoch nur, wenn der Programmablauf angehalten ist; während z.B. eine besonders lange Wiederholung läuft, zeigt das Variablenfenster keine Änderungen an. In diesem Fall muss der Debugger benutzt werden, um den Ablauf der Wiederholung Schritt für Schritt nachvollziehen zu können.
-
Die Begriffe bug und debugging waren bereits lange vor dem Vorfall mit der Motte gebräuchlich, aber die Anekdote ist einfach so schön. ↩︎
5.7 Datenstrukturen
Aus der visuellen Programmierung kennen wir die Liste als Datenstruktur, um eine variable Anzahl semantisch zusammengehöriger Informationen zu speichern. Auch in Python können wir mit Listen arbeiten, darüber hinaus stehen uns aber noch weitere Datenstrukturen zur Verfügung: Tupel, Mengen und Wörterbücher.
Die grundlegenden Eigenschaften und Unterschiede zwischen den anderen drei Datenstrukturen sollen hier kurz zusammengefasst werden:
| Eigenschaft/Funktionalität | Liste | Tupel | Menge |
|---|---|---|---|
| Anzahl Elemente | variabel | fest | variabel |
| Elemente dürfen mehrmals vorkommen | ja | ja | nein |
| Elemente dürfen verändert werden | ja | nein | nein |
| Reihenfolge der Elemente | fest | fest | beliebig |
| Definition | a = [42, True, 'Hello'] |
b = (42, True, 'Hello') |
c = {42, True, 'Hello'} |
| Element an Position $x$ abrufen | a[x] |
b[x] |
nicht möglich, da Mengen keine Reihenfolge haben |
| Größe bestimmen | len(a) |
len(b) |
len(c) |
| Element hinzufügen | a.append(3.141) |
nicht möglich, da die Länge von Tupeln beschränkt ist | c.add(3.141), hat keine Auswirkung, wenn das Element schon vorher in der Menge enthalten war. |
| Prüfen, ob $x$ enthalten ist | x in a |
x in b |
x in c |
Slicing
Python gestattet nicht nur den Zugriff auf einzelne Elemente einer Liste, sondern ermöglicht auch unkompliziert das Erstellen von Teillisten, das so genannte Slicing. Dafür können bis zu drei Indizes angegeben werden:
- der Beginn der Teilliste
- das erste Element, das nicht mehr Teil der Teilliste sein soll
- der Abstand zwischen den Elementen der Teilliste
Notiert werden diese Indizes durch Doppelpunkte getrennt in eckigen Klammern hinter dem Namen der Liste, also Liste[Start:Ende:Schritt].
Alle drei Indizes können leer gelassen werden. In diesem Fall werden folgende Standardwerte eingesetzt:
0für den Beginnlen(Liste)für das Ende1für die Schrittweite
>>> a = [1,2,3,4,5,6,7,8,9,10]
>>> a[3:7]
[4, 5, 6, 7]
>>> a[3:]
[4, 5, 6, 7, 8, 9, 10]
>>> a[:5]
[1, 2, 3, 4, 5]
>>> a[1:7:2]
[2, 4, 6]
>>> a[1::2]
[2, 4, 6, 8, 10]
>>> a[:7:2]
[1, 3, 5, 7]
>>> a[::]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Für alle Indizes können auch negative Werte eingesetzt werden. Dies bedeutet, dass vom Ende der Liste an gezählt wird statt vom Anfang. Ein Start- oder End-Index von -1 bezieht sich also auf das letzte Element der Liste. Wenn der Endwert kleiner ist als der Startwert, kann eine negative Schrittweite angegeben, um die Elemente rückwärts aufzuzählen
>>> a[2:-2]
[3, 4, 5, 6, 7, 8]
>>> a[-9:7]
[2, 3, 4, 5, 6, 7]
>>> a[-5:-1]
[6, 7, 8, 9]
>>> a[-5:-1:2]
[6, 8]
>>> a[-1:-7:-2]
[10, 8, 6]
>>> a[7:3]
[]
>>> a[7:3:-1]
[8, 7, 6, 5]
>>> a[::-2]
[10, 8, 6, 4, 2]
Strings als Sonderfall von Listen
Strings werden in vieler Hinsicht wie Listen behandelt und unterstützen einige Listenoperationen, insbesondere Slicing:
>>> b = 'Panamakanal'
>>> b[5]
'a'
>>> b[1::2]
'aaaaa'
>>> b[::-1]
'lanakamanaP'
>>> 'e' in b
False
>>> 'n' in b
True
>>> len(b)
11
Anders als Listen können Strings aber nicht verändert werden:
>>> a[2] = 0
>>> a
[1, 2, 0, 4, 5, 6, 7, 8, 9, 10]
>>> a.append(11)
>>> a
[1, 2, 0, 4, 5, 6, 7, 8, 9, 10, 11]
>>> b[1] = 'e'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: 'str' object does not support item assignment
>>> b.append('?')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AttributeError: 'str' object has no attribute 'append'
Exkurs: Wörterbücher
Wörterbücher, englisch dictionaries, sind eine Schlüssel-Wert-Datenstruktur, d.h. die Daten werden in Paaren von einem Schlüssel und einem dazugehörigen Wert abgelegt. Mithilfe des Schlüssels kann der Wert dann effizient gefunden werden.
>>> englischvokabeln = {'cat': 'Katze', 'dog': 'Hund', 'mouse': 'Maus'}
>>> englischvokabeln
{'cat': 'Katze', 'dog': 'Hund', 'mouse': 'Maus'}
Es gibt zwei Möglichkeiten, einen Wert mithilfe eines Schlüssels aus einem Wörterbuch abzufragen:
-
Man setzt den Schlüssel wie einen Listen-Index in eckige Klammern; dies führt zu einer Fehlermeldung, wenn man einen nicht vorhandenen Schlüssel abfragt:
>>> englischvokabeln['cat'] 'Katze' >>> englischvokabeln['dog'] 'Hund' >>> englischvokabeln['duck'] Traceback (most recent call last): File "<stdin>", line 1, in <module> KeyError: 'duck' -
Man verwendet die
get-Methode; die Abfrage eines nicht vorhandenen Schlüssels sorgt dann dafür, dass ein Standardwert zurückgegeben wird, den man optional ebenfalls angeben kann:>>> englischvokabeln.get('dog') 'Hund' >>> englischvokabeln.get('duck') >>> englischvokabeln.get('dog', 'Das weiß ich nicht') 'Hund' >>> englischvokabeln.get('duck', 'Das weiß ich nicht') 'Das weiß ich nicht'
Mit den Methoden keys, values und items können die Schlüssel, Werte und Schlüssel-Wert-Paare des Wörterbuches in Form von Listen ausgewertet werden:
>>> englischvokabeln.keys()
dict_keys(['cat', 'dog', 'mouse'])
>>> englischvokabeln.values()
dict_values(['Katze', 'Hund', 'Maus'])
>>> englischvokabeln.items()
dict_items([('cat', 'Katze'), ('dog', 'Hund'), ('mouse', 'Maus')])
5.8 Objekte
Objekte
Den Begriff Objekt haben wir bereits im Kapitel über visuelle Programmierung kennengelernt. Genau wie Scratch ist auch Python eine objektorientierte Sprache. Das heißt, dass jeder Bestandteil der Ausführung eines Python-Programms als ein Objekt behandelt wird, das eine Identität, einen Zustand und ein definiertes Verhalten aufweist.
Objektorientierte Programmierung ermöglicht eine sehr genaue Kontrolle darüber, welche Programmteile welche Funktionen ausführen dürfen. Insbesondere behalten die Objekte selbst die Kontrolle über ihre Daten.
Beispiel: Stellen wir uns eine fiktive Software vor, die ein Bankkonto implementiert. In diesem Fall möchte man aus einer Vielzahl von Gründen Änderungen am Kontostand nicht uneingeschränkt der ganzen Software ermöglichen:
- Es gibt für die meisten Konten ein Abbuchungslimit, das überprüft werden muss.
- Ebenso muss überprüft werden, ob die Abbuchung den Disporahmen ausschöpfen würde.
- Wenn das Konto dadurch ins Minus gerät, müssen Dispozinsen erhoben und der Kunde ggf. benachrichtigt werden.
- Verdächtige Abbuchungen müssen überprüft und ggf. mit dem Kunden besprochen werden.
Durch die objektorientierte Programmierung kann man diese Zugriffsbeschränkungen den Konto-Objekten überlassen. Dadurch wird der ganze Code, der das Verhalten dieses Objekts kontrolliert, an einer Stelle konzentriert und der Zugriff darauf kann den anderen Objekten besser verwehrt werden.
Ähnliches gibt es in der visuellen Programmierung, wo man z.B. die Position eines anderen Objektes zwar abfragen, aber nicht selbsttätig verändern kann. Die einzige Möglichkeit dazu wäre, eine Nachricht an das andere Objekt zu schicken und es zu bitten, seine Position zu verändern.
Dieses Prinzip, Daten und Informationen vor dem Zugriff von außen zu verbergen und nur über definierte Schnittstellen zuzulassen, nennt man Kapselung.
Klassen
Objekte sind in Python immer Instanzen von Klassen.
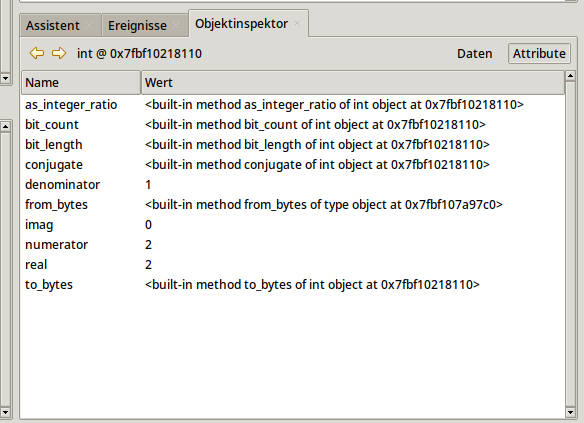
Die Identität eines Objektes wird definiert über seine(n) Namen. Namen sind in Python Referenzen, die auf Stellen im Objektspeicher verweisen, an denen die Objektdaten liegen. Mit Thonnys Objekt-Inspektor können wir uns zu jedem Objekt Details anzeigen lassen, wie die Abbildung zeigt.
Bei dem betrachteten Objekt handelt es sich um die Zahl 1, auch diese ist in Python (anders als in anderen objektorientierten Sprachen wie Java) ein Objekt mit Attributen und Methoden.
Oben im Objekt-Inspektor steht int @ 0x7fbf10218110, Typ und Speicheradresse des Objekts. Wenn man diese Informationen in einem Python-Programm benötigen sollte, kann man sie mit type(x) und id(x) abfragen.
Gleichheit und Identität
“Das gleiche” ist nicht dasselbe wie “dasselbe”. Zwei Python-Objekte sind gleich, wenn sie den gleichen Wert haben. Die Gleichheit wird mit dem Operator == abgeprüft.
>>> a = 5
>>> b = 5
>>> c = 'hello'
>>> d = 'hello'
>>> e = [1,2,3]
>>> f = [1,2,3]
>>> a == b
True
>>> c == d
True
>>> e == f
True
>>> a == c
False
>>> a == f
False
Zwei Python-Objekte sind identisch, wenn ihre Bezeichner auf dieselbe Speicheradresse verweisen. Atomare Daten wie Zahlen oder Strings, die gleich sind, sind in der Regel auch identisch. Auf zusammengesetzte Datentypen wie Listen trifft dies jedoch nicht zu. Die Identität wird mit dem Operator is abgeprüft.
>>> a = 5
>>> b = 5
>>> c = 'hello'
>>> d = 'hello'
>>> e = [1,2,3]
>>> f = [1,2,3]
>>> a is b
True
>>> c is d
True
>>> e is f
False
>>> a is c
False
>>> a is f
False
Wenn mehrere Objekte identisch sind und man eines davon verändert, verändern sich ebenso alle anderen, da sie alle auf dieselbe Speicherstelle verweisen:
>>> a = [1,2,3]
>>> b = [1,2,3]
>>> c = a
>>> a is b
False
>>> a is c
True
>>> b is c
False
>>> a.append(4)
>>> b
[1, 2, 3]
>>> c
[1, 2, 3, 4]
Mit der copy-Methode können Kopien von Objekten angelegt werden, die zwar gleich, aber nicht identisch sind.
>>> d = a.copy()
>>> a == d
True
>>> a is d
False
6. Links
6.1 Materialsammlungen
Auf dieser Seite finden Sie Links zu Materialsammlungen aus anderen Weiterbildungen zur Informatik in der Sekundarstufe I, sowie Materialien für die Unterrichtsgestaltung, die zum Teil auch in dieser Weiterbildung behandelt werden. Die Sammlung wird nach und nach erweitert und um Informationen ergänzt.
Weiterbildungen
- Weiterbildung Informatik Sek. I Baden-Württemberg: https://lehrerfortbildung-bw.de
- Weiterbildung Informatik Sek. I Niedersachsen: https://www.nibis.de
- Materialsammlung Uni Göttingen: https://www.uni-goettingen.de
- Weiterbildung Informatik Sek. I Nordrhein-Westfalen
- Materialsammlung Uni Wuppertal: https://ddi.uni-wuppertal.de
- Weiterbildung Informatik Sek. I Rheinland-Pfalz: https://informatik.bildung-rp.de
- Moodle-Kurs mit Unterrichtsmaterialien: https://lms.bildung-rp.de/austausch
- Unterstützungsystem Informatik Mecklenburg-Vorpommern: https://schule.informatik.uni-rostock.de
Unterrichtsmaterialien
- Elektronisches Schulbuch inf-schule: https://www.inf-schule.de
- Bildungsserver Berlin-Brandenburg: https://bildungsserver.berlin-brandenburg.de
- AppCamps: https://appcamps.de
- Fobizz: https://plattform.fobizz.com/unterrichtsmaterialien
- IT2School: https://www.wissensfabrik.de/mitmachprojekte/weiterfuehrende-schule/it2school
- CS Unplugged: https://csunplugged.org/de
- CS Unplugged Classics (englisch): https://classic.csunplugged.org
- Deutsche Übersetzung im Projekt ADA: https://www.ada.wien/cs-unplugged-materialiensammlung
Fachdidaktik
- Homepage von Peer Stechert: https://berufsinformatik.de
- YouTube-Kanal “Informatik-Didaktik kurzgefasst”: https://www.youtube.com/channel/UCw4vXnOoHHNSwJGfgOVf2DQ
Programmierwettbewerbe
- Bundeswettbewerb Informatik (u. a. Informatik-Biber): https://bwinf.de
- Internationale Informatik-Olympiade (IOI): https://ioinformatics.org
- Software-Challenge: https://software-challenge.de
Programmierung
Scratch
- Offizielle Scratch-Website: https://scratch.mit.edu
- Ressourcen für Lehrkräfte: https://scratch.mit.edu/educators/#resources
- Projektideen und Tutorials zu Scratch: https://scratch.mit.edu/ideas
- Veröffentlichte Projekte der Community: https://scratch.mit.edu/explore/projects/all
- Offizielles Scratch-Wiki: https://de.scratch-wiki.info/ (deutsch), https://en.scratch-wiki.info (englisch)
- Scratch-Ed Online-Community (englisch): https://scratched.gse.harvard.edu
- Scratch Encore – Unterrichtsmaterialien nach dem Use-Modify-Create-Modell (englisch): https://www.canonlab.org/scratch-encore
- Deutsche Übersetzung auf der Homepage von Peer Stechert: https://berufsinformatik.de/scratch
- Unterrichtsmaterialien der Pädagogischen Hochschule Zürich (PHZH): https://tiny.phzh.ch/scratch
- Unterrichtsmaterialien auf dem Bildungsserver Berlin-Brandenburg: https://bildungsserver.berlin-brandenburg.de/scratch
- Unterrichtsmaterialien bei AppCamps: https://appcamps.de/unterrichtsmaterial/scratch
- Unterrichtsmaterialien bei Fobizz: https://fobizz.com/unterrichtsmaterialien-zum-thema-scratch
Python
- Online-Lehrbuch zur Python-Programmierung in der Lernumgebung TigerJython: http://www.programmierkonzepte.ch
HTML & CSS
- W3Schools (englisch): https://www.w3schools.com
- Umfangreiche Tutorials, Referenzen und Übungsaufgaben zur Webentwicklung, unter anderem zu HTML und CSS
- SELFHTML: https://selfhtml.org
- Deutschsprachige Dokumentation zu HTML/CSS mit Tutorials und Referenzen im Wiki, sowie Forum zum Austausch
6.2 Software-Werkzeuge
Auf dieser Seite finden Sie einen Überblick über die Software, die im Rahmen der Weiterbildung verwendet wird, sowie über weitere Werkzeuge zur Unterstützung Ihres Unterrichts. Die Sammlung wird nach und nach erweitert und um Informationen ergänzt.
Programmierwerkzeuge
Visuelle Programmierung
- Scratch: Visuelle Programmiersprache und Entwicklungsumgebung, als Online- und Offline-Anwendung vorhanden
- Entwickler: MIT Media Lab
- Lizenz: 3-Klausel-BSD
- Offizielle Website: https://scratch.mit.edu
- Link zur Online-Entwicklungsumgebung: https://scratch.mit.edu/projects/editor
- Wikipedia-Eintrag: https://de.wikipedia.org/wiki/Scratch_(Programmiersprache)
- Wikis: https://en.scratch-wiki.info (englisch), https://de.scratch-wiki.info (deutsch)
- ScratchEd Online Community (didaktische Hinweise): https://scratched.gse.harvard.edu
Textuelle Programmierung
- Thonny: Didaktisch orientierte Entwicklungsumgebung für Python
- Entwickler: Aivar Annamaa (Universität Tartu) u. a.
- Lizenz: MIT-Lizenz (Open Source)
- Offizielle Website: https://thonny.org
- TigerJython: Didaktisch orientierte Entwicklungsumgebung für Python
- Entwickler: TigerJython Group, u. a. Tobias Kohn (ETH Zürich), Aegidius Plüss (Uni Bern)
- Lizenz: frei
- Offizielle Website: http://www.jython.ch
- Link zur Online-Entwicklungsumgebung: https://webtigerjython.ethz.ch
- Online-Lehrbuch zu TigerJython: http://www.programmierkonzepte.ch
Webentwicklung
- W3Schools Online Code Editor: Online-Editor zum Bearbeiten und Anzeigen von HTML-Dokumenten im Browser (im Rahmen der W3Schools-Tutorials zu HTML und CSS)
- Link zum Online-Editor: https://www.w3schools.com/tryit
- Glitch: Online-Entwicklungsumgebung zum Bearbeiten und Anzeigen von HTML/CSS im Browser (auch umfangreichere Projekte aus mehreren Dateien), die sich online bereitstellen und remixen lassen
- Kosten: “Starter”-Version kostenlos nutzbar, hier sind alle erstellten Projekte öffentlich
- Offizielle Website (englisch): https://glitch.com
- CodePen: Online-Entwicklungsumgebung mit ähnlichem Umfang und Einsatzmöglichkeiten wie Glitch, unterstützt allerdings nur jeweils eine einzelne HTML- und CSS-Datei pro Projekt
- Kosten: Freie Version mit eingeschränktem Funktionsumfang (alle erstellten Projekte öffentlich)
- Offizielle Website (englisch): https://codepen.io
- W3C Online-Validator für HTML-Dokumente: https://validator.w3.org
- W3C Online-Validator für CSS: https://jigsaw.w3.org/css-validator/it
- X-Ray Googles: Online-Tool zum Live-Inspizieren und Verändern von HTML-Seiten im Browser
- Entwickler: Mouse, ursprünglich Mozilla
- Link zum Online-Tool: https://x-ray-goggles.mouse.org
Modellierung
- Structorizer: Grafisches Tool zum Erstellen von Struktogrammen, Export u. a. in Python möglich1
- Entwickler: Robert Fisch
- Lizenz: Struktorizer-Lizenz (freie Software, Open Source)
- Offizielle Website: https://structorizer.fisch.lu
- Struktog.: Online-Editor zum Erstellen von Struktogrammen im Browser, Export u. a. in Python möglich möglich, auch als Offline-Version verfügbar (bei GitHub)
- Entwickler: Klaus Ramm, Thiemo Leonhardt (TU Dresden)
- Lizenz: MIT-Lizenz (Open Source)
- Projekt bei GitHub: https://gitlab.com/ddi-tu-dresden/cs-school-tools/struktog
- Link zum Online-Editor: https://dditools.inf.tu-dresden.de/struktog
- Draw.io/Diagrams.net: Grafisches Tool zum Erstellen von verschiedenen Diagrammtypen, u. a. UML-Diagramme, Flow Charts, ER-Diagramme, vereinfachte Klassen-/Sequenzdiagramme), Online- und Offline-Version (Draw.io Desktop) vorhanden
- Entwickler: David Benson, JGraph
- Lizenz: Apache 2
- Offizielle Website: https://www.diagrams.net
- Projekte bei GitHub: https://github.com/jgraph/drawio, https://github.com/jgraph/drawio-desktop (Offline-Tool)
Netzwerke und Internet
Simulation von Netzwerken
- Filius: Lernanwendung zum forschend-entdeckenden Lernen zum Thema Rechnernetzwerke
- Merkmale: Ermöglicht das Erstellen und Simulieren von kleineren Netzwerken mit verschiedenen Webdiensten
- Entwickler: Stefan Freischlad
- Lizenz: GPLv2/3
- Offizielle Website: https://www.lernsoftware-filius.de
- Begleitmaterial (Skripte, Übungsaufgaben): https://www.lernsoftware-filius.de/Begleitmaterial
Allgemeine Werkzeuge
Grafikprogramme
- GIMP: Freie Software zum Erstellen und Bearbeiten von Rastergrafiken
- Lizenz: GPL/LGPLv3
- Offizielle Website: https://www.gimp.org
- Inkscape: Freie Software zum Erstellen und Bearbeiten von Vektorgrafiken
- Lizenz: GPLv2
- Offizielle Website: https://inkscape.org
Texteditoren
- Atom: Frei verfügbarer Texteditor mit vielen Erweiterungen (u. a. für HTML/CSS, Programmierung in Python, verteilte Versionsverwaltung mit Git, gemeinsames Bearbeiten von Dokumenten)
- Entwickler: GitHub
- Lizenz: MIT-Lizenz (Open Source)
- Offizielle Website: https://atom.io
- Visual Studio Code: Frei verfügbarer Texteditor mit vielen Erweiterungen (siehe Atom)
- Entwickler: Microsoft
- Lizenz: MIT-Lizenz (Open Source)
- Offizielle Website: https://code.visualstudio.com
- Notepad++: Freier Texteditor für Windows, auch als portable Version verfügbar; weniger Erweiterungsmöglichkeiten als Atom/VS Code, dafür leichtgewichtiger und einfacher zu bedienen
- Entwickler: Don Ho
- Lizenz: GPLv3
- Offizielle Website: https://notepad-plus-plus.org
- HexEd.it: Browserbasierter Hex-Editor zum Bearbeiten und Inspizieren von Binärdateien im Hexadezimalformat
- Entwickler: Jens Duttke
- Lizenz: frei
- Link zum Online-Editor: https://hexed.it
Dateiverwaltung
- 7-Zip: Freie Software zur Datenkompression, unterstützt Verschlüsselung
- Entwickler: Igor Pavlov
- Lizenz: LGPL, 3-Klausel-BSD
- Offizielle Website: https://www.7-zip.de
-
setzt voraus, dass die Java Runtime Environment (JRE) Version 11 auf dem Rechner installiert ist ↩︎
Sekundarstufe II
7. Blick über die Informatik
8. Algorithmen
9. Grundlagen der Programmierung
9.1 Arithmetische Ausdrücke und Variablen
In Python können Zahlen als primitive Werte verwendet werden. Sie werden dabei automatisch in einer geeigneten Darstellung im Speicher abgelegt. Wie genau die Daten intern dargestellt werden, ist bei der Programmierung in der Regel irrelevant. Es genügt, vordefinierte Funktionen und Operationen zu kennen, mit denen wir Zahlen verarbeiten können.
Durch Verknüpfung mit Funktionen und Operationen entstehen komplexe Ausdrücke, die von Python automatisch ausgewertet werden. Die interaktive Python-Umgebung erlaubt es, beliebigen Python-Code in einem Terminal auszuführen, kann also auch dazu verwendet werden, arithmetische Ausdrücke auszuwerten.
>>> 3 + 4
7
Arithmetische Ausdrücke
Aus der Mathematik kennen wir Ausdrücke wie \(x^2+2y+1\) oder \((x+1)^2\), die auch Variablen enthalten können. Diese entstehen aus Basiselementen
- Konstanten (z. B. \(1\), \(2\) oder \(\pi\))
- Variablen (z.B. \(x\), \(y\))
und können durch Anwendung von Funktionen wie \(+\), \(-\), \(\cdot\) auf bereits existierende Ausdrücke gebildet werden. Diese Funktionen (auch Operatoren genannt) sind zweistellig, verknüpfen also zwei Ausdrücke zu einem neuen Ausdruck.
Auch der Ausdruck \(\frac{\sqrt{x^2+1}}{x}\) entsteht durch Anwendung unterschiedlicher Funktionen, allerdings ungewöhnlich notiert. Python erfordert eine einheitlichere Darstellung von Ausdrücken. Zum Beispiel müssen wir
x**2statt \(x^2\),math.sqrt(x)statt \(\sqrt{x}\) unda/bstatt \(\frac{a}{b}\)
schreiben. Den Ausdruck \(\frac{\sqrt{x^2+1}}{x}\) schreiben wir in Python also als math.sqrt(x**2+1)/x. Hierbei können wir durch festgelegte Präzedenzen (Punktrechnung vor Strichrechnung) auf Klammern verzichten. Schreiben wir stattdessen math.sqrt(x**(2+1))/x, so ergibt sich nicht der gleiche Ausdruck, da die Funktion ** stärker bindet als +.
Der größte Teil der Funktionalität von Python wird in Form von Modulen zur Verfügung gestellt, die man beim Programmieren explizit importieren muss, um sie verwenden zu können.
Die Funktion sqrt ist Teil des Moduls math und kann mit import math oder from math import sqrt importiert werden.
Im Folgenden werten wir beispielhaft einige arithmetische Ausdrücke in der Python-Umgebung aus:
>>> import math
>>> 3**2
9
>>> math.sqrt(25)
5.0
>>> 9/3
3.0
>>> math.sqrt(5**2-9)/4
1.0
Variablen und Zuweisungen
In der Mathematik können arithmetische Ausdrücke Variablen enthalten, die als Platzhalter für Werte (oder Ausdrücke) stehen.
Auch in Programmiersprachen können wir Variablen verwenden, wenn wir ihnen initial einen Wert zuweisen. Im weiteren Programmablauf können wir mit dem Variablenbezeichner den Wert referenzieren oder der Variablen einen neuen Wert zuweisen.
Als Beispiel für einen Ausdruck mit Variablen betrachten wir die Formel \(\pi \cdot r^2\) zur Bestimmung des Flächeninhalts eines Kreises mit gegebenem Radius \(r\).
In Python können wir diese Formel wie folgt schreiben:
>>> import math
>>> math.pi * r**2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'r' is not defined
Da wir der Variablen r jedoch noch keinen Wert zugewiesen
haben, liefert Python beim Versuch, die Formel auszuwerten, eine
Fehlermeldung. Durch Zuweisung verschiedener Werte an r
können wir den Flächeninhalt von Kreisen mit unterschiedlichen Radien berechnen.
>>> import math
>>> r = 2
>>> math.pi * r**2
12.566370614359172
>>> r = 4
>>> math.pi * r**2
50.26548245743669
Die Zeilen r = 2 und r = 4 sind anders als alles bisher eingegebene keine Ausdrücke, sondern Zuweisungen, also eine spezielle Form sogenannter Anweisungen oder Instruktionen. Anweisungen haben anders als Ausdrücke keinen Wert. Zuweisungen speichern den Wert des Ausdrucks rechts vom Gleichheitszeichen in der Variablen links vom Gleichheitszeichen.
Während in der Mathematik die Gleichung \(x = x + 1\) keine
Lösungen hat, ist die Zuweisung x = x + 1 durchaus üblich:
>>> x = 41
>>> x
41
>>> x = x + 1
>>> x
42
Sie weist der Variablen x den Wert x+1 zu, also ihren eigenen um eins erhöhten (alten) Wert.
9.2 Weitere primitive Datentypen
In Python können wir nicht nur arithmetische, sondern zum Beispiel auch logische Ausdrücke auswerten und solche, deren Wert eine Zeichenkette, also Text, ist.
Zeichenketten
Eine Zeichenkette (englisch: string) wird dazu in Anführungszeichen eingeschlossen. Mehrere Zeichenketten können mit dem
+- Operator aneinandergehängt werden.
>>> 'Hallo'
'Hallo'
>>> 'Welt'
'Welt'
>>> 'Hallo' + 'Welt'
'HalloWelt'
>>> 'Hallo' + ' ' + 'Welt'
'Hallo Welt'
>>> 'Hallo' + ' ' + 'Welt' + '!'
'Hallo Welt!'
Zahlen können wir mit der Funktion str() in Zeichenketten konvertieren. Auf diese Weise können wir Zeichenketten mit arithmetischen Ausdrücken kombinieren:
>>> str(42)
'42'
>>> str(17+4)
'21'
>>> str(17) + str(4)
'174'
>>> 'Die Antwort ist ' + str(2*(17+4))
=> 'Die Antwort ist 42'
Der Operator + wird also sowohl zur Addition von Zahlen als
auch zur Konkatenation von Zeichenketten verwendet. Beim
Versuch, + mit einer Zahl und einer Zeichenkette aufzurufen,
erhalten wir allerdings einen Fehler:
>>> '40' + 2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: can only concatenate str (not "int") to str
>>> 40 + '2'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'int' and 'str'
Die Fehlermeldungen deuten darauf hin, dass Zahlen und Zeichenketten nicht automatisch ineinander konvertiert werden, denn es ist unklar, ob als Ergebnis die Zahl 42 oder die Zeichenkette '402' herauskommen soll. Diese Unklarheit müssen wir durch explizite Konvertierung (mittels str()) aufklären. Wollen wir eine Zeichenkette, die eine Zahl enthält, in eine Zahl konvertieren, können wir int() (für Ganzzahlen, englisch integer) oder float() (für Dezimalbrüche bzw. Gleitkommazahlen, englisch floating point number) benutzen.
>>> int('40') + 2
42
>>> '40' + str(2)
'402'
>>> 40 + float('2')
42.0
Logische Ausdrücke
Logische Ausdrücke beschreiben Wahrheitswerte. Sie sind aus den Konstanten True und False aufgebaut, wobei komplexere Ausdrücke durch Anwendung logischer Operationen gebildet werden können. Eine Konjunktion (logisches “und”) wird durch den Operator and gebildet, eine Disjunktion (logisches “oder”) durch or und eine Negation (logisches “nicht”) durch ein vorangestelltes not. Hier sind einige Beispiele für logische Ausdrücke in der Python-Umgebung:
>>> True and False
False
>>> not False
True
>>> False or (True and not False)
True
Auch Vergleichsoperatoren haben logische Werte als Ergebnis. Zum Beispiel liefert der Ausdruck 3 < 4 das Ergebnis True. Hier sind weitere Beispiele für logische Ausdrücke mit Vergleichsoperatoren:
>>> 4 < 3
False
>>> 5+2 >= 6
True
>>> 5+2 >= 6+3
False
>>> 5+2 >= 6+3 or 3 <= 10/2
True
>>> 5+2 >= 6+3 or 3 <= 10/5
False
>>> 5+2 == 3+4
True
>>> 5+2 != 3+4
False
Nicht verwechseln! Ein einfaches Gleichheitszeichen = steht in Python für eine Wertzuweisung (z. B. x = 4). Für den Vergleich, ob zwei Werte identisch sind, muss ein doppeltes Gleichheitszeichen == verwendet werden:
>>> x = 4 # Wertzuweisung
>>> x == 4 # Vergleichsoperation
True
>>> x == 2+2
True
>>> 3 == 4
False
>>> 3 = 4
File "<stdin>", line 1
3 = 4
^
SyntaxError: cannot assign to literal
Variablen für Text und Wahrheitswerte
Auf rechten Seiten einer Zuweisung können beliebig komplizierte Ausdrücke stehen, deren Werte nicht unbedingt Zahlen zu sein brauchen.
>>> antwort = 2*(17+4)
>>> antwort
42
>>> text = 'Die Antwort ist ' + str(antwort)
>>> text
'Die Antwort ist 42'
>>> antwort = text == 'Die Antwort ist 42'
>>> antwort
True
Hier wird der Variablen antwort zunächst der Wert 42 zugewiesen und dieser dann zur Definition der Variablen text verwendet. Schließlich wird der Wert der Variablen antwort auf True geändert, indem ihr das Ergebnis eines Vergleiches zugewiesen wird.
9.2.1 Übungsaufgaben
Aufgaben
Aufgabe 1: Ausdrücke und Zuweisungen
Starten Sie die interaktive Python-Umgebung python in einem Terminal und bestimmen Sie den Wert ausgewählter Ausdrücke. Achten Sie dabei darauf, in welcher Reihenfolge komplexe Ausdrücke ausgewertet werden.
Verwenden Sie Zuweisungen, um den Wert von Teilausdrücken in einer Variablen zu speichern. Welche Vorteile hat die Definition von Variablen?
Aufgabe 2: Programme ergänzen
Ergänzen Sie in den im folgenden gezeigten Programmen jeweils die markierte Zeile darart, dass das Programm 42 ausgibt.
Hinweise:
- Die letzte Programmzeile der gezeigten Programme enthält jeweils eine
print()-Anweisung. Der Effekt einer solchen Anweisung ist, dass der Wert des Ausdrucks, der anprint()übergeben wird, in eine Zeichenkette umgewandelt und im Terminal ausgegeben wird. Zeichenketten werden dabei ohne Anführungszeichen ausgegeben. - Das
#-Zeichen ist ein Kommentarzeichen. Es bewirkt, dass alle folgenden Zeichen bis zum Zeilenende vom Python-Interpreter ignoriert werden.
a)
zahl = 41
zahl + 1 # diese Zeile ergänzen oder korrigieren
print(zahl)
b)
wort = "40"
# hier eine Zeile einfügen
print(int(wort) + zahl)
c)
wort = "2"
# hier eine Zeile einfügen
print(str(zahl) + wort)
d)
zahl = 41
zahl + 1 = zahl # diese Zeile ergänzen oder korrigieren
print(zahl)
e)
x = 6
x * 7 # diese Zeile ergänzen oder korrigieren
print(result)
f)
x = 6
s = str(5 * x)
ergebnis = s + 2*x # diese Zeile ergänzen oder korrigieren
print(ergebnis)
g)
zwei = 2
vierzig = 40
# hier eine Zeile einfügen
print(zwei + und + vierzig)
h)
zwei = "2"
vier = "4"
# hier eine Zeile einfügen
print(vier + zigund + zwei)
i)
a = 0
b = 1
c = a
d = a + b
# hier eine Zeile einfügen
f = d - e
print(a * 2**0 + b * 2**1 + c * 2**2 + d * 2**3 + e * 2**4 + f * 2**5)
j)
a = 1 + 3 + 5
b = a + 7 + 9 + 11
str(a + b - 1) # diese Zeile ergänzen oder korrigieren
print(value)
9.3 Bedingte Anweisungen
Nachdem wir im vorherigen Abschnitt Zuweisungen kennen gelernt haben, mit denen der Wert eines Ausdrucks in einer Variablen gespeichert werden kann, wenden wir uns nun einer weiteren Form der Anweisung zu. In bedingten Anweisungen ist die Ausführung einzelner Anweisungen vom Wert eines logischen Ausdrucks abhängig.
Die folgende Anweisung, in der das Schlüsselwort1 if vorkommt, demonstriert diese Idee:
if x < 0: x = -1 * x
Hier wird die Anweisung x = -1 * x nur dann ausgeführt, wenn der Wert des logischen Ausdrucks x < 0 gleich True ist, wenn also der Wert von x kleiner als 0 ist. Ist das nicht der Fall (ist also der Wert des logischen Ausdrucks x < 0 gleich False) dann wird die Zuweisung x = -1 * x nicht ausgeführt. In jedem Fall hat also nach der Ausführung der bedingten Anweisung die Variable x einen nicht-negativen Wert, nämlich den Absolutbetrag ihres ursprünglichen Wertes. Die folgenden Aufrufe demonstrieren die Auswertung dieser bedingten Anweisung:
>>> x = -4
>>> x
-4
>>> if x < 0: x = -1 * x
...
>>> x
4
>>> if x < 0: x = -1 * x
...
>>> x
4
In der interaktiven Python-Umgebung zeigt ... an, dass der if-Block noch nicht abgeschlossen ist und weitere Anweisungen als Teil des Blocks hinzugefügt werden können. Zur Beendung des if-Blocks muss Enter gedrückt werden.
Bedingte Anweisungen können auch Alternativen enthalten,
die ausgeführt werden, wenn die Bedingung nicht erfüllt ist.
Dazu verwenden wir das Schlüsselwort else wie im folgenden
Beispiel:
if x > y: z = x
else: z = y
Hier wird der Variablen z der Wert der Variablen x zugewiesen,
falls dieser größer ist als der Wert von y. Ist das nicht der Fall,
erhält z den Wert von y. In jedem Fall hat also die Variable z
nach dieser Anweisung den Wert des Maximums der Werte von x und y.
Die folgende Anweisungsfolge demonstriert die Auswertung einer solchen Berechnung:
>>> x = 4
>>> y = 5
>>> if x < y: z = x
... else: z = y
...
>>> z
5
Da der Wert des logischen Ausdrucks x > y gleich False ist, wird die Zuweisung z = y ausgeführt. Danach hat die Variable z also den Wert 5.
Bedingte Anweisungen mit Alternative werden Bedingte Verzweigungen genannt. Bedingte Anweisungen ohne Alternative heißen auch Optionale Anweisungen.
Statt Anweisungen in der interaktiven Python-Umgebung einzugeben, können wir sie auch in einer Textdatei speichern. Dabei können wir einzelne Anweisungen auf mehrere Zeilen verteilen, was der Lesbarkeit des Programms zugute kommt.
Wir können zum Beispiel das folgende Programm in einer
Datei max.py speichern.
x = 4
y = 5
if x > y:
z = x
else:
z = y
print(z)
Hier ist die bedingte Anweisung auf mehrere Zeilen verteilt und zusätzlich eingerückt. Dies dient nicht nur der besseren Lesbarkeit, sondern hat auch eine syntaktische Funktion. Mehr dazu im Absatz Einrückungen.
Die Ausgabe-Anweisung print(z) dient dazu, den Wert von z im Terminal auszugeben. Dies ist nötig, da wir das Programm nicht in einer interaktiven Umgebung, die Ergebnisse von Ausdrücken automatisch anzeigt, sondern mit dem Interpreter python auswerten. Dazu wechseln wir im Terminal in das Verzeichnis, in dem wir das Programm max.py gespeichert haben und führen es dann mit dem folgenden Kommando aus:
$ python max.py
5
Als letzter Schritt der Ausführung wird die Zahl 5 im Terminal ausgegeben.
Einrückungen
Anders als in vielen anderen Sprachen wird in Python ausschließlich über Einrückungen festgelegt, welche Anweisungen von einer Bedingung abhängen.
Betrachten wir die folgenden Beispiele:
if x < 0:
x = -1 * x
y = y + 1
und
if x < 0:
x = -1 * x
y = y + 1
Im ersten Fall wird die Anweisung y = y + 1 nur ausgeführt, falls der Ausdruck x < 0 zu True ausgewertet wird, im zweiten Fall wird y = y + 1 immer ausgeführt:
>>> x = -4
>>> y = 0
>>> if x < 0:
... x = -1 * x
... y = y + 1 # Diese Zeile ist abhängig von x < 0
...
>>> x
4
>>> y
1
>>> if x < 0:
... x = -1 * x
... y = y + 1 # Diese Zeile ist abhängig von x < 0
...
>>> x
4
>>> y
1
>>> if x < 0:
... x = -1 * x
...
>>> y = y + 1 # Diese Zeile ist NICHT abhängig von x < 0
>>> x
4
>>> y
2
Dies gilt insbesondere, wenn die bedingten Anweisungen ineinander geschachtelt sind – wenn also die Alternativen selbst auch wieder bedingte Anweisungen sind. Als Beispiel einer geschachtelten bedingten Anweisung betrachten wir das folgende Programm xor.py, das das Ergebnis der Exklusiv-Oder-Verknüpfung zweier Variablen ausgibt.
x = True
y = False
if x:
if y:
z = False
else:
z = True
else:
if y:
z = True
else:
z = False
print(str(x) + " xor " + str(y) + " = " + str(z))
Hier werden die logischen Ausdrücke x und y als Bedingungen für bedingte Anweisungen verwendet, wobei die zweite im
so genannten “then”-Zweig der ersten und die dritte im so genannten “else”-Zweig der ersten steht. Bei der Ausführung
dieses Programms wird das Ergebnis von True xor False ausgegeben.
$ python xor.py
True xor False = True
-
Schlüsselworte sind von einer Programmiersprache reservierte Namen mit besonderer Bedeutung. Sie dürfen daher nicht als Variablennamen verwendet werden. ↩︎
9.3.1 Übungsaufgaben
Hausaufgabe: Programme mit Bedingten Anweisungen
Schreiben Sie ein Python-Programm max3.py, das das Maximum dreier
Werte im Terminal ausgibt, die in den ersten drei Zeilen des Programms
den Variablen x, y, und z zugewiesen werden. Achten Sie auf korrekte Einrückungen. Testen Sie Ihre Implementierung mit geeigneten Werten.
Schreiben Sie Python-Programme not.py, and.py und or.py, die logische Negation, Konjunktion beziehungsweise Disjunktion von am Programmanfang zugewiesenen Variablen im Terminal ausgeben. Verwenden Sie dabei keine vordefinierten logischen Operationen sondern nur bedingte Anweisungen analog zum Programm für die exklusive Oder-Verknüpfung aus der Vorlesung. Definieren Sie ihre Programme so, dass Ausgaben der Form not false = true, true and false = false und true or false = true erzeugt werden. Testen Sie Ihre Implementierung mit allen möglichen Werten und protokollieren Sie dabei die Ausgabe Ihres Programms.
9.4 Schleifen
Neben bedingten Anweisungen gibt es in höheren Programmiersprachen auch Sprachkonstrukte zur wiederholten Ausführung von Anweisungen. Im folgenden werden zwei verschiedene solcher Konstrukte vorgestellt: die Zähl-Schleife und die bedingte Schleife.
Zähl-Schleifen
Eine Zähl-Schleife wiederholt eine Anweisung (oder einen Anweisungsblock), wobei eine Zählvariable einen festgelegten Zahlenbereich durchläuft. Die Anzahl der Wiederholungen ist also durch den definierten Zahlenbereich festgelegt. Als Beispiel für eine Zähl-Schleife schreiben wir ein Programm 1bis100.py, das die Zahlen von 1 bis 100 addiert:
sum = 0
for i in range(1, 101):
sum = sum + i
print(sum)
Hier sind for und in Schlüsselworte. Die so genannte Zählvariable i nimmt während der wiederholten Ausführung des so genannten Schleifenrumpfes sum = sum + i nacheinander die Werte von 1 bis 100 an, sodass in sum nach Ausführung der Wiederholung die Summe der Zahlen von 1 bis 100 gespeichert ist, die mit der letzten Anweisung ausgegeben wird. Der zweite Parameter der range-Funktion gibt den Wert an, der nicht mehr berücksichtigt werden soll.
$ python 1bis100.py
5050
Als Grenzen für den von der Zählvariable durchlaufenen Zahlenbereich können wir beliebige Ausdrücke verwenden, deren Wert eine Zahl ist – insbesondere auch Variablen, wie das folgende Beispiel zeigt:
n = 7
q = 0
for i in range(1,n+1):
u = 2*i - 1
q = q + u
print(str(n) + "zum Quadrat ist " + str(q))
Bei diesem Programm besteht der Rumpf der Wiederholung aus zwei Zuweisungen. Die erste definiert u als die i-te ungerade Zahl und die zweite addiert diese zur Variablen q hinzu. Nach Ausführung der Wiederholung ist in q also die Summe der ersten n ungeraden Zahlen gespeichert, also n zum Quadrat. Wenn wir dieses Programm in der Datei quadrat.py speichern und diese dann ausführen, erhalten wir die folgende Ausgabe:
$ python quadrat.py
7 zum Quadrat ist 49
Bedingte Schleifen
Sogenannte bedingte Schleifen sind ein weiteres Konstrukt höherer
Programmiersprachen zur Wiederholung von Anweisungen. Anders als bei
Zähl-Schleifen hängt die Anzahl der Wiederholungen bei einer
bedingten Schleife nicht von einem vorab definierten Zahlenbereich ab,
sondern von einem logischen Ausdruck, der vor jedem Schleifendurchlauf
ausgewertet wird. Ist der Wert dieser sogenannten Schleifenbedingung
gleich True, so wird der Rumpf (ein weiteres Mal) ausgeführt, ist er
gleich False, so wird die Ausführung der bedingten Schleife
beendet. Bei einer bedingten Schleife ist also nicht immer vorab klar,
wie oft der Schleifenrumpf ausgeführt wird, da der Wert der Bedingung
von Zuweisungen im Schleifenrumpf abhängen kann.
Als erstes Beispiel für eine bedingte Schleife berechnen wir wieder die Summe der Zahlen von 1 bis 100:
i = 0
sum = 0
while i < 100:
i = i + 1
sum = sum + i
print(sum)
Nach dem Schlüsselwort while steht die Schleifenbedingung, danach folgt der eingerückte Schleifenrumpf. Anders als mit der Zähl-Schleife müssen wir hier den Wert der Zählvariable i explizit setzen, da bedingte Schleifen keine eingebaute Zählvariable haben. Falls i bei der Prüfung der Schleifenbedingung nicht mehr kleiner 100 ist, wird die Schleife beendet und die Summe der ersten 100 Zahlen ausgegeben.
In diesem Beispiel ist die Anzahl der Schleifendurchläufe einfach ersichtlich, da die Schleifenbedingung nur von dem Wert der Variablen i abhangt, die in jedem Schleifendurchlauf um eins erhöht wird. Im folgenden Programm ist die Anzahl der Schleifendurchläufe nicht so einfach ersichtlich.:
n = 144
i = 0
q = 0
while q < n:
i = i + 1
q = q + 2*i - 1
print(i)
Hier wird in jedem Durchlauf die Zählvariable i um eins
erhöht und (wie beim Programm quadrat.py) der Variablen q
die i-te ungerade Zahl hinzuaddiert. Die Schleife wird ausgeführt, solange der Wert von q kleiner als n ist. Sie bricht also
ab, sobald q größer oder gleich n ist.
Wie im Programm quadrat.py ist nach jedem Schleifendurchlauf q = i*i. Das obige Programm gibt also die kleinste
Zahl i aus, deren Quadrat größer oder gleich n ist. Ist n eine
Quadratzahl, so ist die Ausgabe des Programms deren Quadratwurzel.
$ python wurzel.py
12
Bei der Programmierung mit bedingten Schleifen ist Vorsicht geboten, da nicht sichergestellt ist, dass die Schleifenbedingung irgendwann nicht mehr erfüllt ist. In diesem Fall bricht die Schleife nie ab, läuft also (potentiell) endlos weiter.
Eine einfache Endsloswiederholung können wir wie folgt definieren:
while True:
print("hi!")
Da diese Schleife nie beendet wird, werden nach ihr folgende Anweisungen nie ausgeführt. Eine häufige Fehlerquelle sind Zählvariablen, die wir vergessen im Rumpf zu erhöhen. Auch das folgende Programm terminiert also nicht:
i = 0
sum = 0
while i < 100:
sum = sum + i
Um versehentliche Nicht-Terminierung von vornherein auszuschließen sollten Sie, wenn möglich, Zähl-Schleifen verwenden. Nur wenn die Anzahl der Schleifendurchläufe nicht (einfach) ersichtlich ist, sollten Sie auf bedingte Schleifen zurückgreifen.
9.4.1 Übungsaufgaben
Aufgabe: Fakultäts-Berechnung mit Schleifen
Die Fakultät einer Zahl n ist definiert als das Produkt der Zahlen
von 1 bis n. Schreiben Sie ein Programm fakultaet.py, das die
Fakultät einer am Programmanfang zugewiesenen Variablen n
ausgibt. Berechnen Sie das Ergebnis einmal mit einer for-Schleife
und einmal mit einer while-Schleife. Vergleichen Sie die beiden
Implementierungen. Welche bevorzugen Sie? Begründen Sie Ihre Antwort.
Hausaufgabe: Fachsprache zur Beschreibung von Programmen
Benennen Sie im folgenden Programm alle Programmkonstrukte mit ihrem korrekten Namen. Benennen Sie insbesondere alle Anweisungen und alle Ausdrücke und geben Sie dabei auch die Teilausdrücke komplexer Ausdrücke an.
text = "Ho"
zahl = 3
for i in range(1,zahl+1):
if i % 2 == 1:
text = text + text
print(text)
Beschreiben Sie den Ablauf des Programms umgangsprachlich und geben Sie an, was es ausgibt.
Bonusaufgabe: Zählschleifen untersuchen
Ergründen Sie experimentell, wie sich for-Schleifen in Python verhalten, wenn im Schleifenrumpf Zuweisungen an die Zählvariable enthalten sind. Welche Werte hat die Zahlvariable jeweils vor einer solchen Zuweisung? Können Sie mit Hilfe von Zuweisungen an die Zählvariable eine nicht terminierende for-Schleife schreiben?
Bonusaufgabe: Python-Programm, das sich selbst ausgibt
Schreiben Sie ein nicht leeres Python-Programm, das, wenn es ausgeführt wird, seinen eigenen Quelltext im Terminal ausgibt. Verwenden Sie nur Python-Sprachkonstrukte, die bisher in der Vorlesung besprochen wurden.
Hinweise:
- Diese Bonus-Aufgabe ist sehr schwer. Selbst die Übungsgruppenleiter dürften Schwierigkeiten haben, sie zu lösen. Bei Detailfragen können sie aber trotzdem helfen.
- Alle Lösungen aus dem Internet, die ich gefunden habe, verwenden Sprachkonstrukte, die wir noch nicht besprochen haben und die sich nicht ohne Weiteres mit unseren Mitteln ausdrücken lassen.
- Zeilenumbrüche können in Python gelegentlich weggelassen (oder durch Semikolons ersetzt) werden.
- Zeichenketten können entweder in einfache oder in doppelte Hochkommata eingeschlossen werden. Dies ist nützlich, um Zeichenketten, die Hochkommata enthalten, zu definieren. Zum Beispiel ist
"'"eine Zeichenkette, die ein einfaches Kochkomma enthält und'"'eine Zeichenkette, die ein doppeltes Hochkomma enthält.
9.5 Programmablaufplan (PAP)
Zur Visualisierung einer Programmstruktur erstellt man einen Programmablaufplan (PAP). Ein PAP ist ein gerichteter Graph, dessen Knoten Anweisungen und Verzweigungen repräsentieren, die gerichteten Kanten zeigen auf die im Ablauf folgenden Elemente.
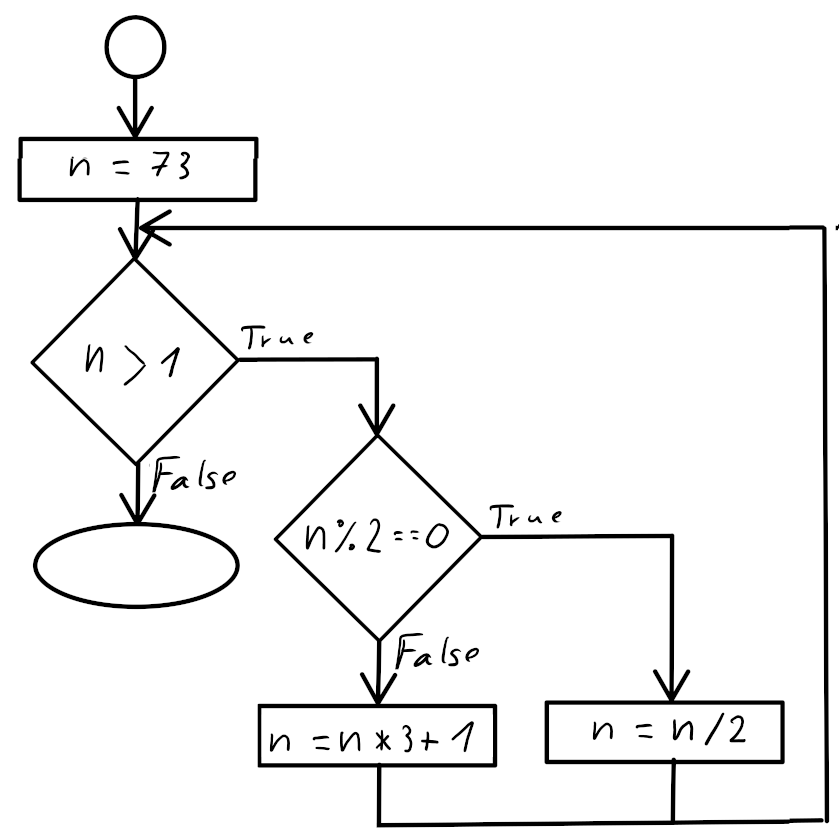
Die graphischen Elemente entsprechen denen von Flussdiagrammen.
| Element | Symbol |
|---|---|
| Start |  |
| Anweisung |  |
| Verzweigung mit Bedingung |  |
| Stop |  |
Mithilfe dieser Elemente lässt sich jedes Python-Programm als PAP visualisieren. Umgekehrt lässt sich nicht jeder PAP in ein Python-Programm überführen, da imperative Programmiersprachen bestimmte Restriktionen hinsichtlich des Kontrollflusses haben.
Zur Überführung eines Python-Programms in einen PAP werden Anweisungen in Rechtecke geschrieben.
Bedingte Anweisungen / Alternativen und Schleifen werden mithilfe von Verzweigungen dargestellt, wobei die Bedingungen als boolscher Ausdruck in die Raute geschrieben werden. Der True-Fall sollte nach rechts, der False-Fall nach unten abgeleitet werden, um Überschneidungen von Kanten zu vermeiden.
| Element | Symbol |
|---|---|
| Bedingte Anweisung | 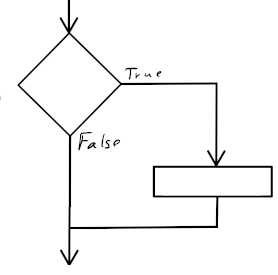 |
| Bedingte Alternative | 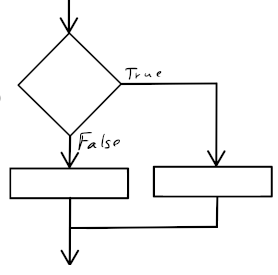 |
| Bedingte Schleife | 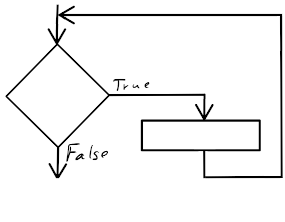 |
Verzweigungen dürfen nicht irgendwo hinführen.
- Eine Bedingte Anweisung / Alternative mündet in einen gemeinsamen Ausgang.
- Schleifen haben eine Rückführung aus dem Schleifenrumpf zur Schleifenbedingung.
- Andere Rückbezüge sind nicht erlaubt.
Ältere imperative Programmiersprachen (z. B. Basic) konnten mithilfe einer goto-Anweisung an eine beliebige Stelle des Programms springen. Moderne Programmiersprachen verbieten solche Sprünge. Damit wird eine besser lesbare Struktur erzwungen ohne Einbußen in der Mächtigkeit der Sprache.
9.5.1 Übungsaufgaben
Aufgabe: PAP in Python-Programm überführen
- Überführen Sie den PAP aus dem Skriptin ein lauffähiges Python-Programm.
- Testen Sie das Programm mit verschiedenen Werten für n und ermitteln Sie, ob das Programm jeweils terminiert.
- Analysieren Sie, ob das Programm unter kritischen Bedingungen (z. B. bei Wahl eines bestimmten Wertes für n) nicht terminieren könnte.
Aufgabe: PAP aus Python-Programm erstellen
Erstellen Sie einen PAP aus dem folgenden Python-Programm:
min = 1
max = 100
geheim = 37
erraten = False
while not erraten:
kandidat = (min + max) // 2
print("Ist die Zahl gleich " + str(kandidat) + "?")
if geheim == kandidat:
print("Ja, erraten.")
erraten = True
if geheim < kandidat:
print("Nein, meine Zahl ist kleiner!")
max = kandidat - 1
if geheim > kandidat:
print("Nein, meine Zahl ist größer!")
min = kandidat + 1
9.6 Tabellarische Programmausführung
In diesem Abschnitt lernen wir eine systematische Methode kennen, die Ausführung eines Programms zu dokumentieren. Sich im Kopf zu überlegen, welche Variablen wann mit welchen Werten belegt sind, wird bei größeren Programmen schnell unübersichtlich. Übersichtlicher ist eine tabellarische Notation, die zeilenweise festhält, wie sich die Werte von Variablen schrittweise verändern.
Um verschiedene Positionen in einem Programm zu benennen, schreiben wir hinter jede Anweisung einen Kommentar mit einer fortlaufenden Nummer. Auch die Bedingung in bedingten Anweisungen und bedingten Wiederholungen benennen wir mit solchen sogenannten Programmpunkten.
Das folgende Programm zur Berechnung des Absolutbetrags des Wertes einer Variablen x ist mit Programmpunkten annotiert.
x = -4 #1
if x < 0: #2
x = -1*x #3
Die folgende Tabelle demonstriert die Ausführung dieses Programms:
| Programmpunkt (PP) | x |
x < 0 |
|---|---|---|
| #1 | -4 | |
| #2 | True |
|
| #3 | 4 |
Jede Zeile der Tabelle beschreibt Werte von Variablen oder
Bedingungen an einem bestimmten Programmpunkt. Der Wert
von x ändert sich zweimal, der Wert der Bedingung x < 0 wird
einmal ausgewertet.
Die Programmpunkte eines Programms werden nicht immer in ihrer textuellen Reihenfolge durchlaufen. Beim Programm zur Berechnung des Maximums zweier Zahlen wird zum Beispiel eine Zuweisung übersprungen.
x = 4 #1
y = 5 #2
if x > y: #3
z = x #4
else:
z = y #5
print(z) #6
Die folgende Tabelle dokumentiert die Ausführung dieses Programms:
| PP | x |
y |
z |
x > y |
Ausgabe |
|---|---|---|---|---|---|
| #1 | 4 | ||||
| #2 | 5 | ||||
| #3 | False |
||||
| #5 | 5 | ||||
| #6 | 5 |
Hier wird der Programmpunkt #4 im if-Zweig der bedingten Anweisung übersprungen, weil die Bedingung x > y nicht erfüllt ist. Neben den verwendeten Variablen und Bedingungen dokumentiert diese Tabelle auch die Ausgaben mit print im Terminal.
Interessant werden solche Tabellen besonders, wenn Anweisungen durch Schleifen wiederholt werden. Auch die Deklaration einer Wiederholung mit fester Anzahl bekommt dabei eine eigene Nummer, um die Werte der Zählvariable zu protokollieren.
Hier ist ein Programm, angereichert mit Programmpunkten, zur Berechnung der Summe der ersten drei Zahlen:
sum = 0 #1
for i in range(1,4): #2
sum = sum + i #3
print(sum) #4
Die folgende Tabelle protokolliert dessen Ausführung:
| PP | sum |
i |
Ausgabe |
|---|---|---|---|
| #1 | 0 | ||
| #2 | 1 | ||
| #3 | 1 | ||
| #2 | 2 | ||
| #3 | 3 | ||
| #2 | 3 | ||
| #3 | 6 | ||
| #4 | 6 |
Hier werden die Programmpunkte #2 und #3 dreimal hintereinander durchlaufen, wobei die sich ändernden Werte der Variablen i und sum protokolliert werden.
Schließlich dokumentieren wir noch die Berechnung der Wurzel aus neun als Beispiel eines Programms mit bedingter Schleife.
n = 9 #1
i = 0 #2
q = 0 #3
while q < n: #4
i = i + 1 #5
q = q + 2*i - 1 #6
print(i) #7
Die folgende Tabelle zeigt, wie es zur der Ausgabe 3 am Ende
des Programms kommt:
| PP | n |
i |
q |
q < n |
Ausgabe |
|---|---|---|---|---|---|
| #1 | 9 | ||||
| #2 | 0 | ||||
| #3 | 0 | ||||
| #4 | True |
||||
| #5 | 1 | ||||
| #6 | 1 | ||||
| #4 | True |
||||
| #5 | 2 | ||||
| #6 | 4 | ||||
| #4 | True |
||||
| #5 | 3 | ||||
| #6 | 9 | ||||
| #4 | False |
||||
| #7 | 3 |
Hier werden die Programmpunkte #4, #5 und #6 dreimal durchlaufen. Es
wird deutlich, dass vor und nach jedem Schleifendurchlauf der Wert der
Variablen q gleich dem Quadrat des Wertes von i ist. Eine solche
Bedingung, die sich durch die Ausführung des Schleifenrumpfes nicht
verändert, heißt Schleifen-Invariante. Sie hilft uns zu erkennen, dass
die Ausgabe des Programms die Quadratwurzel von q ist. Ist n eine
Quadratzahl, so ist bei Programmende q gleich n, die Ausgabe also
die Quadratwurzel von n.
9.6.1 Übungsaufgaben
Aufgabe: Schleifenbedingungen mit Fließkommazahlen
- Dokumentieren Sie die beabsichtigte Ausführung des folgenden Programms mit einer Programmausführungstabelle und vergleichen Sie mit dem tatsächlichen Ablauf.
x = 0.0 #1
while x != 1.0: #2
print(x) #3
x = x + 0.1 #4
-
Ändern Sie die Schleifenbedingung so ab, dass das Programm (in Python) terminiert.
-
Schreiben Sie ein Programm, dass nacheinandner die Zahlen
0.0,0.1, und so weiter bis0.9ausgibt.
9.7 Zusammenfassung, Quellen und Lesetipps
Schlüsselwörter
| Schlüsselwort | Verwendung | Erläuterung |
|---|---|---|
import |
import Bibliothek |
Importiert die angegebene Bibliothek |
True |
Einer der beiden Werte, die ein logischer Ausdruck annehmen kann. | |
False |
Der andere der beiden Werte, die ein logischer Ausdruck annehmen kann. | |
and |
Logischer Ausdruck 1 and Logischer Ausdruck 2 |
Ergibt True, wenn sowohl Logischer Ausdruck 1 als auch Logischer Ausdruck 2 True sind. |
or |
Logischer Ausdruck 1 or Logischer Ausdruck 2 |
Ergibt True, wenn Logischer Ausdruck 1 und/oder Logischer Ausdruck 2 True sind. |
not |
not Logischer Ausdruck |
Verkehrt den Logischen Ausdruck ins Gegenteil |
if |
if Logischer Ausdruck: Anweisungen |
Führt die Anweisungen nur aus, wenn der Logische Ausdruck True ist. |
else |
if Logischer Ausdruck: Anweisungen else: Andere Anweisungen |
Nur in Verbindung mit if zu benutzen. Für den Fall, dass der Logische Ausdruck False ist, werden Andere Anweisungen ausgeführt. |
for |
for Variable in Liste: Anweisungen |
Führt die Anweisungen für jedes Element in der Liste aus. Die Listenelemente werden dabei jeweils durch die Variable adressiert. |
while |
while Logischer Ausdruck: Anweisungen |
Führt die Anweisungen aus, solange wie der Logische Ausdruck True ist. |
pass |
Tut nichts. |
Funktionen und Prozeduren
| Funktion | Erläuterung |
|---|---|
math.sqrt(x) |
Berechnet \(\sqrt{x}\) |
str(zahl) |
Wandelt die zahl in eine Zeichenkette um |
int(zeichenkette) |
Wandelt die zeichenkette in eine Ganzzahl um |
float(zeichenkette) |
Wandelt die zeichenkette in eine Kommazahl um |
print(text) |
Gibt den text auf der Konsole aus |
range(start, ende, schrittweite) |
Erzeugt eine Liste von Zahlen, die bei startbeginnt, vor dem ende aufhört, jeweils im Abstand von schrittweite |
Quellen und Lesetipps
- Offizielle Python-Dokumentation
- Edsger W. Dijkstra: A Case Against The GOTO Statement
- Deutschsprachiges Python-Tutorial
9.8 Lösungen
Lösungen
Aufgabe: Ausdrücke und Zuweisungen
In Python gibt es unterschiedliche Arten von Werten, die man sich in der interaktiven Python-Umgebung anzeigen lassen kann.
>>> "Hallo"
'Hallo'
>>> "Hallo" + " " + "Python" + "!"
'Hallo Python!'
>>> 6*(3+4)
42
>>> 42 / 6
7.0
>>> 45 / 6
7.5
>>> 45 % 6
3
>>> 6 * 7 == 42
True
>>> 1 > 2
False
>>> True and not False
True
>>> 6 * 7 == 42 or 1 > 2
True
>>> str(42)
'42'
>>> str(6 * 7) == 42
False
>>> int(42)
42
>>> int("6 * 7")
6
Der Divisions-Operator (/) liefert als Ergebnis eine Fließkommazahl. Der Divisions-Operator (//) beschreibt eine ganzzahlige Division und liefert als Ergebnis eine Ganzzahl. Der Rest einer ganzzahlige Division wird mit dem Modulo-Operator (%) ermittelt
>>> 5//3
1
>>> 5%3
2
>>> 1/4
0.25
>>> 1.0/4
0.25
>>> 1/4.0
0.25
>>> 1.0/4.0
0.25
Die im Folgenden verwendeten arithmetischen Ausdrücke werden bei fehlender Klammerung linksassoziativ ausgewertet:
>>> 1-2-3
-4
>>> 1-(2-3)
2
>>> (1-2)-3
-4
>>>45/6/2
3.75
>>>45/(6/2)
15.0
>>> (45/6)/2
3.75
Potenzierung bindet stärker als Multiplikation und Division:
>>> 2*3**4
162
>>> 2*(3**4)
162
>>> (2*3)**4
1296
>>> 128/2**3
16.0
>>> 128/(2**3)
16.0
>>> (128/2)**3
262144.0
Durch Zuweisungen lassen sich Werte in Variablen speichern. Es gibt auch vordefinierte Werte.
import math
>>> text = "Hallo"
>>> text + text + text
"HalloHalloHallo"
>>> math.pi
3.141592653589793
>>> radius = 3
>>> umfang = 2 * math.pi * radius
>>> umfang
18.84955592153876
Aufgabe: Programme ergänzen
Hier sind ergänzte Varianten der gezeigten Programme:
a)
zahl = 41
zahl = zahl + 1 # diese Zeile ergänzen oder korrigieren
print(zahl)
b)
wort = "40"
zahl = 2 # hier eine Zeile einfügen
print(int(wort) + zahl)
c)
wort = "2"
zahl = 4 # hier eine Zeile einfügen
print(str(zahl) + wort)
d)
zahl = 41
zahl = zahl + 1 # diese Zeile ergänzen oder korrigieren
print(zahl)
e)
x = 6
result = x * 7 # diese Zeile ergänzen oder korrigieren
print(result)
f)
x = 6
s = str(5 * x)
ergebnis = int(s) + 2*x # diese Zeile ergänzen oder korrigieren
print(ergebnis)
g)
zwei = 2
vierzig = 40
und = 0 # hier eine Zeile einfügen
print(zwei + und + vierzig)
h)
zwei = "2"
vier = "4"
zigund = "" # hier eine Zeile einfügen
print(vier + zigund + zwei)
i)
a = 0
b = 1
c = a
d = a + b
e = 0 # hier eine Zeile einfügen
f = d - e
print(a * 2**0 + b * 2**1 + c * 2**2 + d * 2**3 + e * 2**4 + f * 2**5)
j)
a = 1 + 3 + 5
b = a + 7 + 9 + 11
value = a + b - 3 # diese Zeile ergänzen oder korrigieren
print(value)
Hausaufgabe: Programme mit Bedingten Anweisungen
Das Programm max3.py zur Berechnung des Maximums dreier Zahlen
verwendet geschachtelte Bedingte Anweisungen.
x = 3
y = 4
z = 1
if x > y:
if x > z:
m = x
else: # y < x <= z
m = z
else: # x <= y
if y > z:
m = y
else:
m = z # x <= y <= z
print("max(" + str(x) + "," + str(y) + "," + str(z) + ") = " + str(m))
Hier sind einige Beispielausgaben.
max(1,2,3) = 3
max(1,1,1) = 1
max(2,2,1) = 2
max(3,2,1) = 3
max(3,4,1) = 4
Die geschachtelten Bedingte Verzweigungen könnten alternativ durch die folgenden Anweisungen ersetzt werden, ohne die Ausgabe des Programms zu verändern:
m = x
if m < y:
m = y
if m < z:
m = z
Die Programme not.py, and.py und or.py lassen sich jeweils mit
einer einzigen bedingten Anweisung definieren. Hier ist die Definition
von not.py mit Ausgaben für alle möglichen Eingaben.
x = False
if x:
z = False
else:
z = True
print("not " + str(x) + " = " + str(z))
# not False = True
# not True = False
Hier ist die Definition von and.py mit Ausgaben für alle möglichen
Eingaben.
x = True
y = True
if x:
z = y
else:
z = False
print(str(x) + " and " + str(y) + " = " + str(z))
# False and False = False
# False and True = False
# True and False = False
# True and True = True
Hier ist die Definition von or.py mit Ausgaben für alle möglichen
Eingaben.
x = True
y = True
if x:
z = True
else:
z = y
print(str(x) + " or " + str(y) + " = " + str(z))
# False or False = False
# False or True = True
# True or False = True
# True or True = True
Aufgabe: Fakultäts-Berechnung mit Schleifen
Das folgende Programm berechnet die Fakultät einmal mit einer
for-Schleife und einmal mit einer while-Schleife.
n = 10
f = 1
for i in range(1,n+1):
f = f * i
print(f)
f = 1
i = 0
while i < n:
i = i + 1
f = f * i
print(f)
Die Version mit der for-Schleife ist kürzer, wegen der automatischen
Berechnung der Zählvariable weniger fehleranfällig und sicher
terminierend. Das Programm mit der while-Schleife würde ein falsches
Ergebnis berechnen, wenn wir die Zählvariable am Ende des
Schleifenrumpfes hochzählen würden. Es würde nicht terminieren, wenn
wir das Hochzählen vergessen hätten.
Hausaufgabe: Fachsprache zur Beschreibung von Programmen
Das Programm enthält drei Variablen: text, zahl und i. Die Variable i ist die Zählvariable der Zählschleife. Die ersten beiden Zeilen enthalten Zuweisungen an die Variablen text und zahl. Die zugewiesenen Werte sind "Ho" und 3. Beides sind primitive Ausdrücke, die also nicht weiter ausgerechnet werden müssen. "Ho" ist eine Zeichenkette und 3 ist eine Zahl. Eine weitere Zuweisung steht im then-Zweig der optionalen Anweisung
im Rumpf der Zählschleife. Hier wird der Variablen text der Wert des Ausdrucks text + text zugewiesen. Letzterer ist ein komplexer Ausdruck, in dem zweimal die Variable text als Teilausdruck vorkommt. Die Bedingung der optionalen Anweisung i % 2 == 1 ist ebenfalls ein komplexer Ausdruck und zwar ein logischer.
Sie enthält die Teilausdrücke i % 2, i, 2 und 1. Die erste Zeile der Zählschleife enthält die arithmetischen Ausdrücke 1 und zahl zur Definition der Grenzen des Bereiches, den die Zählvariable durchläuft. Die letzte Programmzeile enthält eine Ausgabe-Anweisung, die den Wert der Variablen text ausgibt.
Der Rumpf der Zählschleife wird dreimal durchlaufen. Die Bedingung der optionalen Anweisung ist genau dann True, wenn i = 1 oder i = 3 gilt. Die Zuweisung text = text + text wird also zweimal ausgeführt. Nach dem ersten Mal erhält die Variable text den Wert "HoHo", nach dem zweiten Mal den Wert "HoHoHoHo". Die Ausgabe des Programms ist also HoHoHoHo.
Bonusaufgabe: Zählschleifen untersuchen
Es ist in Python nicht möglich, mit einer for-Schleife eine Endlosschleife zu programmieren. Selbst wenn der Schleifenrumpf Zuweisungen an die Zählvariable enthält, wirkt diese sich nur bis zum Ende des Schleifenrumpfes aus. Im nächsten Durchlauf hat die Zählvariable unabhängig von Zuweisungen den nächsten Wert im Zahlenbereich. Auch Zuweisungen an eine zur Definition des Zahlenbereiches verwendete Variable im Schleifenrumpf ändern den durchlaufenen Bereich nicht. Das folgende Programm veranschaulicht dieses Verhalten.
n = 3
for i in range(1,n+1):
print("Wert von i vor der Zuweisung: " + str(i))
i = i - 1
print("Wert von i nach der Zuweisung: " + str(i))
n = n + 1
Ausgabe dieses Programms:
Wert von i vor der Zuweisung: 1
Wert von i nach der Zuweisung: 0
Wert von i vor der Zuweisung: 2
Wert von i nach der Zuweisung: 1
Wert von i vor der Zuweisung: 3
Wert von i nach der Zuweisung: 2
Bonusaufgabe: Python-Programm, das sich selbst ausgibt
Das folgende Python-Programm erzeugt sich selbst als Ausgabe.
q = '"'
r = "'"
s = "print('q = '+r+q+r); print('r = '+q+r+q); print('s = '+q+s+q); print(s)"
print('q = '+r+q+r); print('r = '+q+r+q); print('s = '+q+s+q); print(s)
Die letzte Programmzeile enthält vier Ausgabe-Anweisungen. Jede dieser Anweisungen gibt eine Zeile des Programms aus.
Der Wert, der in der dritten Programmzeile der Variablen s zugewiesen wird, entspricht der vierten Programmzeile. Die Variable s wird deshalb sowohl für die dritte als auch für die vierte Ausgabe-Anweisung verwendet. Die Zuweisungen an die Variablen q und r helfen dabei, die richtigen Hochkommata in der Ausgabe zu erzeugen.
Ein Programm, das sich selbst als Ausgabe erzeugt, heißt “Quine” - in Anlehnung an Quine’s Paradox:
“Yields Falsehood when preceded by its quotation” yields Falsehood when preceded by its quotation.
Aufgabe: Schleifenbedingungen mit Fließkommazahlen
| PP | x | x != 1 | Ausgabe |
|---|---|---|---|
| #1 | 0.0 | ||
| #2 | True | ||
| #3 | 0.0 | ||
| #4 | 0.1 | ||
| #2 | True | ||
| #3 | 0.1 | ||
| #4 | 0.2 | ||
| #2 | True | ||
| #3 | 0.2 | ||
| #4 | 0.3 | ||
| #2 | True | ||
| #3 | 0.3 | ||
| #4 | 0.4 | ||
| #2 | True | ||
| #3 | 0.4 | ||
| #4 | 0.5 | ||
| #2 | True | ||
| #3 | 0.5 | ||
| #4 | 0.6 | ||
| #2 | True | ||
| #3 | 0.6 | ||
| #4 | 0.7 | ||
| #2 | True | ||
| #3 | 0.7 | ||
| #4 | 0.8 | ||
| #2 | True | ||
| #3 | 0.8 | ||
| #4 | 0.9 | ||
| #2 | True | ||
| #3 | 0.9 | ||
| #4 | 1.0 | ||
| #2 | False |
In Python terminiert das gegebene Programm nicht, da aufgrund von Rundungsfehlern, stets x != 1.0 gilt. Wir korrigieren es, indem wir die Schleifenbedingung wie folgt anpassen.
x = 0.0 #1
while x < 1.0: #2
print(x) #3
x = x + 0.1 #4
Auch dieses Programm liefert allerdings noch nicht die gewünschte Ausgabe.
0.0
0.1
0.2
0.30000000000000004
0.4
0.5
0.6
0.7
0.7999999999999999
0.8999999999999999
0.9999999999999999
Das folgende Programm behebt dieses Problem.
for i in range(0,10):
print(i/10)
10. Programmiertechniken
10.1 Aufzählen und Überprüfen
Ein Vorteil eines Computers gegenüber einem Menschen ist die Fähigkeit, viele Werte sehr schnell aufzählen und gewisse Eigenschaften für diese Werte testen zu können. Somit können viele Probleme, bei denen der Bereich der möglichen Lösungen endlich ist und aufgezählt werden kann, mit der Programmiertechnik Aufzählen und Überprüfen gelöst werden.
Als Beispiel für diese Technik betrachten wir die Berechnung des größten gemeinsamen Teilers zweier natürlicher Zahlen. Der größte gemeinsame Teiler zweier Zahlen wird z.B. beim Kürzen von Brüchen verwendet, wobei Zähler und Nenner durch ihren größten gemeinsamen Teiler dividiert werden.
Mathematisch kann der größte gemeinsame Teiler (ggT) wie folgt definiert werden. Für gegebene natürliche Zahlen \(a, b \in \mathbb{N}\) ist ((ggT(a,b) = c \in \mathbb{N}\) diejenige natürliche Zahl für die gilt: c teilt a ohne Rest, c teilt b ohne Rest und für alle weiteren Teiler d von a und b gilt \(c > d\).
Als Beispiel betrachten wir folgende Zahlen.
- 21 hat die Teiler 1,3,7 und 21.
- 18 hat die Teiler 1,2,3,6,9 und 18.
Der größte gemeinsame Teiler von 21 und 18 ist also \(ggT(21,18) = 3\).
Jede positive Zahl ist ein Teiler der Null. Für alle \(a > 0\) gilt also \(ggT(a,0) = ggT(0,a) = a\). Der Wert von \(ggT(0,0)\) ist nicht definiert, da alle positiven Zahlen Teiler von 0 sind; es gibt also keinen größten gemeinsamen Teiler.
Für die Überprüfung, ob eine Zahl eine andere ohne Rest teilt kann der
Modulo-Operator verwendet werden, welcher den Rest einer ganzzahligen
Division liefert. Falls a und b ganzzahlige Werte sind, so liefert
% den Rest der ganzzahligen Division von a durch b.
Wie können wir das Problem der Berechnung größter gemeinsamer Teiler algorithmisch lösen? Eine einfache Methode ist die Berechnung durch Aufzählen und Überprüfen.1
Der ggT von a und b liegt sicherlich zwischen 1 und der kleineren der beiden Zahlen. Wir können also diese Werte der Reihe nach aufzählen und jeweils testen, ob die entsprechende Zahl beide gegebenen Zahlen ohne Rest teilt.
Für die Überprüfung, ob eine Zahl eine andere ohne Rest teilt kann der
Modulo-Operator verwendet werden, welcher den Rest einer ganzzahligen
Division liefert. Falls a und b ganzzahlige Werte sind, so liefert
% den Rest der ganzzahligen Division von a durch b.
Das folgende Programm berechnet zunächst das Minimum min gegebener
Zahlen a und b und sucht dann in einer Zähl-Schleife den größten
gemeinsamen Teiler dieser Zahlen.
a = 4 #1
b = 6 #2
if a < b: #3
min = a #4
else:
min = b #5
for i in range(1,min+1): #6
if a%i == 0 and b%i == 0: #7
ggT = i #8
print(ggT) #9
Wir verwenden eine Zähl-Schleife, da wir alle Werte zwischen 1 und
min daraufhin testen wollen, ob sie ein Teiler von sowohl a als
auch b sind. Wir wissen also vorher, wieviele Schleifendurchläufe
dafür gebraucht werden. Die Bedingung für den Test ist wegen der
Präzedenzen der beteiligten Operatoren so geklammert:
((a%i) == 0) and ((b%i) == 0).
Bei Programmende ist die größte Zahl i, die diese
Bedingung erfüllt (also der ggT von a und b) in der Variablen
ggT gespeichert.
Die folgende Tabelle dokumentiert die Ausführung dieses Programms.
| PP | a | b | a < b | min | i | a%i == 0 and b%i == 0 | ggT | Ausgabe |
|---|---|---|---|---|---|---|---|---|
| #1 | 4 | |||||||
| #2 | 6 | |||||||
| #3 | True | |||||||
| #4 | 4 | |||||||
| #6 | 1 | |||||||
| #7 | True | |||||||
| #8 | 1 | |||||||
| #6 | 2 | |||||||
| #7 | True | |||||||
| #8 | 2 | |||||||
| #6 | 3 | |||||||
| #7 | False | |||||||
| #6 | 4 | |||||||
| #7 | False | |||||||
| #9 | 2 |
Statt alle Zahlen zu durchlaufen, können wir auch von oben anfangen aufzuzählen. Diese Vorgehensweise hat den Vorteil, dass der erste gefundene gemeinsame Teiler auch der größte ist. Wir können dann die Schleife beenden, sobald wir einen gemeinsamen Teiler gefunden haben.
Da wir hierbei nicht wissen, wieviele Schleifendurchläufe gebraucht
werden, verwenden wir zur Implementierung dieser Idee eine bedingte
Schleife. Das folgende Programm bestimmt zunächst mit einer bedingten
Verzweigung die kleinere der beiden Eingabezahlen und sucht dann mit
einer bedingten Schleife abwärts nach dem größten gemeinsamen Teiler,
der schließlich mit einer print-Anweisung ausgegeben wird.
a = 4 #1
b = 6 #2
if a < b: #3
ggT = a #4
else:
ggT = b #5
while a%ggT != 0 or b%ggT != 0: #6
ggT = ggT - 1 #7
print(ggT) #8
Die folgende Tabelle dokumentiert die Ausführung dieses Programms.
| PP | a | b | a < b | ggT | a%ggT != 0 or b%ggT != 0 | Ausgabe |
|---|---|---|---|---|---|---|
| #1 | 4 | |||||
| #2 | 6 | |||||
| #3 | True | |||||
| #4 | 4 | |||||
| #6 | True | |||||
| #7 | 3 | |||||
| #6 | True | |||||
| #7 | 2 | |||||
| #6 | False | |||||
| #8 | 2 |
Setzen wir eine der Zahlen a und b gleich 0, liefert dieses
Programm einen Laufzeitfehler wegen Division durch Null. Um dies zu
verhindern müssen wir die Randfälle, in denen mindestens eine der
Eingabezahlen Null ist, prüfen und unseren Algorithmus nur dann
ausführen, wenn beide Zahlen ungleich Null sind.
a = 4
b = 6
if a == 0 and b == 0:
print("nicht definiert")
else:
if a == 0:
print(b)
if b == 0:
print(a)
if a != 0 and b != 0:
if a < b:
ggT = a
else:
ggT = b
while a%ggT != 0 or b%ggT != 0:
ggT = ggT - 1
print(ggT)
Hier zeigt sich, dass es beim Testen von Programmen wichtig ist, Randfälle systematisch zu überprüfen. Manchmal wird ein Programm leider bei korrekter Behandlung der Randfälle wie hier etwas aufgebläht.
-
Es gibt bessere Methoden zur Berechnung des ggT. Der Euklidische Algorithmus berechnet den ggT zweier Zahlen deutlich schneller als das folgende Programm. ↩︎
10.1.1 Übungsaufgaben
Aufgabe: Primzahltest
Eine Primzahl ist eine ganze Zahl größer als 1, die nur durch 1
und sich selbst teilbar ist. Schreiben Sie ein Programm, dass für eine
in der ersten Zeile zugewiesene Variable n testet, ob diese eine
Primzahl ist und das Ergebnis dieses Tests im Terminal
ausgibt. Verwenden Sie dazu die Technik Aufzählen und Testen; suchen
Sie also in einem geeigneten Zahlenbereich nach Teilern der gegebenen
Zahl.
Überlegen Sie, ob sie besser eine Zähl-Schleife oder eine bedingte Schleife verwenden und begründen Sie Ihre Wahl.
Dokumentieren Sie den Ablauf Ihres Programms tabellarisch für eine interessante Eingabe.
10.2 Teilen und Herrschen
Statt Lösungskandidaten der Reihe nach aufzuzählen, können wir einige Problem auch lösen, indem wir den durchsuchten Bereich geschickter eingrenzen. Das Verfahren Teile und Herrsche zerlegt ein Problem in, beispielsweise, zwei halb so große Teilprobleme, die dann mit der selben Technik gelöst werden können. Als Beispiel für ein solches Problem betrachten wir das Spiel Zahlenraten.
Eine Spielerin denkt sich eine Zahl zwischen 1 und 100 ohne sie zu verraten. Die Gegenspielerin muss die gedachte Zahl möglichst schnell erraten, wobei sie auf Rateversuche jedoch nur die Antworten “Ja, erraten.”, “Nein, meine Zahl ist kleiner.” oder “Nein, meine Zahl ist größer.” erhält.
Natürlich können wir, um die gedachte Zahl zu erraten einfach alle Zahlen der Reihe nach abfragen, bis wir die richtige Zahl gefunden haben. Deutlich schneller gelangen wir jedoch ans Ziel, wenn wir den durchsuchten Bereich in jedem Schritt halbieren.
Das folgende Programm implementiert diese Idee.
min = 1
max = 100
geheim = 37
erraten = False
while not erraten:
kandidat = (min + max) // 2
print("Ist die Zahl gleich " + str(kandidat) + "?")
if geheim == kandidat:
print("Ja, erraten.")
erraten = True
if geheim < kandidat:
print("Nein, meine Zahl ist kleiner!")
max = kandidat - 1
if geheim > kandidat:
print("Nein, meine Zahl ist größer!")
min = kandidat + 1
Hier wird der durchsuchte Bereich von min bis max in jedem
Schleifendurchlauf halbiert. Wenn die Zahl erraten wurde, wird die
Schleife durch die Zuweisung erraten = True beendet.
Die Ausgabe dieses Programms ist
Ist die Zahl gleich 50?
Nein, meine Zahl ist kleiner.
Ist die Zahl gleich 25?
Nein, meine Zahl ist größer.
Ist die Zahl gleich 37?
Ja, erraten.
Die gedachte Zahl wird mit dem Verfahren Teile und Herrsche in diesem
Fall also nach drei Schritten gefunden. Der Algorithmus hat in diesem
Fall Glück gehabt, weil er den Bereich garnicht bis zum Ende
eingrenzen musste. Im schlimmsten Fall nähern sich min und max bei
der Ausführung so weit an, dass sie gleich groß sind. In dem Fall ist
das Problem dann aber einfach gelöst.
10.2.1 Übungsaufgaben
Aufgabe: Programmtabelle zum Zahlenraten
Dokumentieren Sie die Ausführung des folgenden mit Programmpunkten versehenen Programms zum Zahlenraten tabellarisch. Da der Wert der Bedingungen in diesem Fall direkt aus dem Wert beteiligter Variablen hervorgeht, können Sie bei der Programmtabelle auf die Spalten für Bedingungen verzichten.
Anstelle des Programmcodes können Sie auch Ihren PAP, den Sie zu diesem Programm bereits erstellt haben, mit Programmpunkten versehen und die Programmtabelle daraus ableiten.
min = 1 #1
max = 100 #2
geheim = 37 #3
erraten = False #4
while not erraten:
kandidat = (min + max) // 2 #5
print("Ist die Zahl gleich " + str(kandidat) + "?")
#6
if geheim == kandidat:
print("Ja, erraten.") #7
erraten = True #8
if geheim < kandidat:
print("Nein, meine Zahl ist kleiner!")
#9
max = kandidat - 1 #10
if geheim > kandidat:
print("Nein, meine Zahl ist größer!")
#11
min = kandidat + 1 #12
Bonusaufgabe: Analyse zum Zahlenraten
Wieviele Fragen stellt das Programm zum Zahlenraten im ungünstigsten Fall? Geben Sie
die Ausgabe für einen solchen ungünstigsten Wert für n an.
Schreiben Sie ein Programm, dass die Technik Aufzählen und Testen verwendet um alle Zahlen n auszugeben, für die das Programm zum Zahlenraten die größtmögliche Anzahl Fragen stellt, bis die Zahl erraten wird.
Bonusaufgabe: Quadratwurzel suchen
Schreiben Sie ein Python-Programm, das Quadratwurzeln mit Hilfe der Programmiertechnik Teilen und Herrschen berechnet.
Weisen Sie die Zahl, deren Wurzel berechnet werden soll, zu Beginn des Programms einer Variablen x zu und initialisieren Sie zusätzlich eine Variable genauigkeit mit dem Wert 0.001. Letztere gibt an, mit welcher Genauigkeit die Wurzel berechnet werden soll.
Suchen Sie dann, wie beim Zahlenraten durch Intervallschachtelung, nach einem Kandidaten, der nah genug an der Wurzel von x ist, deren Quadrat nämlich nicht mehr als genauigkeit von x abweicht. Passen Sie also die Grenzen des durchsuchten Intervalls so lange geeignet an, bis die gewünschte Genauigkeit erreicht ist, und geben Sie dann den Kandidaten für die Quadratwurzel aus.
Hinweis: Um Wurzeln beliebiger positiver Zahlen berechnen zu können, sollten sie mit Fließkommazahlen rechnen, um die Verwendung ganzzahliger Division zu vermeiden.
Zusatzaufgabe: Wandeln Sie Ihr Programm so ab, dass zusätzlich zur berechneten Näherung für die Wurzel auch die Anzahl der benötigten Schleifendurchläufe ausgegeben wird.
10.3 Vertiefung
Dieser Abschnitt beschreibt Programme, die die bisher behandelten Sprachmittel imperativer Programmiersprachen am Beispiel neuer Algorithmen vertiefen.
Geschachtelte Wiederholungen
Bisher kamen in den Wiederholungsrümpfen unserer Programme keine weiteren Wiederholungen vor. Insbesondere beim Aufzählen und Überprüfen kann es passieren, dass Wiederholungen geschachtelt werden, wenn der Test selbst eine Wiederholung verwendet oder mehrere Wiederholungen verwendet werden, um Kandidaten aufzuzählen.
Als Beispiel für ein Programm, das Kandidaten mit Hilfe mehrerer geschachtelter Wiederholungen aufzählt, berechnen wir sogenannte Pythagoräische Tripel. Positive ganze Zahlen \(a \leq b \leq c\) heißen Pythagoräisches Tripel, wenn \(a^2 + b^2 = c^2\) gilt. Das folgende Programm listet alle solche Tripel aus Werten zwischen 1 und 20 auf.
n = 20
for a in range(1, n+1):
for b in range(a, n+1):
for c in range(b, n+1):
if a*a + b*b == c*c:
print(str(a) + ', ' + str(b) + ', ' + str(c))
Hier besteht der Test aus einer einfachen Bedingung, aber die Aufzählung geschieht mit Hilfe von drei geschachtelten Wiederholungen mit fester Anzahl.
Die Ausgabe dieses Programms ist
3, 4, 5
5, 12, 13
6, 8, 10
8, 15, 17
9, 12, 15
12, 16, 20
Als Beispiel für die Programmiertechnik Aufzählen und Überprüfen, bei dem auch der Test eine Wiederholung verwendet, berechnen wir vollkommene Zahlen. Eine Zahl heißt vollkommen, wenn sie gleich der Summe aller ihrer Teiler ist, die kleiner sind als sie selbst. Die kleinste vollkommene Zahl ist 6, deren Teiler 1, 2 und 3 sind, die addiert wieder 6 ergeben. Dasselbe gilt für 28 = 1+2+4+7+14.
Das folgende Programm gibt alle vollkommenen Zahlen zwischen 1 und 1000 aus:
n = 1000
for i in range(1, n+1):
sum = 0
for j in range(1, i):
if i%j == 0:
sum = sum + j
if i == sum:
print(i)
Hier besteht der Test aus der Berechnung der Summe aller kleineren Teiler von i und dem anschließenden Vergleich dieser Summe mit i.
Die Ausgabe dieses Programms ist
6
28
496
Anscheinend gibt es relativ wenige vollkommene Zahlen.
Euklidischer Algorithmus
Der größte gemeinsame Teiler zweier Zahlen lässt sich mit dem Euklidischen Algorithmus berechnen. Der Algorithmus wurde etwa 300 v. Chr. von Euklid beschrieben und ist einer der ältesten heute noch verwendeten Algorithmen. Der Algorithmus basiert auf der Idee, dass der größte gemeinsame Teiler zweier natürlicher Zahlen sich nicht ändert, wenn man die größere Zahl durch die Differenz der beiden Zahlen ersetzt. Es genügt also, den ggT dieser beiden neuen Zahlen zu berechnen, wodurch das Problem verkleinert wird.1 Dieses Verfahren wird so lange fortgesetzt, bis beide Zahlen gleich groß sind. Sie entsprechen dann dem ggT der ursprünglichen Zahlen.
Als Beispiel berechnen wir den ggT der Zahlen 49 und 21 anhand dieser Idee:
- \(ggT(49,21) = ggT(49-21,21) = ggT(28,21)\)
- \(ggT(28,21) = ggT(28-21,21) = ggT(7,21)\)
- \(ggT(7,21) = ggT(7,21-7) = ggT(7,14)\)
- \(ggT(7,14) = ggT(7,14-7) = ggT(7,7)\)
- \(ggT(7,7) = 7\)
Also ist der ggT von 49 und 21 gleich 7.
Wir implementieren nun die Anwendung des Euklidischen Algorithmus auf 49 und 21 in Python. Zu Beginn des Programms weisen wir die Eingabezahlen zwei Variablen a und b zu. Anschließend weisen wir schrittweise der größeren der beiden Variablen die Differenz der gespeicherten Zahlen zu, bis beide Variablen, die gleiche Zahl enthalten. Da wir nicht wissen, wieviele Schritte dazu notwendig sind, verwenden wir eine bedingte Wiederholung.
a = 49 #1
b = 21 #2
while a != b: #3
if a > b: #4
a = a - b #5
else:
b = b - a #6
print(a) #7
Zur Veranschaulichung werten wir dieses Programm wie folgt tabellarisch aus.
| PP | a |
b |
a != b |
a > b |
Ausgabe |
|---|---|---|---|---|---|
| #1 | 49 | ||||
| #2 | 21 | ||||
| #3 | True |
||||
| #4 | True |
||||
| #5 | 28 | ||||
| #3 | True |
||||
| #4 | True |
||||
| #5 | 7 | ||||
| #3 | True |
||||
| #4 | False |
||||
| #6 | 14 | ||||
| 3# | True |
||||
| #4 | False |
||||
| #6 | 7 | ||||
| #3 | False |
||||
| #7 | 7 |
In diesem Beispiel wird deutlich, dass unter Umständen eine Variable mehrfach von der anderen abgezogen wird; nämlich solange wie das Ergebnis größer ist als die abgezogene Zahl. Im obigen Beispiel wird die 21 zunächst von 49 und dann von 28 abgezogen, bis das Ergebnis 7 ist. Dann wird die 7 zuerst von 21 und dann von 14 abgezogen, bis das Ergebnis 7 ist. Der beschriebene Prozess der wiederholten Subtraktion der 21 von 49 endet mit dem Rest der Division von 49 durch 21. Würden wir die 7 am Ende noch einmal von 7 abziehen, würde der Prozess der wiederholten Subtraktion der 7 von 21 ebenfalls mit dem Rest der Division von 21 durch 7 enden. Diese Idee können wir verwenden, um die Anzahl der Wiederholungs-Durchläufe bei der Berechnung des Euklidischen Algorithmus zu verringern, indem wir die Subtraktion durch den Modulo-Operator ersetzen.
a = 49 #1
b = 21 #2
while a >= 0 and b != 0: #3
if a > b: #4
a = a % b #5
else:
b = b % a #6
print(a+b) #7
Als Wiederholungsbedingung testen wir, dass keine der Eingabezahlen Null ist, um Division durch Null zu vermeiden. Die Bedingung a != b kann entfallen, da in dem Fall im nächsten wiederholungsdurchlauf a = 0 gesetzt wird, wonach die Wiederholung endet und die Ausgabe-Anweisung a+b, also b ausgibt. Da am Ende der Wiederholung entweder a oder b gleich Null ist und die andere Variable das Ergebnis enthält, können wir die beiden Variablen einfach aufsummieren, um das Ergebnis auszugeben.
Die folgende Tabelle dokumentiert die Ausführung dieses Programms:
| PP | a |
b |
a != 0 and b != 0 |
a < b |
Ausgabe |
|---|---|---|---|---|---|
| #1 | 49 | ||||
| #2 | 21 | ||||
| #3 | True |
||||
| #4 | False |
||||
| #6 | 7 | ||||
| #3 | Truè |
||||
| #4 | True |
||||
| #5 | 0 | ||||
| #3 | False |
||||
| #7 | 7 |
Diese Implementierung verwendet nur noch halb so viele Wiederholungsdurchläufe wie die vorherige. Außerdem wechselt der Test der Bedingung a < b in jedem Durchlauf seinen Wert.
Da der Divisionsrest immer kleiner ist als die Zahl, durch die geteilt wurde, ist der Vergleich innerhalb des Wiederholungs-Rumpfes, welche der beiden Variablen a und b größer ist, nicht mehr nötig. Stattdessen können wir die Rollen der Variablen in jedem Schritt vertauschen und den Algorithmus beenden, sobald der berechnete Divisionsrest Null ist. Das folgende Programm implementiert diese Idee.
a = 49 #1
b = 21 #2
while b != 0: #3
x = b #4
b = a % b #5
a = x #6
print(a+b) #7
Dieses Programm kommt ebenfalls mit der Hälfte der Wiederholungsdurchläufe aus, wie die tabellarische Auswertung zeigt. Statt drei Vergleichen benötigen wir pro Durchlauf nur noch einen:
| PP | a |
b |
b != 0 |
x |
Ausgabe |
|---|---|---|---|---|---|
| #1 | 49 | ||||
| #2 | 21 | ||||
| #3 | True |
||||
| #4 | 21 | ||||
| #5 | 7 | ||||
| #6 | 21 | ||||
| #3 | True |
||||
| #4 | 7 | ||||
| #5 | 0 | ||||
| #6 | 7 | ||||
| #3 | False |
||||
| #7 | 7 |
Im Allgemeinen lässt sich zeigen, dass diese Variante des Euklidischen Algorithmus höchstens fünfmal so viele Schritte benötigt, wie die Anzahl der Ziffern der kleineren Zahl. Der Beweis dieser Eigenschaft markierte 1844 den Beginn der Komplexitätstheorie, die heute als Teil der Theoretischen Informatik erforscht wird.
-
Da das Problem wie beschrieben auf ein kleineres Problem zurückgeführt wird, fassen einige den Euklidischen Algorithmus unter die Technik “Teile und herrsche”. Da das Ausgangsproblem allerdings nur auf ein einziges kleineres Problem zurückgeführt wird, ist es fraglich, ob hier von “Teilen” die Rede sein kann. ↩︎
10.3.1 Übungsaufgaben
Bonusaufgabe: Primzahlen aufzählen
Schreiben Sie ein Programm, dass alle Primzahlen bis zu einer in der ersten Programmzeile zugewiesenen Obergrenze ausgibt. Diskutieren Sie, inwiefern Ihre Lösung der Programmiertechnik “Aufzählen und Überprüfen” folgt.
10.4 Quellen und Lesetipps
10.5 Lösungen
Aufgabe: Primzahltest
Hier ist ein Programm, dass testet, ob der Wert der Variable n eine Primzahl ist.
Wir gehen dabei davon aus, dass dieser Wert eine natürliche Zahl ist.
n = 21 #1
teilbar = False #2
k = 2 #3
while not teilbar and k*k <= n: #4
teilbar = (n % k) == 0 #5
k = k + 1 #6
print(n > 1 and not teilbar) #7
Wir suchen mit einer bedingten Schleife nach dem kleinsten Teiler von n,
der größer als eins und ungleich n ist.
Dabei können wir abbrechen,
wenn wir alle Zahlen probiert haben, deren Quadrat kleiner oder gleich n ist,
da der gesuchte Teiler nicht größer sein kann.
Für die Ausgabe testen wir zusätzlich, ob n größer als eins ist,
da die eins keine Primzahl ist, obwohl sie keinen Teiler größer als eins hat.
Wir verwenden eine bedingte Schleife, um bei gefundenem Teiler abzubrechen. Es ist also unklar, wie oft der Schleifenrumpf ausgeführt wird.
Die folgende Tabelle dokumentiert die Ausführung des obigen Programms.
| PP | n | teilbar | k | !teilbar && k*k<=n | Ausgabe |
|---|---|---|---|---|---|
| #1 | 21 | ||||
| #2 | False | ||||
| #3 | 2 | ||||
| #4 | True | ||||
| #5 | False | ||||
| #6 | 3 | ||||
| #4 | True | ||||
| #5 | True | ||||
| #6 | 4 | ||||
| #4 | False | ||||
| #7 | False |
Aufgabe: Programmtabelle zum Zahlenraten
| PP | min | max | geheim | erraten | kandidat | Ausgabe |
|---|---|---|---|---|---|---|
| #1 | 1 | |||||
| #2 | 100 | |||||
| #3 | 37 | |||||
| #4 | False | |||||
| #5 | 50 | |||||
| #6 | Ist die Zahl gleich 50? | |||||
| #9 | Nein, meine Zahl ist kleiner! | |||||
| #10 | 49 | |||||
| #5 | 25 | |||||
| #6 | Ist die Zahl gleich 25? | |||||
| #11 | Nein, meine Zahl ist größer! | |||||
| #12 | 26 | |||||
| #5 | 37 | |||||
| #6 | Ist die Zahl gleich 37? | |||||
| #7 | Ja, erraten. |
Bonusaufgabe: Analyse zum Zahlenraten
Die maximale Anzahl Fragen, die das Programm stellt, ist sieben (siehe unten).
Diese Zahl wird zum Beispiel bei n = 2 erreicht, wie die folgende Ausgabe demonstriert.
Ist die Zahl gleich 50?
Nein, meine Zahl ist kleiner!
Ist die Zahl gleich 25?
Nein, meine Zahl ist kleiner!
Ist die Zahl gleich 12?
Nein, meine Zahl ist kleiner!
Ist die Zahl gleich 6?
Nein, meine Zahl ist kleiner!
Ist die Zahl gleich 3?
Nein, meine Zahl ist kleiner!
Ist die Zahl gleich 1?
Nein, meine Zahl ist größer!
Ist die Zahl gleich 2?
Ja, erraten.
Um die maximale Anzahl von Fragen systematisch zu bestimmen, passen wir das Programm so an, dass für alle Zahlen zwischen 1 und 100 die gestellten Fragen gezählt werden.
maxcount = 0
for geheim in range(1,101):
min = 1
max = 100
erraten = False
count = 0
while not erraten:
kandidat = (min + max) // 2
count = count + 1
if geheim == kandidat:
erraten = True
if geheim < kandidat:
max = kandidat - 1
if geheim > kandidat:
min = kandidat + 1
if count > maxcount:
maxcount = count
print(maxcount)
Dieses Programm gibt tatsächlich 7 aus. Wir passen das Programm nun so an, dass es alle Zahlen, für die sieben Fragen gestellt werden, ausgibt.
maxcount = 0
for geheim in range(1,101):
min = 1
max = 100
erraten = False
count = 0
while not erraten:
kandidat = (min + max) // 2
count = count + 1
if geheim == kandidat:
erraten = True
if geheim < kandidat:
max = kandidat - 1
if geheim > kandidat:
min = kandidat + 1
if count > maxcount:
maxcount = count
if count == 7:
print(geheim)
Es gibt eine ganze Reihe von Zahlen, für die das Programm sieben Fragen braucht, deshalb verzichten wir an dieser Stelle darauf, die Ausgabe des Programms aufzulisten.
Bonusaufgabe: Quadratwurzel suchen
x = 100.0
genauigkeit = 0.001
min = 0.0
max = x
nah_genug = False
count = 0
while not nah_genug:
kandidat = (min + max) / 2
fehler = x - kandidat**2
if -genauigkeit < fehler and fehler < genauigkeit:
nah_genug = True
if fehler < 0:
max = kandidat
else:
min = kandidat
count = count + 1
print(kandidat)
print(count)
Bonusaufgabe: Primzahlen aufzählen
Zum Aufzählen aller Primzahlen schachteln wir die Lösung aus einer vorherigen Aufgabe in eine Zählschleife ein, die alle Zahlen bis zur gegebenen Obergrenze durchläuft. Diejenigen Zahlen, die den Primzahltest bestehen, werden dann im Rumpf der Zählschleife ausgegeben.
max = 1000
for n in range(2,max+1):
teilbar = False
k = 2
while not teilbar and k*k <= n:
teilbar = (n % k) == 0
k = k + 1
if not teilbar:
print(n)
Den Test n > 1 aus der vorherigen Aufgabe brauchen wir hier am Ende nicht zu verwenden, da die Zählvariable n nur Werte größer gleich zwei durchläuft.
Diese Implementierung zählt alle Zahlen bis zur Obergrenze auf und überprüft die Primzahleigenschaft für jede aufgezählte Zahl. Der Primzahltest verwendet seinerseits die Technik Aufzählen und Überprüfen, um Kandidaten für Teiler aufzuzählen und dann auf die Teilbarkeits-Eigenschaft zu überprüfen. Es handelt sich also um eine geschachtelte Anwendung der diskutierten Programmiertechnik.
11. Funktionen und Prozeduren
11.1 Abstraktion von Ausdrücken durch Funktionen
Maximum zweier Zahlen
Einen Ausdruck zur Berechnung des Maximums zweier Zahlen können wir zum Beispiel wie folgt als Funktion abstrahieren:
def max(x, y):
if x > y:
z = x
else:
z = y
return z
Das Schlüsselwort def leitet die Funktionsdefinition ein, max ist der Name der definierten Funktion und die Variablen x und y heißen formale Parameter der Funktion max. Der sogenannte Funktionsrumpf enthält die bedingte Anweisung zur Berechnung des Maximums z der Werte von x und y. In der letzten Zeile wird mit Hilfe des Schlüsselwortes return der Wert von z als Rückgabewert der Funktion max festgelegt.
Eine Rückgabe-Anweisung mittels return beendet die Ausführung des Funktionsrumpfes auch dann, wenn sie nicht an dessen Ende steht. Wir können deshalb die Funktion max auch etwas kürzer wie folgt definieren:
def max(x, y):
if x > y:
return x
else:
return y
Wenn wir diese Funktion in einem Python-Programm maxFun.py speichern, können wir es wie folgt in die interaktive Python-Shell einbinden und ausführen:
>>> from maxFun import *
>>> max(2,3)
3
>>>
Die import-Anweisung bewirkt also, dass max() als eine vordefinierte Funktion verwendet werden kann.
Um das Maximum dreier Zahlen zu berechnen, können wir nun statt einer geschachtelten bedingten Anweisung geschachtelte Funktions-Aufrufe verwenden:
>>> from maxFun import *
>>> max(1,max(3,2))
3
>>>
Bei der Auswertung eines Funktionsaufrufes werden zunächst die Argumente (auch aktuelle Parameter genannt) ausgewertet und dann in den Funktionsrumpf eingesetzt. Wir können die Auswertungsreihenfolge sichtbar machen, indem wir Ausgaben in den Funktionsrumpf einbauen:
def max(x, y):
print('Aufruf: max(' + str(x) + ', ' + str(y) + ')')
if x > y:
print('Rückgabewert: ' + str(x))
return x
else:
print('Rückgabewert: ' + str(y))
return y
Nachdem wir das Programm mit der import-Anweisung neu geladen haben, können wir den obigen Ausdruck mit den eingefügten Ausgaben auswerten:
>>> from maxFun import *
>>> max(1, max(2, 3))
Aufruf: max(2, 3)
Rückgabewert: 3
Aufruf: max(1, 3)
Rückgabewert: 3
3
Hierbei erkennen wir, dass zunächst der Aufruf max(2, 3) zu 3 ausgewertet wird. Danach wird dieses Ergebnis als Argument des äußeren Aufrufs von max verwendet. Der Aufruf max(1, 3) wird dann zu 3 ausgewertet.
Ausgaben wie hier sind oft nützlich zur Fehlersuche in Programmen. Zugunsten einer Trennung von Ausdrücken und Anweisungen sollte aber in Funktionen in der Regel auf Ausgaben verzichtet werden.
Beachten Sie den Unterschied zwischen Ausgabe-Anweisungen zur Ausgabe eines Wertes im Terminal und Rückgabe-Anweisungen zur Festlegung des Rückgabewertes von Funktionen. Eine Ausgabe-Anweisung legt keinen Rückgabewert fest und eine Rückgabe-Anweisung erzeugt keine Ausgabe im Terminal!
Primzahltest
Als weiteres Beispiel für Abstraktion durch Funktionen betrachten wir die Aufzählung aller Primzahlen bis zu einer gegebenen Obergrenze. Wenn wir den Primzahltest als Funktion is_prime(n) abstrahieren, können wir ihn in einer Wiederholung mit fester Anzahl aufrufen, statt die Definition des Tests in die Wiederholung zu kopieren.
def is_prime(n):
teilbar = False
k = 2
while not teilbar and k*k <= n:
teilbar = (n % k) == 0
k = k + 1
return(n > 1 and not teilbar)
max = 100
for i in range(2,max+1):
if is_prime(i):
print(i)
Die Funktion is_prime() liefert einen Wahrheitswert zurück und wird deshalb auch Prädikat genannt. Es ist eine Konvention, die Namen von Prädikaten wie Fragen zu formulieren. Prädikate in Python werden oft mit dem Präfix is_ benannt. Dies ist nicht vorgeschrieben, erhöht aber die Lesbarkeit.
Das definierte Prädikat is_prime() wird in einer Zählschleife nach seiner Definition aufgerufen. Sein Ergebnis wird mit einer bedingten Anweisung überprüft um alle Primzahlen zwischen 2 und max auszugeben.
Funktionen müssen in Python vor ihrem ersten Aufruf definiert werden.
11.1.1 Übungsaufgaben
Aufgabe: Funktionen definieren
Definieren Sie die folgenden Funktionen:
max3mit drei Parameternx,yundzzur Berechnung des Maximums der drei Parameter.nicht,undundoderfür logische Negation, Konjunktion und Disjunktion von Wahrheitswerten ohne Verwendung vordefinierter logischer Operatoren.sumUpTomit einem Parameternzur Berechnung der Summe der Zahlen von1bisn.factorialmit einem Parameternzur Berechnung der Fakultät vonn.
Testen Sie Ihre Definitionen in der interaktiven python-Shell und geben Sie einige Beispielaufrufe an.
Bonusaufgabe: Heron-Verfahren programmieren
Definieren Sie eine Funktion heronIter mit zwei Parametern x und eps zur Wurzel-Iteration nach dem Heron-Verfahren. Der Rückgabewert der Funktion soll die Wurzel aus x mit der Genauigkeit eps sein.
Aufgabe: Summe von Zahlenbereichen
Definieren Sie eine Funktion sum_from_to mit zwei Parametern n und m, die als Ergebnis die Summe aller Zahlen von n bis m zurückgibt. Zum Beispiel soll das Ergebnis des Aufrufs sum_from_to(4,7) gleich 22 sein, weil 4+5+6+7 = 22 ist.
Setzten Sie voraus, dass n und m ganze Zahlen sind für die n <= m gilt. Sie brauchen diese Bedingung in Ihrer Implementierung also nicht zu testen.
Implementieren Sie die Funktion einmal mit einer Zählschleife und einmal mit einer bedingten Schleife. Welche Variante bevorzugen Sie und warum?
Bonusaufgabe: Binärdarstellung positiver Zahlen
Schreiben Sie unter Verwendung einer geeigneten Schleife eine Funktion binary mit einem Parameter n, die eine positive ganze Zahl als Argument erwartet und deren Binärdarstellung als Zeichnekette zurück gibt. Hier sind einige Beispielaufrufe, die das Verhalten der Funktion verdeutlichen:
>>> binary(1)
'1'
>>> binary(2)
'10'
>>> binary(3)
'11'
>>> binary(4)
'100'
>>> binary(42)
'101010'
11.2 Benutzereingaben verarbeiten
Bisher haben wir Beispiel-Eingaben immer direkt im Quelltext codiert oder als Parameter von Funktionen oder Prozeduren in der Python-Shell eingegeben. Im Folgenden diskutieren wir, wie wir Benutzereingaben im Terminal verarbeiten können.
Python stellt eine vordefinierte Funktion input() zur Verfügung, mit deren Hilfe eine Zeile im Terminal eingelesen werden kann. Bei einem Aufruf von input() wird die Abarbeitung des Programms so lange angehalten, bis eine Zeile (abgeschlossen mit der Enter-Taste) im Terminal eingegeben wurde. Das Ergebnis von input() ist die eingegebene Zeichenkette.
input() akzeptiert eine Eingabeaufforderung als Parameter.
Die folgenden Aufrufe in der Python-Shell zeigen von input() gelieferte Ergebnisse.
>>> input()
Hallo # Eingabe des Benutzers
'Hallo' # Rückgabe des input-Aufrufs
>>> input('Wer schrieb das erste Computerprogramm? - ')
Wer schrieb das erste Computerprogramm? - Ada Lovelace
'Ada Lovelace'
Nach dem Aufruf von input() wartet die Python-Shell auf eine Benutzereingabe. Nachdem wir etwas eingegeben und die Enter-Taste gedrückt haben, wird das Ergebnis als Zeichenkette zurückgegeben.
Interaktiv das Maximum zweier Zahlen berechnen
Wir können input() wie folgt verwenden, um die Eingaben für
die von uns definierte Funktion max im Terminal einzulesen.
a = int(input('Gib eine ganze Zahl ein: '))
b = int(input('Gib noch eine ganze Zahl ein: '))
print('Die größere von beiden ist ' + str(max(a, b)) + '.')
Wenn wir dieses Programm ausführen, werden wir zunächst nach zwei Zahlen gefragt und dann wird die größere von beiden ausgegeben:
Gib eine ganze Zahl ein: 5
Gib noch eine ganze Zahl ein: 42
Die größere von beiden ist 42.
input() gibt immer eine Zeichenkette als Ergebnis zurück. Deswegen müssen wir die Eingaben mit int() in ganze Zahlen umwandeln. Die eingelesenen Zahlen reichen wir als Argumente an die Funktion max() weiter, deren Ergebnis wir mit str() wieder in eine Zeichenkette umwandeln, um es ausgeben zu können.
Interaktiver Primzahltest
Wir können Benutzereingaben auch in einer Schleife einlesen, um interaktive Programme zu schreiben, die mit ihren Benutzern kommunizieren. Das folgende Programm fragt zum Beispiel so lange nach Eingaben, wie positive Zahlen eingegeben werden (dies wird mit isnumeric() geprüft), und gibt dann aus, ob es sich bei der eingegebenen Zahl um eine Primzahl handelt.
s = input('Gib eine Zahl ein: ')
while s.isnumeric() and int(s) > 0:
n = int(s)
if is_prime(n):
print(str(n) + ' ist eine Primzahl.')
else:
print(str(n) + ' ist keine Primzahl.')
s = input('Gib noch eine Zahl ein: ')
Hier ist eine Beispiel-Interaktion mit diesem Programm:
Gib eine Zahl ein: 17
17 ist eine Primzahl.
Gib noch eine Zahl ein: 21
21 ist keine Primzahl.
Gib noch eine Zahl ein: quit
Nach Eingabe von quit wird die Schleife beendet, und es werden keine weiteren Fragen mehr gestellt.
Zahlenraten mit Benutzereingabe
Wir können nun auch unser Programm zum Zahlenraten so abwandeln, dass es eine vom Benutzer gedachte Zahl errät.
min = 1
max = 100
erraten = False
while not erraten:
if min == max:
print("Die Zahl ist " + str(min) + ".")
erraten = True
else:
kandidat = (min + max) // 2
antwort = input("Ist die Zahl " + str(kandidat) + "? ")
if antwort == "=":
erraten = True
if antwort == "<":
max = kandidat - 1
if antwort == ">":
min = kandidat + 1
Hier ist eine Beispiel-Interaktion mit diesem Programm:
Ist die Zahl 50? <
Ist die Zahl 25? >
Ist die Zahl 37? >
Ist die Zahl 43? <
Ist die Zahl 40? >
Ist die Zahl 41? >
Die Zahl ist 42.
11.2.1 Übungsaufgaben
Aufgabe: Eingaben verarbeiten
Schreiben Sie Python-Programm, das nacheinander zwei ganze Zahlen im Terminal einliest und dann eine Ausgabe erzeugt, die die eingegebenen Zahlen bezüglich ihrer Größe vergleicht. Wie verhält sich ihr Programm bei einer ungültigen Eingabe?
Erweitern Sie Ihr Programm gegebenenfalls so, dass solange nach Eingaben gefragt wird, bis diese gültig sind, bevor die Ausgabe erzeugt wird.
Bonusaufgabe: Stein, Schere, Papier
Schreiben Sie ein Python-Programm, das mit dem Benutzer das Spiel “Stein, Schere, Papier” spielt und dabei immer gewinnt. Das Programm soll die Wahl des Benutzers im Terminal einlesen und dann blitzschnell seine Wahl so treffen, dass der Benutzer verliert. Das Spiel soll so lange wiederholt werden, wie der Benutzer gültige Eingaben tätigt.
Eine Beispielinteraktion mit dem Programm könnte zum Beispiel so aussehen.
Stein, Schere oder Papier?
Papier
Ich hatte Schere genommen. Gewonnen!
Stein, Schere oder Papier?
Schere
Ich hatte Stein genommen. Gewonnen!
Stein, Schere oder Papier?
Aufgabe: Gängige Fehler
In dieser Aufgabe sollen sie üben, Fehler in Python-Programmen zu finden. Dokumentieren Sie für jedes der folgenden Programme die Fehlermeldung bzw. dokumentieren Sie einen Testfall, der zeigt, dass sich das Programm nicht wie (vermutlich) beabsichtigt verhält. Erklären Sie jeweils den Fehler im Programm und korrigieren Sie es.
a)
def is_small_prime(n):
if n == 2 or 3 or 5 or 7:
return True
else
return False
b)
def describe_text(s):
if len(s) >= 10:
print("10 Zeichen oder mehr")
if len(s) > 20:
print("Auch mehr als 20")
else:
print("Weniger als 10 Zeichen")
Aufgabe: Zahlenbereiche als Zeichenkette
Schreiben Sie eine Funktion nums_from_to() mit zwei Parametern lower und upper, die eine Zeichenkette der Zahlen im übergebenen Bereich zurückliefert. Die Zahlen sollen dabei durch Leerzeichen getrennt werden. Zum Beispiel soll der Aufruf nums_from_to(4,7) zur Zeichenkette "4 5 6 7" ausgewertet werden.
Schreiben Sie eine Prozedur, die nacheinander zwei Zahlen vom Benutzer einliest und alle Zahlen im gegebenen Bereich hintereinander ausgibt. Was wird ausgegeben, wenn die zweite Zahl nicht größer ist als die erste und warum?
11.3 Abstraktion von Anweisungen durch Prozeduren
Das Programm zur Ausgabe aller Primzahlen bis zu einer Obergrenze legt die Obergrenze im Programmtext fest. Statt alle Primzahlen bis zu einer konkreten Obergrenze auszugeben, können wir auch ein Programm zur Ausgabe aller Primzahlen bis zu einer beliebigen Obergrenze schreiben. Dazu abstrahieren wir die Zählschleife mit Hilfe einer Prozedur primes_up_to
mit einem Parameter max.
def primes_up_to(max):
for i in range(2, max+1):
if is_prime(i):
print(i)
Nun können wir z.B. in der interaktiven Python-Shell die Anweisungen primes_up_to(100) und primes_up_to(1000) ausführen, um alle Primzahlen bis 100 bzw. 1000 im Terminal auszugeben.
Prozeduren haben keinen Rückgabewert, enthalten also keine return-Anweisung. Sie können verwendet werden, um mit print-Anweisungen komplexe Ausgaben im Terminal zu erzeugen.
Zum Beispiel gibt die folgende Prozedur den Umriss eines Quadrats aus Sternchen im Terminal aus:
def put_quadrat(size):
line = ''
for i in range(0,size):
line = line + '*'
inside = ''
for i in range(0, size-2):
inside = inside + ' '
print(line)
for i in range(0, size-2):
print('*' + inside + '*')
print(line)
Da wir das Quadrat zeilenweise ausgeben müssen, berechnen wir zunächst den oberen Rand als Zeile aus Sternchen
gegebener Länge und speichern ihn in der Variable line. Danach berechnen wir das Innere als um zwei Zeichen kürzere
Zeile inside aus Leerzeichen. Im Anschluss geben wir den
oberen Rand gefolgt von Zeilen, die das Innere mit Sternchen
umranden aus. Schließlich geben wir noch einmal line als
unteren Rand aus.
Hier sind zwei Beispielausgaben dieser Prozedur in der Python-Shell:
>>> from quadrat import *
>>> put_quadrat(3)
***
* *
***
>>> put_quadrat(5)
*****
* *
* *
* *
*****
Bei der Definition der Prozedur put_quadrat fällt eine Ähnlichkeit des Codes zur Berechnung der oberen und unteren Zeile sowie des inneren des Quadrates auf. Beide Male wird eine gegebene Zeichenkette eine bestimmte Anzahl oft wiederholt. Wir können unser Programm vereinfachen, indem wir diese Berechnung als Funktion abstrahieren und dann innerhalb von
put_quadrat verwenden:
def repeat(times, string):
result = ''
for i in range(0, times):
result = result + string
return result
def put_quadrat(size):
print(repeat(size, '*'))
for i in range(0, size-2):
print('*' + repeat(size-2, ' ') + '*')
print(repeat(size, '*'))
Der Rückgabewert der Funktion repeat ist eine Zeichenkette. Innerhalb der Prozedur put_quadrat werden verschiedene
solcher Zeichenketten berechnet und mit print-Anweisungen im Terminal ausgegeben.
11.3.1 Übungsaufgaben
Hausaufgabe: Prozeduren definieren
Definieren Sie eine Prozedur putDreieck() mit einem Parameter size
zur Ausgabe eines rechtwinklingen Dreiecks gegebener Kantenlänge. Für
den Parameter 4 soll die folgende Ausgabe erzeugt werden.
*
**
* *
****
Suchen Sie nach sich wiederholenden Mustern in Ihrer Implementierung und definieren Sie gegebenenfalls geeignete Funktionen oder Prozeduren um Ihre Implementierung zu vereinfachen.
Bonusaufgabe: Collatz-Folge visualisieren
Definieren Sie eine Prozedur putHailstone() mit einem Parameter n,
die nacheinander Zeilen aus Sternen nach dem folgenden Schema
ausgibt:
-
Solange
ngrößer als1ist, gib eine Zeile ausnSternen aus und weiseneinen neuen Wert zu. Wennngerade ist, halbiere es. Wenn nicht, setze den Wert auf3*n + 1. -
Ist
ngleich1, gib einen Stern aus.
Für den Parameter 6 soll die Prozedur die folgende Ausgabe erzeugen.
******
***
**********
*****
****************
********
****
**
*
Bonusaufgabe: Geschachtelte bedingte Anweisungen
Schreiben Sie eine Prozedur, die die Zahlen von 1 bis zu einer übergegebenen Zahl ausgibt und zu jeder Zahl jeweils noch folgenden Hinweis hinzufügt:
-
Vielfache von
2sollen durch “geht durch 2” ergänzt werden. -
Vielfache von
3sollen durch “geht durch 3” ergänzt werden. -
Zahlen, die Vielfache sowohl von
2als auch von3sind, sollen durch “geht durch 2 und 3” ergänzt werden. -
alle anderen Zahlen sollen durch “
geht weder durch 2 noch 3” ergänzt werden.
Für das Argument 10 soll die Ausgabe der Prozedur also so aussehen:
1 geht weder durch 2 noch 3
2 geht durch 2
3 geht durch 3
4 geht durch 2
5 geht weder durch 2 noch 3
6 geht durch 2 und 3
7 geht weder durch 2 noch 3
8 geht durch 2
9 geht durch 3
10 geht durch 2
Aufgabe: Funktionen und Prozeduren beschreiben
Betrachten Sie das folgende python-Programm.
def is_divisible(n,k):
return (n%k == 0)
def is_prime(n):
k = 2
while k*k <= n:
if is_divisible(n,k):
return False
k = k + 1
return (n > 1)
def print_prime_twins(to):
for n in range(1,to+1):
if is_prime(n) and is_prime(n+2):
print(str(n) + "," + str(n+2))
print_prime_twins(100)
-
Erläutern Sie das gezeigte Programm, dessen Arbeitsweise sowie dessen Ausgabe unter Verwendung der Begriffe Programm, Funktion, Prozedur, Argument, Parameter, Rückgabewert, Rumpf, Aufruf, Wahrheitswert, Variable, Anweisung, Zuweisung, Ausdruck, Wert und Schleife. Benennen Sie dabei komplexe Anweisungen mit ihrer korrekten Bezeichnung.
-
Unterziehen Sie den verwendeten Programmierstil einer kritischen Betrachtung mit Blick auf Verständlichkeit für Personen, die das Programm lesen.
11.4 Lösungen
Lösungen
Aufgabe: Funktionen definieren
Die Maximumsfunktion mit drei Parametern können wir auf die mit zwei zurückführen.
def max(x,y):
if x > y:
return x
else:
return y
def max3(x,y,z):
return max(x,max(y,z))
Beispielaufrufe:
>>> max3(1,2,3)
3
>>> max3(3,1,2)
3
>>> max3(3,4,3)
4
Bei der Implementierung der logischen Funktionen führen wir die Disjunktion mit Hilfe der Gesetze von de Morgan auf die beiden anderen Definitionen zurück.
def nicht(x):
if x:
return False
else:
return True
def und(x,y):
if x:
return y
else:
return False
def oder(x,y):
return nicht(und(nicht(x),nicht(y)))
Die Summe der ersten n Zahlen berechnen wir mit einer Zählschleife.
def sum_up_to(n):
sum = 0
for i in range(n+1):
sum = sum + i
return sum
Beispielaufruf:
>>> sum_up_to(100)
5050
Analog dazu berechnen wir die Fakultät als Produkt der ersten n
Zahlen und initialisieren dazu die Variable prod mit dem neutralen
Element 1 der Multiplikation.
def factorial(n):
prod = 1
for i in range(1,n+1):
prod = prod * i
return prod
Beispielaufrufe:
>>> factorial(3)
6
>>> factorial(10)
3628800
Zur Wurzelberechnung mit dem Heron-Verfahren verbessern wir eine initial gewählte Näherung solange, bis sie nah genug an der Wurzel ist. Um die Lesbarkeit zu erhöhen, führen wir zwei Hilfsfunktionen ein. Eine zum Testen, ob die Nährerung gut genug ist und eine um eine Näherung zu verbessern.
def is_close_enough(x,sqrt,eps):
diff = sqrt**2 - x
return -eps < diff and diff < eps
def improve(x,sqrt):
return (sqrt + x/sqrt)/2
Mit Hilfe dieser Funktionen können wir die Wurzeliteration nun mit einer einfachen bedingten Schleife programmieren.
def heronIter(x,eps):
sqrt = 1.0
while not is_close_enough(x,sqrt,eps):
sqrt = improve(x,sqrt)
return sqrt
Beispielaufrufe:
>>> heronIter(9,1)
3.023529411764706
>>> heronIter(9,0.1)
3.00009155413138
>>> heronIter(9,1e-10)
3.0
Aufgabe: Summe von Zahlenbereichen
Mit Zählschleife:
def sum_from_to(n,m):
sum = 0
for i in range(n,m+1):
sum = sum + i
return sum
Mit bedingter Schleife:
def sum_from_to(n,m):
sum = 0
i = n
while i <= m:
sum = sum + i
i = i + 1
return sum
Die Variante mit Zählschleife ist weniger fehleranfällig, weil die Manipulation der Zahlvariablen i automatisch geschieht und keine Gefahr besteht, dass die Schleife versehentlich nicht terminiert.
Bonusaufgabe: Binärdarstellung positiver Zahlen
def binary(n):
bin = ""
while n > 0:
bin = str(n % 2) + bin
n = n // 2
return bin
Aufgabe: Eingaben verarbeiten
Die Eingabezahlen lesen wir mit der Funktion get_int(), die eine Eingabeaufforderung als Parameter erhält und als Ergebnis eine eingelesene Zahl liefert. Dabei wird so lange nach Eingaben gefragt, bis eine gültige Zahl eingegeben
wird.
def get_int(aufforderung):
valid = False
while not valid:
eingabe = input(aufforderung)
if eingabe.isnumeric():
zahl = int(eingabe)
valid = True
else:
print("Ungültige Eingabe!")
return(zahl)
Das folgende Programm liest zwei ganze Zahlen ein und vergleicht sie der Größe nach.
min = get_int("Gib eine ganze Zahl ein: ")
max = get_int("Gib noch eine ganze Zahl ein: ")
if min > max:
num = min
min = max
max = num
if min == max:
print("Die eingegebenen Zahlen sind gleich.")
else:
print(str(max) + " ist größer als " + str(min) + ".")
Hier ist eine Beispiel-Interaktion mit diesem Programm.
Gib eine ganze Zahl ein: zwölf
Ungültige Eingabe!
Gib eine ganze Zahl ein: 12
Gib noch eine ganze Zahl ein: 8
12 ist größer als 8.
Bonusaufgabe: Stein, Schere, Papier
Das Programm zum Spielen von “Stein, Schere, Papier” liest eine Benutzereingabe und wählt dann entsprech um zu gewinnen.
s = input("Stein, Schere oder Papier? ")
while s == "Stein" or s == "Schere" or s == "Papier":
if s == "Stein":
print("Ich hatte Papier genommen. Gewonnen!")
if s == "Schere":
print("Ich hatte Stein genommen. Gewonnen!")
if s == "Papier":
print("Ich hatte Schere genommen. Gewonnen!")
s = input("Stein, Schere oder Papier? ")
Das Programm terminiert, sobald etwas anderes als Stein, Schere
oder Papier eingegeben wird.
Aufgabe: Gängige Fehler
Die Funktion
def is_small_prime(n):
if n == 2 or 3 or 5 or 7:
return True
else:
return False
liefert bei jedem Aufruf den Wert True zurück. Beabsichtigt ist
hingegen, dass nur für die Eingaben 2, 3, 5 und 7 der Wert True und
sonst der Wert False geliefert wird.
Der Fehler liegt in der Formulierung der Bedingung, die implizit wie folgt geklammert ist.
(n == 2) or 3 or 5 or 7
Der Wert dieses Ausdrucks ist True, falls n gleich 2 ist und sonst
gleich 3. Beide Ergebnisse führen zur Ausführung des then-Zweiges
der bedingten Verzweigung.
Beabsichtigt ist hier jedoch nicht die Oderverknüpfung des Vergleiches
n == 2 mit den Zahlen drei, fünf und sieben sondern die
Oderverknüpfung von Vergleichen der Variable n mit den vier
kleinsten Primzahlen. Diese schreiben wir in python wie folgt.
n == 2 or n == 3 or n == 5 or n == 7
Nach einer entsprechen Korrektur liefert die Funktion is_small_prime()
das beabsichtigte Ergebnis.
Die Funktion
def describe_text(s):
if len(s) >= 10:
print("10 Zeichen oder mehr")
if len(s) > 20:
print("Auch mehr als 20")
else:
print("Weniger als 10 Zeichen")
liefert für ein Argument mit einer Länge zwischen 10 und 20 Zeichen
(z.B. Hallo Welt!) eine widersprüchliche Ausgabe.
10 Zeichen oder mehr
Weniger als 10 Zeichen
Dies ist vermutlich nicht beabsichtigt. Die Einrückung suggeriert,
dass der else:-Zweig zur äußeren bedingten Anweisung gehören sollte
und nicht zur inneren. Wir erreichen dies, indem wir die Einrückung von else: und den zugehörigen Block um eine Position ausrücken.
def describe_text(s):
if len(s) >= 10:
print("10 Zeichen oder mehr")
if len(s) > 20:
print("Auch mehr als 20")
else:
print("Weniger als 10 Zeichen")
Nach dieser Korrektur wird beim obigen Beispiel nur noch die erste Ausgabe erzeugt.
Aufgabe: Zahlenbereiche als Zeichenkette
Die Funktion nums_from_to() liefert eine Zeichenkette durch Leerzeichen getrennter Zahlen.
def nums_from_to(lower,upper):
nums = ""
for i in range(lower,upper):
nums = nums + str(i) + " "
if lower <= upper:
nums = nums + str(upper)
return nums
Die bedingte Anweisung sorgt dafür, dass eine leere Zeichenkette geliefert wird, wenn upper kleiner als lower ist.
Die folge Prozedur verwendet die definierte Funktion um Zahlen in einem abgefragten Bereich auszugeben.
def print_nums():
fro = int(input("Erste Zahl: "))
to = int(input("Letzte Zahl: "))
print(nums_from_to(fro,to))
Wenn die obere Grenze kleiner ist als die untere, erzeugt die Prozedur als Ausgabe des Zahlenbereiches nur eine Leerzeile, weil die Funktion nums_from_to() in dem Fall die leere Zeichenkette zurückliefert und print() einen Zeilenumbruch erzeugt.
Hausaufgabe: Prozeduren definieren
Die Prozedur zum Zeichnen eines Dreiecks gegebener Größe verwet die
Hilfsfunktion repeat(), die eine gegebene Zeichenkette wiederholt
aneinander hängt.
def repeat(times,string):
result = ""
for i in range(0,times):
result = result + string
return result
Mit Hilfe dieser Funktion können wir Dreiecke zeichnen, indem wir zuerst den obersten Stern zeichnen, dann in einer Schleife jeweils zwei Sterne mit wachser Anzahl Leerzeichen schreiben und schließlich eine Zeile nur aus Sternen zeichnen. Ein Sonderfall sind Dreiecke der Größe eins, da sie nur aus dem ersten Stern bestehen.
def put_dreieck(n):
print("*")
if n > 1:
for i in range(0, n-2):
print("*" + repeat(i," ") + "*")
print(repeat(n,"*"))
Bonusaufgabe: Prozedur definieren
Auch die Prozedur put_hailstone() verwet die Prozedur repeat(). Sie
berechnet die Zahlen gemäß der angegebenen Vorschrift in einer
bedingten Schleife bis eins erreicht wird und gibt den aktuellen Wert
vor und nach jedem Durchlauf als Sterne aus.
def put_hailstone(n):
while n > 1:
print(repeat(n,"*"))
if n % 2 == 0:
n = n // 2
else:
n = 3*n + 1
print(repeat(n,"*"))
Bonusaufgabe: Geschachtelte bedingte Anweisungen
def put23(n)
for i in range(n):
print (str(i) + " " + zwei3(i))
def zwei3(n)
if n % 2 == 0 and n % 3 == 0:
return "geht durch 2 und 3"
else:
if n % 2 == 0:
return "geht durch 2"
else:
if n % 3 == 0:
return "geht durch 3"
else:
return "geht weder durch 2 noch 3"
Aufgabe: Funktionen und Prozeduren beschreiben
Das gezeigte Programm definiert zwei Funktionen (is_divisible() und
is_prime()) und eine Prozedur (print_prime_twins()). Letztere wird am Ende
des Programms mit dem Argument 100 aufgerufen, wodurch alle
Primzahlzwillinge aus Primzahlen kleiner als 100 ausgegeben werden.
Die Funktion is_divisible() hat zwei Parameter n und k und gibt einen
Wahrheitswert zurück, der beschreibt, ob n durch k teilbar ist.
Die Funktion is_prime() hat einen Parameter n. Der Rückgabewert ist ein
Wahrheitswert, der beschreibt, ob n eine Primzahl ist. Der Rumpf von
is_prime() enthält eine bedingte Schleife, in deren Rumpf mit Hilfe eines
Aufrufs der Funktion is_divisible() getestet wird, ob der Parameter n
durch den Wert der Variablen k teilbar ist. Falls ja, wird durch eine optionale
Anweisung die Ausführung des Funktionsrumpfes beendet und False als Ergebnis
zurückgeliefert. Die Zählvariable k wird durch die Zuweisung k = 2
initialisiert und so lange erhöht, bis ihr Quadrat den Parameter n erreicht
oder übersteigt. Auf diese Weise wird die Ausführung beim kleinsten gefundenen
Teiler, der größer als eins ist, beendet. Falls die Ausführung des
Funktionsrumpfes nicht innerhalb der Schleife abgebrochen wird, wird zurückgegeben, ob der Parameter n größer als eins ist. Es wird also genau dann
True zurückgeliefert, wenn diese Zahl eine Primzahl ist.
Die Prozedur print_prime_twins() hat einen Parameter to und gibt Paare
n,n+2 von Zahlen aus, die beide Primzahlen sind. Solche Paare heißen
Primzahlzwillinge. Dazu werden im Rumpf der Prozedur in einer Zählschleife
alle Paare n,n+2 bis zu n = to daraufhin getestet, ob beide Zahlen
Primzahlen sind. Ist das der Fall, wird das Zahlenpaar mit Hilfe einer
optionalen Anweisung ausgegeben.
Die Definition von Hilfsfunktionen is_divisible() und is_prime() erhöht die
Lesbarkeit des Programms durch sprechende Namen. Im Fall von is_prime()
ermöglicht die Definition des Primzahltests als Funktion außerdem, diesen im Rumpf der Zählschleife von print_prime_twins() mehrfach mit unterschiedlichen Argumenten aufzurufen, wodurch Code-Duplikation vermieden wird.
Die bedingte Schleife im Rumpf von is_prime() ist eigentlich eine Zählschleife,
die bis zur Quadratwurzel des Parameters n läuft. Da die Abbruchbedingung mit
Hilfe einer for-Schleife nicht so kurz beschrieben werden kann wie hier, kann man die Verwendung einer bedingten Schleife als gerechtfertigt betrachten, obwohl sie es erforderlich macht, die Zählvariable explizit zu initialisieren und zu erhöhen. Wegen der return-Anweisung im Schleifenrumpf kann dieser verlassen werden, bevor die Abbruchbedingung erreicht ist. Solch vorzeitige Beendigung der Ausführung einer Schleife (hier sogar des gesamten Funktionsrumpfes) erschwert das Verständnis des Programms, weil nicht einfach ersichtlich ist, unter welchen Umständen welche Programmteile erreichbar sind. Die Verwendung einer return-Anweisung im Schleifenrumpf ließe sich vermeiden, indem man das Ergebnis des Aufrufs von is_divisible() in einer Variablen speichert und deren Wert in der Schleifenbedingung abfragt, um diese zu beenden, wenn ein Teiler gefunden wurde. Auf diese Weise würde zwar die Abbruchbedingung komplexer, aber nicht die Ausführung der Schleife. Dadurch würde erreicht, dass man allein anhand der Abbruchbedingung erkennen kann, wann die Ausführung der Schleife beendet wird.
12. Programmierung mit Zeichenketten
12.1 Programmierung mit Zeichenketten
Wir haben Zeichenketten bereits mit dem +-Operator aneinander gehängt. In Python können wir Zeichenketten auch mit Zahlen multiplizieren. Dabei wird wie bei der repeat()-Funktion aus dem vorigen Abschnitt eine Zeichenkette eine gegebene Anzahl oft wiederholt:
>>> '*' * 5
'*****'
>>> 5 * '*'
'*****'
Zeilenumbrüche und Tabulatoren können als \n bzw. \t notiert werden. Der folgende Aufruf demonstriert die Verwendung dieser Steuerzeichen.
>>> print(('*\t' * 5 + '\n') * 5)
* * * * *
* * * * *
* * * * *
* * * * *
* * * * *
>>>
In diesem Aufruf wird fünfmal hintereinander die Zeichenkette '*\t' * 5 + '\n' ausgegeben, die ihrerseits fünfmal die Zeichenkette *\t sowie einen Zeilenumbruch enthält.
Um alle sogenannten whitespaces (also Leerzeichen, Tabulator-Zeichen, Zeilenende-Zeichen usw.) am Anfang und am Ende
einer Zeichenkette zu entfernen, können wir .strip() verwenden:
>>> " \t a b c \n ".strip()
'a b c'
Die Funktion len liefert die Anzahl der Zeichen einer Zeichenkette zurück.
>>> len("Hello World!")
12
Einzelne Zeichen konnen durch Angabe eines Index in eckigen Klammern in Zeichenketten referenziert werden. Das erste Zeichen hat dabei den Index 0. Bei Verwendung eines ungültigen Index erhalten wir eine Fehlermeldung.
>>> "Hallo Welt!"[0]
'H'
>>> hello = "Hallo Welt!"
>>> hello[len(hello)-1]
'!'
>>> hello[len(hello)]
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
IndexError: string index out of range
Teilstrings können durch Angabe eines Index für Anfang und Ende in eckigen Klammern extrahiert werden. Die folgenden Aufrufe demonstrieren diese sog. String slices:
>>> "Hallo Welt!"[0:5] # String slice
'Hallo'
>>> "Hallo Welt!"[6:10]
'Welt'
>>> "Hallo Welt!"[10:20]
'!'
Die Angabe des extrahierten Bereiches erfolgt mit [Startwert:Endwert], wobei der Endwert den Index des ersten Zeichens bezeichnet, das nicht mehr extrahiert wird.
Bei Verwendung zu großer Indizes ist das Ergebnis die leere Zeichenkette.
>>> "Hallo Welt!"[100:200]
''
Als Startwert und Endwert können auch negative Zahlen angegeben werden. In diesem Fall wird die Position vom Ende der Zeichenkette bestimmt:
>>> "Hallo Welt!"[-5:-1]
'Welt'
12.1.1 Aufgaben
Aufgabe: Text in Wörter zerlegen
Schreiben Sie eine Prozedur print_words() mit einem Parameter text, die eine Zeichenkette als Argument erwartet und untereinander alle Wörter ausgibt, aus denen die Zeichenkette besteht. Die folgenden Aufrufe demonstrieren die Verwendung der Prozedur.
>>> print_words("4 5 6 7")
4
5
6
7
>>> print_words("Eyes mark the shape of the city")
Eyes
mark
the
shape
of
the
city
12.2 Suche in Zeichenketten
Wir können nun eine Funktion schreiben, die zählt, wie oft ein gegebenes Zeichen in einer Zeichenkette vorkommt:
def count_char(text, char):
count = 0
for index in range(0, len(text)): # len(x) liefert die Länge des Textes x
if text[index] == char:
count = count + 1
return count
Hierzu durchlaufen wir in einer Zählschleife alle Zeichen der Zeichenkette text und erhöhen den Zähler count, wenn wir
das gesuchte Zeichen char finden. Die Zahlvariable index durchläuft die
Indizes dabei mit 0 beginnend.
Hier sind einige Beispielaufrufe:
>>> count_char('Hallo Welt!','l')
3
>>> count_char('Hallo Welt!','!')
1
>>> count_char('Hallo Welt!','x')
0
In Python vermeidet man nach Möglichkeit Index-Variablen und die Iteration über einen Bereich. Stattdessen wird über die Elemente des zu iterierenden Objektes direkt iteriert:
def count_char(text, char):
count = 0
for c in text:
if c == char:
count = count + 1
return count
Die Erzeugung eines Range-Objektes und die Verwendung von Indizes lässt sich meist zu Gunsten eines einfacheren, besser lesbaren Codes vermeiden.
Wenn wir nur daran interessiert sind, ob das Zeichen enthalten ist, aber nicht daran wie oft, können wir die Suche bei Erfolg vorzeitig zu beenden, indem wir eine return-Anweisung in dem Rumpf der Schleife einfügen:
def has_char(text, char):
for index in range(0, len(text)):
if text[index] == char:
return True
return False
Ohne Verwendung eines Index lässt sich die Funktion wie oben vereinfachen:
def has_char(text, char):
for c in text:
if c == char:
return True
return False
Im Fall, dass das Zeichen char im text gefunden wird, wird die Funktion mit Rückgabewert True sofort verlassen und die for-Schleife nicht vollständig durchlaufen. Wird das Zeichen nicht gefunden, läuft die for-Schleife vollständig und die Funktion endet mit der Rückgabe von False
Diese Funktion können wir wie folgt verwenden:
>>> has_char('Hallo Welt!', 'l')
True
>>> has_char('Hallo Welt!', '!')
True
>>> has_char('Hallo Welt!', 'x')
False
Wir können auch nach Teilstrings beliebiger Länge suchen und müssen dazu die selektierte Länge an den gesuchten String anpassen. In diesem Beispiel könnne wir auf den Index nicht verzichten, da wir die Slice-Funktion [:] verwenden müssen:
def has_string(text, string):
for index in range(0, len(text)-len(string)):
if text[index:(index + len(string))] == string:
return True
index = index + 1
return False
Zur Illustration wieder einige Beispiele:
>>> has_string('Hallo Welt!', 'llo')
True
>>> has_string('Hallo Welt!', 'lol')
False
>>> has_string('Hallo Welt!', 'welt')
False
Es wird also Groß- und Kleinschreibung unterschieden.
Schließlich können wir dieses Programm noch so abwandeln,
dass es den ersten Index zurück gibt, an dem der gesuchte
String gefunden wurde (bzw. den Fehlerwert None, falls
er nicht gefunden wird).1
def index_of(text, string):
for index in range(0, len(text)-len(string)):
if text[index:(index + len(string))] == string:
return index
return None
Wieder ein paar Beispielaufrufe zur Illustration:
>>> index_of('Hallo Welt!', 'Hallo')
0
>>> index_of('Hallo Welt!', 'Welt')
6
>>> index_of('Hallo Welt!', 'welt')
Das Ergebnis None des letzten Aufrufs wird in der interaktiven Python-Umgebung nicht angezeigt.
Mit der vordefinierten Funktion open() können wir den
Inhalt von Textdateien einlesen. Dabei erhalten wir ein File-Objekt, das wir mit read() in eine Zeichenkette umwandeln können. Dies ermöglicht es uns, auch in größeren Texten, zum Beispiel in unserem Programm, nach
Zeichenketten zu suchen.
>>> source = open('strings.py').read()
>>> indexOf(source,"def has_string")
365
-
Der Wert
Nonewird in Python dort verwendet, wo kein sinnvoller Wert möglich ist. Viele Programiersprachen stellen ähnliche Werte bereit, die dort z.B.nullodernilheißen. ↩︎
12.3 Lösungen
Aufgabe: Text in Wörter zerlegen
def print_words(text):
i = 0
while i < len(text):
word = ""
while i < len(text) and text[i:i+1] != " ":
word = word + text[i:i+1]
i = i + 1
print(word)
i = i + 1
13. Programmierung mit Listen
13.1 Programmierung mit Listen
Eine Möglichkeit, mehrere Werte zu einem zusammenzufassen, ist durch sogenannte Listen gegeben. In Python werden Listen1 durch eckige Klammern notiert, zwischen die die in Ihnen enthaltenen Werte durch Kommata getrennt geschrieben werden. Die folgenden Beispiele in der Python-Shell demonstrieren den Umgang mit Listen:
>>> [41, 42, 43]
[41, 42, 43]
>>> [41, 42] + [43]
[41, 42, 43]
>>> list = [41, 42, 43]
>>> list[0]
41
>>> list[2]
43
>>> list[0:2]
[41, 42]
>>> list[1:3]
[42, 43]
>>> for e in list:
... print(e)
...
41
42
43
Wir können also mehrere Zahlen in einer Liste zusammenfassen und ähnlich wie bei Zeichenketten Listen mit dem +-Operator verketten und auf einzelne gespeicherte Elemente über einen Index zugreifen.
Die Extraktion von Teil-Listen (sog. List slices) funktioniert genau wie bei den Zeichenketten mit [Startwert:Endwert], wobei der Endwert den Index des ersten List-Elementes bezeichnet, das nicht mehr extrahiert wird.
Wir können auch andere Werte als Zahlen in Listen speichern:
>>> strings = ['Hallo', 'Welt']
>>> bools = [True, False, True]
>>> lists = [[1,2,3], strings, bools, []]
>>> lists
[[1, 2, 3], ['Hallo', 'Welt'], [True, False, True], []]
Das letzte Beispiel zeigt, dass auch Listen selbst wieder
Elemente von Listen sein können. Das letzte Element der definierten Liste lists ist dabei eine leere Liste, also eines ohne Einträge.
Wir können Listen verwenden, um zu berechnende Funktionswerte zum schnelleren Zugriff zu speichern. Zum Beispiel können wir eine Liste factorials anlegen, das alle Fakultäten von 0 bis 10 enthält:
factorials = [None] * 11
factorials[0] = 1
for i in range(1,11):
factorials[i] = i * factorials[i-1]
Zunächst wird eine Liste der Länge 11 erzeugt und dabei alle Elemente als None initialisiert.
Danach wird mit einem sogenannten list-Update an der Position mit dem Index 0 der vorherige Wert mit 1 überschrieben.
Der Rumpf der Zählschleife enthält ein list-Update, mit dem der Wert an dem in der Variablen i gespeicherten Index überschrieben wird. Mit der Schleife werden so die Werte an den Indizes von 1 bis 10 überschrieben.
list-Updates ähneln Zuweisungen, allerdings steht bei ihnen links vom Gleichheitszeichen keine Variable, sondern es wird eine durch einen Index beschriebene Position in einer Liste referenziert.
Nach Ausführung des obigen Programms können wir die gespeicherten Fakultäten in der Liste factorials nachschlagen, statt sie immer wieder neu zu berechnen. Falls wir mehrfach auf dieselben Fakultäten zugreifen wollen, können wir deren wiederholte Berechnung also auf Kosten eines höheren Speicherbedarfs einsparen.
-
In anderen Programmiersprachen werden Listen auch als dynamische Arrays bezeichnet. ↩︎
13.1.1 Aufgaben
Hausaufgabe: Listen-Funktionen
Definieren Sie eine Funktion sum, die eine Liste als Argument erwartet und die Summe der in der Liste enthaltenen Zahlen berechnet. (Gehen Sie davon aus, dass die gegebene Liste nur Zahlen enthält. Sie brauchen diesen Umstand also nicht zu testen.) Der Aufruf sum([4,5,6,7]) soll zum Beispiel das Ergebnis 22 liefern.
Definieren eine Funktion from_to, die zwei Zahlen als Argumente erwartet und eine Liste des so definierten Zahlenbereiches liefert. Der Aufruf from_to(4,7) soll zum Beispiel als Ergebnis die Liste [4,5,6,7] liefern.
Bonusaufgabe: Programmierung mit Listen
Sie stehen in Manhattan, sind in zehn Minuten verabredet, möchten aber nicht zu früh erscheinen. Deshalb wollen Sie einen Spaziergang machen, der genau zehn Minuten dauert. Der Spaziergang ['n','s','n','s','o','w','n','s','n','s'] ist dazu geeignet, wenn Sie von einer Straßenecke zur nächsten genau eine Minute brauchen. Die Buchstaben stehen hier für Himmelsrichtungen, in die Sie nacheinander gehen können. Schreiben Sie eine Funktion is_valid_walk(), die solche Listen als Argument erwartet und einen Wahrheitswert zurückliefert, der angibt, ob der Spaziergang in Frage kommt. Neben der Dauer müssen Sie dazu auch überprüfen, ob Sie anschließend wieder an Ihrem Ausgangspunkt ankommen.
13.2 Suche in Listen
Die folgende Funktion sucht ein gegebenes Element x in einer
Liste a und gibt True aus, falls x in a enthalten ist, und sonst False.
def has_element(a, x):
for e in a: #1
if e == x: #2
return True #3
return False #4
Die folgende Programmtabelle dokumentiert die Ausführung
dieses Programms für die Argumente a = [1,2,3,4,5] und x = 3. Wir verzichten dabei auf die Angabe der Werte für x und a, die sich während der Ausführung nicht ändern:
| PP | e | e == x |
Rückgabewert |
|---|---|---|---|
| #1 | 1 | ||
| #2 | False |
||
| #1 | 2 | ||
| #2 | False |
||
| #1 | 3 | ||
| #2 | True |
True |
Wie wir sehen, durchläuft das Programm nicht das gesamte Feld, sondern bricht ab, wenn das Element gefunden wurde.
13.2.1 Aufgaben
Hausaufgabe: Suche in sortierten Listen
Wir haben zwei Varianten einer Funktion has_element betrachtet, die testet, ob eine gegebene Liste ein gesuchtes Element enthält. Die zweite Variante mit bedingter Schleife bricht die Suche ab, sobald das gesuchte Element gefunden wurde. Im Fall eines aufsteigend sortierten Eingabefeldes, können wir die Suche auch dann abbrechen, wenn wir das Element noch nicht gefunden haben, aber alle weiteren Elemente größer sind als das gesuchte.
Implementieren Sie ein Prädikat is_in_sorted, das eine sortierte Liste als erstes Argument erwartet und diese Idee umsetzt. Dokumentieren Sie dessen Ausführung für die Eingaben a = [2,4,6,8,10] und x = 5 mit einer Programmtabelle.
Aufgabe: Liste von Fibonacci-Zahlen
Schreiben Sie analog zum Programm aus der Vorlesung ein Python-Programm, das ein Liste fibs der ersten 11 Fibonacci-Zahlen berechnet. Die erste Fibonacci-Zahl F(0) ist gleich 0, für die zweite gilt F(1)= 1 und für alle weiteren Fibonacci Zahlen gilt F(i) = F(i-1) + F(i-2).
Aufgabe: Binäre Suche in Listen
Wir können die Listen-Suche im Fall sortierter Listen noch verbessern. Implementieren Sie eine Funktion, die so aufgerufen werden kann wie is_in_sorted und auch das selbe Ergebnis liefert. Berechnen Sie dieses Ergebnis mit einer Teile-und-Herrsche-Suchstrategie, die analog zum Spiel “Zahlenraten” verfährt: In jedem Schritt soll dabei die Größe des durchsuchten Bereichs halbiert werden, bis das Element gefunden wurde oder der Bereich das gesuchte Element nicht mehr enthalten kann. Vergleichen Sie Laufzeiten Ihrer Funktion mit der von is_in_sorted, indem Sie zunächst mit einer Schleife große sortierte Listen erzeugen und dann mit beiden Funktionen die selben Elemente darin suchen.
Bonusaufgabe: Was berechnet dieses Programm?
Beschreiben Sie die Arbeitweise und die Ausgabe dieses Programms, ohne es auszuführen.
p = [True] * 101
p[0] = False
p[1] = False
for i in range(2, 11):
if p[i]:
for j in range(i, 100 // i + 1):
p[i*j] = False
for i in range(0,101):
if p[i]:
print(i)
13.3 Lösungen
Lösungen
Hausaufgabe: Listen-Funktionen
def sum(nums):
sum = 0
for n in nums:
sum = sum + n
return sum
def from_to(lower,upper):
nums = [None] * (upper-lower+1)
for i in range(lower,upper+1):
nums[i-lower] = i
return nums
Bonusaufgabe: Programmierung mit Listen
def is_valid_walk(walk):
if len(walk) != 10:
return False
x = 0
y = 0
for step in walk:
if step == "n":
y = y + 1
if step == "s":
y = y - 1
if step == "o":
x = x + 1
if step == "w":
x = x - 1
return x == 0 and y == 0
Hausaufgabe: Suche in sortierten Listen
Das folgende Programm sucht ein gegebenes element x in einer
sortierten Liste a und bricht die Suche ab, sobald die restlichen
Elemente größer sind als das gesuchte.
def is_in_sorted(a,x):
found = False #1
i = 0 #2
while not found and i < len(a) and a[i] <= x: #3
found = (a[i] == x) #4
i = i + 1 #5
return found #6
Die folgende Programmtabelle:kumentiert die Ausführung der Funktion
für die Argumente a = [2,4,6,8,10] und x = 5.
| PP | found | i | !found | i < a.size | a[i] <= x | Rückgabewert |
|---|---|---|---|---|---|---|
| #1 | False | |||||
| #2 | 0 | |||||
| #3 | True | True | True | |||
| #4 | False | |||||
| #5 | 1 | |||||
| #3 | True | True | True | |||
| #4 | False | |||||
| #5 | 2 | |||||
| #3 | True | True | False | |||
| #6 | False |
Aufgabe: Liste von Fibonacci-Zahlen
Das folgende python-Programm berechnet eine Liste aus Fibonaci-Zahlen, indem es in einer Schleife basierend auf den beiden vorherigen Einträgen vergrößert wird.
n = 10
fibs = [None] * (n+1)
fibs[0] = 0
fibs[1] = 1
for i in range(2, n+1):
fibs[i] = fibs[i-1] + fibs[i-2]
print(fibs)
Es gibt das Liste [0,1,1,2,3,5,8,13,21,34,55] aus.
Aufgabe: Binäre Suche in Listen
Die folgende Funktion sucht mit sogenannter binärer Suche.
def bin_search(a,x):
# Die Grenzen left und right definieren,
# in welchem Bereich noch gesucht werden muss.
# Dieser Bereich wird in jedem Schritt halbiert.
left = 0
right = len(a)
# right ist der erste Index, der nicht mehr betrachtet werden muss.
found = False
while not found and left < right:
i = (left + right) // 2
if a[i] < x:
left = i + 1
# left = i wäre hier falsch,
# da dann z.B. der Aufruf bin_search([0],1) nicht terminiert.
if a[i] > x:
right = i
# right = i - 1 wäre hier falsch,
# da dann z.B. bin_search([0,1],0) False zurück liefern würde.
found = a[i] == x
return found
In jedem Schritt wird der zu durchsuchende Bereich halbiert. Dazu wird zunächst das mittlere Element getestet und dann rechts oder links davon weiter gesucht, falls es nicht das gesuchte Element ist.
Wir können die Laufzeiten von is_in_sorted() und bin_search() mit dem folgenden Programm vergleichen.
from datetime import datetime
from is_in_sorted import is_in_sorted
n = 200_000_000
big = [None] * n
for i in range(0,n):
big[i] = i + 1
print(datetime.now())
print(is_in_sorted(big,n))
print(datetime.now())
print(bin_search(big,n))
print(datetime.now())
Die Funktion is_in_sorted() braucht fast eine halbe Minute, um ein Feld mit
200 Millionen Elementen zu durchsuchen, bin_search() schafft das gleiche in
unter einer Sekunde:
2022-03-08 14:49:15.087615
True
2022-03-08 14:49:41.921407
True
2022-03-08 14:49:41.921445
Bonusaufgabe: Was berechnet dieses Programm?
Das gezeigte Programm gibt alle Primzahlen aus, die kleiner sind als 100. Dazu streicht es gemäß des Siebs des Eratosthenes Vielfache von gefundenen Primzahlen, so dass am Ende nur noch Primzahlen übrig bleiben.
14. Programmierung mit Dictionaries
14.1 Dictionaries
Wir betrachten eine Liste, bei der nur wenige Stellen besetzt sind:
>>> liste = [None,None,None,None,None,None,None,'Hello',None,'World']
>>> for e in liste:
... if e:
... print(e)
...
Hello
World
>>> liste[0]
>>> liste[7]
'Hello'
>>> liste[9]
'World'
>>>
Diese Datenstruktur ist ineffizient hinsichtlich des Speicherbedarfs. Dictionaries bieten eine effizientere Repräsentation:
>>> dict = {7 : 'Hello', 9: 'World'}
>>> dict[7]
'Hello'
>>> dict[9]
'World'
>>> dict[0]
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 0
>>> 0 in dict
False
>>> 7 in dict
True
In einem Dictionary werden Paare aus einem Schlüssel und einem zugewiesenen Wert key:value gespeichert. Dabei tritt jeder Schlüssel (wie ein Index in einer Liste) höchstens einmal auf. Mithilfe eines dict-updates wird ein neues Schlüssel-Wert-Paar in ein Dictionary eingefügt, solange dieser Schlüssel noch nicht enthalten ist, andernfalls wird der alte Wert, der zu dem Schlüssel gehört, durch den neuen Wert ersetzt.
>>> 8 in dict
False
>>> dict[8] = 'schöne'
>>> dict[8]
'schöne'
>>> 8 in dict
True
>>> 7 in dict
True
>>> dict[7]
'Hello'
>>> dict[7] = 'Adios'
>>> dict[7]
'Adios'
Anstelle von Zahlen können auch andere Obkekte verwendet werden, zum Beispiel Zeichenketten:
>>> person = {'Name': 'Müller', 'Gehalt': 2500, 'Abteilung': 'Vertrieb'}
>>> person['Gehalt']
2500
>>> person['Name']
'Müller'
>>>
14.1.1 Aufgaben
Aufgabe: Dictionary-Funktionen
Definieren Sie eine Prozedur print_dict, die ein Dictionary als Argument erwartet und alle Schlüssel-Wert-Paare zeilenweis ausgibt.
Für das Dictionary {'Name': 'Müller', 'Gehalt': 2500, 'Abteilung': 'Vertrieb'} sollte die Ausgabe wie folgt formatiert sein:
Name: Müller
Abteilung: Vertrieb
Gehalt: 2500
Die Reihenfolge der Zeilen darf beliebig sein.
Definieren Sie eine Funktion input_person, die Name, Gehalt und Abteilung von der Tastatur abfragt und ein dictionary wie oben zurückgibt.
Bonusaufgabe: Liste von Dictionaries
Erweitern Sie die Funktion input_person zu input_persons, sodass die Daten mehrerer Personen abgefragt und als eine Liste von Dictionaries zurückgegeben werden.
14.2 Tupel
Tupel … to be written
14.3 Sets
Zur Implementierung von Mengen nutzt man in Python sets.
… tobe written
15. Terme und ihre Auswertung
15.1 Termdarstellungen
In der Informatik wird zwischen verschiedenen Darstellungsebenen von Termen unterschieden. Der gleiche Term kann auf unterschiedliche Weise dargestellt werden und verschiedene Terme können zu demselben Wert ausgewertet werden. Die Darstellung eines Terms wird als seine Syntax bezeichnet, der Wert zu dem er ausgewertet wird, als seine Semantik. Zum Beispiel sind 1 + 2 und 2 + 1 zwei verschiedene Terme mit derselben Semantik. Im folgenden werden wir sehen, dass auch ein und derselbe Term mit unterschiedlicher Syntax dargestellt werden kann.
Eine Möglichkeit, Terme auf unterschiedliche Weise darzustellen, ist es, Klammern zu schreiben, die bereits durch Präzedenzregeln implizit vorgegeben sind. Zum Beispiel sind 3 + math.sqrt(x**2 + 1) und 3 + math.sqrt((x**2)+1) der gleiche Term, da Potenzierung (**) stärker bindet als Addition (+), die zusätzlichen Klammern an der Termstruktur also nichts ändern. Durch vollständige Klammerung kann die Struktur eines Terms ohne Hilfe von Präzedenzregeln eindeutig kenntlich gemacht werden. Eine andere Möglichkeit sind sogenannte Termbäume, wie der folgende, der den obigen Term repräsentiert:
Hier stehen Funktionssymbole oberhalb ihrer Argumente und die Klammerung ist durch die Baumstruktur kenntlich gemacht1.
In Python werden Funktionsnamen wie math.sqrt vor ihren Argumenten notiert (Präfix-Notation) und zweistellige Operatoren wie + werden zwischen ihren Argumenten notiert (Infix-Notation).
Wir können auch Operatoren in Präfix-Notation schreiben:
+(3,math.sqrt(+(**(x,2),1)))
Wenn die Stelligkeit (also die Anzahl der Argumente) aller Funktions- und Operator-Symbole eindeutig festgelegt ist, können wir alle Klammern weglassen, ohne dass die Termstruktur dadurch verloren geht:
+ 3 math.sqrt + ** x 2 1
Da wir die Stelligkeiten aller Funktions- und Operator-Symbole kennen, können wir den zu dieser Darstellung gehörigen Termbaum eindeutig rekonstruieren. Wir können auch umgekehrt die Präfix-Notation aus dem Termbaum ableiten, indem wir zuerst die Wurzel des Baums notieren und dann mit den Argumenten genauso verfahren. Wir notieren also danach die Wurzel des Teilbaums für das erste Argument, dann dessen Argumente und so weiter. Wenn dieser Teilbaum abgearbeitet ist, verfahren wir entsprechend mit den weiteren Argumenten.
Analog zur Präfix-Notation wird auch die Postfix-Notation betrachtet. Diese kann aus dem Termbaum abgeleitet werden, indem die Wurzel jedes Teilbaums nicht vor sondern nach den zugehörigen Argumenten notiert wird. Für das obige Beispiel ergibt sich:
3 x 2 ** 1 + math.sqrt +
Genau wie aus der Präfix-Notation kann auch aus der Postfix-Notation der zugehörige Termbaum anhand der Stelligkeiten rekonstruiert werden.
Die (wie bei der Präfix-Notation) klammerfrei eindeutige Darstellung ist nur ein Vorteil der Postfix-Notation. Der eigentliche Grund für die Relevanz der Postfix-Notation ist, dass sie sich besonders gut eignet, um Terme mit Hilfe einer sogenannten Stackmaschine auszuwerten. Bevor wir uns dem dieser Auswertung zu Grunde liegenden Mechanismus widmen, lernen wir jedoch unsere ersten Datenstrukturen kennen.
-
In der Informatik wachsen Bäume von oben nach unten. ↩︎
15.1.1 Aufgaben
Aufgabe: Termdarstellungen berechnen
Hinweis: Um zu testen, ob ein in einer Variablen term gespeicherter Wert eine Liste ist, können Sie die folgende Notation verwenden: type(term)==list liefert True zurück, wenn term eine Liste ist und ansonsten False.
Definieren Sie drei Python-Funktionen zur Darstellung von Termen. Als Eingabe sollen alle Funktionen Terme erwarten, die als geschachtelte Listen dargestellt sind. Diese Darstellung der Eingabe lässt sich am einfachsten anhand eines Beispiels verdeutlichen. Der Term ((4-2)+((1/2)*3)) wird durch die folgende Liste dargestellt:
term = ["+", ["-", 4, 2], ["*", ["/", 1, 2], 3]]
Jeder Term ist also entweder eine dreielementige Liste oder eine Zahl. Im Fall komplexer Terme ist das erste Listen-Element eine Zeichenkette, die eine binäre Rechenoperation beschreibt. Das zweite und dritte Listen-Element sind jeweils Terme, die die beiden Argumente der Operation darstellen.
Definieren Sie eine Funktion infix, die die geklammerte Infixdarstellung eines so dargestellten Terms als Zeichenkette zurückgibt. Zum Beispiel soll infix(term) mit der obigen Definition für term die vorher gezeigte Infixdarstellung berechnen.
Definieren Sie Funktionen prefix und postfix, die entsprechend die Präfix- und Postfix-Darstellung eines Terms berechnen. Diese Funktionen erwarten wie infix einen als geschachtelte Liste dargestellten Term als Argument, sollen aber keine Zeichenkette sondern eine (nicht geschachteltes) Liste zurückliefern, wie die folgenden Aufrufe zeigen.
>>> prefix(term)
["+", "-", 4, 2, "*", "/", 1, 2, 3]
>>> postfix(term)
[4, 2, "-", 1, 2, "/", 3, "*", "+"]
Aufgabe: Terme rekursiv auswerten
Definieren Sie eine rekursive python-Funktion eval_expr, die eine als Liste dargestellten arithmetischen Ausdruck der Form ["+", ["-", 4, 2], ["*", ["/", 1, 2], 3]] als Argument erwartet und als Ergebnis den Wert des Ausdrucks zurückliefert. Jeder Ausdruck ist also entweder eine dreielementige Liste oder eine Zahl. Im Fall komplexer Ausdrücke ist das erste Listen-Element eine Zeichenkette, die eine binäre Rechenoperation beschreibt. Das zweite und dritte Listen-Element sind jeweils Ausdrücke, die die beiden Argumente der Operation darstellen.
Für den gezeigten Ausdruck soll die Funktion 3.5 zurückliefern.
Hinweis: Um zu testen, ob ein in einer Variablen expr gespeicherter Wert eine Liste ist, können Sie die folgende Notation verwenden: type(expr)==list liefert True zurück, wenn expr eine Liste ist und ansonsten False.
15.2 Schlangen und Keller
Datenstrukturen dienen dazu, mehrere Werte zu einem Ganzen zusammenzufassen. Zwei der einfachsten Datenstrukturen in der Informatik sind sogenannte Schlangen (englisch: queues) und Keller (auch Stapel oder englisch: stacks).
Beide Begriffe darf man wörtlich nehmen: Queues funktionieren wie die Warteschlangen an der Supermarktkasse – wer sich zuerst anstellt, ist auch als Erstes wieder draußen – und Stacks wie der heimische Keller – alles wird obendrauf geworfen, und wenn man das braucht, was ganz unten liegt, muss man alles andere aus dem Weg räumen.
Informatisch formuliert arbeiten Queues nach dem FIFO-Prinzip (first in, first out). Sie stellen Operationen zum Einfügen und Entfernen von Elementen bereit, wobei, wie in einer Warteschlange, ein Element erst dann entfernt werden kann, wenn alle vor ihm eingefügten Elemente entfernt wurden.
Stacks arbeiten nach dem LIFO-Prinzip (last in, first out). Elemente können auf einem Stack abgelegt und von diesem
entnommen werden, wobei immer nur das zuletzt abgelegte Element entnommen werden kann. Die Operation zum Ablegen eines Elements auf dem Stack heißt traditionell push, die zum
Entnehmen des zuletzt abgelegten Elements heißt pop.
Das folgende Beispiel veranschaulicht die Arbeitsweise eines Stacks anhand einiger Beispielaufrufe dieser Operationen:
push(3) push(4) pop() push(7) pop() pop()
leerer 4 7 3
Stack 4 ↑ 7 ↑ ↑
↓ 3 3 3 3 3
_____ _____ _____ _____ _____ _____ _____
Zu Beginn ist der Stack leer. Dann wird mit push(3) das Element 3 auf den Stack gelegt. Als Nächstes wird mit push(4) ein weiteres Element oben auf den Stack gelegt, welches dann mit pop() wieder entfernt wird. Die Operation pop() benötigt kein Argument, da immer nur das oberste Element entfernt werden kann. Im Anschluss werden noch die Operationen push(7), pop() und noch einmal pop() ausgeführt, wonach der Stack wieder leer ist.
Im Folgenden werden wir Stacks auch horizontal notieren. Das obige Beispiel sähe in dieser Schreibweise so aus:
| # push(3)
3 | # push(4)
3 4 | # pop()
3 | # push(7)
3 7 | # pop()
3 | # pop()
|
Der Stack ist zu Beginn und am Ende leer und neue Elemente werden rechts neben schon existierende eingefügt.
15.3 Termauswertung einer Stackmaschine
Stacks können verwendet werden, um beliebige Terme in Postfix-Notation automatisch auszuwerten. Bevor Stacks entdeckt wurden, war unklar, wie Terme mit unbegrenzter Schachtelungstiefe automatisch auszuwerten sind. Tatsächlich war in frühen Programmiersprachen die Schachtelungstiefe für Klammerung begrenzt. Erst mit der Entdeckung von Stacks konnten solche Begrenzungen aufgehoben werden.
Zur Auswertung eines Terms in Postfix-Notation wird dieser rechts neben einen leeren Stack geschrieben. Als Beispiel betrachten wir die Auswertung unseres Beispielausdrucks für die Variablenbelegung x = 0.
| 3 0 2 ** 1 + math.sqrt +
Ist das am weitesten links stehende Symbol wie hier eine Konstante, wird es mit der Operation push auf den Stack gelegt und aus der Termdarstellung entfernt:
| 3 0 2 ** 1 + math.sqrt + # push(3)
3 | 0 2 ** 1 + math.sqrt + # push(0)
3 0 | 2 ** 1 + math.sqrt + # push(2)
3 0 2 | ** 1 + math.sqrt +
Ist das am weitesten links stehende Symbol wie hier ein Funktions- oder Operator-Symbol, werden zuerst Elemente entsprechend der Stelligkeit des Symbols mit pop() vom Stack entfernt und dann das Ergebnis der Anwendung der zum Symbol gehörigen (hier mathematischen) Funktion auf diese Argumente mit push() oben auf den Stack gelegt.
3 0 2 | ** 1 + math.sqrt + # pop(); pop(); push(0**2)
3 0 | 1 + math.sqrt +
Während ** in der Termdarstellung ein Funktionssymbol
(Syntax) bezeichnet, bezeichnet es im Argument von push() die
zugehörige mathematische Funktion zur Potenzierung (Semantik). Entsprechend steht nach der Abarbeitung dieses Schrittes
der Wert 0**2 = 0 oben auf dem Stack. Nun verfahren wir
gemäß dieser Regeln, bis der komplette Term abgearbeitet ist
und auf dem Stack nur noch ein einziger Wert steht.
3 0 | 1 + math.sqrt + # push(1)
3 0 1 | + math.sqrt + # pop(); pop(); push(0+1)
3 1 | math.sqrt + # pop(); push(math.sqrt(1))
3 1 | + # pop(); pop(); push(3+1)
4 |
Die Auswertung des Terms 3 + Math.sqrt(0**2 + 1) endet also mit dem Ergebnis 4.
15.3.1 Aufgaben
Hausaufgabe: Term darstellen und mit Stackmaschine auswerten
Geben Sie sowohl die Termbaumdarstellung als auch die Präfix- und Postfix-Darstellung des folgenden Ausdrucks an. Berücksichtigen Sie dabei implizite Präzedenzen wie in python.
2-1 > 0 and Math.sin(x) < 0.01
Wählen Sie dann eine geeignete Darstellung und werten Sie den Ausdruck für die Variablenbelegung x = 3.14 mit einer Stackmaschine aus.
Aufgabe: Stackmaschine programmieren
In dieser Aufgabe sollen Sie den Algorithmus zur Auswertung arithmetischer Ausdrücke in Postfix-Darstellung mit einer Stackmaschine in python implementieren.
Dazu ist es nützlich, dass die Stack-Operationen append1 und pop für Listen in python definiert sind, wie die folgenden Beispielaufrufe zeigen:
>>> stack = []
>>> stack.append(42)
>>> stack
[42]
>>> stack.append(43)
>>> stack
[42,43]
>>> stack.pop()
43
>>> stack
[42]
Für eine definierte Liste stack (das auch anders heißen kann) ist also stack.append eine Prozedur, die sie Liste stack derart verändert, dass das übergebene Argument das neue letzte Element der Liste ist. Die Funktion stack.pop liefert das letzte Element von stack zurück und entfernt es aus der Liste stack.
Definieren Sie eine Funktion eval_postfix(expr), die einen Ausdruck in Postfix-Darstellung als Argument erwartet und das Ergebnis der Auswertung dieses Ausdrucks zurückliefert. Verwenden Sie intern eine Liste als Stack und manipulieren Sie diese entsprechend des Algorithmus aus der Vorlesung.
Der Ausdruck in Postfix-Darstellung kann ebenfalls als Liste dargestellt werden. Zum Beispiel kann der Ausdruck 1 1 + 1 - in python als Liste von Zahlen und Zeichenketten dargestellt werden, nämlich als [1, 1, '+', 1, '-'].
Zur Verarbeitung dieser Darstellung sind die folgenden vordefinierten Operationen hilfreich.
-
Für einen beliebigen Python-Wert
xlieferttype(x)==streinen Wahrheitswert zurück, der angibt, ob es sich beixum eine Zeichenkette handelt. Diese Operation können Sie verwenden, um Zahlen von Rechenoperationen im gegebenen Ausdruck zu unterscheiden. -
Für eine nicht-leere Liste
alieferta.pop(0)das erste Element zurück und entfernt es gleichzeitig ausa(pop(0)ist also wiepop(), aber nicht am Ende sondern am Anfang der Liste). Diese Operation können Sie verwenden, um das nächste Element aus dem Ausdruck herauszuholen.
Der Aufruf eval_postfix([1, 1, '+', 1, '-']) soll das Ergebnis 1 liefern. Gehen Sie davon aus, dass nur gültige Postfix-Darstellungen als Argument übergeben werden. Ihre Implementierung soll mindestens die im Beispiel verwendeten binären Operatoren + und - erlauben.
-
In Python ist die push-Operation für Listen als
appenddefiniert. ↩︎
15.4 Tabellenkalkulation
Office-Programme zur Tabellenkalkulation bieten die Möglichkeit, den Inhalt von Tabellenfeldern mit Hilfe von Termen automatisch berechnen zu lassen. Die Rolle von Variablen spielen Feldbezeichner wie A1, B7 und so weiter.
Wir können zum Beispiel die Formel =(2-1 > 0) AND (SIN(A1) < 0.01) in das Feld A2 eintragen1 , die den entsprechenden Term ausrechnet. Schreiben wir den Wert 3.14 in das Feld A1, so wird in das Feld A2 automatisch der Wert TRUE eingetragen.
-
Die Syntax variiert je nach verwendeter Software ↩︎
15.4.1 Aufgaben
Hausaufgabe: Tabellenkalkulation anwenden
Definieren Sie in einem Tabellenkalkulationsprogramm Ihrer Wahl eine Tabelle, die es ermöglicht
- die Kreisfläche zu einem gegebenen Radius
- sowie die Lösungen einer quadratischen Gleichung der Form \(a\cdot x^2 + b\cdot x + c = 0\)
zu berechnen. Informieren Sie sich mit der Hilfe-Funktion der gewählten Software oder im Internet darüber, welche Funktionen vordefiniert sind und wie Sie für die Aufgabenstellung geeignete Funktionen verwenden können.
15.5 Lösungen
Lösungen
Aufgabe: Termdarstellungen berechnen
Termdarstellungen lassen sich am einfachsten mit rekursiven Definitionen erzeugen:
def infix(term):
if type(term)==list:
return "(" + infix(term[1]) + term[0] + infix(term[2]) + ")"
else:
return str(term)
def prefix(term):
if type(term)==list:
return [term[0]] + prefix(term[1]) + prefix(term[2])
else:
return [term]
def postfix(term):
if type(term)==list:
return postfix(term[1]) + postfix(term[2]) + [term[0]]
else:
return [term]
Im rekursiven Fall werden die Ergebnisse der beiden rekursiven Aufrufe jeweils an geeigneter Stelle mit dem Operationssymbol des Terms verknüpft.
Aufgabe: Terme rekursiv auswerten
Die Funktion eval_expr testet, ob das Argument eine Liste ist. Wenn nicht, ist der Ausdruck bereits vollständig ausgewertet (weil er z.B. eine Zahl ist) und kann unverändert zurückgegeben werden. Im Fall einer Liste setzen wir vorraus, dass das erste Element eine Rechenoperation mit genau zwei Argumenten ist, die als zweites und drittes Element in der Liste stehen. Wir berechnen mit rekursiven Aufrufen zunächst die Werte der Argument-Ausdrücke und übergeben diese dann an die Funktion eval_op, die die Rechenoperation auf die Argumente anwendet.
def eval_expr(expr):
if type(expr)==list:
return eval_op(expr[0], eval_expr(expr[1]), eval_expr(expr[2]))
else:
return expr
Die Funktion eval_op testet, welche Operation als erstes Argument übergeben wurde, verknüpft entsprechend das zweite Argument mit dem dritten und liefert das Ergebnis zurück.
def eval_op(op, x, y):
if op == "+":
return x + y
if op == "-":
return x - y
if op == "*":
return x * y
if op == "/":
return x / y
Mit diesen Definitionen liefert der obige Aufruf das Ergebnis 3.5.
Hausufgabe: Term darstellen und mit Stackmaschine auswerten
Der Ausdruck 2-1 > 0 and Math.sin(x) < 0.01 entspricht dem folgenden Termbaum.
and
/ \
> <
/ \ / \
- 0 sin 0.01
/ \ |
2 1 x
Die Präfixdarstellung ist and > - 2 1 0 < sin x 0.01.
Die Postfixdarstellung ist 2 1 - 0 > x sin 0.01 < and.
Letztere eignet zur Auswertung mit einer Stackmaschine. Für x = 3.14 ergibt sich die folgende Auswertung.
Stack Ausdruck
------------------- ------------------------------
2 1 - 0 > 3.14 sin 0.01 < and
2 1 - 0 > 3.14 sin 0.01 < and
2 1 - 0 > 3.14 sin 0.01 < and
1 0 > 3.14 sin 0.01 < and
1 0 > 3.14 sin 0.01 < and
True 3.14 sin 0.01 < and
True 3.14 sin 0.01 < and
True 0.002 0.01 < and
True 0.002 0.01 < and
True True and
True
Das Ergebnis der Auswertung ist also True.
Aufgabe: Stackmaschine programmieren
Die Funktion eval_postfix manipuliert in einer bedingten Schleife einen Stack, solange der gegebene Ausdruck noch Einträge enthält. In jedem Schleifendurchlauf wird dem Ausdruck ein Element entnommen. Zahlen werden aus dem Ausdruck auf den Stack geschoben. Wenn das nächste Element des Ausdrucks ein Operator (also eine Zeichenkette) ist, werden zwei Elemente vom Stack genommen und mit dem Operator verknüpft. Dabei müssen wir das zweite Argument zuerst vom Stack nehmen, da es diesem vorher als zweites hinzugefügt wurde (für die Addition spielt die Reihenfolge der Argumente keine Rolle, für die Subtraktion aber sehr wohl). Wenn das Argument ein gültiger Ausdruck in Postfix-Darstellung war, enthält der Stack nach Abarbeitung der Schleife genau ein Element, das wir als Ergebnis zurückliefern.
def eval_postfix(expr):
stack = []
while len(expr) > 0:
elem = expr.pop(0)
if type(elem)==str:
y = stack.pop()
x = stack.pop()
stack.append(eval_op(elem, x, y))
else:
stack.append(elem)
return stack.pop()
Diese Implementierung verwendet eine Hilfsfunktion evalOp, die eine binäre Operation und zwei Argumente übergeben bekommt und das Ergebnis der Anwendung der Operation auf die Argumente zurückliefert.
def eval_op(op, x, y):
if op == "+":
return (x+y)
if op == "-":
return (x-y)
Wir verwenden hier mehrere optionale return-Anweisungen (statt geschachtelter bedingter Verzweigungen) um anzudeuten, dass alle Operationen gleichberechtigt sind.
16. Reguläre Ausdrücke
17. Syntaxbeschreibung mit (E)BNF
17.1 Syntax arithmetischer Ausdrücke
Mit Hilfe einer Syntaxbeschreibung in BNF können wir, wie das folgende Beispiel zeigt, formal festlegen, welche Zeichenketten vollständig geklammerten arithmetischen Ausdrücken in Python-Schreibweise entsprechen. Üblicherweise beginnen Nichtterminalsymbole mit Großbuchstaben und Terminalsymbole sind zwischen Hochkommata notiert.
Exp ::= Var
| Val
| '(' Exp Op Exp ')'
| Fun '(' Exps ')'
Var ::= 'x' | 'y' | 'z'
Val ::= Num | '-' Num
Num ::= Digit | Digit Num
Digit ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
Op ::= '+' | '-' | '*' | '/' | '**'
Fun ::= 'sqrt' | 'sin' | 'cos'
Exps ::= Exp | Exp ',' Exps
Die Ableitungsregeln einer BNF geben für jedes Nichtterminalsymbol hinter dem Zeichen ::= an, wie dieses abgeleitet werden kann. Alternative Ableitungsmöglichkeiten werden dabei durch einen senkrechten Strich | getrennt.
Aus einer BNF kann man die in der beschriebenen Sprache enthaltenen Wörter schrittweise ableiten. Dazu beginnt man mit einem Nichtterminalsymbol und ersetzt schrittweise Nichtterminalsymbole durch eine mögliche Ableitung, bis alle Nichtterminalsymbole ersetzt sind. Zum Beispiel zeigt die folgende Ableitung, dass (sqrt(((x**2)+1))/x) ein Wort in der beschriebenen Sprache vollständig geklammerter arithmetischer Ausdrücke ist, da wir es aus dem Nichtterminalsymbol Exp ableiten können:
Exp
(Exp Op Exp)
(Exp/Exp)
(Exp/Var)
(Exp/x)
(Fun(Exps)/x)
(sqrt(Exps)/x)
(sqrt(Exp)/x)
(sqrt((Exp Op Exp))/x)
(sqrt((Exp+Exp))/x)
(sqrt((Exp+Val))/x)
(sqrt((Exp+Num))/x)
(sqrt((Exp+Digit))/x)
(sqrt((Exp+1))/x)
(sqrt(((Exp Op Exp)+1))/x)
(sqrt(((Exp**Exp)+1))/x)
(sqrt(((Exp**Val)+1))/x)
(sqrt(((Exp**Num)+1))/x)
(sqrt(((Exp**Digit)+1))/x)
(sqrt(((Exp**2)+1))/x)
(sqrt(((Var**2)+1))/x)
(sqrt(((x**2)+1))/x)
Wie wir sehen, kann eine solche Ableitung aufwendig werden, insbesondere deshalb, weil sich von einem Schritt zum nächsten nur wenig ändert und der Rest des bisher abgeleiteten Wortes unverändert übernommen werden muss. Statt Ableitungen wie oben gezeigt zu notieren, können wir sie auch mit einem sogenannten Ableitungsbaum darstellen. Zum Beispiel beschreibt der folgende Ableitungsbaum die Ableitung des Wortes (3+x) aus dem Nichtterminalsymbol Exp. Hierbei sind Nichtterminalsymbole in abgerundete und Terminalsymbole in eckige Kästen gesetzt.
Die Wurzel des Ableitungsbaums ist mit dem Nichtterminalsymbol Exp beschriftet, aus dem das Wort (3+x) abgeleitet wird.
Im Allgemeinen bilden die Nichtterminalsymbole die inneren Knoten des Baums. Die Kindknoten eines inneren Knotens entsprechen der rechten Seite der Regel, die im entsprechenden Ableitungsschritt angewendet wurde. So hat die Wurzel des gezeigten Ableitungsbaums fünf Kinder, die der rechten Seite der als Erstes angewendeten Regel Exp ::= '(' Exp Op Exp ')' entsprechen.
Die Blätter des Ableitungsbaums sind mit Terminalsymbolen beschriftet. Das abgeleitete Wort ergibt sich, indem man die Blätter des Baums (die sogenannte Front) von links nach rechts liest. Hier ergibt sich das Wort (3+x).
17.1.1 Aufgaben
Aufgabe: Syntaktische Ableitung arithmetischer Ausdrücke
Geben Sie einen Ableitungsbaum an, der zeigt, dass das Wort (sqrt(((x**2)+1))/x) aus dem Nichtterminalsymbol Exp der angegebenen BNF abgeleitet werden kann. Können Sie auch das Wort (sqrt((x**2)+1)/x) ableiten? Geben Sie gegebenenfalls einen Ableitungsbaum an oder argumentieren Sie, warum dies nicht möglich ist.
Aufgabe: Syntaktische Beschreibung logischer Ausdrücke
Definieren Sie eine BNF für vollständig geklammerte logische Ausdrücke und geben Sie ein Wort an, das von dieser beschrieben wird. Geben Sie den zugehörigen Ableitungsbaum an, der jede Regel Ihrer BNF mindestens einmal verwenden sollte.
Hinweis: Für arithmetische Teilausdrücke logischer Ausdrücke können Sie auf die BNF für arithmetische Ausdrücke verweisen ohne sie zu wiederholen.
17.2 Syntax von Palindromen
Der Formalismus BNF ist ein universeller Formalismus zur Beschreibung von Sprachen, also nicht nur zur Beschreibung arithmetischer Ausdrücke geeignet. Als weiteres Beispiel einer mit BNF beschriebenen Sprache betrachten wir die Spache der Palindrome.
Ein Palindrom ist ein Wort, das von vorne und von hinten gelesen gleich ist. Beispiele sind otto, rentner, oder (wenn wir Satz- und Leerzeichen sowie Groß- und Kleinschreibung vernachlässigen) O Genie, der Herr ehre Dein Ego. Die folgende BNF beschreibt formal die Sprache der Palindrome über dem Alphabet {a,...,z}.
Pali ::= 'a' Pali 'a' | ... | 'z' Pali 'z' | 'a' | ... | 'z' | ''
Die drei Punkte gehören hierbei nicht zum Formalismus einer Syntaxbeschreibung in BNF. Sie symbolisieren ausgelassene Regeln, die wir streng genommen alle notieren müssten. Die letzte Regel erlaubt es, das Nichtterminalsymbol Pali zum leeren Wort, also dem Wort, das keine Zeichen enthält, abzuleiten. Dadurch wird es möglich, auch Palindrome mit gerader Anzahl Buchstaben abzuleiten.
Als Beispiel leiten wir das Wort otto aus dem Nichtterminalsymbol Pali ab:
17.3 Erweiterte Backus-Naur-Form (EBNF)
Bei der formalen Spezifikation von Sprachen mit Hilfe der BNF fällt auf, dass häufig ähnliche Konstruktionen auftreten, wie zum Beispiel das optionale Vorkommen von Zeichen oder deren optionale Wiederholung. Um solche Konstruktionen einfacher notieren zu können, wurde die BNF um spezielle Konstrukte zur sogenannten EBNF erweitert.
- Das optionale Vorkommen eines Teilwortes wird durch eckige
Klammern beschrieben. Zum Beispiel können wir die Regeln
für das Nichtterminalsymbol
Valmit Hilfe eckiger Klammern wie folgt vereinfachen:Val ::= ['-'] Num - Die optionale Wiederholung eines Teilwortes wird durch geschweifte Klammern beschrieben. Zum Beispiel können wir
die Regeln für das Nichtterminalsymbol
Expsmit Hilfe geschweifter Klammern wie folgt vereinfachen:Exps ::= Exp {',' Exp} - Schließlich können wir in EBNF den senkrechten Strich für
Alternativen auch innerhalb von durch Klammerung kenntlich gemachten Gruppierungen verwenden. Zum Beispiel
ließe sich das optionale Vorkommen eines Zeichens
astatt als['a']auch als('a' | '')schreiben.
Durch die genannten Erweiterungen wird die Ausdruckstärke nicht verändert: In EBNF lassen sich genau die selben Sprachen beschreiben, die sich auch durch BNF beschreiben lassen.1
-
Die Theoretische Informatik unterscheidet Sprachklassen danach, durch welche Formalismen sie beschrieben werden können. Verschiedene Sprachklassen und zugehörige Mechanismen zu deren Beschreibung werden in der nach Noam Chomsky benannten Chomsky-Hierarchie nach Ausdrucksstärke geordnet. ↩︎
17.4 Syntax von Python-Anweisungen
Nachdem wir einen Teil von Python-Ausdrücken in der BNF beschrieben haben, wollen wir nun Anweisungen beschreiben. Dazu definieren wir eine EBNF mit einem Nichtterminalsymbol Stmt unter Verwendung der vorher definierten Nichtterminalsymbole (insbesondere Exp für arithmetische und BExp für logische Ausdrücke, siehe Übung). Die folgende Grafik veranschaulicht eine Hierarchie von
Python-Anweisungen:
Einfache Anweisungen sind demnach Zuweisungen und Ausgabe-Anweisungen, von der wir exemplarisch die print-Anweisung als mögliche Ableitung des Nichtterminals Stmt
spezifizieren:
Stmt ::= 'print(' (Exp | BExp) ')'
Als Argument kann der print-Anweisung ein beliebiger arithmetischer oder logischer Ausdruck übergeben werden, dessen Wert ausgegeben werden soll. Um dies zu spezifizieren, verwenden wir eine mit Klammern gruppierte Alternative der Nichtterminalsymbole Exp und BExp in der Argumentposition.
Ebenso verfahren wir bei Anweisungen, mit denen der Wert
eines Ausdrucks einer Variablen zugewiesen wird und erweitern
entsprechend die Definition von Stmt:
Stmt ::= ...
| Var '=' (Exp | BExp)
In Python lassen sich mehrere Anweisungen kombinieren, indem man sie untereinander schreibt. Diese Möglichkeit formalisieren wir mit Hilfe des Nichtterminals Stmts:
Stmts ::= Stmt { '\n' Stmt }
\n symbolisiert hier einen Zeilenumbruch.
Hier verwenden wir geschweifte Klammern, um mehrere Anweisungen durch einen Zeilenumbruch trennen zu können. Generell ignorieren wir Leerzeichen bei der Ableitung. Bei der Anwendung dieser Regel zur Ableitung von Anweisungsfolgen mit mehr als einer Anweisung müssen nach unser Definition jedoch Zeilenumbrüche vorhanden sein.
Es bleibt noch die Spezifikation von Kontrollstrukturen, also bedingten Anweisungen und Schleifen.
Bedingte Anweisungen treten in zwei Formen auf, nämlich mit und ohne Alternative hinter dem Schlüsselwort else. Zu ihrer Spezifikation fügen wir eine weitere Regel zur Ableitung aus dem Nichtterminal Stmt hinzu:
Stmt ::= ...
| 'if' BExp ':\n→' Stmts [ '\n←else:\n→' Stmts] '\n←'
Hier verwenden wir BExp für logische Ausdrücke und das eben definierte Nichtterminal Stmts für Anweisungsfolgen. Optionale Alternativen spezifizieren wir mit Hilfe eckiger Klammern. Die Pfeile → und ← symbolisieren die Einrückungen, die in Python vorgeschrieben sind. Sie kommen in Python-Programmen nicht vor, könnten aber in einem Extra-Schritt vor der syntaktischen Analyse anhand der Einrückungen eingefügt werden. Anschließend spielt dann die Einrückung für die Analyse, die stattdessen die Pfeile berücksichtigt, keine Rolle mehr.
Mit Schleifen können wir ähnlich verfahren. Zählschleifen definieren eine Zählvariable, einen Zahlenbereich, den diese durchläuft, und eine Anweisungsfolge, die wiederholt wird.
Stmt ::= ...
| 'for' Var 'in range(' Exp ',' Exp '):\n→' Stmts '\n←'
Wir verwenden entsprechend das Nichtterminal Var für die Zählvariable, Exp für die Grenzen des Zahlenbereiches und Stmts für den Rumpf der Wiederholung.
Schließlich fügen wir noch eine Regel zur Spezifikation bedingter Schleifen hinzu.
Stmt ::= ...
| 'while' BExp ':\n→' Stmts '\n←'
Zusammengefasst ergibt sich die folgende Definition in EBNF zur Beschreibung von Python-Anweisungen:
Stmts ::= Stmt { '\n' Stmt }
Stmt ::= 'print(' (Exp | BExp) ')'
| Var '=' (Exp | BExp)
| 'if' BExp ':\n→' Stmts [ '\n←else:\n→' Stmts] '\n←'
| 'for' Var 'in range(' Exp ',' Exp '):\n→' Stmts '\n←'
| 'while' BExp ':\n→' Stmts '\n←'
17.4.1 Aufgaben
Aufgabe: Alternative Beschreibung arithmetischer Ausdrücke
Betrachten Sie die folgende (alternative) Syntaxbeschreibung in BNF für arithmetische Ausdrücke.
Ausdruck ::= Summand | Ausdruck '+' Summand
Summand ::= Faktor | Summand '*' Faktor
Faktor ::= Ziffer | Variable | '(' Ausdruck ')'
Ziffer ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
Variable ::= 'x' | 'y' | 'z'
Prüfen Sie, ob die folgenden Wörter aus dem Nichtterminalsymbol Ausdruck abgeleitet werden können. Geben Sie dazu entweder einen Ableitungsbaum an oder argumentieren Sie, warum dies nicht möglich ist. In den Ableitungsbäumen dürfen Sie statt der Nichtterminalsymbole deren Anfangsbuchstaben verwenden, also zum Beispiel A statt Ausdruck schreiben.
2*x+32+x*3(2+x)*31+2+3
Bonusaufgabe: Alternative Beschreibung arithmetischer Ausdrücke um Listen-Ausdrücke erweitern
Erweitern Sie die in der vorherigen Aufgabe angegebene Syntaxbeschreibung um weitere Regeln, die Listen und Listenzugriffe beschreiben. Sie dürfen dazu die erweiterte Syntax der Backus-Naur-Form (EBNF) verwenden. Zum Beispiel sollen die folgenden Ausdrücke zusätzlich ableitbar sein.
[1,2+3]x[2][3](x+[3,4])[1+y[5]]
Den Zugriff auf Teillisten (zum Beispiel x[0,2] zur Selektion der ersten beiden Elemente einer Liste x) brauchen Sie nicht zu beschreiben. Achten Sie aber darauf, dass die Beschreibung eindeutig bleibt und der Syntax von Python entspricht. Es also zum Beispiel nur einen Ableitungsbaum für 1+y[5] geben, der dem vollständig geklammerten Ausdruck (1+(y[5])) entspricht.
Aufgabe: Gegebene Syntaxbeschreibung untersuchen
Gegeben sei die folgende Syntaxbeschreibung in BNF:
R ::= '/' S '/'
S ::= E
| E S
E ::= '(' E '|' E ')'
| E '*'
| D
D ::= '0'
| '1'
Untersuchen Sie, ob die Zeichenfolge /0(0|1)*1/ aus dem Nichtterminalsymbol R abgeleitet werden kann. Geben Sie gegebenenfalls einen Ableitungsbaum (oder eine Ableitung) der Zeichenfolge an oder erläutern Sie, warum eine Ableitung nicht möglich ist.
Aufgabe: Syntaxbeschreibung selbst erstellen
Definieren Sie eine (E)BNF, aus der sich alle nichtleeren Zeichenfolgen ableiten lassen, die aus einer beliebigen positiven Anzahl von Buchstaben a-z gefolgt von derselben Anzahl von Ziffern 0-9 bestehen. Es sollen sich also zum Beispiel die Zeichenfolgen a4, ws12 und mat369 ableiten lassen, nicht aber die leere Zeichenfolge, bc1000, pro7, usw.
17.5 Lesetipps
17.6 Lösungen
Aufgabe: Syntaktische Ableitung arithmetischer Ausdrücke
Der folgende Ableitungsbaum zeigt, dass das Wort (sqrt(((x**2)+1))/x)
Aus dem Nichtterminalsymbol Exp der BNF für vollständig geklammerte
arithmetische Ausdrücke ableitbar ist.
Das Wort (sqrt((x**2)+1)/x) wird nicht durch dieselbe BNF
beschrieben, da es ein Klammernpaar weniger enthält als Funktions- und
Operatorsymbole.
Aufgabe: Syntaktische Beschreibung logischer Ausdrücke
Die folgende BNF beschreibt vollständig geklammerte logische
Ausdrücke. Die Nichtterminalsymbole Exp und Var verweisen dabei
auf die BNF für arithmetische Ausdrücke.
BExp ::= 'true' | 'false'
| 'not(' BExp ')'
| '(' BExp BOp BExp ')'
| '(' Exp COp Exp ')'
| Var
BOp ::= 'and' | 'or'
COp ::= '<' | '>' | '<=' | '>=' | '==' | '!='
Diese BNF beschreibt zum Beispiel das Wort (not((false or x)) and (2 < y))
wie der folgende Ableitungsbaum zeigt.
BExp
'(' BExp BOp BExp ')'
'not(' BExp ') 'and' '(' Exp COp Exp ')'
'(' BExp BOp BExp ')' Val '<' Var
'false' 'or' Var Num 'y'
'x' '2'
Aufgabe: Alternative Beschreibung arithmetischer Ausdrücke
Es gibt für alle Wörter Ableitungsbaume, deren Struktur derjenigen der folgenden vollständig geklammerten Ausdrücke entspricht.
((2*x)+3)(2+(x*3))((2+x)*3)((1+2)+3)
Diese Klammerung entspricht auch der in der Mathematik üblichen Klammerung, die Punkt-vor-Strich-Rechnung respektiert und gleichwertige Operatoren linksassoziativ wertet.
Erweiterung um Listen:
Faktor ::= ...
| '[' [ Ausdruck { ',' Ausdruck } ] ']'
| Faktor '[' Ausdruck ']'
Die erste neue Regel ist für Listen-Literale, die zweite für Listen-Zugriffe. Beachtenswert ist bei letzterer die Verwendung von Faktor statt Ausdruck, die sicherstellt, dass zusammengesetzte Listen-Ausdrücke an dieser Position geklammert werden müssen.
Aufgabe: Gegebene Syntaxbeschreibung untersuchen
Ableitung des Wortes /0(0|1)*1/ aus der gegebenen BNF:
R | Regel R -> '/' S '/'
=> '/' S '/' | Regel S -> E S
=> '/' E S '/' | Regel E -> D
=> '/' D S '/' | Regel D -> '0'
=> '/' '0' S '/' | Regel S -> E S
=> '/' '0' E S '/' | Regel E -> E '*'
=> '/' '0' E '*' S '/' | Regel E -> '(' E '|' E ')'
=> '/' '0' '(' E '|' E ')' '*' S '/' | Regel E -> D (2x)
=> '/' '0' '(' D '|' D ')' '*' S '/' | Regel D -> '0'
=> '/' '0' '(' '0' '|' D ')' '*' S '/' | Regel D -> '1'
=> '/' '0' '(' '0' '|' '1' ')' '*' S '/' | Regel S -> E
=> '/' '0' '(' '0' '|' '1' ')' '*' E '/' | Regel E -> D
=> '/' '0' '(' '0' '|' '1' ')' '*' D '/' | Regel D -> '1'
=> '/' '0' '(' '0' '|' '1' ')' '*' '1' '/'
Ableitungsbaum des Wortes /0(0|1)*1/:
R
|
+----+----+
| | |
/ S /
|
+----+----+
| |
E S
| |
D +----+----+
| | |
0 E S
| |
+--+--+ E
| | |
E * D
| |
+---+---+---+---+ 1
| | | | |
( E | E )
| |
D D
| |
0 1
Aufgabe: Syntaxbeschreibung selbst erstellen
Definition einer BNF für Zeichenfolgen aus n Buchstaben gefolgt von n Ziffern (n > 0):
Z ::= A B | A Z B
A ::= 'a' | ... | 'z'
B ::= '0' | ... | '9'
18. Rekursion
18.1 Rekursive Funktionen
In der Mathematik ist die Verwendung von Rekursion zur Definition von Funktionen Gang und Gäbe. Eine typische Definition der Fakultätsfunktion sieht zum Beispiel so aus.
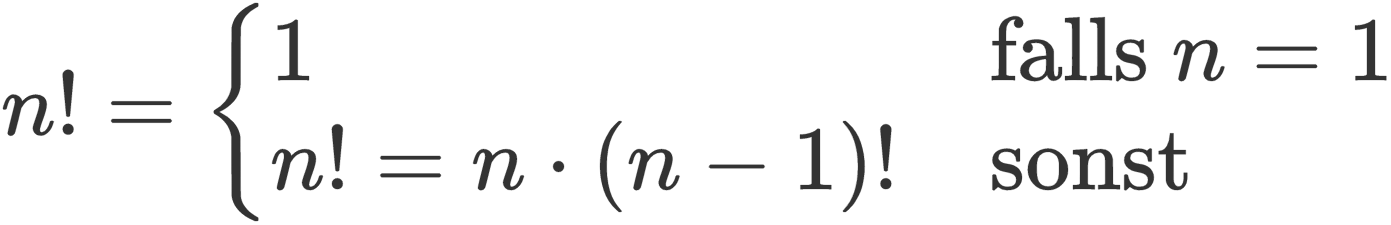
Diese Definition können wir mit Hilfe einer bedingten Verzweigung direkt nach Python übersetzen:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
Falls der Parameter n gleich 1 ist, ist das Ergebnis ebenfalls 1. Falls nicht, wird das Ergebnis mit Hilfe eines rekursiven Aufrufs berechnet.
Rekursive Funktionen sind oft auf diese Weise strukturiert. Mit einer bedingten Verzweigung wird die Abbruchbedingung geprüft, die darüber entscheidet, ob die Berechnung beendet wird oder weiter geht. Im Fall, dass die Berechnung weiter geht, folgt ein rekursiver Aufruf, im Abbruchfall nicht. Falls die Abbruchbedingung nie erfüllt ist, terminiert die Berechnung nicht, genau wie bei einer bedingten Wiederholung, deren Bedingung immer erfüllt ist.
Um die Auswertung rekursiver Funktionen mithilfe von Programmausführungstabellen zu veranschaulichen, muss man für jeden Aufruf eine neue Tabelle anlegen.
Statt einer Funktion, die sich selbst aufruft, können wir auch Gruppen mehrerer rekursiver Funktionen definieren, die sich gegenseitig aufrufen. Die folgenden Definitionen illustrieren diese Technik:
def is_even(n):
if n == 0:
return True
else:
return is_odd(n-1)
def is_odd(n):
if n == 0:
return False
else:
return is_even(n-1)
Die Funktion is_even() liefert True oder False zurück, je nachdem ob die gegebene Zahl n gerade ist oder nicht. Sie verwendet dazu im rekursiven Fall die Funktion is_odd(), die ihrerseits is_even() im rekursiven Fall verwendet. Die Abbruchbedingung beider Funktionen testet, ob das Argument gleich Null ist. Für negative Eingaben definieren diese Funktionen deshalb nicht, was es heißt, gerade oder ungerade zu sein und ein Aufruf mit einem negativen Argument terminiert nicht.
18.1.1 Aufgaben
Aufgabe: Fibonacci-Zahlen rekursiv berechnen
Definieren Sie eine rekursive Funktion fib mit einem Parameter n,
die die n-te Fibonacci-Zahl berechnet. Es soll also fib(0) = 0,
fib(1) = 1 und fib(n+2) = fib(n+1) + fib(n)
gelten. Veranschaulichen Sie die Auswertung des Aufrufs fib(3)
analog zur obigen Auswertung des Aufrufs factorial(3).
Aufgabe: Binärzahlen rekursiv berechnen
Definieren Sie eine rekursive Python-Funktion binary mit einem Parameter n, die die Binärdarstellung der Zahl n als Zeichenkette aus Nullen und Einsen zurückliefert. Gehen Sie davon aus, dass als Argument eine nicht negative ganze Zahl übergeben wird. Zur Konvertierung zwischen Zahlen und Zeichenketten können Sie die Funktionen int und/oder str verwenden. Bei der Suche nach einer Idee für einen rekursiven Berechnungsprozess hilft vielleicht die Beobachtung, dass die Binärdarstellung 110 der Zahl 6 die Binärdarstellung 11 der Zahl 3 enthält.
Dokumentieren Sie die Ausführung des Aufrufs binary(6), indem Sie die Auswertung aller binary-Aufrufe als eigerückte Nebenrechnungen notieren.
Wie viele binary-Aufrufe werden bei der Auswertung von binary(n) in Abhängigkeit von n ausgeführt?
Aufgabe: Rekursive Listen-Funktionen definieren
Geben Sie rekursive Definitionen für die Funktion from_to aus einer früheren Aufgabe an. Zur Erinnerung: from_to erzeugt eine aus Zahlen bestehende Liste anhand übergebener Grenzen (z.B. from_to(4,7) == [4,5,6,7]).
Überlegen Sie sich eine geeignete Abbruchbedingung und geeignete Argumente für rekursive Aufrufe. Geben Sie alternative Definitionen an, wenn Sie unterschiedliche Ideen für rekursive Aufrufe haben, und dokumentieren Sie die Auswertung jeweils mit Hilfe eingerückter Nebenrechnungen.
18.2 Rekursive Prozeduren
Nicht nur Funktionen sondern auch Prozeduren können rekursiv definiert werden. Als Beispiel betrachten wir die folgende Prozedur:
def countdown(n):
print(n)
if n > 0:
countdown(n-1)
Die Prozedur countdown() erwartet eine ganze Zahl als Argument und gibt zunächst die übergebene Zahl aus. Ist sie größer als Null, folgt ein rekursiver Aufruf mit der nächstkleineren ganzen Zahl. Dadurch werden bei Übergabe einer positiven Ganzzahl nacheinander alle ganzen Zahlen von der übergebenen Zahl bis Null ausgegeben, wie der folgende Aufruf zeigt:
>>> countdown(5)
5
4
3
2
1
0
Rekursive Aufrufe müssen nicht immer am Ende einer Definition stehen. Die folgende Prozedur ruft sich selbst auf, bevor ein Wert ausgegeben wird:
def countupto(n):
if n > 0:
countupto(n-1)
print(n)
Wie der Name suggeriert, zählt diese Prozedur aufwärts, denn bevor die übergebene Zahl ausgegeben wird, werden rekursiv alle natürlichen Zahlen bis zur um eins kleineren als die übergebene ausgegeben.
> countupto(5)
1
2
3
4
5
Im Rahmen der Übung sollen Sie damit experimentieren, was passiert, wenn eine Prozedur sich in ihrem Rumpf mehr als einmal selbst aufruft.
18.2.1 Aufgaben
Hausaufgabe: Definition und Analyse rekursiver Prozeduren
Definieren Sie, ohne Schleifen zu verwenden, eine Prozedur print_twice(), die eine Liste als Parameter erwartet und dessen Elemente auf dem Bildschirm ausgibt. Die Elemente sollen einmal der Reihe nach und dann in umgekehrter Reihenfolge ausgegeben werden, wie der folgenden Beispielaufruf veranschaulicht:
>>> print_twice(["A","B","C"])
A
B
C
C
B
A
Betrachten Sie die folgende Prozedurdefinition:
def put_wave(n):
if n > 0:
put_wave(n-1)
print("~~^" * n)
put_wave(n-1)
Beschreiben Sie die Ausgabe von put_wave(n) für beliebige natürliche Zahlen n und erklären Sie, wie sie zustande kommt.
18.3 Rekursion und Schleifen
Wir haben gesehen, dass mit Hilfe von Rekursion, wie mit bedingten Schleifen, nicht terminierende Berechnungen beschrieben werden können. In der Tat sind Rekursion und bedingte Schleifen gleichmächtig, das heißt jedes Programm mit bedingter Schleife kann in eines übersetzt werden, dass statt dieser Rekursion verwendet und umgekehrt. Im folgenden übersetzen wir beispielhaft eine Funktion mit bedingter Schleife in eine rekursive Funktion ohne Schleifen. Die umgekehrte Übersetzung rekursiver Funktionen in Schleifen betrachten wir nicht.
Die folgende Funktion fact_loop() berechnet die Fakultät des Parameters n mit Hilfe einer bedingten Schleife:
def fact_loop(n):
f = 1
i = 1
while i <= n:
f = f * i
i = i + 1
return f
Wir können diese Funktion systematisch in eine rekursive Funktion übersetzen. Dazu definieren wir eine Funktion fact_rec(), die neben dem Parameter n auch noch weitere Parameter für alle vor der Schleife definierten Variablen hat:
def fact_rec(n, f, i):
if i <= n:
f = f * i
i = i + 1
return fact_rec(n, f, i)
else:
return f
oder kürzer:
def fact_rec(n, f, i):
if i <= n:
return fact_rec(n, f*i, i+1)
else:
return f
Im Rumpf dieser Funktion testen wir die Bedingung der Schleife mit einer bedingten Verzweigung. Ist sie erfüllt, so führen wir den Rumpf der Schleife einmal aus und rufen die Funktion dann rekursiv mit geänderten Parametern auf. Ist die Schleifenbedingung nicht erfüllt, bricht die Rekursion ab und wir führen die Anweisungen aus, die nach der ursprünglichen Schleife
kommen, also return f.
Zur Initialisierung der zusätzlichen Parameter führen wir die Anweisungen vor der Schleife aus und rufen dann die Funktion fact_rec() auf.
def fact(n):
f = 1
i = 1
return fact_rec(n, f, 1)
Wir veranschaulichen die Auswertung des Aufrufs fact(4)
analog zur Auswertung von factorial(4) in Kapitel 8.1:
fact(4):
Das Ergebnis von fact(4) ist fact_rec(4, 1, 1)
fact_rec(4, 1, 1):
Die Schleifenbedingung ist erfüllt.
Das Ergebnis von fact_rec(4, 1, 1) ist fact_rec(4, 1*1, 1+1).
fact_rec(4, 1, 2):
Die Schleifenbedingung ist erfüllt.
Das Ergebnis von fact_rec(4, 1, 2) ist fact_rec(4, 1*2, 2+1).
fact_rec(4, 2, 3):
Die Schleifenbedingung ist erfüllt.
Das Ergebnis von fact_rec(4, 2, 3) ist fact_rec(4, 2*3, 3+1).
fact_rec(4, 6, 4):
Die Schleifenbedingung ist erfüllt.
Das Ergebnis von fact_rec(4, 6, 4) ist fact_rec(4, 6*4, 4+1).
fact_rec(4, 24, 5):
Die Schleifenbedingung ist nicht erfüllt.
Das Ergebnis von fact_rec(4, 24, 5) ist 24.
Das Ergebnis von fact(4) ist also 24.
Diesmal notieren wir die rekursiven Aufrufe nicht als verschachtelte Nebenrechnungen, da deren Ergebnisse nicht mehr weiter verrechnet sondern direkt als Ergebnis verwendet werden. Die Zwischenergebnisse werden im zweiten Parameter f von factRec mitgeführt, die Zählvariable im dritten Parameter i.
Die systematische Übersetzung der Fakultätsberechnung mit einer bedingten Schleife in eine rekursive Funktion führt also zu einer alternativen Implementierung, die sich von unserer ursprünglichen rekursiven Fakultätsfunktion sowohl syntaktisch als auch bezüglich ihrer Ausführung unterscheidet.
Die umgekehrte Übersetzung rekursiver Funktionen mit Hilfe von Schleifen ist nicht trivial. Das im folgenden Abschnitt gezeigte Programm lässt sich nicht so einfach ohne Rekursion ausdrücken (möglich ist es aber).
18.4 Die Türme von Hanoi
Als weiteres Beispiel einer rekursiven Prozedur lösen wir das Problem der Türme von Hanoi, das Wikipedia so beschreibt:
Das Spiel besteht aus drei gleich großen Stäben A, B und C, auf die mehrere gelochte Scheiben gelegt werden, alle verschieden groß. Zu Beginn liegen alle Scheiben auf Stab A, der Größe nach geordnet, mit der größten Scheibe unten und der kleinsten oben. Ziel des Spiels ist es, den kompletten Scheiben-Stapel von A nach C zu versetzen.
Bei jedem Zug darf die oberste Scheibe eines beliebigen Stabes unter der Voraussetzung, dass sich dort nicht schon eine kleinere Scheibe befindet, auf einen der beiden anderen Stäbe gelegt werden. Folglich sind zu jedem Zeitpunkt des Spieles die Scheiben auf jedem Feld der Größe nach geordnet.
Die folgende Prozedur ist parametrisiert über die initiale
Anzahl n der zu versetzenden Scheiben und gibt Anweisungen
der Form Lege eine Scheibe von X nach Y aus, wobei für X und Y jeweils einer der Stäbe A, B oder C eingesetzt wird.
def hanoi(n):
hanoi_rec(n, 'A', 'B', 'C')
Um n Scheiben von Stab A über Stab B zu Stab C zu versetzen, können wir, falls n größer als 1 ist, zunächst n-1 Scheiben von A über C nach B versetzen, dann die größte Scheibe von A nach C legen und schließlich die n-1 Scheiben von Stab B über A nach C versetzen. Die Prozedur hanoi_rec() implementiert diese Idee für beliebige Start, Hilfs- und Ziel-Stäbe1
def hanoi_rec(n, source, over, sink):
if n == 1:
print('Lege eine Scheibe von ' + source + ' nach ' + sink + '.')
else:
hanoi_rec(n-1, source, sink, over)
print('Lege eine Scheibe von ' + source + ' nach ' + sink + '.')
hanoi_rec(n-1, over, source, sink)
Im Folgenden veranschaulichen wir die Ausführung des Aufrufs hanoi(3):
hanoi(3)
hanoi_rec(3, 'A', 'B', 'C')
Die Abbruchbedingung ist nicht erfüllt.
hanoi_rec(2, 'A', 'C', 'B')
Die Abbruchbedingung ist nicht erfüllt.
hanoi_rec(1, 'A', 'B', 'C')
Die Abbruchbedingung ist erfüllt.
print('Lege eine Scheibe von A nach C.')
print('Lege eine Scheibe von A nach B.')
hanoi_rec(1, 'C', 'A', 'B')
Die Abbruchbedingung ist erfüllt.
print('Lege eine Scheibe von C nach B.')
print('Lege eine Scheibe von A nach C.')
hanoi_rec(2, 'B', 'A', 'C')
Die Abbruchbedingung ist nicht erfüllt.
hanoi_rec(1, 'B', 'C', 'A')
Die Abbruchbedingung ist erfüllt.
print('Lege eine Scheibe von B nach A.')
print('Lege eine Scheibe von B nach C.')
hanoi_rec(1, 'A', 'B', 'C')
Die Abbruchbedingung ist erfüllt.
print('Lege eine Scheibe von A nach C.')
Die gesamte Ausgabe des Aufrufs ist also folgende:
>>> hanoi(3)
Lege eine Scheibe von A nach C.
Lege eine Scheibe von A nach B.
Lege eine Scheibe von C nach B.
Lege eine Scheibe von A nach C.
Lege eine Scheibe von B nach A.
Lege eine Scheibe von B nach C.
Lege eine Scheibe von A nach C.
Im einzelnen nachzuvollziehen, welche Ausgabe in rekursiven Prozeduren wann erzeugt wird, ist oft trickreich, besonders dann, wenn Ausgaben nach rekursiven Aufrufen erfolgen. Häufig ist es jedoch gar nicht notwendig, die Ausführung rekursiver Programme im Detail nachzuvollziehen. Es genügt oft, das Verhalten rekursiver Aufrufe unabhängig von deren Implementierung zu betrachten.
-
Die Definition lässt sich vereinfachen, denn der
if-Zweig der bedingten Verzweigung ist ein Spezialfall deselse-Zweiges, wenn fürn == 0keine Ausgabe erfolgt. ↩︎
18.4.1 Aufgaben
Aufgabe: Rekursive Programme analysieren
In dieser Aufgabe sollen Sie das folgende Ruby-Programm analysieren.
def zero(n):
if n == 0:
return 0
else:
return zero(zero(n-1))
- Beschreiben Sie die gezeigte Definition unter Verwendung der Begriffe Funktion oder Prozedur, Parameter, Aufruf, Argument, Ergebnis, Rumpf, Rückgabewert, Abbruchbedingung und rekursiv. Bennenen sie außerdem alle Anweisungen mit ihrer korrekten Bezeichnung.
- Veranschaulichen Sie die Auswertung des Aufrufs
zero(3), indem Sie alle rekursiven Aufrufe und zugehörige Ergebnisse in der Reihenfolge ihrer Auswertung notieren. Rücken Sie Unter-Berechnungen entsprechend der Struktur der Auswertung ein. - Welchen Wert liefert ein Aufruf von
zero()mit einer beliebigen natürlichen Zahl als Argument? - Notieren Sie tabellarisch, wie oft
zero()insgesamt (direkt oder indirekt) bei einem Aufrufzero(n)für \(n \in {0,1,2,3,4}\) aufgerufen wird. - Wieviele
zero()-Aufrufe werden zur Auswertungzero(n)für beliebigesnbenötigt?
18.5 Lösungen
Aufgabe: Fibonacci-Zahlen rekursiv berechnen
Fibonacci-Zahlen können wir rekursiv wie folgt berechnen.
def fib(n):
if n <= 1:
return n
else:
return fib(n-1) + fib(n-2)
Die Auswertung von fib(3) erfolgt wie folgt.
`fib(3)` auswerten
`fib(2)` auswerten
`fib(1)` auswerten
Ergebnis ist `1`
`fib(0)` auswerten
Ergebnis is `0`
Ergebnis ist `1 + 0 = 1`
`fib(1)` auswerten
Ergebnis ist `1`
Ergebnis ist `1 + 1 = 2`
Aufgabe: Binärzahlen rekursiv berechnen
def binary(n):
if n <= 1:
return str(n)
else:
return binary(n//2) + str(n%2)
Minimalversion der Dokumentation:
binary(6)
binary(3)
binary(1)
"1"
"1" + "1" = "11"
"11" + "0" = "110"
Bei der Ausführung von binary(n) wird binary() insgesamt l mal aufgerufen, wenn l die nächstgrößere ganze Zahl zum Zweierlogarithmus von n ist.
Aufgabe: Rekursive Listen-Funktionen definieren
Hier sind zwei Varianten der zu definierenden Funktion, die sich darin unterscheiden, welcher Teil des Ergebnisses mit einem rekursiven Aufruf erzeugt wird.
def from_to_tail(lower,upper):
if lower > upper:
return []
else:
return [lower] + from_to_tail(lower+1,upper)
def from_to_init(lower,upper):
if lower > upper:
return []
else:
return from_to_init(lower,upper-1) + [upper]
Die Funktion from_to_tail() erzeugt alle Elemente des Ergebnisses bis auf das erste mit rekursiven Aufrufen.
from_to_tail(3,5)
from_to_tail(4,5)
from_to_tail(5,5)
from_to_tail(6,5)
[]
[5] + [] = [5]
[4] + [5] = [4,5]
[3] + [4,5] = [3,4,5]
Die Funktion from_to_init() hingegen erzeugt alle Elemente bis auf das letzte mit rekursiven Aufrufen.
from_to_init(3,5)
from_to_init(3,4)
from_to_init(3,3)
from_to_init(3,2)
[]
[] + [3] = [3]
[3] + [4] = [3,4]
[3,4] + [5] = [3,4,5]
Als weitere Alternative können wir auf eine Implementierung mit zwei rekursiven Aufrufen angeben, die sowohl die vorderen als auch die hinteren Elemente berechnen.
def from_to_both(lower,upper):
if lower > upper:
return []
else:
mid = (lower + upper) // 2
return from_to_both(lower,mid-1) + [mid] + from_to_both(mid+1,upper)
Hier werden entsprechend zwei rekursive Aufrufe als Nebenrechnungen auf gleicher Ebene ausgewertet.
from_to_both(3,5)
from_to_both(3,3)
from_to_both(3,2)
[]
from_to_both(4,3)
[]
[] + [3] + [] = [3]
from_to_both(5,5)
from_to_both(5,4)
[]
from_to_both(6,5)
[]
[] + [5] + [] = [5]
[3] + [4] + [5] = [3,4,5]
Hausaufgabe: Definition und Analyse rekursiver Prozeduren
Die Prozedur print_twice() bricht ab, wenn die übergebene Liste leer ist und gibt ansonsten das erste Element einmal vor und einmal nach dem rekursiven Aufruf aus. Beim rekursiven Aufruf wird eine Teilliste mit allen restlichen Einträgen übergeben.
def print_twice(a):
if len(a) > 0:
print(a[0])
print_twice(a[1:len(a)])
print(a[0])
Der Aufruf put_wave(n) gibt insgesamt $2^n-1$ Zeilen aus. Die mittlere besteht aus der Zeichenkette "~~^", die n mal hintereinander gehängt ausgegeben wird. Davor und danach werden rekursiv jeweils Wellen der Größe n-1 ausgegeben, so dass insgesamt das folgende Muster entsteht (hier für n=4):
irb> put_wave(4)
~~^
~~^~~^
~~^
~~^~~^~~^
~~^
~~^~~^
~~^
~~^~~^~~^~~^
~~^
~~^~~^
~~^
~~^~~^~~^
~~^
~~^~~^
~~^
Jede zweite Zeile enthält die Zeichenkette "~~^" genau einmal, jede vierte (ab der zweiten) zweimal, jede achte (ab der vierten) dreimal und so weiter.
Aufgabe: Rekursive Programme analysieren
-
Die Funktion
zero()hat einen Parametern. Im Rumpf vonzero()wird der Rückgabewert mit Hilfe einer bedingten Verzweigung bestimmt. Die Abbruchbedingung testet, ob der Wert des Parametersngleich0ist. Falls ja, wird mit Hilfe einerreturnAnweisung der Wert0zurückgegeben. Falls nicht, wirdzero()zunächst rekursiv mit dem Argumentn-1aufgerufen. Danach wirdzero()noch einmal rekursiv mit dem Ergebnis des ersten Aufrufs als Argument aufgerufen. Das Ergebnis des zweiten Aufrufs wird schließlich mit Hilfe einerreturnAnweisung zurückgeliefert. -
Der Aufruf
zero(3)wird wie folgt ausgewertet.
zero(3)
3 == 0 ist false
zero(2)
2 == 0 ist false
zero(1)
1 == 0 ist false
zero(0)
0 == 0 ist true
Ergebnis von zero(0) ist 0
zero(0)
0 == 0 ist true
Ergebnis von zero(0) ist 0
Ergebnis von zero(1) ist 0
zero(0)
0 == 0 ist true
Ergebnis von zero(0) ist 0
Ergebnis von zero(2) ist 0
zero(0)
0 == 0 ist true
Ergebnis von zero(0) ist 0
Ergebnis von zero(3) ist 0
- Jeder Aufruf von
zero()mit einer natürlichen Zahl als Argument liefert als Ergebnis0zurück. - Für $n \in {0,1,2,3,4}$ ergeben sich die folgenden Anzahlen von
zero()-Aufrufen.
n Anzahl Aufrufe
----- ---------------
0 1
1 1+1+1 = 3
2 1+3+1 = 5
3 1+5+1 = 7
4 1+7+1 = 9
- Bei einem Aufruf von
zero(n)mit einer natürlichen Zahl $n$ als Argument werden insgesamt $2n+1$ Aufrufe vonzero()ausgewertet.
19. Sortieren und Effizienz
19.1 Einfache Sortierverfahren und ihre Laufzeit
Im Folgenden entwickeln wir Prozeduren, die eine Liste als Argument erwarten und als Seiteneffekt die Elemente in der gegebenen Liste sortieren. Als Elemente werden wir Zahlen verwenden, die vorgestellten Sortierverfahren sind jedoch meist auch zum Sortieren komplexerer Daten geeignet (sofern diese in einer gewissen Ordnung zueinander stehen).
Selection Sort
Ein einfaches Verfahren zum Sortieren lässt sich umgangssprachlich wie folgt beschreiben:
- Vertausche das erste mit dem kleinsten Element der Liste,
- dann das zweite mit dem kleinsten Element im Teil ohne das erste Element,
- dann das dritte mit dem kleinsten im Teil ohne die ersten beiden
- und so weiter, bis die ganze Liste durchlaufen wurde.
Dieses Verfahren heißt Selection Sort (oder Min Sort), weil die Elemente der Liste nacheinander mit dem Minimum getauscht werden, das aus der Teilliste aller folgenden Elemente ausgewählt wird. Um es in Python zu implementieren, durchlaufen wir in einer Schleife mit fester Anzahl alle Elemente der gegebenen Liste und vertauschen sie mit dem Minimum in der Rest-Liste. Die Funktion min_pos bestimmt dabei die Position des kleinsten Elements und swap vertauscht die Elemente an zwei gegebenen Indizes.
def min_sort(a):
for i in range(0, len(a)):
swap(a, i, min_pos(a, i))
def min_pos(a, start):
pos = start #1
for i in range(start+1, len(a)): #2
if a[i] < a[pos]: #3
pos = i #4
return pos #5
def swap(a, i, j):
temp = a[i]
a[i] = a[j]
a[j] = temp
Diese Funktion durchläuft die Liste ab der gegebenen Position start und merkt sich die Position pos des kleinsten bisher gefunden Elementes, die sie am Ende zurückliefert.
Die folgende Programmtabelle dokumentiert die Ausführung des Ausrufs min_pos([1,2,5,3,4],2):
| PP | pos |
i |
a[i] < a[pos] |
return |
|---|---|---|---|---|
| #1 | 2 | |||
| #2 | 3 | |||
| #3 | True |
|||
| #4 | 3 | |||
| #2 | 4 | |||
| #3 | False |
|||
| #5 | 3 |
Die Korrektheit dieser Funktion können wir mit Hilfe der folgenden Beobachtungen einsehen:
- Vor dem Eintritt in die Schleife ist
pos = start - Nach jedem Schleifendurchlauf ist
posdie Position des kleinsten Elementes inazwischenstartundi. - Nach der Ausführung der Schleife ist
posfolglich die Position des kleinsten Elements zwischenstartund dem Ende der Liste.
Denken wir uns i = start in der Situation vor Eintritt in die Schleife, dann gilt die zweite Bedingung vor, während und nach der Ausführung der Schleife und heißt deshalb Schleifen-Invariante.
Auch von der Korrektheit der Prozedur min_sort können wir uns mit Hilfe einer Invariante überzeugen. Nach jedem Schleifesdurchlauf ist nämlich die Teil-Liste zwischen Position 0 und i sortiert. Insbesondere ist also der Vollendung der Schleife die gesamte Liste sortiert.
Wir können uns dies anhand eines Beispiels veranschaulichen, bei dem wir nacheinander Werte der sortierten Liste notieren, wenn dieses verändert wird. Im nächsten Schritt vertauschte Elemente sind dabei hervorgehoben. Falls nur ein Element hervorgehoben ist, wird es im nächsten Schritt mit sich selbst vertauscht.
- [1, 2, 5, 3, 4]
- [1, 2, 5, 3, 4]
- [1, 2, 5, 3, 4]
- [1, 2, 3, 5, 4]
- [1, 2, 3, 4, 5]
Die Laufzeit der Prozedur min_sort untersuchen wir experimentell, indem wir sie auf Listen unterschiedlicher Größe anwenden. Wir fangen mit einer Liste der Größe 1000 an,
verdoppeln dann dreimal die Listengröße und messen die Zeit, die zum Sortieren benötigt wird:
import time, random
count = 1000
for rounds in range(0, 4):
print(str(count) + ": ")
nums = [None] * count
for i in range(count):
nums[i] = random.randrange(10000)
start = time.process_time()
min_sort(nums)
print(str(time.process_time() - start))
count = 2 * count
Dieses Programm gibt neben der Eingabegröße die zum Sortieren benötigte Zeit in Sekunden aus. Die Ausgabe variiert je nach Rechner auf dem das Programm ausgeführt wird. Auf meinem Laptop ergibt sich:
1000:
0.027022123336791992
2000:
0.11847710609436035
4000:
0.4383370876312256
8000:
1.7466981410980225
Wir können beobachten, dass sich die Laufzeit bei Verdoppelung der Eingabegröße jedesmal ungefähr vervierfacht.
Da die Prozedur min_sort nur Zählschleifen verwendet, hängt ihre Laufzeit nur unwesentlich davon ab, welche Elemente die gegebene Liste enthält. Im Falle einer bereits sortierten Liste wird der Rumpf pos = i der bedingten Anweisung in der Funktion min_pos() niemals ausgeführt, da die Bedingung a[i] < a[pos] immer False ist. Eine Zuweisung wird in der Regel jedoch neben der Vergleichsoperation vernächlässigt, die hier unabhängig von der Eingabe immer gleich häufig ausgeführt wird.
19.1.1 Aufgaben
Aufgabe: Max Sort implementieren
Definieren Sie analog zu min_sort eine Prozedur max_sort, die
eine gegebene Liste sortiert, indem der Reihe nach das
letzte Element durch das größte, das vorletzte durch das
nächstkleinere, u.s.w. ersetzt wird.
Die Liste soll von max_sort aufsteigend sortiert werden.
Vergleichen Sie die Laufzeiten der Prozeduren von min_sort und
max_sort und dokumentieren Sie die Ergebnisse.
19.2 Insertion Sort
Wir lernen nun ein Sortierverfahren kennen, das im Falle einer bereits sortierten Liste schneller ist als Selection Sort. Intuitiv verfahren wir wie beim Aufnehmen einer Hand beim Kartenspiel: Neue Elemente werden der Reihe nach in eine bereits sortierte Teil-Liste eingefügt.
Zur Implementierung in Python durchlaufen wir die Elemente der Liste nacheinander in einer Zählschleife. Wie bei Selection Sort soll nach jedem Durchlauf der Schleife das Teil-Liste von Position 0 bis zur Zählvariable i sortiert sein. Diesmal erreichen wir dies, indem wir das Element an Position i rückwärts in den bereits sortierten Teil einfügen.
def insertion_sort(a):
for i in range(0, len(a)):
insert_backwards(a, i)
Die Prozedur insert_backwards verwendet eine bedingte Schleife, um das Element an der gegebenen Position position so lange mit seinem Vorgänger zu vertauschen, wie es kleiner ist als dieser.
def insert_backwards(a, pos):
while pos > 0 and a[pos] < a[pos-1]:
swap(a, pos, pos-1)
pos = pos - 1
Sobald das einzufügende Element nicht mehr kleiner ist als sein Vorgänger, wird die Schleife beendet. Wir brauchen es dann nicht mehr mit den davor stehenden Elementen zu vergleichen, da diese bereits sortiert sind, das einzufügende Element also nicht kleiner sein kann.
Das folgende Beispiel illustriert die Vertauschungen, die dieser Algorithmus durchführt:
- [1, 2, 5, 3, 4]
- [1, 2, 3, 5, 4]
- [1, 2, 3, 4, 5]
19.2.1 Aufgaben
Aufgabe: Insertion Sort experimentell analysieren
Analysieren Sie die Laufzeit des Insertion Sort Algorithmus experimentell analog zu Selection Sort. Testen Sie den Algorithmus außerdem mit umgekehrt sortieren Listen unterschiedlicher Größe und beschreiben Sie Ihre Beobachtungen. Erzeugen Sie solche Listen mit Hilfe einer selbst definierten Funktion descending. Zum Beispiel soll der Aufruf descending(5) als Ergebnis die Liste [5,4,3,2,1] liefern.
Bonusaufgabe: Insertion Sort rekursiv implementieren
Alternativ zu der gezeigten Implementierung sollen Sie Insertion Sort nun rekursiv implementieren. Definieren Sie dazu eine rekursive Prozedur ins_sort, die zwei Argumente a und to erwartet und die Liste a bis zur Position to sortiert.
Statt einer Zählschleife zu verwenden, deren Invariante besagt, dass ein Anfangsstück bereits sortiert ist, können Sie mit Hilfe eines rekursiven Aufrufs explizit Anfangsstücke sortieren, bevor Sie Elemente mit Hilfe der Prozedur insert_backwards rückwärts einfügen.
19.3 Systematische Laufzeitanalyse
Bisher haben wir die Laufzeit der verwendeten Sortierverfahren experimentell untersucht und einige informelle Beobachtungen angestellt, wie sich die Laufzeit für unterschiedliche Eingaben in Abhängigkeit der Eingabegröße verhält. Im Folgenden kategorisieren wir unsere Beobachtungen und lernen eine Notation kennen, um die Laufzeit von Algorithmen abstrakt zu beschreiben.
Bei Insertion Sort haben wir beobachtet, dass die Laufzeit davon abhängt, ob Elemente bereits vorsortiert sind oder nicht. Bei bereits sortierten Listen verdoppelte sich die Laufzeit bei Verdoppelung der Eingabegröße, bei unsortierten Listen vervierfachte sie sich hingegen.
Tatsächlich ist Insertion Sort bei bereits sortierten Listen am schnellsten und bei umgekehrt sortierten Listen am langsamsten. Es ist deshalb hilfreich, die sogenannte Best-Case- von der Worst-Case-Komplexität zu unterscheiden.
Statt konkreter Laufzeiten gibt man in der Regel eine Funktion an, die das Wachstum der Laufzeit in Abhängigkeit von der Eingabegröße angibt. Im Worst Case für Insertion Sort hat sich die Laufzeit bei Verdopplung vervierfacht, bei Vervierfachung also versechzehnfacht und so weiter. Dies entspricht der Quadratfunktion. Man sagt deshalb: “Die Worst-Case-Komplexität von Insertion Sort ist quadratisch in Abhängigkeit der Größe der sortierten Liste.”
Alternativ sagt man auch: “Die Worst-Case-Komplexität von Insertion Sort ist in \(\mathcal{O}(n^2)\), wobei \(n\) die Größe der sortierten Liste ist.” Die hier verwendete \(\mathcal{O}\) -Notation hat eine genau definierte mathematische Bedeutung, die uns hier aber nicht weiter beschäftigen soll. Sie formalisiert die oben intuitiv beschriebene Angabe der Laufzeit als Funktion der Eingabegröße, hier \(n\) genannt. Dabei haben Algorithmen der Komplexität \(\mathcal{O}(1) = \mathcal{O}(42) = \mathcal{O}(4711)\) die gleiche abstrahierte Laufzeit. Man spricht hier auch von konstanter Laufzeit, weil diese nicht von der Eingabegröße abhängt. Außerdem gilt zum Beispiel \(\mathcal{O}(n^2) = \mathcal{O}(\frac{n^2−n}{2})\) . Die \(\mathcal{O}\)-Notation abstrahiert die Laufzeit also so, dass von Polynomfunktionen nur der Anteil mit dem größten Exponenten von Bedeutung ist. Intuitiv wird dadurch kenntlich gemacht, wie sich die Laufzeit für sehr große Eingaben verhält. Je größer das \(n\), desto weniger fallen die Anteile mit kleinerem Exponenten ins Gewicht. Auch konstante Faktoren (wie \(\frac{1}{2}\) im obigen Beispiel) werden vernachlässigt.
Die folgende Tabelle fasst die Best- und Worst-Case-Laufzeiten der definierten Sortierverfahren zusammen.
| Algorithmus | Best Case (sortiert) | Worst Case (unsortiert) |
|---|---|---|
| Selection Sort | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n^2)\) |
| Insertion Sort | \(\mathcal{O}(n)\) | \(\mathcal{O}(n^2)\) |
Selection Sort hat im Best und im Worst Case die gleiche Komplexität, während Insertion Sort im Best Case besser ist als im Worst Case.
Statt die Komplexitäten experimentell zu ermitteln, können wir sie auch anhand des Programms ermitteln.
Selection Sort verwendet im Wesentlichen zwei geschachtelte Wiederholungen. Die äußere durchläuft einmal die gegebene Liste, wobei in jedem Schritt die innere Wiederholung vom aktuellen Element bis zum Ende läuft, um das kleinste Elemente in diesem Bereich zu finden. Wenn \(n\) die Eingabegröße ist, werden (für \(n > 1\)) insgesamt \((n − 1) + \dots + 1 = \sum\limits_{i=1}^{n-1} i = \frac{(n-1)n}{2} = \frac{n^2-n}{2}\) Vergleiche ausgeführt. Für die Worst-Case-Komplexität von Insertion Sort ergibt sich auf ähnliche Weise dieselbe Anzahl von Vergleichen. Im Best Case wird die innere Schleife von Insertion Sort nicht ausgeführt. In diesem Fall ergeben sich also \(n − 1\) Vergleiche.
Neben Best- und Worst-Case-Komplexität betrachtet man manchmal auch noch Average-Case-Komplexität, also die durchschnittliche Laufzeit gemittelt über alle möglichen Eingaben. Wir werden im nächsten Abschnitt ein Sortierverfahren kennen lernen, dessen Average-Case-Komplexität sich von der Worst-Case-Komplexität unterscheidet.
19.4 Effizientere Sortierverfahren
Wir lernen nun klassische rekursive Sortierverfahren kennen. Auch die Implementierung von Insertion Sort kann mit Hilfe eines rekursiven Aufrufs implementiert werden, nach dem das letzte Element an der richtigen Stelle eingefügt wird. Der Schlüssel zur Effizienz der folgenden Sortierverfahren ist es jedoch, Teil-Listen mit mehreren rekursiven Aufrufen zu sortieren.
Quick Sort
Die Idee von Quick Sort ist es, eine Partitionierung genannte grobe Vorsortierung durch Anwendung rekursiver Aufrufe zu vervollständigen. Die Partitionierung stellt dabei sicher, dass sich alle Elemente, die kleiner sind als ein gegebenes, im vorderen Teil und alle größeren im hinteren Teil befinden. Anschließend werden der vordere und der hintere Teil getrennt voneinander rekursiv sortiert.
Um verschiedene Teile getrennt voneinander sortieren zu können, übergeben wir als zusätzliche Parameter die Grenzen des zu sortierenden Bereiches, die mit den Grenzen der Liste initialisiert werden:
def quick_sort(a):
qsort(a, 0, len(a)-1)
Die rekursive Prozedur qsort implementiert das beschriebene Sortierverfahren:
def qsort(a, l, r):
if l < r:
m = partition(a, l, r)
qsort(a, l, m-1)
qsort(a, m+1, r)
Falls der zu sortierende Bereich mehr als ein Element enthält, wird er zunächst in zwei Bereiche mit der Grenze m partitioniert, die danach rekursiv sortiert werden. Die Prozedur partition ist eine alte Bekannte in neuem Gewand. Wir haben früher bereits ein Programm gesehen, dass eine Liste auf die beschriebene Weise partitioniert. Die folgende Prozedur verallgemeinert dieses Programm so, dass die Grenzen des zu bearbeitenden Bereiches angegeben werden können:
def partition(a, l, r):
m = l
for i in range(l, r):
if a[i+1] < a[l]:
m = m + 1
swap(a, i+1, m)
swap(a, l, m)
return m
Das Element an Position l dient hier als sogenanntes Partitionselement oder Pivot-Element. Die anderen Elemente des Bereiches werden so umsortiert, dass diejenigen Elemente, die kleiner sind als das Partitionselement vor allen stehen, die größer oder gleich sind. Am Ende steht das Partitionselement an Position m und diese Position wird zurückgegeben.
Die folgende Programmtabelle dokumentiert die Ausführung von partition für die Parameter a = [1,2,3,6,7,4,8,5], l = 3 und r = 7.
Partitioniert wird also die Teilliste [6,7,4,8,5] um das Partitionselement 6.
| PP | a |
m |
i |
a[i+1] < a[l] |
Rückgabewert |
|---|---|---|---|---|---|
| #1 | [1,2,3,6,7,4,8,5] |
3 |
|||
| #2 | 3 |
||||
| #3 | False |
||||
| #2 | 4 |
||||
| #3 | True |
||||
| #4 | 4 |
||||
| #5 | [1,2,3,6,4,7,8,5] |
||||
| #2 | 5 |
||||
| #3 | False |
||||
| #2 | 6 |
||||
| #3 | True |
||||
| #4 | 5 |
||||
| #5 | [1,2,3,6,4,5,8,7] |
||||
| #6 | [1,2,3,5,4,6,8,7] |
||||
| #7 | 5 |
Zur Evaluation der Effizienz von Quick Sort rufen wir es mit zufälligen Listen unterschiedlicher Größe auf. Dabei ergeben sich auf meinem Rechner die folgenden Laufzeiten:
1000:
0.002292633056640625
2000:
0.0047588348388671875
4000:
0.010391712188720703
8000:
0.022547483444213867
16000:
0.04721498489379883
32000:
0.10293197631835938
64000:
0.23071861267089844
128000:
0.48602795600891113
256000:
1.0562872886657715
512000:
2.241218328475952
Wir können beobachten, dass sich die Laufzeit bei Verdoppelung der Eingabegröße meist ein wenig mehr als verdoppelt. Die Laufzeit erscheint also fast linear, aber nicht ganz.
Intuitiv können wir uns den Aufwand von Quick Sort verdeutlichen, indem wir den Aufwand für die einzelnen Aufrufe von partition zusammenfassen. Der erste Aufruf durchläuft die Eingabe-Liste einmal komplett um es zu partitionieren. Dann folgen zwei rekursive Aufrufe von qsort, deren partition-Aufrufe die Liste zusammengenommen ebenfalls komplett durchlaufen. Je nach Größe der dabei sortierten Bereiche folgen wieder rekursive Aufrufe, die zusammengenommen das ganze Feld durchlaufen. Um den gesamten Aufwand abzuschätzen ist also die Rekursionstiefe entscheidend, denn sie entscheidet, wie oft die Eingabe-Liste durchlaufen wird.
Im besten Fall wird das Feld vor jedem Rekursionsschritt in gleich große Hälften partitioniert und die Rekursionstiefe ist der Logarithmus der Größe der Eingabe-Liste. Dabei ergibt sich also eine Laufzeit in \(\mathcal{O}(n \cdot \log_2(n)\). Diese Laufzeit ergibt sich auch gemittelt über alle Eingaben also im Durchschnittsfall und erklärt damit unsere experimentellen Beobachtungen.
Im schlechtesten Fall hat die eine Hälfte der Partition die Größe 1 und die andere enthält alle weiteren Elemente. Dieser Fall tritt ein, wenn das Feld sortiert oder umgekehrt sortiert ist. In diesem Fall ist die Rekursionstiefe linear in der Eingabegröße, die Laufzeit also in \(\mathcal{O}(n^2)\).
Die folgende Tabelle fasst die Laufzeiten der bisher diskutierten Sortierverfahren zusammen.
| Algorithmus | Best Case | Worst Case | Average Case |
|---|---|---|---|
| Selection Sort | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n^2)\) |
| Insertion Sort | \(\mathcal{O}(n)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n^2)\) |
| Quick Sort | \(\mathcal{O}(n \cdot \log_2(n))\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n \cdot \log_2(n))\) |
Quick Sort erreicht also gegenüber den bisherigen Verfahren eine wesentliche Verbesserung im Average Case auf Kosten einer unwesentlichen Verschlechterung im Best Case gegenüber Insertion Sort.
Es gibt Sortierverfahren, die die Laufzeit auch im Worst Case verbessern. Im Rahmen der Übung haben Sie die Möglichkeit sich mit ihnen zu befassen.
19.4.1 Aufgaben
Aufgabe: Quick Sort dokumentieren
Welche Aufrufe von partition werden beim Aufruf von
quick_sort(a) mit a = [3,2,1,6,7,4,8,5] in welcher Reihenfolge ausgeführt? Geben Sie an, welchen Wert a vor und nach jedem Aufruf von partition hat.
Aufgabe: Einfache Prozedur zum Sortieren analysieren
Betrachten Sie die folgende Definition in Python.
def simple_sort(a): #0
for i in range(0, len(a)): #1
for j in range(0, len(a)): #2
if a[i] < a[j]: #3
swap(a, i, j) #4
- Verwenden Sie korrekte Fachsprache um die gezeigte Definition zu beschreiben.
- Dokumentieren Sie die Ausführung des Aufrufs
simple_sort([2,1,3])mit Hilfe einer Programmtabelle, die auch eine Spalte für den Parameteraenthält. - Beschreiben Sie den Effekt eines Aufrufs von
simple_sortmit einer Liste von Zahlen. - Beschreiben Sie die Laufzeit von
simple_sortmit Hilfe der O-Notation. - Welche der folgenden Aussagen treffen zu?
- Die Anzahl der bei einem Aufruf von
simple_sortausgeführten Vergleiche hängt nicht von der Reihenfolge der Elemente in der übergebenen Liste ab. - Jedes Paar von Indizes führt zu zwei Vergleichen.
- Direkt nach jedem Durchlauf der äußeren Schleife
- steht das größte Element der gesamten Liste an Index
i. - ist der Bereich bis zum Index
iaufsteigend sortiert.
- steht das größte Element der gesamten Liste an Index
- Die Anzahl der bei einem Aufruf von
Aufgabe: Merge-Sort Funktion implementieren
In dieser Aufgabe lernen Sie ein Sortierverfahren kennen, dessen Laufzeit auch im worst case in \(O(n\cdot log_{2}(n))\) ist. Dieses Verfahren verwendet wie Quick Sort zwei rekursive Aufrufe zum Sortieren von Teillisten, stellt aber sicher, dass sich dabei die Listen-Größen unabhängig von den Listen-Elementen halbieren, wodurch logarithmische Rekursionstiefe garantiert wird.
Intuitiv können wir das Verfahren wie folgt beschreiben:
-
Teile die Eingabe-Liste in zwei Hälften und sortiere diese rekursiv.
-
Durchlaufe dann die sortierten Hälften und füge sie zu einer Liste zusammen, dass alle Elemente in sortierter Reihenfolge enthält.
Die rekursiven Aufrufe verfahren nach dem selben Prinzip. Für die Eingabe [3,2,1,6,7,4,8,5] ergeben sich also die folgenden Zwischenschritte. Hierbei fassen wir Operationen auf gleicher Rekursionstiefe zusammen. Bei dieser Liste der Größe acht ergeben sich also drei Schritte.
[3,2,1,6,7,4,8,5][2,3,1,6,4,7,5,8][1,2,3,6,4,5,7,8][1,2,3,4,5,6,7,8]
Definieren Sie eine rekursive python-Funktion (keine Prozedur) merge_sort, die das Merge Sort Verfahren implementiert. Die Eingabe-Liste soll von dieser Funktion nicht verändert werden.1 Nach zwei rekursiven Aufrufen sollen die sortierten Hälften zusammengefügt werden. Definieren Sie dazu eine Funktion merge mit zwei Listen als Parametern, die als Ergebnis eine sortierte Liste mit den Elementen beider Parameter zurück liefert.
Untersuchen Sie Ihre Implementierung experimentell. Wie verhalten sich die Laufzeiten in Abhängigkeit von der Eingabegröße?
Bonusaufgabe: Heap-Sort Prozedur implementieren
Von den besprochenen effizienten Sortierverfahren hat Quick Sort den Vorteil, dass keine neue Liste angelegt werden muss und den Nachteil, dass die Laufzeit im schlechtesten Fall quadratisch ist. Andererseits ist es nicht leicht, Merge Sort zu implementieren, ohne eine neue Liste anzulegen. Dafür ist die Laufzeit auch im schlechtesten Fall in \(O(n\cdot log(n))\).
In dieser Aufgabe sollen Sie ein Sortierverfahren implementieren, dass beide Vorteile vereint. Die Idee dazu ist eine Variante von Max Sort, die wir in mehreren Schritten entwickeln.
Max Sort sortiert eine Liste so, dass die Liste zu jeder Zeit aus einem unsortierten (vorderen) und einem sortierten (hinteren) Bereich besteht. Der sortierte Bereich wird dabei schrittweise vergrößert, indem das größte Element des unsortierten Bereiches an die Grenze getauscht wird.
Die Grundidee von Heap Sort ist es, den unsortierten Bereich so zu strukturieren, dass das größte Element des unsortierten Bereichs schneller gefunden werden kann als bei Max Sort. In jedem Schritt wird dabei nur logarithmischer Aufwand nötig sein, das größte Element zu finden und die dazu nötige Struktur aufrecht zu erhalten.
Wenn der unsortierte Bereich sortiert wäre, wäre es einfach, das größte Element zu finden. Den unsortierten Bereich zu sortieren ist ja aber gerade das Ziel eines Sortieralgorithmus - als Zwischenschritt zum Auffinden des größten Elementes wäre es zu aufwändig. Interessanter Weise gibt es eine andere Art, den unsortierten Bereich so zu strukturieren, dass man das größte Element einfach finden kann, und diese Art der Strukturierung ist weniger aufwändig als eine Sortierung.
Heaps
Die Heap-Datenstruktur ordnet enthaltene Einträge in einer Baumstruktur an. Ein Heap mit Zahlen als Einträgen ist entweder eine Zahl (in dem Fall enthält der Heap genau eine Zahl) oder eine Verzweigung, die eine Zahl als Beschriftung enthält und links und rechts davon Heaps als Kindknoten enthalten kann. Wir können die Baumstruktur durch Klammern kenntlich machen. Hier ist ein Beispiel für einen Heap in dieser Schreibweise.
(((2 17 7) 19 3) 100 (25 36 1))
Zeichnen Sie diesen Heap als Baum und betrachten Sie seine Ebenen: Die erste Ebene enthält die Wurzel des Baumes, die zweite Ebene die Beschriftungen der Kindknoten der Wurzel und so weiter.
Zusätzlich müssen Heaps die folgenden Eigenschaften erfüllen:
- Die Beschriftung eines Knotens ist nicht kleiner als die Beschriftungen seiner Kindknoten, sofern welche vorhanden sind.
- Alle Ebenen bis auf die unterste sind vollständig. Nur bei Knoten der beiden untersten Ebenen fehlen also Kindknoten.
- Die unterste Ebene ist von links nach rechts besetzt. Sobald von links nach rechts betrachtet ein Knoten fehlt, folgt kein weiterer Kindknoten der vorletzten Ebene.
Die erste Eigenschaft hat zur Folge, dass das größte Element an der Wurzel des Heaps steht. Die beiden anderen Eigenschaften haben zur Folge, dass der Heap auf eindeutige Weise aus einer Auflistung seiner Einträge in sogenannter Ebenenordnung rekonstruiert werden kann. Eine solche Auflistung der Einträge des oben gezeigten Heaps sieht wie folgt aus.
100 19 36 17 3 25 1 2 7
Der einzige Eintrag der ersten Ebene ist die Beschriftung der Wurzel des Heaps, also 100. Danach folgen die Beschriftungen der Kinder des Wurzelknotens, nämlich 19 und 36. Anschließend werden die Beschriftungen der dritten Ebene, nämlich 17, 3, 25 und 1 von links nach rechts aufgelistet. Die vierte Ebene ist nicht vollständig besetzt und enthält ganz links die beiden Einträge 2 und 7. Wie man sieht, steht der größte Eintrag ganz vorne. Eine umgekehrt sortierte Auflistung der Elemente würde ebenfalls einem Heap entsprechen. Um die Heap-Eigenschaften zu erfüllen ist es aber nicht notwendig, dass die Einträge in Ebenenordnung vollständig sortiert sind.
Die Auflistung der Einträge eines Heaps in Ebenenordnung erlaubt es, einen Heap als Liste darzustellen. Der gezeigte Heap kann dementsprechend wie folgt in python dargestellt werden.
[100,19,36,17,3,25,1,2,7]
Diese Reihenfolge erlaubt es, die Positionen der Listen-Einträge mit der besprochenen Baumstruktur in Beziehung zu setzen. Wenn \(p\) die Position eines inneren Knotens ist, ist \(2p+1\) die Beschriftung seines linken und \(2p+2\) die Beschriftung seines rechten Kindknotens. Zum Beispiel steht die Beschriftung 100 der Wurzel des Heaps an Position 0. An der Position \(2\cdot 0+1 = 1\) steht die 19, die Beschriftung des linken Kindknotens der Wurzel. An Position \(2\cdot0+2 = 2\) steht die 36, also die Beschriftung des rechten Kindes der Wurzel. Das linke Kind der 19 an Position \(1\) ist die 17 an Position \(2\cdot 1+1 = 3\); das rechte Kind der 17 an Position \(3\) ist die 7 an Position \(2\cdot 3+2 = 8\).
Funktionen auf Heaps programmieren
Schreiben Sie python-Funktionen left_child und right_child, die eine Position als Argument erwarten und die Position des linken bzw. rechten Kindknotens zurück liefern. left_child(1) soll also zum Beispiel 3 zurück liefern, und right_child(3) soll 8 zurück liefern.
Um eine unstrukturierte Liste in die Darstellung eines Heaps zu transformieren, müssen die Elemente so umsortiert werden, dass der der Liste entsprechende Heap alle Heap-Eigenschaften erfüllt. Die zweite und dritte Eigenschaft dienten nur der eindeutigen Darstellung als Liste. Aber die Eigenschaft, dass die Beschriftung der Wurzel nicht kleiner ist als die der Kindknoten der Wurzel kann in einer unstrukturierten Liste verletzt sein.
Zunächst beschäftigen wir uns damit, wie wir die Heap-Struktur aufrecht erhalten können, wenn die erste Heap-Eigenschaft nur an der Wurzel verletzt ist. Ein solcher Heap ist hier gezeigt:
((2 19 17) 7 3)
In diesem Heap erfüllen die Kindknoten die erste Heap-Eigenschaft, denn die 19 ist größer als die 2 und die 17, und die 3 hat keine Kindknoten. An der Wurzel ist die Eigenschaft allerdings verletzt, denn die 7 ist kleiner als die 19.
Um den Heap zu reparieren, können wir die Beschriftung 7 der Wurzel mit dem Maximum der Beschriftungen der Kindknoten tauschen. Dadurch ergibt sich der folgende Heap.
((2 7 17) 19 3)
Durch den Tausch ist nun die Heap-Eigenschaft am linken Kindknoten der Wurzel verletzt. Wir können das beschriebene Verfahren rekursiv auf diesen Kindknoten anwenden, um die entstandene Verletzung der Heap-Eigenschaft zu reparieren. Dadurch wird die 7 mit der 17 vertauscht, so dass sich der folgende Heap ergibt.
((2 17 7) 19 3)
Dieser Heap verletzt nun keine Heap-Eigenschaft mehr, da die 7 keine Kindknoten hat.
Definieren Sie eine rekursive Prozedur repair die das beschriebene Verfahren für Heaps in Listen-Darstellung implementiert. Die Prozedur soll drei Argumente erwarten:
- Die Liste, die den dargestellten Heap enthält
- Die Position der Wurzel des Heaps, an der die Heap-Eigenschaft verletzt sein könnte
- Die Größe des Heaps als Obergrenze für gültige Positionen
Der Effekt eines Aufrufs repair(a,root,size) soll sein, dass der Heap nach dem Aufruf die erste Heap-Eigenschaft erfüllt wenn sie vorher höchstens an der Wurzel verletzt war. Die übergebene Position der Wurzel erlaubt es, die Prozedur auch für Kindknoten aufzurufen. Die übergebene Obergrenze erlaubt es, zu testen, ob die Wurzel Kindknoten hat.
Um die definierte Prozedur anwenden zu können, muss sichergestellt sein, dass die erste Heap-Eigenschaft nur an der Wurzel verletzt ist. Wir müssen sie also von unten nach oben (in Listen-Darstellung also von hinten nach vorne) anwenden, um eine komplett unstrukturierte Liste in einen Heap umzuwandeln.
Definieren Sie eine Prozedur make_heap, die eine unstrukturierte Liste in einen Heap umwandelt. Die Prozedur soll als Argument eine unstrukturierte Liste erwarten und als Effekt dieses in einen Heap umwandeln, indem Schrittweise die Prozedur repair aufgerufen wird.
Heap Sort programmieren
Wir können nun mit Hilfe der definierten Prozeduren den Heap Sort Algorithmus implementieren. Dieser wandelt zunächst die übergebene Liste in einen Heap um. Anschließend wird wie bei Max Sort das größte Element des unsortierten Bereichs (das wegen der Heap-Eigenschaft an Position 0 steht) an die Grenze zum sortierten Bereich getauscht, der sich dadurch schrittweise vergrößert. Durch den Tausch kann die Heap-Eigenschaft nun an der Wurzel des Heaps, der den unsortierten Bereich darstellt, verletzt sein, was gegebenefalls vor dem nächsten Schritt des Algorithmus repariert werden muss.
Definieren Sie eine Prozedur heap_sort, die diesen Algorithmus implementiert. Als Argument soll die Prozedur eine unstrukturierte Liste erwarten und als Effekt diese Liste sortieren.
-
Es ist nicht leicht den Merge-Schritt von Merge Sort in place, das heißt durch direkte Manipulation der Eingabe-Liste zu implementieren. Einfacher ist es, eine neue Liste zu erzeugen, die die zusammengefügten Elemente enthält. ↩︎
19.5 Lösungen
Lösungen
Aufgabe: Max Sort implementieren
Zur Implementierung von Max Sort durchlaufen wir das Feld von hinten nach vorne und tauschen dabei jeweils das entsprechende Element mit dem größten seiner Vorgänger. Wir definieren dazu einen Index j in Abhängigkeit von i, der das Feld rückwärts durchläuft.
def max_sort(a):
for i in range(0, len(a)):
j = len(a) - i - 1
swap(a, j, max_pos(a, j))
Ein Aufruf max_pos(a, to) liefert die Position des größten Elementes in a bis zur Position to.
def max_pos(a, to):
pos = 0
for i in range(0, to):
if a[i+1] > a[pos]:
pos = i + 1
return pos
Aufgabe: Insertion Sort experimentell analysieren
Bei den durchgeführten Tests mit sortierten Listen ist insertion_sort deutlich schneller als min_sort:
1000:
0.00014853477478027344
2000:
0.0003032684326171875
4000:
0.0005826950073242188
8000:
0.0012249946594238281
Die wichtigere Beobachtung ist jedoch nicht, dass die Laufzeiten geringer sind, sondern, dass sie langsamer ansteigen: Bei Verdoppelung der Eingabegröße ergibt sich ungefähr die doppelte Laufzeit und nicht mehr wie bei min_sort die vierfache.
Dies gilt jedoch nur für bereits sortierte Listen. Um unsere Tests mit unsortierten Listen zu wiederholen, definieren wir eine Funktion, die umgekehrt sortierte Listen gegebener Größe erzeugt.
def descending(size):
a = [None] * size
for i in range(0, size):
a[i] = size - i
return a
Zum Beispiel liefert der Aufruf descending(5) das Ergebnis [5,4,3,2,1] zurück. Wenn wir diese Funktion zum Erzeugen der Testeingaben verwenden, ergibt sich die folgende Ausgabe:
1000:
0.12551259994506836
2000:
0.49935364723205566
4000:
2.014533519744873
8000:
8.014490604400635
Bei Verdoppelung der Eingabegröße umgekehrt sortierter Listen vervierfacht sich also die Laufzeit von Insertion Sort, wie wir es auch schon bei Selection Sort beobachtet hatten.
Bonusaufgabe: Insertion Sort rekursiv implementieren
Die folgende rekursive Prozedur implementiert den Insertion Sort Algorithmus.
def ins_sort(a, to):
if to > 0:
ins_sort(a, to-1)
insert_backwards(a, to)
Falls to <= 0 gilt, ist das zu sortierende Anfangsstück bereits
sortiert, da es aus höchstens einem Element besteht. Falls to > 0
ist, sortieren wir rekursiv das Anfangsstück bis zur Position to-1
und fügen dann das Element an Position to rückwärts in den
sortierten Bereich ein.
Die rekursive Implementierung führt die selben Vergleiche und Vertauschungen aus wie die vorherige Implementierung mit einer Zählschleife. Die Laufzeiten der beiden Implementierungen sind also ungefähr gleich.
Hausaufgabe: Quick Sort dokumentieren
Zu Beginn wird die Liste
a = [3,2,1,6,7,4,8,5]
mit dem Aufruf partition(a,0,7) partitioniert. Nach diesem Aufruf (der die Position 2 zurückliefert) sind die Elemente von a wie folgt umgeordnet.
a = [1,2,3,6,7,4,8,5]
Nun wird der Bereich von Position 0 bis 1 mit dem Aufruf partition(a,0,1) partitioniert, wobei keine Elemente vertauscht werden. Anschließend folgt der Aufruf partition(a,3,7) des zweiten rekursiven Aufrufs von quick_sort. Er liefert als Ergebnis die Position 5 zurück und ordnet die Elemente in a wie folgt um.
a = [1,2,3,5,4,6,8,7]
Schließlich folgen in weiteren rekursiven Aufrufen von quick_sort die Aufrufe partition(a,3,4) und partition(a,6,7), die nacheinandner dafür sorgen, dass a sortiert wird.
a = [1,2,3,4,5,6,8,7]
a = [1,2,3,4,5,6,7,8]
Aufgabe: Aufgabe: Einfache Prozedur zum Sortieren analysieren
-
Der Rumpf der mutierenden Prozedur
simple_sortenthält zwei geschachtelte Zählschleifen. Die äußere verwendet die Zählvariablei, die innerej. Der innere Schleifenrumpf enthält eine optionale Anweisung deren Bedingung die Elemente an den Indizesiundjvergleicht. Im Rumpf der optionalen Anweisung steht ein Aufruf der Prozedurswap. -
Die folgende Programmtabelle dokumentiert die Ausführung des Aufrufs
simple_sort([2,1,3]).PP i j a[i] < a[j] a 0 [2,1,3] 1 0 2 0 3 False 2 1 3 False 2 2 3 True 4 [3,1,2] 1 1 2 0 3 True 4 [1,3,2] 2 1 3 False 2 2 3 False 1 2 2 0 3 False 2 1 3 True 4 [1,2,3] 2 2 3 False -
Die Prozedur
simple_sortsortiert jede beliebige übergebene Liste von Zahlen. -
Relevant für die Laufzeit ist vor allem die Anzahl durchgeführter Vergleiche. Sie ist eine obere Schranke für die Anzahl der durchgeführten Vertauschungen. Die Laufzeit ist beschrieben durch $O(n^2)$, falls $n$ die Anzahl der Elemente der übergebenen Liste ist.
-
Alle in der Aufgabe genannten Aussagen treffen zu.
Aufgabe: Merge-Sort Funktion implementieren
Die rekursive Funktion merge_sort liefert eine Kopie ihrer Eingabe zurück, wenn diese höchstens ein Element enthält. Wenn nicht, wird die übergebene Liste in zwei Hälften geteilt, die rekursiv sortiert und dann zusammengeführt werden.
def merge_sort(a):
if len(a) <= 1:
return a + [] # return a copy
else:
half = len(a) // 2
return merge(merge_sort(a[0:half]), merge_sort(a[half:len(a)]))
Die Funktion merge fügt zwei sortierte Listen zu einer sortierten Liste zusammen:
def merge(a, b):
c = [None] * (len(a) + len(b))
l = 0
r = 0
# as long as there are elements left
while l + r < len(c):
# we pick the next element from a
if l < len(a) and (r >= len(b) or a[l] <= b[r]):
c[l+r] = a[l]
l = l + 1
else: # or the next element from b
c[l+r] = b[r]
r = r + 1
return c
Sowohl für sortierte als auch für unsortierte Eingaben wird die Laufzeit bei Verdoppelung der Eingabegröße etwas mehr als verdoppelt. Dies legt die (tatsächlich zutreffende) Vermutung nah, dass die Laufzeit in \(O(n\cdot log(n))\) ist.
Bonusaufgabe: Heap-Sort Prozedur implementieren
def swap(a, i, j):
temp = a[i]
a[i] = a[j]
a[j] = temp
def left_child(pos):
return 2*pos + 1
def right_child(pos):
return 2*pos + 2
# restore heap property (node >= child) assuming it for children
def repair(a, root, size):
max = root
left = left_child(root)
if left < size and a[max] < a[left]: # left child exists and is larger
max = left
right = right_child(root)
if right < size and a[max] < a[right]: # right child exists and is larger
max = right
if max != root: # heap property is violated
swap(a, root, max)
repair(a, max, size)
def make_heap(a):
for i in range(0, len(a)):
repair(a, len(a) - i - 1, len(a))
def heap_sort(a):
make_heap(a)
for i in range(0, len(a)-1):
j = len(a) - i - 1
swap(a, 0, j)
repair(a, 0, j)
20. Objekte und ihre Identität
20.1 Mutation
Bei Listen haben wir auch schon gesehen, dass wir den internen Zustand ändern können. Zum Beispiel haben wir factorials[i] = i * factorials[i-1] geschrieben, um in einer Wiederholung mit der Zählvariablen i eine Liste von Fakultäten zu erzeugen. Solche sogenannten Mutationen von Objekten können auch in Prozeduren abstrahiert werden. Ein typisches Beispiel ist die Prozedur swap, die zwei Elemente in einer Liste vertauscht:
def swap(a,i,j):
x = a[i]
a[i] = a[j]
a[j] = x
Der Rumpf der Prozedur swap enthält zwei Mutationen der in dem Parameter a gespeicherten Liste.
Wir können unter Verwendung von swap kompliziertere mutierende Prozeduren definieren; zum Beispiel eine, die die Reihenfolge der Elemente einer Liste umkehrt:
def reverse(a):
for i in range(0,len(a)//2):
swap(a, i, len(a)-i-1)
20.1.1 Aufgaben
Aufgabe: Mutation von Listen beschreiben
Beschreiben Sie umgangssprachlich die Arbeitsweise des folgenden Python-Programms.
m = 0
for i in range(1,len(a)):
if a[i] < a[0]:
m = m + 1
swap(a,i,m)
swap(a,0,m)
Die Prozedur swap sei wie im vorangehenden Kapitel definiert.
Gehen Sie davon aus, dass a eine nicht-leere Liste ist, das Zahlen enthält, und beschreiben Sie, wie sich (für beliebige solche Listen) die Reihenfolge der Elemente von a durch dieses Programm verändert.
Überprüfen Sie Ihre Beschreibung anhand des Beispiels a = [3,1,5,2,4]
und erstellen Sie im Fall von Unklarheiten eine Programmtabelle, die den Programmablauf verdeutlicht.
20.2 Objekt-Identität
Wir wollen in diesem Kapitel das Verhalten von Programmen mit Mutationen genauer verstehen lernen. Dazu betrachten wir zunächst das folgende Programm:
a = [1,2,3]
b = [1,2,3]
reverse(a)
print(b)
Die Ausgabe dieses Programms ist (wie zu erwarten ist) [1,2,3], da zwar die Reihenfolge der Elemente von a umgekehrt, dann aber der Wert von b ausgegeben wird, der nicht verändert wurde.
Durch eine kleine Änderung ändert sich die Ausgabe dieses Programms:
a = [1,2,3]
b = a
reverse(a)
print(b)
In der zweiten Zeile wird jetzt der Variablen b der Wert von a zugewiesen; die anderen Zeilen bleiben unverändert. Durch diese Änderung gibt das Programm nicht mehr [1,2,3] aus sondern [3,2,1], also den Wert der umgekehrten Liste a, obwohl noch immer b ausgegeben wird. Der Grund für dieses Verhalten ist, dass a und b als Werte dieselbe Liste haben und nicht nur wie vorher Listen mit denselben Elementen.
Obwohl also im ersten Programm die a und b zugewiesenen Listen die gleichen Elemente enthalten, handelt es sich bei ihnen um unterschiedliche Objekte mit unterschiedlichen Identitäten. Die Veränderung des Zustands des einen Objektes hat keinen Einfluss auf den Zustand des anderen.
Im zweiten Programm hingegen wird nur ein list-Objekt erzeugt und als Wert den Variablen a und b zugewiesen. Dadurch ändert sich auch der Zustand der in b gespeicherten Liste, sobald der Zustand der in a gespeicherten Liste geändert wird, da es sich dabei um dasselbe Objekt handelt.
Um diesen Effekt besser zu verstehen, können wir Objekte als Kästen zeichnen, in die wir ihren Zustand schreiben und Variablen als Referenzen auf Objekte, die auf entsprechende Kästen zeigen. Für das erste Programm ergeben sich dabei zwei Kästen mit gleichem Zustand, auf die jeweils eine Variable zeigt. Im zweiten Programm ergibt sich nur ein Kasten, auf den zwei Variablen zeigen.
Der Unterschied zwischen identischen Objekten und solchen, deren Zustände lediglich den gleichen Wert haben, kann in Python durch unterschiedliche Vergleichsfunktionen beobachtet werden. Der Vergleichsoperator == vergleicht die Werte von Objekten während das Schlüsselwort is deren Identität vergleicht. Die folgenden Aufrufe demonstrieren diesen Unterschied:
>>> a = [1,2,3]
>>> b = [1,2,3]
>>> c = a
>>> a == b
True
>>> b == c
True
>>> a == c
True
>>> a is b
False
>>> b is c
False
>>> a is c
True
20.3 Weitere Mutations-Anweisungen
Bisher haben wir gesehen, wie wir Listen mutieren können, indem wir einzelne Elemente an einem gegebenen Index überschreiben. Wir können auch Teil-Listen durch andere ersetzen, um mehrere Elemente auf einmal zu überschreiben, einzufügen oder zu entfernen.
List slices haben wir im Kapitel Programmierung mit Listen bereits kennen gelernt, um Teil-Listen zu referenzieren. Mit Slice assignments können wir eine Liste mutieren, die eine Teil-Liste durch eine andere Liste ersetzen:
>>> nums = [1,2,3]
>>> nums[1:3] = [3,5] # slice assignment
>>> nums
[1, 3, 5]
>>> nums[1:1] = [2]
>>> nums
[1, 2, 3, 5]
>>> nums[3:4] = []
>>> nums
[1, 2, 3]
Links vom Gleichheitszeichen steht hierbei ein Ausdruck, der wie die Selektion einer Teil-Liste (List slice mit Start- und End-Index) aussieht. Rechts vom Gleichheitszeichen steht eine Liste, die für die so beschriebenen Elemente eingesetzt wird. Beachtenswert ist, dass die Anzahl der entfernten Elemente und die der eingefügten Elemente nicht gleich sein müssen und dass beide auch Null sein können.
20.3.1 Aufgaben
Aufgabe: Objekte und Referenzen visualisieren
Visualisieren Sie die beim Ablauf der folgenden Programme erzeugten Objekte und Referenzen mit Kästen und Pfeilen und geben Sie jeweils die Ausgabe des Programms an.
Hinweis: Die vordefinierte Methode reverse mutiert Listen genau so
wie die von uns definierte gleichnamige Prozedur.
# 1. Programm
def test(a,b):
a.reverse()
print(a)
print(b)
print(a == b)
return a is b
x = [1,2,3]
print(test(x,x))
print(test(x,[1,2,3]))
# 2. Programm
nums = [1,2,3]
lists = [nums,[1,2,3]]
nums = [4,5,6]
lists[1] = lists[0]
nums = lists[1]
nums[0:3] = [7,8,9]
print(lists[0][0])
Aufgabe: Methoden zur Mutation von Listen
# Testing List methods
>>> li = [42,17,18,39,12,4,42]
>>> li.reverse()
>>> li
Untersuchen Sie im Python-Interpreter ebenso die List-Methoden append(a), clear(), copy(), count(a), extend(a), index(a), insert(n, a), pop(n), remove(a), sort(). Spezifizieren Sie ggf. die Parameter. Geben Sie die Methoden an,
- die die Liste nicht mutieren,
- die einen Wert zurückliefern
Versuchen Sie zunächst, experimentell Effekte und Rückgabewerte der Methoden zu ermitteln, bevor sie Quellen zurate ziehen.
Aufgabe: Objektidentitäten und Mutationen analysieren
Analysieren Sie mithilfe des Python-Interpreters die folgenden Anweisungen:
>>> list1 = [42,17,18,39,12,4,42]
>>> list2 = list1
>>> list3 = list(list1)
>>> list4 = list1+[]
>>> list5 = list1.copy()
>>> list2.sort()
>>> list6 = sorted(list3)
Geben Sie an, welche Listen
- identisch sind (Objektidentität)
- gleich sind (Wertgleichheit)
- sortiert sind
Aufgabe: Mutation von Listen programmieren
Definieren Sie eine Prozedur replace mit drei Parametern a, b, und c, die die Liste a mutiert. In der Liste a sollen dabei alle Vorkommen der Teilliste in b durch die Liste in c ersetzt werden. Verwenden Sie dazu außer slice assignments keine weiteren vordefinierten mutierenden Methoden. Schreiben Sie mit Hilfe der definierten Prozedur ein Programm, das alle Vorkommen der Zahlenfolge 1,2,3 in der Liste [1,2,3,4,1,2,1,2,3,4] durch die Zahl 123 ersetzt und das Ergebnis [123,4,1,2,123,4] ausgibt.
20.4 Mutation als Seiteneffekt
Die Mutation des Zustands von Objekten ist ein Effekt. Effekte werden auch als Seiteneffekt bezeichnet, wenn sie sozusagen nebenbei erfolgen, zum Beispiel zusätzlich zu einem berechneten Ergebnis oder unabsichtlich neben einem weiteren beabsichtigten Effekt.
Betrachten Sie diese rekursive Definition der Funktion rev.
Anders als von der zuvor definierten Prozedur reverse
wird das Argument hier nicht mutiert.
Stattdessen wird eine umgekehrte Liste zurückgeliefert.
Diese Funktion hat keinen Effekt, also auch keinen Seiteneffekt.
def rev(a):
if len(a) > 1:
half = len(a) // 2
# a == left + right
left = a[0:half]
right = a[half:len(a)]
return rev(right) + rev(left)
else:
return a
Der rekursive Fall teilt das Argument in zwei Hälften,
berechnet deren Umkehrung rekursiv
und hängt die Ergebnisse in umgekehrter Reihenfolge aneinander.
Die Implementierung nutzt die folgende Eigenschaft,
die jede reverse-Funktion erfüllen sollte:
reverse(l + r) == reverse(r) + reverse(l)
Ist das Argument kurz genug (seine Länge höchstens 1), so wird die Rekursion abgebrochen. In diesem Fall ist das Argument gleich seiner Umkehrung, so dass es selbst zurückgegeben wird.
Betrachten Sie die folgende Prozedur, die rev verwendet, um aus einer übergebenen Liste eine neue zu berechnen,
in dem die Elemente erst rückwärts und dann vorwärts stehen.
def back_and_forth(a):
result = rev(a)
result[len(a):len(a)] = a
print('Aus ' + str(a) + ' wird ' + str(result))
Bei einem Aufruf dieser Prozedur wird von der enthaltenen Ausgabeanweisung sowohl die als Argument übergebene Liste als auch die neu berechnete Liste ausgegeben:
>>> back_and_forth([1,2,3])
Aus [1,2,3] wird [3,2,1,1,2,3]
Die neu berechnete Liste wird durch Mutation des Ergebnisses von rev erzeugt, indem die ursprüngliche Liste hinten in das umgekehrte eingefügt wird.
Diese Mutation des in der Variablen result gespeicherten Ergebnisses von rev
ist ein weiterer Effekt von back_and_forth,
der zusätzlich zur Ausgabe erfolgt.
Da die Variable result nur im Rumpf der Prozedur back_and_forth sichtbar ist,
könnte man meinen,
dass dieser zusätzliche Effekt lediglich ein Implementierungsdetail
und von außen (außer in der erzeugten Ausgabe) nicht beobachtbar ist.
Allerdings hat die verwendete rev-Funktion eine Eigenschaft,
durch die dieser zusätzliche Effekt ein unbeabsichtigter Seiteneffekt wird,
wie der folgende Aufruf zeigt.
>>> back_and_forth([1])
Aus [1,1] wird [1,1]
Das ist nicht die beabsichtigte Ausgabe. Richtig hätte die Ausgabe lauten sollen: Aus [1] wird [1,1].
Im Rumpf von back_and_forth wird bei der Erzeugung der neu berechneten Liste auch die als Argument übergebene Liste mutiert, weil die Variablen a und result in diesem Fall auf dasselbe Objekt verweisen. Dass rev im Fall eines kurzen Argumentes (Länge höchstens 1) das Argument selbst zurückliefert, führt hier in Verbindung mit der Mutation des Ergebnisses zu einer unerwünschten Mutation des Argumentes. In diesem Fall ist back_and_forth eine ihr Argument mutierende Prozedur, was nicht beabsichtigt war.
Bei der Definition von back_and_forth kann leicht vergessen werden, dass die Funktion rev in einigen Fällen ihr Argument zurück liefert. Besser wäre es, wenn rev auch im Fall kurzer Argumente ein neues Objekt zurück liefern würde,
damit unbeabsichtigte Mutationen wie in unserem Beispiel vermieden werden. Bei der Definition eigener Funktionen sollten Sie deshalb niemals das Argument selbst zurück liefern, es sei denn die Funktion ist als mutierend beschrieben
und die Tatsache, dass das Argument zurück geliefert wird, ergibt sich aus diesem Kontext.
Bei der oben gezeigten rev-Funktion sollten wir dieser Maßgabe entsprechend die Anweisung return a durch return a + [] ersetzen, um ein neues Objekt zu erzeugen, dessen Wert der gleiche ist wie der des Argumentes a.
20.4.1 Aufgaben
Aufgabe: Geteilte Objekte dokumentieren
Betrachten Sie das folgende Python-Programm.
a = [1,2,3]
b = [a,a,a]
for i in range(0,3):
b[i][i] = 1
sum = 0
for i in range(0,9):
sum = sum + b[i//3][i%3]
print(sum)
Zeichnen Sie (in der besprochenen Darstellung mit Kästen und Pfeilen) die Struktur der erzeugten Listen-Objekte am Programmende.
Wie lautet die von diesem Programm erzeugte Ausgabe? Begründen Sie Ihre Antwort.
Aufgabe: Zyklische Strukturen dokumentieren
Betrachten Sie das folgende python-Programm.
a = [42,42]
a[0] = a
print(a[0][0][1])
Was gibt dieses Programm aus?
Skizzieren Sie die erzeugte Objektstruktur in der besprochenen Darstellung mit Kästen und Pfeilen.
Benennen Sie die einzelnen Anweisungen korrekt und beschreiben Sie ihren Effekt.
20.5 Lösungen
Aufgabe: Mutation von Listen beschreiben
Das gezeigte Programm ordnet die Liste a so um, dass es in zwei Teile aufgeteilt ist: der erste Teil enthält alle Zahlen aus a, die kleiner sind als das (ursprünglich) erste Element; der zweite Teil enthält die restlichen Zahlen. Das ursprünglich erste Element trennt dabei nach Ablauf des Programms die beiden Teile. Es steht an Position m.
Hausaufgabe: Objekte und Referenzen visualisieren
Das erste Programm erzeugt die folgende Ausgabe:
[3,2,1]
[3,2,1]
True
True
[1,2,3]
[1,2,3]
True
False
Im ersten Aufruf von test referenzieren sowohl a als auch b das selbe Objekt, das x referenziert. Die Veränderung des Objektes in a wirkt sich also auch auf das (selbe) Objekt in b aus und die Vergleiche sind beide wahr.
Vor dem zweiten Aufruf hat das Objekt in x den Wert [3,2,1], b zeigt auf ein anderes Objekt. Nachdem das Objekt in a verändert wurde, haben beide Objekte den selben Wert aber eine unterschiedliche Identität.
Das zweite Programm gibt die Zahl 7 aus. Sobald die Mutationsanweisung in der sechsten Programmzeile ausgeführt wird,
sind beide Elemente des in der Variablen lists gespeicherten Listen von Listen dasselbe (hier mutierte) Objekt, das nämlich zu diesem Zeitpunkt auch (wieder) in der Variablen nums gespeichert ist.
Aufgabe: Mutation von Listen programmieren
Die Prozedur replace ersetzt Teile einer Liste durch andere Teile.
def replace(a,b,c):
n = len(b)
if n > 0:
i = 0
while i <= len(a)-n:
if a[i:i+n] == b:
a[i:i+n] = c
i = i + len(c)
else:
i = i + 1
Wichtig ist hierbei,
dass die Zählvariable i um die Länge der eingesetzten Liste erhöht wird und jedesmal neu getestet wird, ob sie noch ein gültiger Index in der durchsuchten Liste ist, das ja seine Länge ändert. Außerdem ist es nicht sinnvoll, Teillisten der Länge Null zu ersetzen. Hier ist ein Programm, das die definierte Prozedur testet.
nums = [1,2,3,4,1,2,1,2,3,4]
replace(nums,[1,2,3],[123])
print(nums)
Aufgabe: Geteilte Objekte dokumentieren
Bei Programmende sieht die Objektstruktur wie folgt aus.
Die in der Variablen a gespeicherte Liste [1,2,3] wird zunächst dreimal als Element in einer weiteren Liste b gespeichert. Da alle drei Elemente von b auf das selbe Objekt verweisen, werden durch die in der ersten Zählschleife ausgeführte Mutation alle Elemente von a auf 1 gesetzt. Die zweite Zählschleife berechnet deshalb die Summe aus neun Einsen, so dass am Ende 9 ausgegeben wird.
Aufgabe: Zyklische Strukturen dokumentieren
Das Programm gibt 42 aus.
Die Variable a zeigt nach Ablauf des Programms auf ein List-Objekt. Das erste Element dieser Liste zeigt auf das selbe List-Objekt, das zweite Element zeigt auf die Zahl 42 (siehe Teil b).
Zeile 1 enthält eine Zuweisung. Anschließend hat die Variable a den Wert [42,42]. Zeile 2 enthält eine Listen-Mutation. Anschließend zeigt das erste Element der in a gespeicherten Liste auf diese Liste selbst. Dadurch wird eine zyklische Struktur erzeugt. Zeile 3 ist eine Ausgabe-Anweisung, die das zweite Element 42 der in a gespeicherten Liste ausgibt.
21. Definition von Objekten
21.1 Rationale Zahlen als Objekte
Als Beispiel definieren wir eine Klasse Bruch von Objekten, die
rationale Zahlen darstellen.
class Bruch:
def __init__(self, zaehler, nenner):
self.zaehler = zaehler
self.nenner = nenner
Das Schlüsselwort class leitet die Klassendefinition ein und ist
gefolgt vom Namen der Klasse.
Innerhalb der Klasse definieren wir eine,
Konstruktor genannte, Methode __init__, die bei der Erzeugung
von Objekten der Klasse ausgeführt wird. Die Methode hat hier drei
Parameter self, zaehler und nenner
Der erste Parameter muss bei der Erzeugung nicht angegeben
werden sondern verweist automatisch auf das neu erzeugte Objekt.
Die restlichen Parameter müssen bei der Erzeugung angegeben werden.
In unserem Beispiel speichern wir deren Werte in den Attributvariablen
zaehler und nenner auf die wir mit der Punkt-Schreibweise des Objektes in self zugreifen können.
Attribute speichern den Zustand konstruierter Objekte
und sind überall innerhalb der Klassendefinition (und in Python sogar außerhalb dieser) sichtbar.
Um Objekte der Klasse Bruch zu erzeugen, rufen wir Bruch als Funktion auf und
übergeben die vom Konstruktor erwarteten Argumente für Zähler und
Nenner. Auch diese Funktion nennen wir Konstruktor.
Sie erzeugt eine neue Instanz der zugehörigen Klasse und ruft dann die Methode __init__ auf.
Bisher haben wir Objekte meist ohne Verwendung expliziter Konstruktoren erzeugt. Für Zahlen, Wahrheitswerte, Zeichenketten und Listen bietet Python spezielle Syntax, die es erlaubt, Objekte kompakter zu initialisieren. Zum Beispiel bei Listen können wir allerdings auch explizite Konstruktoren verwenden, wie die folgenden Aufrufe zeigen.
>>> nums = [1,2,3]
>>> nums2 = list(nums)
>>> nums is nums2
False
>>> nums == nums2
True
Man kann von Listen also eine Kopie anlegen, indem man sie bei der Konstruktion eines neuen Objektes als Parameter an den list Konstruktor übergibt.
Doch nun zurück zu der selbst definierten Klasse für Brüche.
>>> Bruch(3,4)
<__main__.Bruch object at 0x7fe84aed0970>
>>> Bruch(8,6)
<__main__.Bruch object at 0x7fe84ae1c310>
Durch Übergabe von Zähler und Nenner an den Konstruktor Bruch wird jeweils ein neues Objekt erzeugt, das entsprechende Werte in den Attributen zaehler und nenner speichert. In Python werden die erzeugten Objekte standardmäßig durch Angabe des Klassennamens und der Speicheradresse angezeigt. Wir können eine alternative Darstellung definieren, indem wir eine Methode __str__ definieren, die von der str-Funktion automatisch verwendet wird.
Dazu fügen wir innerhalb der Klassendefinition folgendes ein.
def __str__(self):
return str(self.zaehler) + "/" + str(self.nenner)
Auch diese Methode hat (wie alle Methoden) einen ersten Parameter (hier self), der beim Aufruf automatisch auf das Objekt verweist, auf dem die Methode aufgerufen wird. Dadurch ist es möglich, in Methoden auf Attributvariablen (und andere Methoden) zuzugreifen.
Wir erzeugen erneut ein Bruch-Objekt und beobachten, wie es nun angezeigt wird.
>>> drei4tel = Bruch(3,4)
>>> drei4tel
<__main__.Bruch object at 0x7f2c8fcea970>
>>> str(drei4tel)
'3/4'
>>> print(drei4tel)
3/4
Wie wir sehen, wandelt auch print das Argument automatisch mit Hilfe der __str__-Methode in einen String um, wenn diese vorhanden ist. Indem wir zusätzlich eine Methode __repr__ definieren, die __str__ aufruft, können wir beeinflussen, wie Bruch-Objekte in der interaktiven Python-Umgebung angezeigt werden.
def __repr__(self):
return self.__str__()
Hier wird beim Aufruf von __str__ der erste Parameter automatisch mit dem Objekt in self initialisiert, auf dem wir die Methode aufrufen.
Nun werden Brüche auch ohne expliziten Aufruf von str oder print in unserer eigenen Darstellung angezeigt.
>>> acht6tel = Bruch(8,6)
>>> acht6tel
8/6
Es wäre schön, wenn Brüche automatisch gekürzt würden. Dazu können wir Zähler und Nenner im Konstruktor durch deren größten gemeinsamen Teiler teilen. Zur Berechnung dessen verwenden wir den Algorithmus von Euklid.
Wir ersetzen also den Konstruktor __init__ wie hier gezeigt und fügen die Methode ggT hinzu.
def __init__(self, zaehler, nenner):
gcd = self.ggT(zaehler, nenner)
self.zaehler = zaehler // gcd
self.nenner = nenner // gcd
def ggT(self, a, b):
while b != 0:
x = b
b = a % x
a = x
return a
Nun werden alle erzeugten Brüche intern gekürzt dargestellt also auch so angezeigt.
>>> Bruch(8,6)
4/3
Als nächstes wollen wir eine Methode zum Multiplizieren von Brüchen definieren. Diese Methode soll das Ergebnis als neues Objekt zurück liefern und die multiplizierten Objekte nicht verändern.
Zur Definition der Multiplikation definieren wir eine Methode mit dem Namen mal. Deren Implementierung erzeugt ein neues Objekt der Klasse Bruch und greift sowohl auf die eigenen Attribute als auch auf diejenigen des übergebenen Argumentes zu.
def mal(self, other):
return Bruch(
self.zaehler * other.zaehler,
self.nenner * other.nenner
)
Nun können wir Brüche wie folgt multiplizieren.
>>> drei4tel = Bruch(3,4)
>>> acht6tel = Bruch(8,6)
>>> drei4tel.mal(acht6tel)
1/1
Wie wir sehen, wird das Ergebnis dabei automatisch gekürzt. Zur Implementierung des kürzenden Konstruktors haben wir eine Methode ggT definiert, die wir auch außerhalb der Klassendefinition auf Bruch-Objekten aufrufen können.
>>> drei4tel.ggT(24,16)
8
Wir hatten nicht beabsichtigt, Brüchen die ggT-Funktion als nach außen sichtbare Methode hinzuzufügen. Wir wollten diese lediglich im Konstruktor verwenden, um Brüche zu kürzen.
In Python können die Namen von Attributen und Methoden mit einem Unterstrich beginnen. Dadurch wird per Konvention signalisiert, dass diese Namen außerhalb der Klassendefinition nicht verwendet werden sollen.1 In anderen Sprachen kann die Sichtbarkeit von Attribute und Methoden gesteuert werden, um die Verwendung außerhalb der Klassendefinition zu verhindern.
Auch auf Attributvariablen können wir in Python von außen zugreifen, wie das folgende Beispiel zeigt.
>>> drei4tel.nenner = 3
>>> drei4tel
3/3
Um unsere Absicht zu kommunizieren, dass Brüche nicht mutierbar sein sollen, können wir die Attributvariablen mit einem Unterstrich am Anfang benennen. Der Zugriff von außen wird dadurch zwar nicht verhindert, aber solche Zugriffe sind zumindest am Unterstrich besser als (per Konvention) unzulässig zu erkennen. Lesender Zugriff von außen sollte jedoch weiterhin erlaubt sein. Dazu definieren wir Methoden, die die Werte von Zaehler und Nenner zurückliefern.
Hier ist noch einmal die komplette Definition der Bruch-Klasse inklusive Verwendung von Unterstrichen um sogenannte private Bestandteile zu kennzeichnen.
class Bruch:
def __init__(self, zaehler, nenner):
gcd = self._ggT(zaehler, nenner)
self._zaehler = zaehler // gcd
self._nenner = nenner // gcd
def _ggT(self, a, b):
while b != 0:
x = b
b = a % x
a = x
return a
def zaehler(self):
return self._zaehler
def nenner(self):
return self._nenner
def mal(self, other):
return Bruch(
self._zaehler * other._zaehler,
self._nenner * other._nenner
)
def __str__(self):
return str(self._zaehler) + "/" + str(self._nenner)
def __repr__(self):
return self.__str__()
-
Bei Verwendung eines doppelten Unterstriches wird in Python eine Umbenennung vorgenommen, die eine Verwendung von außen zwar nicht verhindert, aber versehentliche Verwendung unwahrscheinlicher macht. ↩︎
21.1.1 Übungsaufgaben
Aufgabe: Bruch-Klasse erweitern
Vergegenwärtigen Sie sich die Randfälle der _ggT-Funktion und
probieren Sie aus, wie sich der Konstruktor der Bruch-Klasse
in diesen verhält. Erweitern Sie den Konstruktor gegebenenfalls, um bei
eventuell auftretenden Fehlern eine auf Brüche zugeschnittene
Fehlermeldung auszugeben.
Fügen Sie Methoden zum Addieren, Subtrahieren, Dividieren und Testen auf Gleichheit von Brüchen hinzu. Definieren Sie gegebenenfalls eigene Methoden, die zur Definition der Rechenoperationen hilfreich sind.
Aufgabe: Katzen und andere Tiere
Definieren Sie eine Klasse Animal zur Repräsentation von Tieren. Attribute der Klasse seien species, name, und creation_time.
Definieren Sie die Methoden __init__, __str__ und age, letztere soll das Alter berechnen.
Erzeugen Sie im Hauptprogramm 7 Katzen, die in einer Liste animals gespeichert werden und geben Sie mithilfe von print Name, Alter und Artzugehörigkeit der Tiere aus.
Bonusaufgabe: Klasse für Komplexe Zahlen definieren
Definieren Sie eine Klasse Komplex zur Darstellung Komplexer Zahlen und
implementieren Sie Addition und Subtraktion (wenn Sie möchten auch Multiplikation und Division) als nicht mutierende
Methoden. Implementieren Sie auch __str__- und __repr__-Methoden zur Anzeige
komplexer Zahlen.
21.2 Mutierbare Objekte
Als Beispiel für eine Klasse von Objekten deren Zustand veränderbar ist, implementieren wir Bankkonten, deren Guthaben zum Beispiel durch Einzahlungen verändert werden kann.
Zunächst definieren wir einen Konstruktor zum Erzeugen von Bankkonten. Dieser initialisiert das gespeicherte Guthaben mit dem Wert Null.
class Konto:
def __init__(self):
self._guthaben = 0.0
Obwohl Konten mutierbar sein werden, soll das Guthaben nicht direkt manipuliert werden. Wir benennen das entsprechende Attribut deshalb mit einem Unterstrich und definieren eine lesende Zugriffsmethode. Außerdem definieren wir Methoden zur Darstellung von Konten als Zeichenkette.
def guthaben(self):
return self._guthaben
def __repr__(self):
return str(self)
def __str__(self):
return "Guthaben: " + str(self._guthaben)
Nun definieren wir eine Methode einzahlen, die das gespeicherte
Guthaben um den übergebenen Betrag erhöht.
def einzahlen(self, betrag):
self._guthaben = self._guthaben + betrag
return self
Bei mutierenden Methoden ist es üblich, das Objekt, auf dem die Methode aufgerufen wurde, selbst zurück zu liefern. Dies ermöglicht es, mehrere Veränderungen auf einmal auszuführen, wie die folgenden Aufrufe zeigen.
>>> k = Konto()
>>> k
Guthaben: 0.0
>>> k.einzahlen(100)
Guthaben: 100.0
>>> k.einzahlen(100).einzahlen(100)
Guthaben: 300.0
Analog zum Einzahlen können wir auch das Abheben von einem Bankkonto implementieren.
def abheben(self, betrag):
self._guthaben = self._guthaben - betrag
return self
Mit der bisherigen Implementierung können wir verschiedene Konten anlegen und diese unabhängig voneinander manipulieren. Mit Hilfe einer Überweisung können wir auch Transaktionen zwischen verschiedenen Konten implementieren. Die folgende Methode tut dies.
def ueberweisen(self, other, betrag):
self.abheben(betrag)
other.einzahlen(betrag)
return self
Die folgenden Aufrufe verdeutlichen den Effekt einer Überweisung.
>>> k1 = Konto()
>>> k1.einzahlen(100)
Guthaben: 100.0
>>> k2 = Konto()
>>> k1.ueberweisen(k2, 70)
Guthaben: 30.0
>>> k2
Guthaben: 70.0
21.2.1 Übungsaufgaben
Hausaufgabe: Konto-Klasse erweitern
-
Die definierten mutierenden Methoden der
Konto-Klasse können durch die Angabe negativer Beträge zweckentfremdet werden. Erweitern Sie sie so, dass nur positive Beträge berücksichtigt werden. Passen Sie außerdem die Methode zum Abheben so an, dass nur gedeckte Beträge abgehoben werden können. Damit aufrufender Programmcode überprüfen kann, ob eine Transaktion erfolgreich war, sollen die geänderten Methoden einen entsprechenden Wahrheitswert zurück liefern. -
Fügen Sie eine Methode zum Verzinsen hinzu, die das Guthaben anhand eines festen Zinssatzes erhöht. Der Zinssatz soll bei der Konstruktion eines
Konto-Objektes angegeben werden, wie die folgenden Aufrufe deutlich machen.>>> k = Konto(0.04) Guthaben: 0.0 >>> k.einzahlen(100) >>> k.verzinsen Guthaben: 104.0
Aufgabe: Stack-Klasse implementieren
Definieren Sie eine Klasse Stack zur Implementierung von Sammlungen
nach dem LIFO-Prinzip (last-in, first-out):
Wie auf einem Stapel kann das Element, dass zuletzt eingefügt wurde, als erstes entnommen werden.
Implementieren Sie die folgenden Methoden:
is_emptyliefert einen Wahrheitswert, der angibt, ob der zugehörige Stack leer ist;topliefert, falls der Stack nicht leer ist, das oberste Element des Stacks ohne den Stack zu manipulieren;pushlegt ein übergebenes Element oben auf den Stack;popnimmt ein Element von einem nicht leeren Stack und liefert es zurück.
Definieren Sie außerdem Methoden __init__, __str__ und __repr__, so dass Stacks wie nachfolgend gezeigt in der interaktiven Python-Umgebung verwendet werden können.
>>> s = Stack()
>>> s
Stack:
>>> s.is_empty()
True
>>> s.push(42)
Stack: 42
>>> s.is_empty()
False
>>> s.top()
42
>>> s.push(43)
Stack: 42 43
>>> s.top()
=> 43
>>> s.pop()
43
>>> s
Stack: 42
Aufgabe: Queue-Klasse implementieren
Definieren Sie eine Klasse Queue zur Implementierung von Sammlungen
nach dem FIFO-Prinzip (first-in, first-out):
Wie in einer Warteschlange kann das Element, das als erstes eingefügt wurde, als erstes entnommen werden.
Implementieren Sie die folgenden Methoden:
is_emptyliefert einen Wahrheitswert zurück, der angibt, ob die Queue leer ist;firstliefert das erste Element einer nicht leeren Warteschlange, ohne sie zu manipulieren;enqueuefügt der Warteschlange hinten ein übergebenes Element hinzu;dequeueentfernt das vorderste Element und gibt es zurück.
Definieren Sie darüber hinaus Methoden, __init__, __str__ und __repr__, so dass Queues wie nachfolgend gezeigt in der interaktiven Python-Umgebung verwendet werden können.
>>> q = Queue()
>>> q
Queue:
>>> q.is_empty()
True
>>> q.enqueue(42)
Queue: 42
>>> q.is_empty()
False
>>> q.first()
42
>>> q.enqueue(43)
Queue: 42 43
>>> q.first
42
>>> q.dequeue()
42
>>> q.first()
43
21.3 Lösungen
Lösungen
Aufgabe: Bruch-Klasse erweitern
Hier ist eine neue Version des Konstruktors. Er gibt eine Fehlermeldung aus, wenn ein Bruch konstruiert wird, dessen Nenner Null ist.
def __init__(self, zaehler, nenner):
self._zaehler = zaehler
self._nenner = nenner
if nenner == 0:
print("Der Nenner ist Null!")
return
gcd = self._ggT(zaehler, nenner)
self._zaehler = zaehler // gcd
self._nenner = nenner // gcd
Der folgende Aufruf demonstriert den Effekt dieser Änderung.
>>> Bruch(7,0)
Der Nenner ist Null!
7/0
Hier sind Definitionen der verbleibenden Grundrechenarten inklusive dazu verwendeter Hilfsmethoden.
def negativ(self):
return Bruch(-self._zaehler, self._nenner)
def minus(self, other):
return self.plus(other.negativ())
def kehrwert(self):
return Bruch(self._nenner, self._zaehler)
def durch(self, other):
return self.mal(other.kehrwert())
Zur Definition der Subtraktion definieren wir eine Negationsmethode negativ. Zur Definition der Division definieren wir eine Methode kehrwert. Beide Methoden sind unabhängig von unserer Verwendung nützlich, weshalb wir ihren Namen keinen Unterstrich voranstellen.
Da Brüche gekürzt dargestellt werden, können wir die Vergleichsmethode wie folgt definieren.
def ist_gleich(self, other):
return self._zaehler == other._zaehler and self._nenner == other._nenner
Bonusaufgabe: Klasse für Komplexe Zahlen definieren
Als Namen für die Klasse komplexer Zahlen wählen wir Komplex.
class Komplex
Wir definieren einen Konstruktor, der Real- und Imaginärteil als Parameter erwartet und als entsprechende (private) Attribute speichert.
def __init__(self, real, imag):
self._real = real
self._imag = imag
Für diese Attribute definieren wir lesende Zugriffsmethoden.
def real(self):
return self._real
def imag(self):
return self._imag
Als Zeichenketten-Darstellung für komplexe Zahlen wählen wir die Form a+bi mit Vereinfachungen für einige Sonderfälle. Zum Beispiel Stellen wir die Zahl 1+0i als 1 dar, die Zahl 0-i als -i und so weiter.
def __repr__(self):
return str(self)
def __str__(self):
if self._imag == 0:
return str(self._real)
if self._real == 0:
return self._imag_str()
if self._imag < 0:
return str(self._real) + self._imag_str()
return str(self._real) + "+" + self._imag_str()
Die Hilfsmethode _imag_str gibt die Zeichenkettendarstellung des Imaginärteils zurück und soll nicht von außen verwendet werden.
def _imag_str(self):
if self._imag == 1:
return "i"
if self._imag == -1:
return "-i"
return str(self._imag) + "i"
Wir können nun die Zahl i wie folgt erzeugen und anzeigen lassen.
>>> Komplex.new(0,1)
i
Zur Addition zweier komplexer Zahlen addieren wir deren Real- und Imaginärteile getrennt voneinander. Ist das Argument keine komplexe Zahl interpretieren wir es als reele Zahl und erzeugen eine entsprechende komplexe Zahl vor der Addition.
def plus(self, other):
if type(other) == Komplex:
return Komplex(
self._real + other._real,
self._imag + other._imag
)
else:
return self.plus(Komplex(other, 0))
Durch diesen Trick ist es möglich, komplexe Zahlen mit reellen zu addieren - zumindest, wenn das erste Argument eine komplexe Zahl ist:
>>> i = Komplex.new(0,1)
>>> i.plus(1)
1+i
Zur Subtraktion komplexer Zahlen definieren wir zunächst die Negation und verwenden dann die Addition zum Subtrahieren.
def negativ(self):
return Komplex(-self._real, -self._imag)
def minus(self, other):
if type(other) == Komplex:
return self.plus(other.negativ())
else:
return self.plus(Komplex(-other, 0))
Multiplikation und Division implementieren wir auf Basis von Absolutbetrag und Winkel im Bogenmaß (Radiant), die mit Hilfe vordefinierter mathematischer Funktionen aus Real- und Imaginärteil berechnet werden können, die wir mit import math importieren.
def abs(self):
return math.sqrt(self._real ** 2 + self._imag ** 2)
def rad(self):
return math.atan2(self._imag, self._real)
Zur Multiplikation unterscheiden wir wieder ob das Argument eine komplexe Zahl ist. Falls nicht, interpretieren wir das Argument als reele Zahl und multiplizieren Real- und Imaginärteil getrennt voneinander mit dieser. Ansonsten berechnen wir das Ergebnis in Polarkoordinaten und erzeugen aus diesen das Ergebnis.
def mal(self, other):
if type(other) == Komplex:
return polar(self.abs() * other.abs(), self.rad() + other.rad())
else:
return Komplex(self._real * other, self._imag * other)
Zur Division verfahren wir analog und die Definition der Klasse Komplex ist beendet.
def durch(self, other):
if type(other) == Komplex:
return polar(self.abs() / other.abs(), self.rad() - other.rad())
else:
return Komplex(self._real / other, self._imag / other)
Die hier verwendete Funktion polar zur Konstruktion einer komplexen Zahl aus Polarkoordinaten definieren wir (außerhalb der Klassendefinition) wie folgt.
def polar(abs, rad):
return Komplex(math.cos(rad), math.sin(rad)).mal(abs)
Hierbei wird wieder die Multiplikation auf komplexen Zahlen verwendet, um mit dem Absolutbetrag zu multiplizieren. Unsere Multiplikations-Methode und die polar-Funktion rufen sich also gegenseitig auf, allerdings nicht endlos, da der Absolutbetrag eine reelle Zahl ist.
Hier sind einige Beispielaufrufe zum Testen der Implementierung.
>>> i = Komplex(0,1)
>>> i.mal(i)
-1.0+1.2246467991473532e-16i
>>> i.durch(i)
1.0
>>> i.plus(1).mal(i.minus(1)).durch(2)
-1.0000000000000002+1.2246467991473535e-16i
>>> i.plus(2).mal(i.plus(3))
5.000000000000001+5.0i
>>> i.plus(2).durch(i.plus(3))
0.7+0.09999999999999999i
Hausaufgabe: Konto-Klasse erweitern
Die Methode zum Einzahlen erweitern wir wie folgt, um die Einzahlung negativer Beträge zu verhindern.
def einzahlen(self, betrag):
if 0 <= betrag:
self._guthaben = self._guthaben + betrag
return True
else:
return False
Wir geben statt self nun einen Wahrheitswert zurück, an dem aufrufender Programmcode erkennen kann, ob die Einzahlung erfolgreich war.
Beim Abheben testen wir zusätzlich, ob der auszuzahlende Betrag vom Guthaben gedeckt ist und geben wieder einen Wahrheitswert zurück.
def abheben(self, betrag):
if 0 <= betrag and betrag <= self._guthaben:
self._guthaben = self._guthaben - betrag
return True
else:
return False
Da Ein- und Auszahlungen jetzt fehlschlagen können, müssen wir die Überweisungs-Methode so anpassen, dass sie eine Einzahlung nur genau dann vornimmt, wenn auch die Auszahlung erfolgreich war. Dazu testen wir, ob die Auszahlung erfolgreich war, bevor wir die Einzahlung veranlassen.
def ueberweisen(self, other, betrag):
if self.abheben(betrag):
return other.einzahlen(betrag)
else:
return False
Die Einzahlung ist hier immer erfolgreich, da sie nur bei negativem Betrag fehl schlägt. In diesem Fall wäre aber schon die Auszahlung fehlgeschlagen und die Einzahlung garnicht veranlasst worden.
Um Verzinsung zu implementieren fügen wir dem Konstruktor ein Argument für den Zinssatz hinzu, der in einem Attribut gespeichert wird.
def __init__(self, zinssatz):
self._guthaben = 0.0
self._zinssatz = zinssatz
Auf dieses Attribut können wir nun in der Methode zum Verzinsen zugreifen.
def verzinsen(self):
self._guthaben = self._guthaben * (1 + self._zinssatz)
return self
Aufgabe: Stack-Klasse implementieren
class Stack:
def __init__(self):
self._elems = []
def is_empty(self):
return len(self._elems) == 0
def top(self):
return self._elems[len(self._elems)-1]
def push(self, elem):
self._elems.append(elem)
return self
def pop(self):
return self._elems.pop()
def __repr__(self):
return str(self)
def __str__(self):
result = "Stack:"
for i in range(0, len(self._elems)):
result = result + " " + str(self._elems[i])
return result
Aufgabe: Queue-Klasse implementieren
class Queue:
def __init__(self):
self._elems = []
def is_empty(self):
return len(self._elems) == 0
def first(self):
return self._elems[0]
def enqueue(self, elem):
self._elems.append(elem)
return self
def dequeue(self):
self._elems.pop(0)
return self
def __repr__(self):
return str(self)
def __str__(self):
result = "Queue:"
for i in range(0, len(self._elems)):
result = result + " " + str(self._elems[i])
return result
22. Hierarchische Modularisierung
22.1 Aggregation
Als Aggregation wird das Zusammenfassen
mehrerer Objekte zu neuen bezeichnet. Wir haben bereits ein Beispiel dafür
gesehen: Die Bruch-Klasse fasst einen Zähler und einen Nenner zu einem neuen
Wert zusammen. Die Bestandteile sind ihrerseits jeweils als Zahl-Objekte
representiert. In ähnlicher Weise könnten wir mehrere Zahlen zu Punkten in einem
Koordinatensystem zusammen fassen, mehrere Punkte zu geometrischen Figuren und
mehrere geometrische Figuren zu Bildern. Auf diese Weise entstehen immer
komplexere, hierarchische Daten auf Basis von einfacheren.
Wir wollen im folgenden den bereits verwendeten Mechanismus der Aggregation vertiefen und dann darauf aufbauend das neue Konzept der Vererbung kennenlernen.
Dazu definieren wir eine
Klasse Point zur Darstellung von Punkten in einem
Koordinatensystem.
class Point:
def __init__(self, x, y):
self._x = x
self._y = y
Die Methode __init__ konstruiert einen Punkt aus einer x- und
einer y-Koordinate, indem entsprechende Parameter x und y in
Instanzvariablen _x und _y (auch Attributvariablen genannt) abgespeichert werden.
Durch die Benennung mit einem Unterstrich signalisieren wir,
dass außerhalb der Klassendefinition kein Zugriff
auf die Instanzvariablen erfolgen soll.
Um von außen lesenden Zugriff auf die Koordinaten zu erlauben,
definieren wir innerhalb der Klasse Point Methoden x und y, die
die Werte der entsprechenden Koordinaten zurück liefern.
def x(self):
return self._x
def y(self):
return self._y
Um auch schreibenden Zugriff zu erlauben, definieren wir
(mutierende!) Methoden set_x und set_y, die die Koordinaten auf
übergebene Werte setzen.1
def set_x(self, x):
self._x = x
def set_y(self, y):
self._y = y
Dass der Zugriff auf Attribute, die in Klassen für Objekte definiert sind, nur über bereitgestellte Methoden erfolgt, ist ein Ausdruck von Datenkapselung. Ein Vorteil der Datenkapselung ist es, dass wir den Zugriff einschränken können. Zum Beispiel können wir testen, ob die übergebene Koordinate eine ganze Zahl ist, und nur in disem Fall den aktuellen Wert überschreiben. Dazu verändern wir die Methoden zum Setzen der Koordinaten wie folgt.
def set_x(self, x):
if type(x) == int:
self._x = x
def set_y(self, y):
if type(y) == int:
self._y = y
Eine solche Überprüfung erscheint auch bei der Konstruktion von Punkten sinnvoll. Dazu können wir die gerade definierten Methoden im Konstruktor verwenden, dessen Implementierung wir also wie folgt verändern.
def __init__(self, x, y):
self.set_x(x)
self.set_y(y)
Als nächstes definieren wir eine Klasse Shape zur Darstellung geometrischer
Figuren, die als Zustand einen Punkt kapselt, der angibt, wo die Figur
gezeichnet werden soll.
class Shape:
def __init__(self, point):
self.set_location(point)
def location(self):
return self._location
def set_location(self, point):
if type(point) == Point:
self._location = point
Auch hier definieren wir Methoden zum lesenden und schreibenden
Zugriff auf den internen Zustand der Shape-Objekte. Wir werden
später noch weitere Methoden für Shape-Objekte definieren. Zunächst
jedoch definieren wir spezielle geometrische Figuren als sogenannte
Unterklassen der Klasse Shape.
-
Diese Art Zugriffsmethoden zu definieren ist in Python unüblich. Eine Diskussion von Property-Decorators würde uns aber vom Wesentlichen ablenken. ↩︎
22.2 Vererbung
Zur Definition konkreter geometrischer Figuren verwenden wir eine andere Art der hierarchischen Modularisierung,
nämlich Vererbung.
Vererbung erlaubt es Gemeinsamkeiten unterschiedlicher Klassen in
Oberklassen zusammenzufassen und dann in Unterklassen auf diese
zurückzugreifen. Zum Beispiel haben alle geometrischen Figuren, die
wir definieren werden, einen Punkt, an dem sie gezeichnet werden
sollen, gemeinsam. Alle Klassen zur Darstellung geometrischer Figuren
erben deshalb die entsprechenden Methoden (und den zugehörigen
Zustand) von der Klasse Shape.
Als Beispiel definieren wir die Klasse Circle als Unterklasse der
Klasse Shape.
class Circle(Shape):
def __init__(self, center, radius):
super().__init__(center)
self.set_radius(radius)
def radius(self):
return self._radius
def set_radius(self, radius):
if type(radius) == int:
self._radius = radius
def center(self):
return self.location()
def set_center(self, point):
self.set_location(point)
Die Klassendefinition von Circle hat hier
einen Parameter Shape in runden Klammern, wodurch festgelegt wird, dass
Circle eine Unterklasse von Shape ist.
Der Methode __init__ der Klasse Circle müssen der
Kreismittelpunkt und der Radius übergeben werden. Der Mittelpunkt wird
mit Hilfe des Aufrufs super().__init__(center) an die __init__-Methode der
Oberklasse Shape übergeben, welche diesen im Attribut _location
speichert. Der Radius wird mit Hilfe der Methode set_radius im Attribut
_radius gespeichert.
Die Definition der Methode __init__ überschreibt die Definition
der gleichnamigen Methode der Klasse Shape. Beim Aufruf von
__init__ auf einem Circle-Objekt wird also die neue
Implementierung verwendet statt der alten. Die alte Implementierung
kann mit Hilfe von super() aufgerufen werden,
wie das obige Beispiel zeigt.
Circle-Objekte verfügen über alle Methoden von Shape-Objekten,
wie die Methoden center und set_center zum Zugriff auf den
im Attribut _location der Oberklasse gespeicherten Mittelpunkt zeigen.
In der Regel wird Vererbung verwendet, um hierarchische Zusammenhänge
der definierten Klassen auszudrücken. Zum Beispiel ist jeder Kreis
(Circle) eine Figur (Shape) und jede Instanz der Klasse Circle
ist (indirekt) auch eine Instanz der Klasse Shape. Solche
Zusammenhänge leiten die Definition komplexerer Klassenhierarchien. Da
jede Klasse nur eine Oberklasse aber mehrere Unterklassen hat1,
ergibt sich dadurch eine Baumstruktur. Klassen ohne explizite
Oberklasse erben von der vordefinierten Klasse object, die also die
Wurzel der Baumstruktur aller definierten Klassen ist.
-
Tatsächlich kann eine Klasse in Python auch mehrere Oberklassen haben. In den meisten anderen Objekt-orientierten Sprachen ist das aber nicht erlaubt. ↩︎
22.2.1 Übungsaufgaben
Aufgabe: Klassenhierarchie geometrischer Figuren erweitern
Definieren Sie weitere Klassen zur Darstellung geometrischer Figuren
als Unterklassen der Klasse Shape mit geeignetem Zustand sowie
lesenden und schreibenden Zugriffsmethoden. Definieren Sie mindestens
Klassen Rect und Square zur Darstellung von Rechtecken und
Quadraten und eventuell auch von Ellipsen (Ellipse) und
Parallelogrammen (Parallelogram).
Die Orientierung der geometrischen Figuren soll nur orthogonal zu den Koordinatenachsen erfolgen. gegenüber den Achsen gedrehte Objekte sind nicht gefordert.
Entwerfen Sie zunächst ein Klassendiagramm (Modellierung) bevor Sie die Klassen in Python implementieren und testen.
Überlegen Sie jeweils, wo Sie die Klassen in der Hierarchie einsortieren. Verändern Sie gegebenenfalls auch die Definition bereits definierter Klassen, um die Hierarchie geeignet anzupassen.
22.3 Dynamische und späte Bindung
Mit dem Begriff Bindung bezeichnet man die Auswahl der Implementierung einer Methode zu einem gegebenen Namen. Da Unterklassen Methoden überschreiben können, ist nicht immer ohne weiteres klar, welche Implementierung anzuwenden ist, wie die folgende Diskussion zeigt.
Um die Bindung von Methoden zu verdeutlichen, definieren wir
für jede Unterklasse von Shape eine Methode __repr__ zur Darstellung der
entsprechenden Figur als Zeichenkette.
Da jede Klasse eine __repr__-Methode der Klasse object erbt,
überschreiben wir die geerbte Implementierung mit einer eigenen.
Wir beginnen mit einer __repr__-Methode für die Shape-Klasse.
# in class Shape
def __repr__(self):
return "Shape location=" + str(self._location)
Damit die im Attribut _location gespeicherte Point-Instanz
in eine sinnvolle Zeichenkette umgewandelt wird, überschreiben wir
die __str__-Methode in der Point-Klasse.
# in class Point
def __str__(self):
return "(" + str(self._x) + "," + str(self._y) + ")"
Die drei folgenden Anweisungen erzeugen einen Kreis und ein Rechteck. Anschließend können wir uns in der interaktiven Python-Umgebung deren Darstellung anzeigen lassen.
>>> p = Point(100, 100)
>>> c = Circle(p, 50)
>>> r = Rect(p, 150, 100)
>>> c
Shape location=(100,100)
>>> r
Shape location=(100,100)
Wenn die Rect-Klasse Zugriff auf die linke obere Ecke mit top_left
sowie auf Breite und Höhe mit
Methoden width und height erlaubt, können wir die Methode __repr__
in der Klasse Rect wie folgt überschreiben.
# in class Rect
def __repr__(self):
return (
"Rect top_left=" + str(self.top_left()) +
" width=" + str(self.width()) +
" height=" + str(self.height())
)
Analog dazu können wir die Methode __repr__ in Circle definieren,
indem wir die gespeicherten Attributwerte zusammenfassen.
# in class Circle
def __repr__(self):
return (
"Circle center=" + str(self.center()) +
" radius=" + str(self.radius())
)
Wenn wir nun die oben gemachten Eingaben wiederholen, werden diese
beiden unterschiedlichen Implementierungen der __repr__-Methode
aufgerufen, je nachdem, auf welchem Objekt __repr__ aufgerufen
wird. Dies geschieht selbst dann, wenn wir die Aufrufe in einer
Schleife zusammenfassen.
>>> p = Point(100, 100)
>>> c = Circle(p, 50)
>>> r = Rect(p, 150, 100)
>>> shapes = [c, r]
>>> for i in range(0, len(shapes)):
... print(repr(shapes[i]))
...
Circle center=(100,100) radius=50
Rect top_left=(100,100) width=150 height=100
Obwohl hier textuell nur ein einziger repr-Aufruf steht, werden in
unterschiedlichen Schleifendurchläufen unterschiedliche
Implementierungen der __repr__-Methode verwendet, je nachdem zu welcher Klasse das Element shapes[i] aus der durchlaufenen Liste gehört. Da hier erst zur Laufzeit feststeht, welche Implementierung verwendet wird, spricht man von dynamischer Bindung.
Eine Variante der dynamischen Bindung ist die sogenannte späte Bindung, die wir auch mit Hilfe der __repr__-Methode illustrieren. Dazu fügen wir der Klasse Shape eine Methode __str__ hinzu, die das erste von __repr__ gelieferte Wort zurück liefert.
# in class Shape
def __str__(self):
return repr(self).split()[0]
Der Aufruf von repr verwendet hier die
Implementierung derjenigen Unterklasse von Shape, auf der
__str__ aufgerufen wurde, selbst wenn diese bei der Definition
von __str__ gar nicht bekannt ist.
Da die Rect-Klasse die in Shape definierte Methode __str__
erbt, können wir sie auf dem Rechteck r aufrufen um seine Beschreibung
zu generieren.
>>> p = Point(100, 100)
>>> r = Rect(p, 150, 100)
>>> print(r)
Rect
Ein Aufruf von print ruft indirekt __str__ auf.
22.4 Ersetzbarkeitsprinzip
In der Regel wird die Klassenhierarchie
einer intuitiven Hierarchie der beteiligten Objekte nachempfunden.
So kann man zum Beispiel Square als Unterklasse von Rect
definieren, da jedes Quadrat auch ein Rechteck ist.
Diese Idee kann man weiterführen und fordern, dass überall, wo ein
Rect-Objekt verwendet wird auch ein Square-Objekt verwendet werden
können sollte, ohne dass sich dadurch das Verhalten des Programms
verändert. Intuitiv ist diese (Ersetzbarkeitsprinzip genannte) Forderung
gerechtfertigt, wenn Quadrate sich immer wie Rechtecke verhalten. Da
die Square-Klasse jedoch Rect-Methoden überschreiben kann, ist
dies nicht automatisch gewährleistet, wie das folgende Beispiel zeigt.
Die Rect-Klasse bietet eine mutierende Zugriffsmethode set_width zum
setzen der Breite eines Rechteck-Objektes. Es ist nicht sinnvoll,
diese Methode in der Square-Klasse zu erben, da bei Veränderung der
Breite (ohne gleichzeitiger Veränderung der Höhe) ein Square-Objekt
kein Quadrat mehr darstellen würde. Die Square-Klasse sollte also
die set_width-Methode so überschreiben, dass gleichzeitig auch die Höhe
verändert wird und zwar so, dass die entstehende Figur ein Quadrat
bleibt.
Durch diese Verhaltensänderung in der Unterklasse wird jedoch das genannte
Ersetzbarkeitsprinzip verletzt, da sich nun Square-Objekte anders
verhalten als Rect-Objekte, wenn auf ihnen die set_width-Methode
aufgerufen wird.
>>> p = Point(100, 100)
>>> r = Rect(p, 150, 150)
>>> s = Square(p, 150)
>>> r.set_width(100)
>>> r.height()
150
>>> s.set_width(100)
>>> s.height()
100
Im Allgemeinen kann jedes Überschreiben einer Methode potentiell zu einer Verletzung des Ersetzbarkeitsprinzips führen. Nur wenn die neue Implementierung das Verhalten der alten nicht ändert (und zum Beispiel lediglich effizienter implementiert), bleibt das Ersetzbarkeitsprinzip in Gegenwart von überschriebenen Methoden gewahrt.
22.4.1 Übungsaufgaben
Hausaufgabe: Klassen für arithmetische Ausdrücke definieren
In dieser Aufgabe sollen Sie eine Klassenhierarchie zur Darstellung von arithmetischen Ausdrücken entwerfen.
Entwerfen Sie zunächst ein Klassendiagramm (Modellierung) bevor Sie die Klassen in Python implementieren und testen.
Gemeinsame Oberklasse all Ihrer Klassen soll die folgende Klasse Expression sein:
class Expression:
def __repr__(self):
return str(self)
Die Methode __repr__ gibt die Zeichenkette zurück, die bei der Eingabe von Objekten in python3 angezeigt wird. Die gezeigte Implementierung ruft zur Berechnung dieser Zeichenkette (indirekt) die Methode __str__ auf und gibt das Ergebnis zurück. Welche Implementierung von __str__ wird zur Auswertung dieses Aufrufs verwendet?
Definieren Sie eine Klasse Number zur Darstellung von Zahlen. Objekte dieser Klasse sollen zum Beispiel durch einen Aufruf wie Number(42) erzeugt werden können. Überschreiben Sie in der Klassendefinition die Methode __str__ derart, dass eine textuelle Darstellung der dargestellten Zahl zurückgegeben wird. Ist es sinnvoll, die Klasse Number als Unterklasse von Expression zu definieren? Begründen Sie Ihre Antwort. Fügen Sie der Klasse Number außerdem eine Methode value hinzu, die den Wert der dargestellten Zahl zurückliefert.
Definieren Sie Klassen Sum und Product zur Darstellung von Summen und Produkten arithmetischer Ausdrücke. Objekte dieser Klassen sollen, wie Objekte der Klasse Number, über Methoden __str__ und value verfügen. Implementieren Sie diese beiden Methoden so, dass die folgenden Aufrufe in python3 sich wie gezeigt verhalten:
>>> a = Number(17)
>>> a
17
>>> b = Number(4)
>>> b
4
>>> c = Sum(a,b)
>>> c
(17+4)
>>> d = Product(Number(2), c)
>>> d
(2*(17+4))
>>> d.value()
42
Überlegen Sie, von welcher Klasse Sum und Product erben sollten, um Duplizierung von Quelltext weitgehend zu vermeiden. Gegebenenfalls können Sie auch weitere Klassen definieren. Begründen Sie für jede weitere Klasse, warum Sie ihre Definition für sinnvoll halten.
Hausaufgabe: Klassen für Schachfiguren definieren
In dieser Aufgabe sollen Sie eine Klassenhierarchie zur Repräsentation von Schachfiguren entwerfen. Gemeinsame Oberklasse all Ihrer Klassen soll die folgende Klasse Piece sein:
class Piece:
def __init__(self, color, field):
self._color=color
self.set_position(field)
def position(self):
return self._position
def set_position(self, field):
self._position = field
def move(self, field):
if self.is_allowed(field):
self.set_position(field)
def __repr__(self):
return str(self)
Der Konstruktor wird mit Farbe und Position als Argumente aufgerufen (z.B. “white”, “a1”).
Erläutern Sie die Methoden position, set_position und move.
Die Methode __repr__ gibt die Zeichenkette zurück, die bei der Eingabe von Objekten in python3 angezeigt wird. Die gezeigte Implementierung ruft zur Berechnung dieser Zeichenkette (indirekt) die Methode __str__ auf und gibt das Ergebnis zurück.
Definieren Sie eine Klasse Rook zur Repräsentation von Türmen.
Objekte dieser Klasse sollen zum Beispiel durch einen Aufruf wie Rook("white", "a1") erzeugt werden können.
Überschreiben Sie in der Klassendefinition die Methode __str__ derart, dass eine textuelle Darstellung des Turm-Objektes zurückgegeben wird.
Begründen Sie die Zweckmäßigkeit, die Klasse Rook als Unterklasse von Piece zu definieren.
Fügen Sie der Klasse Rook eine boolesche Methode is_allowed hinzu, die ermittelt, ob der Zug auf ein Feld nach den Schachregeln zulässig ist.
Definieren Sie entsprechend Klassen Bishop und Queen zur Repräsentation von Läufern und Damen.
Objekte dieser Klassen sollen, wie Objekte der Klasse Rook, über Methoden __str__ und is_allowed verfügen. Implementieren Sie diese beiden Methoden so, dass die folgenden Aufrufe in python3 sich wie gezeigt verhalten:
>>> r = Rook("white", "a1")
>>> r
Rook (white) at: a1
>>> r.move("a3") #valid Move
>>> r
Rook (white) at: a3
>>> r.move("b2") #invalid Move
Rook (white) at: a3
>>> b = Bishop("black","c3")
>>> b
Bishop (black) at: c3
>>> b.move("h8")
>>> b
Bishop (black) at: h8
Analysieren Sie, welche Implementierung von __str__ zur Auswertung des Aufrufs Piece#repr verwendet wird.
Untersuchen Sie die Methoden is_allowed der Klassen Rook, Bishop und Queen auf Redundanz und abstrahieren Sie so, dass Duplizierung von Quelltext weitgehend vermieden wird.
22.5 Lösungen
Aufgabe: Klassenhierarchie geometrischer Figuren erweitern
Zur Darstellung von Rechtecken definieren wir eine Klasse Rect als Unterklasse von Shape.
class Rect(Shape):
def __init__(self, top_left, width, height):
super().__init__(top_left)
self.set_width(width)
self.set_height(height)
def width(self):
return self._width
def height(self):
return self._height
def set_width(self, width):
if type(width) == int:
self._width = width
def set_height(self, height):
if type(height) == int:
self._height = height
def top_left(self):
return self.location()
def set_top_left(self, top_left):
self.set_location(top_left)
Das geerbte Attribut _location interpretieren wir hier als obere linke Ecke und speichern zusätzlich Breite und Höhe in Attributen _width und _height. Wir können also mit unserer Implementierung nur achsenparallele Rechtecke darstellen. Zusätzliche zu den Zugriffsmethoden für die neuen Attribute definieren wir Methoden top_left und set_top_left zum Zugriff auf das geerbte _location-Attribut.
Da Quadrate besondere Rechtecke sind, definieren wir eine Klasse Square als Unterklasse der eben definierten Klasse Rect.
class Square(Rect):
def __init__(self, top_left, size):
super().__init__(top_left, size, size)
def size(self):
return self.width()
def set_size(self, size):
if type(size) == int:
self._width = size
self._height = size
def set_width(self, width):
self.set_size(width)
def set_height(self, height):
self.set_size(height)
Die __init__-Methode implementieren wir durch Rückgriff auf die entsprechende Methode der Oberklasse, wobei wir als Breite und Höhe jeweils die übergebene Kantenlänge übergeben. Zum Zugriff auf die Kantenlänge greifen wir auf die gerbten Attribute _width und _height zu, wobei wir sicherstellen, dass Breite und Höhe immer den gleichen Wert haben. Dazu überschreiben wir die schreibenden Zugriffsmethoden set_width und set_height unter Rückgriff auf die neu definierte Methode set_size.
Hausaufgabe: Klassen für arithmetische Ausdrücke definieren
Welche Implementierung von __str__ in der gezeigten Definition von __repr__ aufgerufen wird, hängt davon ab, auf welchem Objekt __repr__ aufgerufen wird. Es wird die zu diesem Objekt gehörige Implementierung von __str__ verwendet. Unterklassen von Expression können daher unterschiedliche Implementierungen von __str__ bereitstellen und die von der Klasse Expression geerbte Methode __repr__ kann diese unterschiedlichen Implementierungen verwenden.
Die Klasse Number definieren wir wie folgt.
class Number(Expression):
def __init__(self, value):
self._value = value
def value(self):
return self._value
def __str__(self):
return str(self._value)
Es ist sinnvoll von Expression zu erben, damit Number-Objekte in python3 ordentlich angezeigt werden, ohne dass wir erneut die Methode __repr__ überschreiben müssen.
Zur Definition der Klassen Sum und Product definieren wir zunächst eine gemeinsame Oberklasse Binary wie folgt.
class Binary(Expression):
def __init__(self, left, right):
self._left = left
self._right = right
def left(self):
return self._left
def right(self):
return self._right
def __str__(self):
return "(" + str(self.left()) + self.op() + str(self.right()) + ")"
Im Konstruktor werden übergebene Argumente in Attributvariablen gespeichert. Die Methode __str__ definieren wir unter Verwendung einer Methode op, die von Unterklassen bereitgestellt werden muss. Die Methode value implementieren wir für die Klasse Binary nicht.
Die Unterklassen Sum und Product von Binary erben den Konstruktor der Oberklasse und berechnen den Wert zugehöriger Ausdrücke mit Hilfe entsprechender Methoden für die Argumente. Zusätzlich definieren sie die in der geerbten __str__ Methode verwendete Methode op.
class Sum(Binary):
def value(self):
return self.left().value() + self.right().value()
def op(self):
return "+"
class Product(Binary):
def value(self):
return self.left().value() * self.right().value()
def op(self):
return "*"
Die Definition der Hilfsklasse Binary vermeidet eine doppelte Implementierung der Textdarstellung.
Da Sie weder die value noch die op Methode implementiert, sollte sie nicht direkt instantiiert werden (sondern nur indirekt über Unterklassen, die alle benötigten Methoden implementieren.)1
Hausaufgabe: Klassen für Schachfiguren definieren
Der Klasse Piece fehlt eine Methode is_allowed, die aber bei Aufrufen der Methode move benötigt wird. Die Implementation der Klasse Piece ist insofern unvollständig. Da sich die Zugregeln für die Schachfiguren unterscheiden, muss is_allowed für die Unterklassen jeweils unterschiedlich definiert werden. Daher ist es nicht sinnvoll, diese direkt in Piece zu definieren.
Eine Klasse, deren Methoden unvollständig definiert sind, ist nicht geeignet, Objekte zu instanziieren, vielmehr dient Sie als Vorlage zur Definition der allen Unterklassen gemeinsamen Attribute und Methoden 1. So vermeidet man Redundanz in den Definitionen der Unterklassen.
class Rook(Piece):
def is_allowed(self,field):
return self.is_orthogonal(field)
def __str__(self):
return "Rook (" + self._color + ") at: " + self.position()
class Bishop(Piece):
def is_allowed(self,field):
return self.is_diagonal(field)
def __str__(self):
return "Bishop (" + self._color + ") at: " + self.position()
class Queen(Piece):
def is_allowed(self,field):
return self.is_orthogonal(field) or self.is_diagonal(field)
def __str__(self):
return "Queen (" + self._color + ") at: " + self.position()
Die Definition der Klasse Piece vermeidet eine mehrfache Implementierung der Methoden, die für alle Unterklassen gleich sind, indem die Methoden col, row, is_orthogonal, is_diagonal in Piece ergänzt werden:
class Piece:
def __init__(self, color, field):
self._color = color
self.set_position(field)
def position(self):
return self._position
def set_position(self, field):
self._position = field
def move(self, field):
if self.is_allowed(field):
self.set_position(field)
def row(self, pos):
return ord(pos[1]) - 49
def col(self, pos):
return ord(pos[0]) - 97
def is_orthogonal(self, field):
return self.row(self.position()) == self.row(field) \
or self.col(self.position()) == self.col(field)
def is_diagonal(self, field):
return self.row(self.position()) - self.col(self.position()) \
== self.row(field) - self.col(field) \
or self.row(self.position()) + self.col(self.position()) \
== self.row(field) + self.col(field)
def __repr__(self):
return str(self)
Der Aufruf von r.move(“a3”) auf einem Rook-Objekt ruft die Methode move der Überklasse auf, die ihrerseits die Methode is_valid der Rook-Klasse aufruft um schließlich mit set_position als Methode der Überklasse das Attribut _position des Rook-Objektes zu mutieren.
Mit diesem Mechanismus, der durch dynamische Bindung ermöglicht wird, lässt sich das unterschiedliche Verhalten verschiedener Piece-Unterklassen implementieren 2
-
Das Konzept abstrakter Klassen erlaubt die Definition von Klassen, die nicht direkt instantiiert werden können. ↩︎ ↩︎
-
Eine Methode ist polymorph, wenn sie mehrfach (in verschiedenen Klassen) mit der gleichen Signatur definiert ist, jedoch unterschiedlich implementiert ist. Beispiele sind
__str__undis_allowedin dieser Aufgabe. ↩︎
23. Rechnerarchitektur
23.1 Schaltnetze
Da Bits nur zwei Werte annehmen (Null oder Eins, Wahr oder Falsch, Strom an oder Strom aus), können Verknüpfungen von Bits mit Hilfe logischer Operationen realisiert werden. Auch Arithmetik ist durch Kombination logischer Operationen implementierbar, indem Zahlen im Binärsystem kodiert werden.
Logikgatter
Die Verknüfungstabellen der drei gängigsten logischen Operationen sind im Folgenden dargestellt:
Negation (not)
a |
not a |
|---|---|
| 0 | 1 |
| 1 | 0 |
Logisches Und (and)
a |
b |
a and b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Logisches Oder (or)
a |
b |
a or b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Negation (not) berechnet das jeweils entgegengesetzte Bit zur
Eingabe, Das Ergebnis der Konjunktion (and) ist genau dann
gesetzt, wenn beide Eingaben gesetzt sind, und das Ergebnis
der Disjunktion (or) ist genau dann nicht gesetzt, wenn keine
der Eingaben gesetzt ist.
Jede logische Operation kann durch geeignete Kombination
von not, and und or realisiert werden. Elektronische Bauteile,
die solche Verknüpfungen implementieren, heißen Gatter oder
Schaltnetze, wobei der Begriff Gatter vornehmlich für einfache
Schaltnetze verwendet wird.
Die bisher gezeigten Operationen können alle mit Hilfe der sogenannten nand (für not and) Operation implementiert werden. Alle Schaltnetze eines Computers können also allein aus NAND-Gattern gebaut werden. Die Verknüpfungstabelle der nand-Operation ist wie folgt definiert.
a |
b |
a nand b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Die Implementierung der anderen gezeigten Operation mit
Hilfe eines NAND-Gatters beschreiben wir mit Hilfe einer beispielhaft eingeführten Hardware-Beschreibungssprache. Gatter
haben Ein- und Ausgänge, die konzeptuell mit Leitungen verbunden werden können. Ein NAND-Gatter hat zwei Eingänge
und einen Ausgang. Verbinden wir die Eingänge mit Leitungen
a und b und den Ausgang mit einer Leitung out, schreiben
wir dies als NAND(a, b; out). Hierbei sind in der Parameter-Liste
Eingänge von Ausgängen durch ein Semikolon getrennt.
NOT(a; out):
NAND(a, a; out)
Konjunktion können wir nun mit Hilfe eines NAND- und
eines NOT-Gatters implementieren, denn a and b = not (a nand b):
AND(a, b; out):
NAND(a, b; c)
NOT(c; out)
Für die Disjunktion nutzen wir die Identität a or b = (not a) nand (not b):
OR(a, b; out):
NOT(a; c)
NOT(b; d)
NAND(c, d; out)
Eine häufig verwendete Verknüpfung ist xor (für exclusive
or), deren Ergebnis genau dann gesetzt ist, wenn die beiden
Argumente unterschiedliche Werte haben:
a |
b |
a xor b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Die xor-Verknüpfung kann wie folgt als Gatter realisiert werden:
XOR(a, b; out):
NOT(a; c)
NOT(b; d)
AND(a, d; e)
AND(c, b; f)
OR(e, f; out)
Diese Implementierung verwendet (indirekt) neun NAND- Gatter. Eine alternative Implementierung mit nur vier NAND- Gattern sieht wie folgt aus:
XOR(a, b; out):
NAND(a, b; c)
NAND(a, c; d)
NAND(c, b; e)
NAND(d, e; out)
Aus logischer Sicht ist nur das Ein-Ausgabe-Verhalten eines Gatters interessant. Allerdings beeinflusst die Anzahl der verwendeten Bauteile die Effizienz, da höhere Signallaufzeiten langsamere Berechnungen zur Folge haben.
Multiplexer
Weitere, für die Architektur von Digitalrechnern wichtige, Schaltnetze sind sogenannte Multiplexer, die es über einen Steuerungskanal ermöglichen zwischen verschiedenen Eingängen auszuwählen. Ein 2-zu-1 Multiplexer, wählt zum Beispiel zwischen zwei Eingangs-Bits mit Hilfe eines Steuerungs-Bits aus (setzt also je nach Wert des Steuerungs-Bits den einen oder den anderen Eingang auf den Ausgang).
Die Wahrheitstabelle eines 2-zu-1-Multiplexer mit den Eingangsbits a und b und dem Steuerungsbit x sieht folgendermaßen aus:
x |
a |
b |
out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Wenn das Steuerungsbit x auf 0 gesetzt worden ist, wird das Eingangsbit a zum Ausgang weitergeleitet, sonst das Bit b.
Multiplexer können zu größeren Multiplexern zusammengeschaltet werden. Zum Beispiel kann ein 4-zu-1-Multiplexer wie folgt aus drei 2-zu-1-Multiplexern zusammengebaut werden.
4MUX1(x, y, a, b, c, d; out):
2MUX1(y, a, b; e)
2MUX1(y, c, d; f)
2MUX1(x, e, f; out)
Hierbei wird je nach Wert der Steuerungs-Bits x und y einer der Eingänge a bis d auf den Ausgang out geleitet. Die
Implementierung des Gatters 2MUX1 ist eine Übungsaufgabe.
In Computern werden Bits in der Regel gebündelt verarbeitet. Bündelungen aus mehreren Bits heißen Bus und sind in der Regel 8, 16, 32, usw. Bits breit, um sie per Multiplexer effizient steuern zu können. Digitale Multiplexer können \(2^n\) Eingänge verarbeiten, wenn \(n\) die Anzahl der Steuerungsbits ist.
Arithmetikgatter
Schaltnetze können nicht nur logische sondern auch arithmetische Operationen ausführen, indem Zahlen als Bitfolgen, also im Binärsystem, dargestellt werden. Die folgende Tabelle zeigt die Zahlen von eins bis zehn im Unär-, Dezimal- und im Binärsystem mit drei Stellen:
| Anzahl (Unär) | Dezimal | Binär |
|---|---|---|
| # | 1 | 001 |
| ## | 2 | 010 |
| ### | 3 | 011 |
| #### | 4 | 100 |
| ##### | 5 | 101 |
| ###### | 6 | 110 |
| ####### | 7 | 111 |
| ######## | 8 | Überlauf |
| ######### | 9 | Überlauf |
| ########## | 10 | Überlauf |
Addition mit Binärzahlen folgt dem gleichen Verfahren wie Addition von Zahlen in anderen Zahlensystemen: Zahlen werden stellenweise addiert, wobei Überträge zur nächsthöheren Stelle übernommen werden. Das folgende Beispiel illustriert die Addition der Zahlen zwei und drei im Binärsystem mit drei Stellen.
010
+ 011
ü 1
-----
101
Das Ergebnis ist die Binärdarstellung der Zahl fünf.
Zur Implementierung binärer Addition durch ein Schaltnetz implementieren wir zunächst ein Gatter HADD (für half adder), das aus zwei Eingangs-Bits das Ergebnis-Bit und das Übertrags- Bit berechnet:
HADD(a, b; sum, carry):
XOR(a, b; sum)
AND(a, b; carry)
Ein ADD-Gatter benötigt ein zusätzliches Eingabe-Bit für den Übertrag der nächst-niedrigeren Stelle. Die Definition des ADD-Gatters ist eine Übungsaufgabe. Zur Addition von Binärzahlen mit \(n\) Stellen können dann \(n\) ADD-Gatter hintereinander geschaltet werden.
Arithmetisch-logische Einheit (ALU)
Die arithmetisch-logische Einheit (ALU für Arithmetic-Logic Unit) ist das komplexeste Schaltnetz im Hauptprozessor eines Computers. Sie kombiniert Implementierungen verschiedener logischer und arithmetischer Operationen, die über Steuerungs-Bits (ähnlich wie bei einem Multiplexer) ausgewählt werden können. Verschiedene Prozessoren unterscheiden sich in Art und Anzahl durch die ALU implementierter Operationen. Hierbei werden Prozessoren mit wenigen effizienten Instruktionen (RISC für Reduced Instruction Set Computer) von solchen mit vielen maßgeschneiderten Instruktionen (MISC für Multiple Instruction Set Computer) unterschieden. Der Vorteil der RISC-Architektur ist, dass die Signalverzögerung durch die ALU geringer ist, weil diese weniger Instruktionen zur Verfügung stellen muss. Der Vorteil der MISC-Architektur ist, dass sie Instruktionen, die durch mehrere RISC-Instruktionen modelliert werden müssten, direkt in Hardware und damit effizienter implementiert.
Die Ein- und Ausgabe der ALU ist mit Registern und dem Hauptspeicher verbunden, die Steuerungs-Bits werden mit Hilfe eines speziellen Registers namens Programmzähler bestimmt. Speicher und Programmzähler werden im nächsten Abschnitt behandelt. Sie sind der Schlüssel dazu, komplexe Instruktionen auf Basis der primitiven, von der ALU bereitgestellten, Instruktionen zu implementieren und deshalb ein wichtiges Abstraktionskonzept zur Realisierung von Computern.
23.1.1 Übungsaufgaben
Aufgabe: Logische Operationen programmieren
Definieren Sie in Python
- eine Funktion
nicht, - eine Funktion
undsowie - eine Funktion
oder
ohne vordefinierte logische Operationen (wie not, and, or oder Vergleichsoperatoren) zu verwenden. Bedingte Anweisungen sind dabei erlaubt.
Die Funktionen sollen jeweils die entsprechenden logischen Operationen implementieren, also Wahrheitswerte als Argumente erwarten und als Ergebnisse liefern. Die Funktion nicht entspricht also der Negation, und der Konjunktion und oder der Disjunktion.
Aufgabe: Binärzahlen konvertieren
Schreiben Sie eine Python-Funktion decimal, die eine als Zeichenkette dargestellte Binärzahl als Argument erwartet und die entsprechende Dezimalzahl zurück liefert. Zum Beispiel soll der Aufruf decimal("101010") als Ergebnis 42 liefern.
Aufgabe: 2-zu-1 Multiplexer definieren
Ein 2-zu-1 Multiplexer kann als logisches Gatter mit drei Eingängen und einem Ausgang definiert werden. Definieren Sie unter Verwendung unserer Hardware-Beschreibungssprache ein 2MUX1-Gatter auf Basis der bisher definierten Gatter. Wieviele NAND-Gatter werden von Ihrer Implementierung (direkt oder indirekt) verwendet?
Aufgabe: Volladdierer definieren
Definieren Sie ein Gatter ADD mit den Eingängen a, b und cin sowie den Ausgängen sum und cout zur Addition der drei Eingänge mit Übertrag. Geben Sie zunächst die Verknüpfungstabelle der Additions-Operation an. Verwenden Sie zur Implementierung des Gatters den in der Vorlesung definierten Halbaddierer um die Definition zu vereinfachen.
Aufgabe: LogiSim verwenden
Machen Sie sich mit Logisim vertraut und verwenden Sie es, um einige der in der Vorlesung vorgestellten Gatter und Schaltnetze zu definieren. Verwenden Sie auch die Funktion zur Analyse definierter Schaltkreise und zur automatischen Generierung.
Bonusaufgabe: Rechenwerk simulieren
In dieser Aufgabe sollen Sie ein Rechenwerk (englisch: arithmetic logic unit - ALU) in Logisim simulieren.
Ein Rechenwerk ist das komplexeste Schaltnetz in einem Prozessor. Unter Rückgriff auf ausgewählte, vorher zu definierende, Gatter und Schaltnetze ist es aber mit überschaubarem Aufwand möglich, ein einfaches Rechenwerk, das jedoch alle wichtigen Operationen beherrscht, zu entwickeln. Das in dieser Aufgabe zu definierende Rechenwerk soll zwei Eingangssignale zu einem Ausgangssignal kombinieren. Ein- und Ausgangssignale sind dabei jeweils ein Bus, kombinieren also mehrere Bits, so dass zum Beispiel auch Zahlen dargestellt werden können. Welche Operation vom Rechenwerk ausgeführt wird, wird dabei von zusätzlichen Eingangssignalen bestimmt. Zusätzliche Ausgangsignale zeigen Eigenschaften des Ausgangssignals an.
Es zeigt sich, dass eine Reihe nützlicher Operationen sich auf Kombinationen deutlich einfacherer Operation auf den Ein- und Ausgangssignalen ausdrücken lassen. Ein bemerkenswert eleganter Entwurf eines Rechenwerks findet sich im Kursmaterial From NAND to Tetris. Kapitel 2 über Arithmetische Schaltkreise enthält auch eine Beschreibung eines Rechenwerks, die sie in dieser Aufgabe implementieren sollen.
23.2 Synchrone Schaltwerke
Prinzipiell lässt sich jede von einem Computer ausführbare Operation durch ein Schaltnetz realisieren. Allerdings wäre es unpraktisch, für jede Anwendung eigens spezielle Hardware anzufertigen. Ein großer Vorteil gängiger Computer ist ihre Vielseitigkeit. Sie erlauben eine unbegrenzte Zahl unterschiedlicher Operationen mit Hilfe von Software zu realisieren. Die begrenzte Anzahl der von der ALU bereitgestellten Operationen reicht dazu aus.
Der dabei entscheidende Mechanismus ist es, mehrere Instruktionen nacheinander auszuführen und dabei auftretende Zwischenergebnisse zu speichern. Statt Schaltnetze hintereinanderzuschalten, um komplexe Instruktionen auszuführen, kann dabei das Ergebnis der ersten Operation gespeichert und dann mit dem selben Schaltnetz weiter verarbeitet werden.
Diesem Mechanismus liegt ein Konzept zugrunde, das wir bei Schaltnetzen bisher nicht berücksichtigt haben: das der Zeit. Instruktionen werden zeitlich nacheinander ausgeführt und zu einem Zeitpunkt gespeicherte Werte können zu einem späteren Zeitpunkt abgefragt werden.
Zeit wird in Computern durch ein periodisches Signal modelliert. Eine Periode des Signals entspricht dabei einem Taktzyklus des Hauptprozessors. Ein Taktzyklus muss lang genug für die Signallaufzeiten aller beteiligten Schaltnetze sein. Ist dies gegeben, brauchen wir die einzelnen Signallaufzeiten nicht mehr zu berücksichtigen, um das Verhalten eines Computers zu erklären.
Flip-Flops
Schaltnetze, die zusätzlich zu ihren logischen Eingängen auch auf das Taktsignal zugreifen, heißen synchrone Schaltwerke. Wie bei den Schaltnetzen gibt es auch hier ein primitives Bauteil, dass allen synchronen Schaltwerken zugrunde gelegt werden kann: das Flip-Flop. Die Implementierung eines Flip-Flop ist aus informatischer Sicht uninteressant. Wir begnügen uns damit, sein Verhalten zu beschreiben und für die Implementierung komplexerer synchroner Schaltwerke zu nutzen.
Das Verhalten eines Flip-Flops ist einfach zu beschreiben. Es hat (neben dem Eingang für das Taktsignal) einen Eingang und einen Ausgang, wobei der Ausgang immer das Eingangssignal aus dem vorigen Taktzyklus liefert.
Speicher
Ein 1-Bit-Register ist der kleinste aller Speicherbausteine. Es
hat (neben einem Eingang für das Taktsignal) zwei Eingänge in
und load und einen Ausgang out. Wenn das load-Bit gesetzt ist,
wird der an in anliegende Wert gespeichert. Der Wert von out ist
immer der momentan gespeicherte Wert. Ist das load-Bit nicht
gesetzt, bleibt der Wert aus dem vorigen Taktzyklus gespeichert.
Die Implementierung eines 1-Bit-Registers verwendet ein Flip-Flop und einen 2-zu-1 Multiplexer, der je nach load-Eingang zwischen dem Eingang und dem Ausgang auswählt.
Reg1(clock, load, in; out):
2MUX1(load, out, in; a)
FlipFlop(clock, a; out)
Dadurch wird bei gesetztem load-Bit der Eingang des Registers auf den Eingang des Flip-Flops gelegt. Ist das load-Bit nicht gesetzt, wird das Flip-Flop mit seinem Ausgang verbunden, wodurch der Wert aus dem vorigen Taktzyklus gespeichert bleibt.
Register der Wortgröße \(w\) können aus \(w\) 1-Bit-Registern zusammengeschaltet werden. Ein- und Ausgang werden dabei zu einem Bus der Wortgröße \(w\), deren Zustand bei gesetztem load-Bit komplett im Register abgelegt wird.
Der Hauptspeicher eines Computers kann wiederum aus mehreren Registern der Wortgröße \(w\) zusammengesetzt werden. Ein- und Ausgang behalten dabei die Größe \(w\) und werden durch einen Adressierungs-Eingang erweitert, der mit Hilfe eines De-Multiplexers bestimmt, in welchem Register die angelegte Bit-Kombination abgespeichert werden soll. De-Multiplexer sind wie umgedrehte Multiplexer, leiten also ein Eingangssignal gemäß angelegter Steuerungs-Bits auf einen von mehreren möglichen Ausgängen um. Der Ausgang des Hauptspeichers ergibt sich mit Hilfe eines Multiplexers aus dem Ausgang des addressierten Registers.
Instruktionsspeicher und Programmzähler
Das vom Computer ausgeführte Programm wird in einem speziellen Bereich des Hauptspeichers (dem sogenannten Instruktionsspeicher) abgelegt, ist also nichts weiter als eine speziell interpretierte Bitfolge. Der Einfachheit halber können wir annehmen, dass jede Maschineninstruktion in einem Register des Instruktionsspeichers abgelegt ist.
Typischerweise gibt es zwei Arten von Maschineninstruktionen, die zum Beispiel durch ihr erstes Bit voneinander unterschieden werden können.
LOAD-Instruktionen erlauben, einen vorgegebenen Wert in einem Register des Hauptprozessors abzuspeichern- Andere Instruktionen bestehen aus Steuerungs-Bits für die ALU und Adressierungs-Bits für die Ein- und Ausgabe der von der ALU ausgeführten Operation.
Die Ausführung des im Instruktionsspeicher enthaltenen Programms steuert der sogenannte Programmzähler, der die Adresse der als Nächstes auszuführenden Instruktion enthält. Der Programmzähler ist ein Register, kann also (insbesondere durch sogenannte JUMP-Instruktionen) auf eine beliebige Adresse gesetzt werden und diese speichern. Zusätzlich verfügt er in der Regel über Eingänge reset und inc. Ist das reset-Bit gesetzt, wird der Zähler auf Null zurückgesetzt. Ein angelegtes inc-Bit hat zur Folge, dass der Zähler erhöht wird, also auf die nächste Instruktion im Instruktionsspeicher zeigt.
23.3 Hauptprozessor und Von-Neumann-Architektur
Ein Computer nach Von-Neumann-Architektur besteht im Wesentlichen aus einem Hauptprozessor und einem Hauptspeicher, die über ein Bus-System verbunden sind.
Der Hauptprozessor besteht aus der ALU, aus Registern (auf die schneller zugegriffen werden kann als auf den Hauptspeicher) sowie aus einer Steuerungseinheit bestehend aus Programmzähler und einem Schaltnetz, dass die ausgeführte Maschineninstruktion mit Hilfe der ALU verarbeitet und dabei Ein- und Ausgabe der ALU geeignet adressiert. In der Regel wird nach einer Instruktion der Programmzähler erhöht, um die nächste Instruktion auszuführen. Bei Sprungbefehlen wird er stattdessen auf die in der Instruktion angegebene Sprungadresse gesetzt.
Alle Komponenten eines Computers können letztendlich auf NAND-Gatter und Flip-Flops zurückgeführt werden. NAND- Gatter zu komplexen Schaltnetzen zusammenzuschalten ist ein wesentliches Abstraktionsmittel, um Operationen auf Binärdaten in Hardware zu realisieren. Schaltnetze mit Flip-Flops zu synchronen Schaltwerken zu kombinieren ist das andere wesentliche Abstraktionsmittel für den Bau von Computern, denn es ermöglicht, Ergebnisse zu speichern und komplexe Instruktionen durch Hintereinader-Ausführung einfacherer Instruktionen zu implementieren.
Memory Mapped I/O
Das bisher vorgestellte Rechner-Modell bietet scheinbar keine Möglichkeit, Daten in den Computer einzugeben oder von diesem ausgeben zu lassen. Für eine informationsverarbeitende Maschine, deren einzige Aufgabe es ist, Eingabe-Information in Ausgabe-Information zu transformieren, erscheint das als ein nicht unerheblicher Nachteil.
Glücklicherweise brauchen wir die bisher vorgestellte Architektur konzeptuell nicht zu erweitern, um Ein- und Ausgabe von Daten zu ermöglichen. Durch sogenanntes Memory-Mapped I/O (I/O für Input/Output) kann der Computer auf Ein- und Ausgabegeräte zugreifen, wie auf den Hauptspeicher und so Daten einlesen oder ausgeben. Dabei wird einem angeschlossenen Gerät ein festgelegter Speicherbereich zugewiesen, der zu jedem Zeitpunkt den aktuellen Zustand des Geräts reflektiert.
Zum Beispiel kann einer Tastatur ein Register des Hauptspeichers zugeordnet werden, in dem zu jedem Zeitpunkt eine binäre Kodierung der gerade gedrückten Taste abgelegt wird. Der Computer kann dann durch Lesen dieses Registers Tastatureingaben verarbeiten.
Zur Ausgabe kann einem Bildschirm ein festgelegter Speicherbereich (zum Beispiel mit einem Register pro Bildpunkt) zugeordnet werden. Der Computer kann dann durch Schreiben in diesen Speicherbereich Ausgaben auf dem Bildschirm erzeugen.
23.4 Assembler
Algorithmen, die in Programmiersprachen formuliert sind, müssen in Maschineninstruktionen übersetzt werden, um auf einem Computer ausgeführt zu werden. Diese Aufgabe wird in der Regel von einem anderen (Compiler genannten) Programm ausgeführt. Manche Programmiersprachen (zum Beispiel C) erlauben es, sogenannte Assembler-Sprache in Programme einzubetten, um (zum Beispiel aus Effizienz-Gründen) Einfluss auf die generierten Maschineninstruktionen zu nehmen.
Als Assembler-Sprache wird eine aus den Maschineninstruktionen eines Computers abgeleitete Programmiersprache bezeichnet. Jedes Computer-Modell hat seine eigene Assembler- Sprache, die die zugrunde liegenden Maschineninstruktionen widerspiegelt. Assembler-Sprache erlaubt eine textuelle Eingabe von Maschineninstruktionen, wobei symbolische Namen für Speicheradressen benutzt werden können. Der Compiler, der Assembler-Sprache in Maschineninstruktionen übersetzt, heißt Assembler.
Als ein Beispiel für ein in (imaginärer) Assembler-Sprache geschriebenes Programm betrachten wir das folgende Programm, das die Zahlen von 1 bis 100 addiert.
i = 1
sum = 0
LOOP:
if i = 101 goto END
sum = sum + i
i = i + 1
goto LOOP
END:
Die Symbole i und sum werden vom Assembler in Adressen
für den Hauptspeicher (oder im Hauptprozessor enthaltene Register) übersetzt. Welche Adressen dafür verwendet werden, ist
für das Verhalten des Programms irrelevant, solange sie eindeutig sind. Die Symbole LOOP und END, die in Sprungbefehlen
verwendet werden, werden vom Assembler in die Adresse des Instruktionsspeichers übersetzt, in die die nach ihnen deklarierte
Instruktion geschrieben wird.
Zum Vergleich betrachten wir noch einen Ausschnitt aus einem realen Assembler-Programm, das dieselbe Aufgabe löst. Es ist dadurch entstanden, dass ein in C geschriebenes Programm in die Assembler-Sprache eines 64-Bit-Linux-Rechners übersetzt wurde:
movl $1, -8(%rbp) # entspricht i = 1
movl $0, -4(%rbp) # entspricht sum = 0
jmp .L2 # springe zu .L2
.L3: # .L3 entspricht der Wiederholung
movl -8(%rbp), %eax # lade i ins Register eax
addl %eax, -4(%rbp) # entspricht sum = sum + i
addl $1, -8(%rbp) # entspricht i = i + 1
.L2: # .L2 ist die Abfrage der Bedingung
cmpl $101, -8(%rbp) # vergleiche i mit 101
jne .L3 # falls ungleich, springe zu .L3
23.5 Quellen und Lesetipps
- From NAND to Tetris: Building a Modern Computer from First Principles
- John von Neumann: The First Draft Report on the EDVAC]
- Edsger W. Dijkstra: Wie unwichtig es ist, ob U-Boote schwimmen können (niederländisch)
- Ein für schulische Zwecke didaktisch reduzierter Modellrechner mit Pseudoassemblersprache: MoPs
23.6 Lösungen
Lösungen
Aufgabe: Logische Operationen programmieren
Wir können alle Funktionen mit Hilfe einer einzigen bedingten Verzweigung definieren.
def nicht(x):
if x:
return False
else:
return True
def und(x, y):
if x:
return y
else:
return False
def oder(x, y):
if x:
return True
else:
return y
Hier sind alternative Definitionen mit optionalen Anweisungen (ohne else-Zweig):
def nicht1(x):
if x:
return False
return True
def und1(x, y):
if x:
if y:
return True
return False
def oder1(x, y):
if nicht(x):
if nicht(y):
return False
return True
Die und- und oder- Funktionen können wir mit Hilfe der De Morganschen Gesetze auch mit Hilfe der jeweils anderen Operation ausdrücken.
def und2(x, y):
return nicht(oder(nicht(x), nicht(y)))
def oder2(x, y):
return nicht(und(nicht(x), nicht(y)))
Aufgabe: Binärzahlen konvertieren
def decimal(b):
n = 0
for i in range(0, len(b)):
n = n + 2**i * int(b[len(b)-i-1])
return n
Aufgabe: 2-zu-1 Multiplexer definieren
Wenn x Null ist, hat der Ausgang out des gesuchten Bauteils den selben Wert wie der
Eingang a; wenn x Eins ist, hat out den selben Wert wie b.
Dieses Verhalten wird auch durch die Gleichung out = (not x and a) or (x and b) beschrieben: Der Ausgang out ist genau dann gesetzt, wenn
x nicht gesetzt ist und a gesetzt ist oder wenn x und b beide
gesetzt sind.
Die folgende Implementierung des 2MUX1-Gatters, setzt diese Formel als Hardware-Beschreibung um.
2MUX1(x,a,b;out):
NOT(x;y)
AND(y,a;c)
AND(x,b;d)
OR(c,d;out)
Die Eingänge sind in den Parameterlisten von den Ausgängen durch ein Semikolon getrennt.
Da das NOT-Gatter ein NAND-Gatter enthält, das AND-Gatter zwei und das OR-Gatter drei, besteht der so definierte Multiplexer insgesamt aus acht NAND-Gattern.
Aufgabe: Volladdierer definieren
Die Verknüpfungstabelle eines ADD-Gatters zur Addition der Eingänge
a, b und cin (für input carry) mit den Ausgängen sum
und cout (für output carry) sieht wie folgt aus.
| a | b | cin | sum | cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Der Summen-Ausgang sum ergibt sich dabei als Summe der drei Eingänge, die nacheinander mit zwei Halbaddierern berechnet werden kann. Der Übertrags-Ausgang cout ist genau dann gesetzt, wenn bei (mindestens) einer dieser Additionen ein Übertrag auftritt. Wir können ihn also mit einem OR-Gatter aus den beiden Überträgen der Halbaddierer berechnen.
Die folgende Implementierung des ADD-Gatters implementiert diese Idee.
ADD(a,b,cin;sum,cout):
HADD(a,b;s1,c1)
HADD(s1,cin;sum,c2)
OR(c1,c2;cout)
Zur Addition von \(n$-stelligen Binärzahlen können nun $n\) so definierte ADD-Gatter hintereinander geschaltet werden.
Bonusaufgabe: Rechenwerk simulieren
Diese Lösung beschreibt das Rechnewerk mit Hilfe unserer Hardware-Beschreibungs-Sprache.
Die folgenden Definitionen fassen logische Gatter zusammen, die wir zur Definition des Rechenwerks verwenden werden. Alle gezeigten Gatter werden wir auch so verwenden, dass statt Bits Busse als Argumente verwendet werden. Das ist so zu verstehen, dass die einzelnen Bits komponentenweise (entsprechend ihres Index im Reißverschlussverfahren) verknüpft werden. Zusätzlich werden wir eine Variante OR(ins;out) des OR-Gatters verwenden, bei dem das out-Bit die Oder-Verknüpfung aller Bits des Busses ins darstellt.
NOT(a;out):
NAND(a,a;out)
AND(a,b;out):
NAND(a,b;c)
NOT(c;out)
OR(a,b;out):
NOT(a;x)
NOT(b;y)
NAND(x,y;out)
XOR(a,b;out):
NAND(a,b;x)
NAND(a,x;y)
NAND(b,x;z)
NAND(y,z;out)
MUX(a,b,sel;out):
NOT(sel;nsel)
AND(nsel,a;u)
AND(sel,b;v)
OR(u,v;out)
Die folgenden Definitionen fassen arithmetische Schaltnetze zusammen, die wir verwenden werden. Zusätzlich werden wir ein Schaltnetz ADD(as,bs;outs) verwenden, das auf Basis des Voll-Addierers FADD definiert werden kann, mit dem die als Bus gleicher Größe dargestellten Argumente verknüpft werden, wobei das letzte Übertragsbit ignoriert wird.
HADD(a,b,;sum,carry):
XOR(a,b;sum)
AND(a,b;carry)
FADD(a,b,cin;sum,cout):
HADD(a,b,;s,c1)
HADD(s,cin;sum,c2)
OR(c1,c2;cout)
Auf Basis dieser Definitionen können wir nun das Rechenwerk definieren. Es kombiniert die (Mehrbit-) Eingangssignale x und y zum (Mehrbit-) Ausgangssignal out. Welche Operation ausgeführt werden soll, wird durch die folgenden zusätzlichen Eingangssignale bestimmt:
zx(zero x) zeigt an, ob stattxein Nullsignal verwendet werden soll.nx(negate x) zeigt an, obx(bitweise) negiert werden soll.zyundnyzeigen entsprechende Operationen auf dem Eingangyan.f(function) zeigt an, ob die so entstehenden Signale durch Konjunktion oder Addition verknüpft werden sollen.no(negate output) zeigt an, ob der Ausgang (bitweise) negiert werden soll.
Die zusätzlichen Ausgänge zr (zero) und ng (negative) des Rechenwerks zeigen an, ob das Ergebnis Null oder negativ ist. Zur verwendeten Binärdarstellung negativer Zahlen empfliehlt sich die Lektüre des in der Aufgabenstellung angesprochenen Kapitels zu Arithmetischen Schaltkreisen.
Der Bus zero besteht aus Null-Bits. Die Schreibweise bus[i] steht für das i-te Bit des Busses bus.
ALU(x,y,zx,nx,zy,ny,f,no;out,zr,ng):
# The zx and zy bits determine whether the corresponding inprint are zeroed.
MUX(x,zero,zx;x_zero)
MUX(y,zero,zy;y_zero)
# The nx and ny bits determine whether inprint are bitwise negated.
NOT(x_zero;x_not)
NOT(y_zero;y_not)
MUX(x_zero,x_not,nx;x_mod)
MUX(y_zero,y_not,ny;y_mod)
# The ALU combines (possibly modified) inprint using conjunction or addition.
AND(x_mod,y_mod;out_and)
ADD(x_mod,y_mod;out_add)
MUX(out_and,out_add,f;o)
# The output is bitwise negated if the no bit is set.
NOT(o;o_not)
MUX(o,o_not,no;out)
# The zr output bit is set if the output is zero.
OR(out;nzr)
NOT(nzr;zr)
# The ng output bit is set if the output is negative.
AND(out[0],out[0],ng)
24. Netzwerke
24.1 Netzwerkdienste und -protokolle
Netzwerkdienste
Die Post transportiert Sendungen von Absendern zu Empfängern. Dabei gibt es festgelegte Formate für Briefe, Päckchen und Pakete. Auch ist festgelegt, wie und wo Absender und Empfängeradressen zu notieren sind. Der Standardversand garantiert nicht, bis wann oder dass Sendungen überhaupt ankommen. Per Expressversand und Einschreiben kann die Zustellung beschleunigt und garantiert werden.
In Computernetzen verhält es sich ganz ähnlich. Auch hier werden Formate für den Austausch von Daten definiert, die Adressierung folgt festgelegten Regeln und unterschiedliche Netzwerdienste unterscheiden sich bezüglich der zugesicherten Dienstgüte. Ein interessanter Aspekt ist dabei die automatische Fehlererkennung und -Korrektur zur Bereitstellung verlässlicher Dienste.
In Computernetzen wird zwischen verbindungslosen und verbindungs-orientierten Diensten unterschieden. Verbindungslose Dienste funktionieren ähnlich wie die Post. Sie unterscheiden sich bezüglich ihrer Verlässlichkeit, also danach, ob Nachrichten
-
verloren gehen (oder dupliziert),
-
während des Transprts verfälscht,
-
oder in ihrer Reihenfolge vertauscht
werden können.
Verbindungs-orientierte Dienste funktionieren ähnlich wie das Telefon. Dem sogenannten Verbindungsaufbau folgt der Datenaustausch vor dem Verbindungsabbruch. Die Kommunikation während des Datenaustauschs erfolgt entweder nur ein eine Richtung (simplex) oder in beide Richtungen (duplex).
Das Internet stellt einen verbindungslosen Kommunikationsdienst bereit. Es gibt jedoch Anwendungen, die auf Basis des Internets verbindungs-orientierte Dienste bereitstellen (z.B. Internettelefonie).
Netzwerkprotokolle
Die Regeln, nach denen die Kommunikation in Netzwerken abläuft, werden in Protokollen definiert. Protokolle spezifizieren zum Beispiel Datenformate und Adressierungsschemata sowie Mechanismen zur Weiterleitung von Nachrichten oder zur Fehlerkorrektur. Auch Mechanismen zum Aushandeln von Übertragungsparametern oder zum Verbindungsauf- und Abbau sind Teil von Protokollen.
Um verschiedene Aspekte der Kommunikation zu entkoppeln sind Netzwerkprotokolle hierarchisch in sogenannten Schichten strukturiert, die aufeinander aufbauen. Dieses Vorgehen ähnelt der Ausführung von Programmen auf einem Rechner, wo Programme zunächst in Assemblersprache übersetzt werden, und die Assemblerprogramme schließlich in Maschinensprache. Auch die Abstraktion von Algorithmen durch Funktionen und Prozeduren folgt insofern einem ähnlichen Muster, als zur Verwendung einer Funktion oder Prozedur ihre Implementierung nicht bekannt zu sein braucht.
Unterschiedliche Netzwerkprotokolle ordnen sich in der Regel in eine der folgenden Schichten ein, je nachdem welche Funktionalität der Kommunikation sie implementieren.
-
Die Verbindungsschicht umfasst Protokolle zur Übertragung von Bitfolgen über ein physikalisches Transportmedium. Die übertragenen Daten als Bitfolgen zu interpretieren ist bereits eine Abstraktion des eigentlichen über das Transportmedium verschickten Signals.1 Ein wichtiger Aspekt von Protokollen dieser Schicht ist die Erkennung und Korrektur von Übertragungsfehlern. Häufig eingesetzte Protokolle in dieser Schicht sind Ethernet oder WLAN.
-
Die Vernetzungsschicht umfasst Protokolle zur Weiterleitung von Nachrichten durch räumlich getrennte Netzwerke. Alle beteiligten Netze müssen dazu natürlich physikalisch verbunden sein. Es ist jedoch möglich, eine Nachricht über unterschiedliche Transportmedien weiter zu leiten. Ein wichiger Aspekt von Protokollen dieser Schicht sind Mechanismen zur Etablierung eines Weges vom Sender zum Empfänger über verschiedene physikalische Netzwerke hinweg. Im Internet wird diese Schicht von dem Internetprotokoll (IP) implementiert.
-
Die Transportschicht umfasst Protokolle zur Etablierung gewisser Gütekriterien für die Übertragung von Nachrichten. Insbesondere werden Übertragungsfehler der Vernetzungsschicht durch Mechanismen kompensiert, die die verlässliche Übertragung von Nachrichten gewährleisten. Im Internet wird diese Schicht in der Regel vom Transmission Control Protocol (TCP) implementiert.
-
Die Anwendungsschicht umfasst Protokolle zum anwendungsspezifischen Nachrichtenaustausch. Ein im Internet häufig eingesetztes Protokoll dieser Schicht ist das HyperText Transfer Protocol (HTTP) zur Übertragung von Webseiten über das Internet. Auch Protokolle wie SMTP, POP oder IMAP zur Übertragung von Emails, FTP zum Dateitransfer oder Protokolle zur Internettelefonie gehören in diese Schicht.
Die Unterteilung der Protokolle in die vier genannten Schichten ist ein wichtiger Mechanismus zur Abstraktion der bereitgestellten Dienste. So brauchen sich Protokolle der Anwendungsschicht nicht darum zu kümmern, über welches Medium Daten transportiert werden oder wie sie vom Sender zum Empfänger gelangen. Umgekehrt ist es den Protokollen der Verbindungsschicht egal, welche Art von Daten sie über ein Transportmedium transportieren, ob es sich also zum Beispiel um Webseiten oder Videodaten handelt.
Das Internet umfasst Protokolle von der Vernetzungs- bis zur Anwendungsschicht, die wir exemplarisch in folgenden Abschnitten behandeln werden. Zunächst schauen wir uns jedoch noch wichtige Aspekte der Verbindungsschicht an.
Media Access Control und Fehlererkennung
Lokale Netzwerke sind in der Regel Bus-Netze, in denen also alle Rechner mit einem gemeinsamen Transportmedium verbunden sind. Im Ethernet sind Computer mit zusammengeschalteten Kabeln verbunden, im WLAN teilen sie sich einen gemeinsamen Funkkanal.
Bei gemeinsamer Nutzung eines Transportmediums können sogenannte Kollisionen auftreten, wenn mehrere Parteien gleichzeitig versuchen, Daten zu senden. Mechanismen zur Media Access Control (MAC) dienen dazu, Kollisionen zu behandeln. Sogenannte pessimistische Verfahren versuchen dabei Kollisionen von vornherein zu vermeiden, während optimistische Verfahren versuchen, geeignet auf entstandene Kollisionen zu reagieren.
Im Ethernet oder WLAN werden Computer über eine sogenannte MAC-Adresse eindeutig identifiziert. Das Format zum Austausch von Daten im Ethernet besteht im Wesentlichen aus einem Header, der die Absender- und Empfängeradresse enthält, gefolgt den eigentlichen Nutzdaten und einer Prüfsumme zur Fehlerbehandlung.
Eine Prüfsumme ist eine Methode, um Übertragungsfehler durch Redundanz zu erkennen. Als vereinfachtes Beispiel dieses Prinzips könnten wir jeder Nachricht ein Bit anhängen, dass angibt, ob die Nutzdaten eine gerade oder eine ungerade Anzahl von Einsen enthalten. Beim Dekodieren der Nachricht können (manche) Übertragungsfehler dann daran erkannt werden, dass das angehängte Bit nicht zu der empfangenen Anzahl von Einsen passt.
Zum Beispiel könnten wir die Nachricht
011011
durch eine angehängte 0 ergänzen, die anzeigt, dass sie eine gerade
Anzahl von Einsen enthält:
0110110
Dadurch ist sicher gestellt, das gesendete Nachrichten immer eine gerade Anzahl von Einsen enthalten. Denn wenn die Anzahl ursprünglich ungerade ist, wird ja eine zusätzliche Eins angehängt. Angenommen, die obige Nachricht würde bei der Übertragung wie folgt verfälscht:
0100110
Der Empfänger würde dann einen Übertragungsfehler daran erkennen, dass die Anzahl der Einsen in der empfangenen Nachricht ungerade ist. Anhand dieser Information kann der Empfänger den Fehler zwar erkennen aber nicht korrigieren, da nicht klar ist, an welcher Stelle der Fehler auftrat.
Auch werden nicht alle Übertragungsfehler auf diese Weise erkannt. Wenn zum Beispiel mehr als ein Bit verfälscht wird, kann es passieren, dass der Fehler nicht erkannt wird (zum Beispiel, wenn genau zwei Einsen jeweils durch Nullen ersetzt werden oder umgekehrt). Um mehr Fehler zu erkennen, kann die Prüfsumme verlängert werden. Zum Beispiel könnten wir zwei Bits anhängen, die dem Rest bei der Division durch vier entsprechen. Die Nachricht
010100
würde also wie folgt verlängert, da “10” die Binärdarstellung des Restes der Division von zwei durch vier ist.
01010010
Diese Methode erlaubt es mehr, wenn auch noch immer nicht alle, Übertragungsfehler zu erkennen. Zum Beispiel würden wir erkennen, wenn zwei Nullen in der ursprünglichen Nachricht durch Einsen ersetzt würden, da dann die Anzahl zwar noch immer durch zwei aber nun auch durch vier teilbar wäre.
-
Bits (also Nullen und Einsen) als elektrisches Signal in Kupferkabeln, optisches Signal in Glasfaserkabeln oder Funk-Signal zur Drahtlosübertragung zu konvertieren, ist nicht Teil der Informatik sondern (ähnlich wie die physikalische Realisierung von Schaltwerken) Teil der Elektro- bzw. Nachrichtentechnik. ↩︎
24.1.1 Übungsaufgaben
Aufgabe: Datenraten verstehen
Informieren Sie sich im Internet über Maßeinheiten zur Angabe von Datenmengen und Datenraten wie MB oder Gbps.
Einige Firmen bieten Dienste an, die es erlauben, Daten online abzuspeichern und von überall mit einem Internetzugriff darauf zuzugreifen. Angenommen, eine solche Firma böte auch an, eine 1 TB Festplatte innerhalb von 24h mit einem Kurierdienst zuzustellen. Welche Datenrate müsste ein Internetzugriff mindestens bereitstellen, um die gleiche Datenmenge in der selben Zeit herunter zu laden?
Angenommen eine solche Firma verwendet zum Speichern der Nutzerdaten Container mit jeweils 2000 Servern mit jeweils 500 GB Speicherkapazität. Welcher Datenrate entspricht der 10-stündige Transport eines solchen Containers mit einem Lastwagen von einem Datenzentrum zu einem anderen?
Aufgabe: Prüfbits programmieren
Schreiben Sie eine python Funktion add_checksum(s), die einer gegebenen
Zeichenkette, die nur Nullen und Einsen enthält, eine Null oder eine
Eins anhängt, je nachdem, ob die urpsrüngliche Anzahl der Einsen
gerade oder ungerade ist. Der Rückgabewert der Funktion soll also eine
entsprechend um ein Zeichen längere Zeichenkette sein.
Implementieren Sie außerdem eine Funktion is_valid(s), die eine
Zeichenkette aus Nullen und Einsen inklusive angehängter Prüfsumme auf
Übertragungsfehler untersucht. Wenn ein Übertragungsfehler
festegestellt wurde, soll die Funktion False zurück liefern,
ansonsten True.
Geben Sie verschiedene Beispielaufrufe an und zwar solche ohne Übertragungsfehler, solche mit erkanntem Übertragungsfehler und solche mit unerkanntem Übertragungsfehler.
Bonusaufgabe: Prüfbits variabler Länge programmieren
Mit \(n\) Bits können wir \(2^n\) verschiedene Werte darstellen; eine Prüfsumme der Länge \(n\) erlaubt es also (im Besten Fall), \(2^n - 1\) falsch übertragene Bits zu erkennen, wenn wir der übertragenen Nachricht die Binärdarstellung der Anzahl der Einsen modulo \(2^n\) anhängen.
Erweitern Sie die Funktionen aus der vorigen Aufgabe um einen
Parameter n, der die Länge der zu berechnenden Prüfsummen
angibt. Für n = 2 sollen also zwei Bits wie beschrieben
angehängt werden.
Geben Sie wieder Beispielaufrufe an, die:kumentieren, welche Übertragungsfehler erkannt werden und welche nicht.
Definieren Sie eine Funktion add_block_checksums(s,b,n), die in der
Zeichenkette s (aus Nullen und Einsen) hinter jedem Block der Länge
b eine Prüfsumme der Länge n einfügt. Falls die Länge von s kein
Vielfaches von b ist, sollen im letzten Block Nullen vor der
Prüfsumme angehängt werden. Definieren Sie außerdem eine Funktion
has_valid_blocks(s,b,n), die eine so verlängerte Zeichenkette auf
Übertragungsfehler überprüft.
Testen Sie Ihre Implementierung für b = 6 und n = 2 und
dokumentieren Sie welche Übertragungsfehler erkannt werden und welche
nicht.
Bonusaufgabe: Fehlerkorrektur programmieren
In einer vorigen Aufgabe haben Sie eine einfache Prüfsumme zur
Fehlererkennung in python implementiert. Ein einfaches Verfahren, Fehler
nicht nur zu erkennen sondern auch zu korrigieren, ist es jedes Bit
einer Nachricht dreimal hintereinander zu verschicken. Aus der
Nachricht 1011 wird also die Nachricht 111000111111. Falls
einzelne Bits in dieser Nachricht gekippt werden, kann die
ursprüngliche Nachricht trotzdem dekodiert werden, indem ein
Dreierblock von Bits immer dann in eine 1 zurück übersetzt wird,
wenn der Block mindestens zwei Einsen enthält.
Definieren Sie in python Funktionen encode und decode, die dieses
Verfahren implementieren. Testen Sie es für einige Eingaben und geben
Sie auch ein Beispiel an, bei dem die Rück-Übersetzung fehl schlägt.
24.2 Internet
Dieser Abschnitt liefert einen Überblick über Mechanismen und Protokolle der Vernetzungs-, Transport- und Anwendungsschicht, wie sie im Internet verwendet werden.
Die Vernetzungsschicht wird im Internet vom Internet Protocol (IP) implementiert. Die Aufgabe dieses Protokolls ist es, Datenaustausch über mehrere sogenannte Router zu ermöglichen, und wir werden die Grundideen des Routings sowie das zugrunde liegende Adressierungsschema der IP-Adressen skizzieren.
Auf der Transportschicht kommen im Internet das verbindungslose unzuverlässige User Datagram Protocol (UDP) und das verbindungsorientierte zuverlässige Transmission Control Protocol (TCP) zum Einsatz. Uns interessieren vor allem TCP und die Mechanismen, die zuverlässige Kommunikation über ein unzuverlässiges Netzwerk ermöglichen.
Schließlich skizzieren wir das Domain Name System (DNS) zur Namensauflösung im Internet, das Format und Mechanismen zum Austausch von Email, sowie das HyperText Transfer Protocol (HTTP) als Grundlage des World Wide Web (WWW).
Routing und IP-Adressen
Die Vernetzungsschicht implementiert im Internet einen unzuverlässigen Datenaustauschdienst auf Basis der Verbindungsschicht. Sie abstrahiert von dem Übertragungsverfahren und erlaubt es so, Daten unabhängig von der Netzwerktechnologie zu übertragen.
Im Internet werden Daten über sogenannte Router vom Absender zum Empfänger weiter geleitet. Damit das funktioniert, muss jeder Router im Internet wissen, über welchen seiner direkten Nachbarn welche anderen Rechner im Internet erreichbar sind. Dazu speichern Router eine sogenannte Routing-Tabelle, die eine Zuordnung von IP-Adressen oder Adressbereichen zu Netzwerkschnittstellen speichert, über die Daten an die entsprechende Adresse weitergeleitet werden sollen.
In Version 4 des Internet Protokolls bestehen Adressen aus 32 Bit, von
denen eine variable Anzahl Bits das Subnetzwerk und die restlichen
Bits einen Rechner1 in diesem Subnetzwerk spezifizieren. Die
Subnetze sind im Internet regional hierarchisch angeordnet, so dass
Router in einer Region der Welt nicht für jeden Rechner in einer
anderen Region einen Eintrag in der Routing-Tabelle abspeichern müssen
sondern nur einen Eintrag für alle Rechner im entsprechenden
Subnetz. IP-Adressen werden als durch Punkte getrennte Dezimalzahlen
notiert. Der Webserver der Uni-Kiel hat zum Beispiel die Adresse
134.245.13.21.
Es gibt verschiedene Verfahren, Routing-Tabellen in Routern eines Netzwerkes zu verwalten.
In Netzwerken aus wenigen Rechnern können Routing-Tabellen von einem Administrator festgelegt und auf allen Routern verteilt werden. Dieses sogenannte statische Routing ist jedoch unflexibel, da bei Änderungen der Netzwerktopologie (zum Beispiel durch Hinzufügen oder Ausfall eines Routers) die Routing-Tabellen auf allen Routern von Hand aktualisiert werden müssen.
Ein verteilter Mechanismus zur Verwaltung der Routing-Tabellen ist das sogenannte Distance Vector Routing. Dabei speichern Router in ihren Tabellen nicht nur über welche Schnittstelle andere Rechner erreichbar sind sondern nauch zu welchen Kosten. Die Kosten können dabei als Anzahl der Zwischenstationen, als Verzögerungszeit oder abhängig vom Durchsatz der Verbindung definiert werden. In regelmäßigen Abständen oder bei Änderungen der Netzwerktopologie, sendet ein Router einen sogenannten Distance Vector an alle seine Nachbarn, der beschreibt, welche Rechner er mit welchen Kosten erreichen kann.
Ein Router, der neu ins Netz kommt, kennt noch keine anderen Rechner und sendet als erstes einen Distance Vector, der nur ihn selbst mit den Kosten 0 enthält, an alle seine Nachbarn. Diese senden daraufhin ihre eigenen Distanzvektoren, mit deren Hilfe der neue Router dann seine Routing-Tabelle erweitern kann. Auf diese Weise halten alle beteiligten Rechner ihre Routing-Tabellen automatisch auf aktuellem Stand. Ausfallende Rechner können erkannt werden, indem jedem Eintrag in der Routing-Tabelle ein Zeitstempel hinzugefügt wird. Sobald eine Route eine bestimmte Zeit nicht mehr aktualisiert wird, wird angenommen, dass sie nicht mehr existiert. In diesem Fall werden im nächsten Distanzvektor für den entsprechenden Eintrag die Kosten “unendlich” propagiert.
Ein alternatives Verfahren ist sogenanntes link state routing, bei dem jeder Router die gesamte Topologie des Netzwerkes lernt und daraus eigenständig kürzeste Wege berechnen kann. Dazu senden alle Router in regelmäßigen Abständen die Kosten der Verbindungen zu ihren direkten Nachbarn an alle Nachbarn. Diese Information wird von allen Routern weitergeleitet, so dass das Netzwerk mit allen solchen Nachrichten von allen Routern geflutet wird. Dadurch lernen alle Router die Kosten aller direkten Verbindungen und können daraus Gesamtkosten für zusammengesetzte Pfade ausrechnen. Ausfallende Router werden dadurch erkannt, dass ihre direkten Verbindungen zunächst noch von ihren Nachbarn aber nicht mehr von ihnen selbst propagiert werden.
Das Internet Protokoll umfasst unterschiedliche Routing-Verfahren die auf unterschiedlichen Hierarchiestufen angewendet werden und die hier skizzierten Mechanismen verfeinern oder kombinieren.
Zuverlässige Kommunikation über ein unzuverlässiges Netzwerk
Im Internet gibt es zwei gängige Protokolle auf der Transportschicht.
Das User Datagram Protokoll (UDP) ist wie das Internet Protokoll (IP), auf dem es basiert, verbindungslos und unzuverlässig. Daten können verloren gehen, dupliziert werden und in unterschiedlicher Reihenfolge ankommen. UDP stellt jedoch durch Prüfsummen sicher, dass korrumpierte Daten erkannt und verworfen werden. Außerdem ermöglicht es über sogenannte Ports die Kommunikation mit verschiedenen Prozessen über die selbe IP-Adresse. Während auf IP-Ebene Rechner über ihre IP-Adresse angesprochen werden, werden auf UDP-Ebene Prozesse auf Rechnern über eine IP-Adresse und einen Port angesprochen. Dadurch wird es möglich, dass viele verschiedene Anwendungen auf einem Rechner gleichzeitig auf das Internet zugreifen können. UDP wird vor allem von Anwendungen wie Internet-Telefonie verwendet, die auf kurze Verzögerungszeiten Wert legen und gelegentlichen Datenverlust verkraften können.
Das Transmission Control Protocol (TCP) stellt verbindungsorientierte zuverlässige Kommunikation auf Basis des Internet Protokolls bereit. Wie UDP verwendet es Ports, um verschiedene Prozesse auf einem Rechner zu identifizieren und Prüfsummen um korrumpierte Daten zu erkennen. Zwei über TCP verbundene Prozesse können miteinander in beide Richtungen beliebig große Datenmengen austauschen. Die Daten werden dazu von TCP in IP-Pakete verpackt, die separat verschickt werden.
Dadurch, dass Verbindungen im Internet heterogen (also insbesondere unterschiedlich schnell) sind, müssen Datenpakete von Routern in Puffern zwischengespeichert werden, bevor sie weiter verschickt werden können. Selbst über perfekte Verbindungen könnte also Datenverlust dadurch auftreten, dass der Puffer eines Routers voll ist und ankommende Pakete deshalb verworfen werden.
Um den Verlust von Paketen zu erkennen, erwartet der Absender bei TCP eine Empfangsbestätigung vom Empfänger. Falls diese nach Ablauf einer gewissen Zeit nicht eintrifft, nimmt der Absender an, dass das Paket verloren ging und sendet es erneut. Falls eine Empfangsbestätigung verloren geht, bekommt der Empfänger dadurch Pakete doppelt. Damit er diese als dupliziert erkennen kann, werden Pakete mit einer laufenden Nummer durchnummeriert. Bekommt ein Empfänger zweimal ein Paket mit der selben Nummer, kann er das zweite verwerfen.
Insbesondere bei einer Verbindung mit hohem Durchsatz und hoher Verzögerung ist es ineffizient, immer erst auf eine Bestätigung zu warten, bevor das nächste Paket losgeschickt wird. Bei sogenanntem Pipelining werden mehrere Pakete auf einmal losgeschickt, deren Bestätigungen später nacheinander eintreffen können. Der Empfänger kann die korrekte Reihenfolge der Pakete anhand der laufenden Nummer erkennen. Entweder verwirft er Pakete die außer der Reihe eintreffen, ohne sie zu bestätigen (dann werden sie später vom Absender erneut geschickt) oder er sortiert eintreffende Pakete in einem Empfangspuffer. TCP verwendet die letztere Variante mit einem Empfangspuffer. Außerdem werden Bestätigungen nicht einzeln verschickt sondern kumulativ: eine Bestätigung enthält dazu die nächste erwartete laufende Nummer. Bei Duplex-Kommunikation können Bestätigungen durch sogenanntes Piggybacking mit anderen Datenpaketen kombiniert werden.
Die Internet-Anwendungen DNS, Email und HTTP
IP-Adressen werden als Zahlenkombinationen notiert, die Menschen nur schwer auswendig lernen können. Das Domain Name System (DNS) ermöglicht eine Übersetzung hierarchisch strukturierter Klartextnamen in IP-Adressen auf Basis des User Datagram Protocols (UDP).
Domainnamen bestehen aus einem Hostnamen, möglicherweise mehreren
Subdomains, einer Domain und einer Top-Level Domain. Zum Beispiel ist
der Name www.uni-kiel.de zusammengesetzt aus dem Hostnamen www,
der Domain uni-kiel und der Top-Level Domain de.
Das DNS ist ein Internet-Dienst, der es erlaubt solche Namen in
zugehörige IP-Adressen zu übersetzen. Dazu muss jede Domain einen
Nameserver bereitstellen, der die IP-Adresse von in dieser Domain
erreichbaren Hosts kennt oder zumindest andere Nameserver für mögliche
Subdomains. Entsprechend gibt es zu jeder Top-Level Domain Nameserver,
die Nameserver für die in ihr verwalteten Domains kennen. Um die
IP-Adresse zu www.uni-kiel.de herauszufinden, könnten wir also
zuerst den Nameserver der Top-Level de Domain befragen. Dieser würde
uns einen Name-Server zur Domain uni-kiel nennen, den wir dann nach
der IP-Adresse des Hosts www fragen könnten.
Dieses Verfahren ist umständlich, da jeder Client mehrere Anfragen stellen und die aktuellen Adressen der Nameserver aller Top-Level Domains kennen müsste. Stattdessen können Clients sogenannte Name Resolver anfragen, die von Internet Service Providern (ISPs) zur Verfügung gestellt werden. Diese kennen die aktuellen Adressen aller Top-Level Domain Name Server und kombinieren mehrere Anfragen um die Anfrage eines Clients zu beantworten. Für häufig angefragte Domainnamen können Resolver auch Antworten zwischenspeichern, um sie nicht immer wieder neu erfragen zu müssen.
Das Domain Name System wird auch verwendet, um Emails vom Mailserver des Absenders zum Mailserver des Empfängers zu transportieren.
Beim Verschicken einer Email kommuniziert der Mailclient des Absenders per Simple Mail Transfer Protocol (SMTP) mit einem Mailserver und dieser dann mit dem Mailserver des Empfängers. Um Mails von seinem Mailserver herunterzuladen, kann der Empfänger das Post Office Protocol (POP) oder das Internet Message Access Protocol (IMAP) verwenden.
Eine Email besteht aus einem Header und einem Rumpf mit dem
eigentlichen Inhalt der Mail. Der Header enthält mindestens Felder
From für den Absender und einen Zeitstempel Date und in der Regel
auch ein Feld To für den Empfänger und eine Feld Subject für den
Betreff.
Der Message-Id Header identifiziert eine Email eindeutig. Dieser
Wert kann im In-Reply-To Feld verwendet werden um Konversationen
kenntlich zu machen. Der Received Header ermöglicht es,
nachzuvollziehen, welche Mailserver eine Email auf ihrem Weg zum
Empfänger weitergeleitet haben.
Ursprünglich wurde das Format für Emails nur für den Austausch von Textdaten im ASCII-Format konzipiert. Heutzutage können auch Emails in anderen Zeichensätzen (zum Beispiel chinesischen) verschickt werden. Auch Bild- und Tondateien können per Email verschickt werden. Dazu werden die Daten so umkodiert, dass existierende Mailserver, die davon ausgehen, dass die Nachrichten ASCII-Daten enthalten, weiter verwendet werden können.
Als letztes Anwendungsprotokoll im Internet streifen wir das HyperText Transfer Protocol (HTTP). Wie der Name sagt, ist es dazu da, sogenannte Hypertext Dokumente auszutauschen. Hypertext Dokumente enthalten Hyperlink genannte Referenzen auf andere Hypertext Dokumente und bilden so ein Netz von Dokumenten im Internet, das sogenannte World Wide Web (WWW). Hypertext Dokumente werden von Webservern bereitgestellt und von Webbrowsern heruntergeladen.
Hypertext Dokumente sind in der HyperText Markup Language (HTML)
verfasst, die wir später genauer kennen lernen werden. Sie werden über
sogenannte Universal Resource Locator (URL) adressiert, die im Fall
von Webseiten aus dem Zugriffsschema, einem Domainnamen und einem Pfad
bestehen. Der Identifier http://www.uni-kiel.de/index.html besteht
zum Beispiel aus der Protokollbezeichnung http:// als
Zugriffsschema, dem Domainnamen www.uni-kiel.de sowie dem Pfad
/index.html zum Zugriff auf eine entsprechende Datei auf dem
Webserver www der Domain uni-kiel.de.
URL’s können weitere Komponenten enthalten. Zum Beispiel kann dem Pfad
nach einem Fragezeichen ein sogenannter Querystring folgen und hinter
einer Raute # kann der Name eines Fragmentes einer Datei stehen.
-
In Wirklichkeit wird durch die IP-Adresse nicht ein Rechner sonder nein sogenannter Host spezifiziert, der mit seiner Netzwerkschnittstelle identifiziert wird. ↩︎
24.2.1 Übungsaufgaben
Aufgabe: Distance Vector Routing nachvollziehen
Betrachten Sie ein Netzwerk aus vier Routern, die im Quadrat verbunden sind, und beschreiben Sie, wie diese ihre Routing-Tabellen mit dem distance vector routing Verfahren aufbauen.
Angenommen, eine der Verbindungen wird getrennt. Beschreiben Sie, wie sich dadurch die Routing-Tabellen verändern.
Angenommen eine weitere Verbindung wird getrennt. Das Netz ist also nicht mehr zusammenhängend. Was passiert, wenn die Nachricht des Routers, der diese Veränderung als erstes propagiert, verloren geht?
Aufgabe: Email-Format verstehen und ausgeben
Schreiben Sie ein python-Programm, dass eine Email inklusive Headerdaten
im Terminal ausgibt. Geben Sie gültige Werte für die Header From,
To, Subject und Date an, nachdem sie sich im Internet über deren
Format informiert haben. Nach einer Leerzeile folgt dann der
eigentliche Inhalt der Email.
Alle Werte der Header und der Inhalt der Mail sollen vom Benutzer im
Terminal abgefragt werden, bevor die Email ausgegeben wird. Einen
Zeitstempel können Sie stattdessen mit datetime.now().isoformat() erzeugen,
wenn Sie ihr Programm wie folgt beginnen:
from datetime import datetime
24.3 Die HyperText Markup Language (HTML)
Eine der wichtigsten Anwendungen des Internet ist das WWW: ein weltweites Netz untereinander verlinkter sogenannter HyperText-Dokumente. Solche Dokumente werden mit Hilfe der Dokumentenbeschreibungs-Sprache HTML (für HyperText Markup Language) definiert, auf Webservern abgelegt und von Webbrowsern mit Hilfe des HyperText Transfer Protokolls (HTTP) von solchen herunter geladen.
HTML-Dokumente sind Textdokumente mit sogenanntem Markup: zusätzlichen Anweisungen zur Strukturierung. Die Struktur eines HTML-Dokuments wird durch sogenannte Tags spezifiziert, die das Dokument hierarchisch in seine Bestandteile zerlegen. Die Struktur eines einfachen HTML-Dokuments ist wie folgt.
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Dies ist eine HTML-Seite</title>
</head>
<body>
...
</body>
</html>
Die erste Zeile ist eine sogenannte Dokumenttyp-Definition, mit der
die verwendete HTML-Version kenntlich gemacht werden kann. Bei
Verwendung der aktuellen HMTL-Version genügt die hier gezeigt Angabe
<!DOCTYPE html>.
Das eigentliche HTML-Dokument ist in die Tags <html> und </html>
eingeschlossen. Tagnamen werden zwischen spitzen Klammern notiert. Das
erste Tag heißt öffnendes und das letzte schließendes Tag, wobei
schließende Tags stets den gleichen Namen haben wie zugehörige
öffnende Tags, diesem aber ein Schrägstrich vorangestellt wird. Durch
öffnende Tags begonnene Bereiche müssen in der Regel durch ein
schließendes Tag beendet werden.1 Dabei muss die hierarchische
Struktur des Dokumentes abgebildet werden.
Ein HMTL-Dokument hat zwei Bestandteile: einen Kopf (abgesetzt durch
<head> und </head>) und einem Rumpf (abgesetzt durch <body> und
</body>). Hier wäre es falsch, das schließende </head>-Tag nach
dem öffnenden <body>-Tag zu notieren, da dies nicht der
hierarchischen Struktur des Dokumentes entsprechen würde. Der Kopf
enthält Meta-Informationen, wie hier den Zeichensatz und den Titel des
Dokumentes, die nicht angezeigt werden.2 Der Rumpf enthält den
eigentlichen Inhalt des Dokumentes, der im Browser angezeigt wird. Im
folgenden behandeln wir Tags zur Strukturierung des Rumpfes eines
HTML-Dokuments.
Überschriften werden durch Tags mit den Namen h1 bis h6 (h
für heading) deklariert. h1 bezeichnet dabei eine Überschrift erster
Ordnung, h2 eine zweiter Ordnung und so weiter. In Browsern werden
Überschriften erster Ordnung in der Regel am größten und fett
dargestellt, Überschriften zweiter Ordnung etwas kleiner und so
weiter. Die Darstellung von Dokumentbestandteilen ist jedoch explizit
nicht in HTML spezifiziert. HTML beschreibt nur die Struktur von
Dokumenten. Wie ein Dokument dargestellt werden soll, kann jedoch
gesondert mit CSS (für Cascading Style Sheets) beschrieben werden, wie
wir später noch sehen werden.
Absätze werden durch Tags mit dem Namen p (für paragraph)
begrenzt. In Browsern werden Absätze in der Regel abgesetzt notiert
und zwar unabhängig davon, wie sie in der HTML-Datei selbst formatiert
beziehungsweise umgebrochen sind. Zur Anzeige eines HTML-Dokumentes im
Browser ist nur die durch Tags deklarierte Struktur relevant nicht
jedoch die Formatierung anhand von Zeilenumbrüchen in der HTML-Datei
selbst. Bereiche, die genauso wie im Quelltext der HTML-Datei
umgebrochen werden sollen, können zwischen Tags mit dem Namen pre
(für pre-formatted text) deklariert werden. Dies ist zum Beispiel
nützlich, um Programmtext in HTML-Dokumenten anzuzeigen.
Die wichtigsten Bestandteile von HTML-Dokumenten im Vergleich zu
gewöhnlichen Dokumenten sind Verknüpfungen zu anderen
Dokumenten. Diese werden durch Tags mit dem Namen a (für anchor)
deklariert. Anders als bei den bisher vorgestellten Tags, bestehen
Verknüpfungen aus einem angezeigten Teil (dem Verknüpfungstext) und
einem nicht angezeigten Teil (dem Verknüpfungßziel). Der
Verknüpfungstext wird wie gewohnt zwischen den Tags geschrieben. Das
Verknüpfungsziel wird als sogenanntes Attribut des öffnenden Tags mit
dem Namen href (für Hyper Reference) notiert. Zum Beispiel
Beschreibt <a href="http://www.uni-kiel.de">Uni Kiel</a> eine
Verknüpfung mit dem Text Uni Kiel und dem Ziel
http://www.uni-kiel.de. Verknüpfungsziele werden also durch ihren
URI spezifiziert. Statt einen vollständigen URI als Verknüpfungsziel
anzugeben, kann der Domainname auch weggelassen werden, um ein
Dokument der selben Domain zu verlinken. Analog zu Dateisystemen kann
auch ein relativer Pfad angegeben werden, der dann ausgehend vom
Verzeichnis des aktuellen Dokumentes interpretiert wird.
Tags mit dem Namen a werden nicht nur für Verknüpfungen sondern auch
zur Markierung von Bestandteilen des Dokuments verwendet, auf die
durch Angabe des Anker-Namens nach # explizit verlinkt werden
kann. Mit <a name="Hauptteil">...</a> wird ein sogenannter Anker zu
dem umfassten Bestandteil des Dokuments deklariert. Wikipedia
deklariert Anker für die Bestandteile aller Dokumente. Wir können also
zum Beispiel durch <a href="http://de.wikipedia.org/wiki/Hypertext_Markup_Language#HTML-Struktur">HTML-Struktur</a>
direkt auf den Abschnitt “HTML-Struktur” des Wikipedia-Eintrags zu
HTML verlinken. In Browsern werden Verknüpfungen in der Regel in einer
anderen Farbe und unterstrichen dargestellt um sie von normalem Text
abzusetzen. Obwohl CSS es erlaubt die Darstellung nach Belieben
anzupassen, sollte mit solchen, von vielen internalisierten,
Konventionen nicht (oder nur aus sehr guten Gründen) gebrochen werden.
Bilder können in HTML-Dokumente eingebunden werden, indem ihr URI
als Attribut src eines Tags mit dem Namen img angegeben wird. Zum
Beispiel können wir durch <img src="http://www.uni-kiel.de/home/grafik/kopf-cau-block.gif"> das Logo
der Uni-Kiel in ein HTML-Dokument einbinden.3 Da Bei
Bildern kein eigentlicher Inhalt notiert wird, kann das schließende
Tag entfallen. Alternativ können wir auch durch einen angehängten
Schrägstrich wie in <img src="..." /> anzeigen, dass das gerade
geöffnete Tag direkt wieder geschlossen wird.
Aufzählungslisten werden in HTML durch Tags mit den Namen ol
(für ordered list) beziehungsweise ul (für unordered list)
deklariert. Geordnete Listen werden durchnummeriert während in
ungeordneten Listen die Einträge durch ein sogenanntes Bullet (zum
Beispiel einen kleinen Kreis) kenntlich gemacht werden. Die Einträge
selbst werden zwischen Tags mit dem Namen li (für list item)
notiert. Zum Beispiel wird der folgende HTML-Code zur Deklaration
einer drei-elementigen ungeordneten Liste
<ul>
<li>erster Eintrag</li>
<li>zweiter Eintrag</li>
<li>dritter Eintrag</li>
</ul>
im Browser wie folgt dargestellt:
- erster Eintrag
- zweiter Eintrag
- dritter Eintrag
Tabellen werden durch Tags mit dem Namen table deklariert. Sie
bestehen aus Zeilen, die zwischen tr (für table row) geschrieben
werden und wiederum Einträge enthalten, die durch td (für table
data) kenntlich gemacht werden. Statt td kann auch th (für table
header) verwendet werden, um den Eintrag als Überschrift zu
kennzeichnen. Zum Beispiel könnte die folgende Tabelle
<table>
<tr>
<th>Vorname</th>
<th>Nachname</th>
<tr>
<tr>
<td>Sebastian</td>
<td>Fischer</td>
</tr>
<tr>
<td>Frank</td>
<td>Huch</td>
</tr>
<tr>
<td>Kai</td>
<td>Wollweber</td>
</tr>
</table>
im Browser wie folgt dargestellt werden:
| Vorname | Nachname |
|---|---|
| Sebastian | Fischer |
| Frank | Huch |
| Kai | Wollweber |
Die genaue Formatierung kann durch CSS beeinflusst werden.
Cascading Style Sheets (CSS)
Bei der Deklaration von HTML-Dokumenten wird zwischen deren Struktur (die in HMTL spezifiziert wird) und deren Formatierung unterschieden. Letztere wird in der Formatierungs-Sprache CSS (Cascading Style Sheets) deklariert. Style Sheets werden im Kopf einer HTML-Datei definiert und können auch in gesonderte Dateien ausgelagert werden um sie in mehreren HTML-Dateien wiederzuverwenden. Im folgenden werden beide Varianten:kumentiert.
<html>
<head>
<link rel="stylesheet" type="text/css" href="format.css">
<style type="text/css">
...
</style>
<head>
<body>
...
</body>
<html>
Hier werden zunächst mit Hilfe eines link-Tags ein externes Style
Sheet format.css eingebunden und dann zwischen Tags mit dem Namen
style weitere Formatierungsangaben gemacht.
Die Formatierungsangaben selbst haben das Format
Selektor {
Eigenschaft1: Wert1;
Eigenschaft2: Wert2;
...
}
wobei durch Selektor ein oder mehrer Bestandteile eines
HTML-Dokumentes ausgewählt werden können, die dann entsprechend der in
geschweifte Klammern eingeschlossenen Formatierungsanweisungen
dargestellt werden.
Zum Beispiel wird durch die folgende Angabe
h1 {
font-style: italics;
}
spezifiziert, dass Überschriften erster Ordnung kursiv dargestellt werden sollen. Es können auch mehrer Selektoren durch Kommata getrennt angegeben werden:
h1, h2, h3 {
font-style: italics;
}
Hier werden Überschriften erster bis dritter Ordnung kursiv dargestellt.
Selektoren können auch hierarchisch strukturiert werden. Zum Beispiel
bezieht sich der Selektor p ul auf alle ungeordneten Listen, die
innerhalb von Absätzen stehen. Um zu kennzeichnen, dass nur solche
Listen, die direkt innerhalb von Absätzen stehen, selektiert werden
sollen, können wir p>ul als Selektor verwenden. Um den Unterschied
der beiden Selektoren zu verdeutlichen betrachten wir den folgenden
Absatz einer möglichen HTML-Datei, der geschachtelte ungeordnete
Listen enhält.
<p>
<ul>
<li>
<ul>
<li>A.1</li>
<li>A.2</li>
</ul>
</li>
<li>B</li>
</ul>
</p>
Der Selektor p ul selektiert hier beide ungeordneten Listen, während
der Selektor p>ul nur die äußere selektiert, die direkt unterhalt
des Absatzes steht, nicht aber die innere, die innerhalb eines
Listeneintrags steht.
Nütliche Angaben zur Formatierung können Sie dem CSS-Kapitel der Seite SELFHMTL entnehmen. Nützlich sind zum Beispiel Angaben zu Rahmen in Tabellen:
table {
border-top: thin solid;
}
table, table th {
border-bottom: thin solid;
}
-
Eine Ausnahme dieser Regel ist das gezeigte
<meta>-Tag zur Angabe des Zeichensatzes. ↩︎ -
Der Titel einer HTML-Seite wird von gängigen Browsern in der Regel in der Titelzeile des Browserfensters angezeigt, aber nicht im angezeigten Dokument selbst. ↩︎
-
Bei der Anzeige fremder möglicherweise geschützter Bilder ist auf Grund von Copyright-Bestimmungen Vorsicht geboten. Bilder aus der Wikipedia dürfen unter bestimmten Vorraussetzungen verwendet werden. Bei Fragen konsultieren Sie bitte Ihren Anwalt. ↩︎
24.3.1 Übungsaufgaben
Aufgabe: Eigene HTML-Seite erstellen
Erstellen Sie mit einem Text-Editor eine eigene kleine Homepage im HTML-Format. Die Seite soll zumindest ein eigenes Foto, den eigenen Namen und eine Tabelle mit ein paar privaten Informationen enthalten. Außerdem soll sie auf mindestens drei ihrer Lieblings-Webseiten verweisen.
Aufgabe: HTML-Quelltext generieren
Erzeugen Sie eine Web-Seite, die eine Multiplikationstabelle für das kleine (oder gerne auch ein größeres) Ein-mal-Eins enthält, welche ungefähr wie folgt aussieht:
| 1 | 2 | 3 |
|---|---|---|
| 2 | 4 | 6 |
| 3 | 6 | 9 |
Ränder können Sie nach Geschmack hinzufügen oder weglassen.
Um unnötige Schreibarbeit zu sparen sollten Sie Ihre Programmierkenntnisse nutzen und die HTML-Tabelle mit Hilfe eines Python-Programms generieren. Die Ausgabe Ihres Programms können Sie anschließend in Ihre HTML-Seite per Copy-and-Paste einfügen.
24.4 Quellen und Lesetipps
24.5 Lösungen
Aufgabe: Datenraten verstehen
Die Einheit MB für Megabyte wird nicht einheitlich verwendet. Je nach Kontext beschreibt sie \(10^6 = 1000000\) oder \(2^{10} = 1048576\) Bytes (siehe Wikipedia). Im Netzwerkkontext und zur Angabe der Speicherkapazität von Festplatten beschreibt ein MB meist \(10^6\) Bytes, weshalb im Folgenden dieser Wert zu Grunde gelegt wird. Gbps steht für Gigabit pro Sekunde, misst also die Datenrate. 1 Gbps sind \(10^9\) Bits (nicht Bytes!) oder \(125\) MB pro Sekunde.
1 TB sind \(10^{12}\) Bytes oder \(8 \cdot 10^{12}\) Bits, 24 Stunden sind \(24 \cdot 60 \cdot 60\) Sekunden. Der Transport von 1 TB in 24 Stunden entspricht also einer Datenrate von \(8 \cdot 10^{12} / 24 \cdot 60 \cdot 60\) Bits pro Sekunde oder knapp 93 Mbps. Gängige DSL Anschlüsse bieten eine Datenrate von 16 Mbps, der WLAN Standard 802.11g bis zu 54 Mbps.
2000 Server mit jeweils 500 GB Speicherkapazität speichern zusammen \(10^6\) GB oder 1 Petabyte Daten. Bei einem Transport über zehn Stunden ergibt sich eine Datenrate von \(8 \cdot 10^{15} / 10 \cdot 60 \cdot 60\) Bits pro Sekunde, also gut 222 Gbps oder knapp ein vierzigstel der Datenrate eines im Jahr 2001 gelegten transatlantischen Glasfaserkabels.
Aufgabe: Prüfbits programmieren
Zur Berechnung von Prüfbits ist die folgende Hilfsfunktion nützlich, die zählt, wie viele Einsen eine Zeichenkette aus Nullen und Einsen enthält.
def count_ones(s):
count = 0
for i in range(0, len(s)):
if s[i] == '1':
count = count + 1
return count
Mit ihrer Hilfe können wir die Funktion add_checksum definieren,
indem wir ihr Ergebnis modulo zwei an die Eingabe anhängen.
def add_checksum(s):
return s + str(count_ones(s) % 2)
Zur Überprüfung verwenden wir ebenfalls count_ones, um zu testen, ob
die Anzahl der Einsen in der Eingabe gerade ist. Falls nicht, haben
wir einen Übertragungsfehler erkannt.
def is_valid(s):
return count_ones(s) % 2 == 0
Die folgenden Beispielaufrufe zeigen das Verhalten der definierten
Funktionen. Wenn der Funktion is_valid das Ergebnis von add_checksum
übergeben wird, liefert sie True zurück. Der zweite Aufruf von
valid ändert die Eingabe an einer Stelle, der dritte an zwei
Stellen. Die erste Änderung wird erkannt, die zweite nicht.
>>> add_checksum('101010')
'1010101'
>>> is_valid('1010101')
True
>>> is_valid('1010001')
False
>>> is_valid('1000001')
True
Bonusaufgabe: Prüfbits variabler Länge programmieren
Neben der in der vorherigen Aufgabe implementierten Hilfsfunktion
count_ones ist die folgende Funktion hilfreich, die die
Binärdarstellung einer natürlichen Zahl als Zeichenkette liefert.
def binary(n):
if n == 0:
return '0'
else:
bin = ''
while n > 0:
bin = str(n % 2) + bin
n = n // 2
return bin
Wir können nun die Prüfsumme berechnen, indem wir die Funktion
binary auf das Ergebnis von count_ones anwenden und gegebenenfalls
führende Nullen ergänzen.
def add_block_checksum(s,n):
checksum = binary(count_ones(s) % (2**n))
return s + ('0' * (n - len(checksum))) + checksum
Zur Überprüfung einer Prüfsumme können wir diese Funktion auf das Anfangsstück der Eingabe anwenden, das der ursprünglichen Nachricht entspricht und dann vergleichen, ob wir das selbe Ergebnis erhalten.
def is_valid_block(s,n):
message = s[0:len(s)-n]
return s == add_block_checksum(message,n)
Wir können bei \(n = 2\) bis zu drei Einsen in Nullen umwandeln und den so entstehenden Übertragungsfehler erkennen.
>>> add_block_checksum('10110100101',2)
'1011010010110'
>>> is_valid_block('1011010010110',2)
True
>>> is_valid_block('1001010010110',2)
False
>>> is_valid_block('1000010010110',2)
False
>>> is_valid_block('1000000010110',2)
False
>>> is_valid_block('1000000000110',2)
True
Im letzten Fall bleibt der Übertragungsfehler also unerkannt. Dies geschieht auch dann, wenn die Anzahl der Einsen gleich bleibt:
>>> is_valid_block('1111110000010',2)
True
Auch Übertragungsfehler in der Prüfsumme können unerkannt bleiben, wenn es zu ihr passende Übertragungsfehler in der Nachricht gibt:
>>> is_valid_block('1011011010111',2)
True
Hier wurde sowohl in der Prüfsumme als auch in der Nachricht eine Null in eine Eins umgewandelt, ohne dass dies erkannt wird.
Um blockweise Prüfsummen zu berechnen fügen wir der Nachricht zunächst
Nullen hinzu, wenn ihre Länge noch kein Vielfaches der Blockgröße
ist. Dann verwenden wir die Funktion add_block_checksum in einer Schleife
für jeden Block. Obwohl die Anzahl der Schleifendurchläufe vorab
bekannt ist, verwenden wir eine while-Schleife, um die Zählvariable
index in jedem Schritt um die Blockgröße b hochzuzählen.
def add_block_checksums(s,b,n):
mod = len(s) % b
if mod > 0:
s = s + ('0' * (b - mod))
index = 0
message = ''
while index < len(s):
message = message + add_block_checksum(s[index:index+b],n)
index = index + b
return message
Zur Überprüfung wenden wir is_valid_block in einer Schleife auf jeden Block
an und brechen ab, wenn wir einen Fehler gefunden haben.
def has_valid_blocks(s,b,n):
index = 0
valid = True
while valid and index < len(s):
valid = is_valid_block(s[index:index+b+n],n)
index = index + b + n
return valid
Es ist nun deutlich schwieriger durch zielloses Manipulieren einen unentdeckten Übertragungsfehler zu erzeugen.
>>> add_block_checksums('1100101100011011111011011',6,2)
'1100101111000111101111011011010010000001'
>>> has_valid_blocks('1100101111000111101111011011010010000001',6,2)
True
>>> has_valid_blocks('1100101111000111100011011011010010000001',6,2)
False
>>> has_valid_blocks('1100101111011111100011011011010010000001',6,2)
False
>>> has_valid_blocks('1100101111011111100011011011010010011101',6,2)
False
Bonusaufgabe: Fehlerkorrektur programmieren
Zur Implementierung von encode durchlaufen wir die Eingabe in einer
Zählschleife und fügen dabei der Ausgabe jedes Zeichen dreimal hinzu.
def encode(s):
code = ''
for i in range(0,len(s)):
code = code + s[i] * 3
return code
Zur Dekodierung verwenden wir die Funktion count_ones, die wir schon
zur Implementierung von Prüfsummen verwendet haben. Diesmal
durchlaufen wir die Eingabe in einer bedingten Schleife um die
Zählvariable in Dreierschritten hochzuzählen.
def decode(s):
msg = ''
index = 0
while index < len(s):
if count_ones(s[index:index+3]) >= 2:
msg = msg + '1'
else:
msg = msg + '0'
index = index + 3
return msg
Die folgenden Aufrufe zeigen das Kodieren sowie das Dekodieren mit keinem, einem oder zwei Übertragungsfehlern. Im letzten Fall schlägt die Fehlerkorrektur fehl, da zu viele Einsen im letzten Block in Nullen umgewandelt wurden.
>>> encode('101101')
'111000111111000111'
>>> decode('111000111111000111')
'101101'
>>> decode('111000111111000101')
'101101'
>>> decode('111000111111000001')
'101100'
Aufgabe: Distance Vector Routing nachvollziehen
Wir betrachten das folgende Netzwerk aus den Hosts A, B, C und D.
A --- B
| |
C --- D
Zu Beginn speichert jeder Host in seiner Routing-Tabelle nur eine Verbindung mit Kosten Null zu sich selbst.
Danach könnte zum Beispiel A seine Information an B und C schicken. Die Routing-Tabelle von B sähe danach wie folgt aus.
Ziel über Entfernung
------ ------ ------------
B B 0
A A 1
Angenommen, D schickt nun seine Tabelle an seine Nachbarn B und C. Dann wird die Tabelle von B wie folgt erweitert.
Ziel über Entfernung
------ ------ ------------
B B 0
A A 1
D D 1
Wenn B nun seinerseits diese Information an seine Nachbarn verschickt, kann A die folgende Tabelle aufbauen.
Ziel über Entfernung
------ ------ ------------
A A 0
B B 1
D B 2
Der Eintrag für A wird nicht übernommen, da schon ein kürzerer Weg bekannt ist. Sobald A eine Nachricht von C erhält, wird seine Tabelle wie folgt komplettiert.
Ziel über Entfernung
------ ------ ------------
A A 0
B B 1
D B 2
C C 1
Die anderen Hosts berechnen ihre Tabellen analog, zum Beispiel mit den folgenden Ergebnissen.
Ziel über Entfernung
------ ------ ------------
B B 0
A A 1
D D 1
C A 2
Ziel über Entfernung
------ ------ ------------
C C 0
A A 1
D D 1
B D 2
Ziel über Entfernung
------ ------ ------------
D D 0
A B 2
B B 1
C C 1
Angenommen, nun würde die Verbindung zwischen A und B getrennt. Diese beiden Hosts erhalten nun keine Nachrichten mehr voneinander, so dass sie sich nicht mehr als Nachbarn betrachten. Dadurch ändern sich mit der Zeit die Routing-Tabellen aller Hosts wie folgt.
Ziel über Entfernung
------ ------ ------------
A A 0
B C 3
D C 2
C C 1
Ziel über Entfernung
------ ------ ------------
B B 0
A D 3
D D 1
C D 2
Ziel über Entfernung
------ ------ ------------
C C 0
A A 1
D D 1
B D 2
Ziel über Entfernung
------ ------ ------------
D D 0
A C 2
B B 1
C C 1
Wird nun zum Beispiel auch noch die Verbindung zwischen A und C getrennt, ist A vom Rest des Netzwerkes abgeschnitten. Normalerweise merken das die anderen Hosts und entfernen entsprechene Routen aus ihrer Tabelle. Im ungünstigen Fall, dass zum Beispiel C die Nachricht von D bekommt, dass dieser A über zwei Hops erreichen kann, bevor C selbst die Nachricht verbreitet hat, dass es A nicht mehr erreicht, kann es jedoch zum sogenannten count to infinity problem kommen.
Dabei speichert C nun ab, dass es A über D mit Entfernung 3 erreichen kann, woraufhin D notiert, dass es A über C mit Entfernung 4 erreichen kann, woraufhin C notiert, dass es A über D mit Entfernung 5 erreichen kann und so weiter. Es gibt verschiedenen Mechanismen, dieses Problem zu vermeiden, die wir hier aber nicht weiter besprechen.
Aufgabe: Email-Format verstehen und ausgeben
from datetime import datetime
print("Wie ist Deine Adresse?")
frm = input()
print("An welche Adresse willst Du schicken?")
to = input()
print("Betreff?")
subject = input()
print("Nachricht eingeben (mit zwei Leerzeilen beenden):")
text = ""
blank = False
line = input()
while not blank or line != "":
text = text + line + "\n"
blank = line == ""
line = input()
print("From: <" + frm + ">")
print("To: <" + to + ">")
print("Subject: " + subject)
print("Date: " + datetime.now().isoformat())
print()
print()
print(text)
Aufgabe: HTML-Quelltext generieren
Das folgende python-Programm gibt eine Multiplikationstabelle für das kleine Einmaleins aus.
n = 10
print("<table>")
for i in range(0,n):
print(" <tr>")
for j in range(0,n):
print(" <td>" + str((i+1)*(j+1)) + "</td>")
print(" </tr>")
print("</table>")
Für n = 3 ergibt sich die folgende Ausgabe, die wir in eine
HMTL-Datei kopieren können, um die Tabelle im Browser anzusehen.
<table>
<tr>
<td>1</td>
<td>2</td>
<td>3</td>
</tr>
<tr>
<td>2</td>
<td>4</td>
<td>6</td>
</tr>
<tr>
<td>3</td>
<td>6</td>
<td>9</td>
</tr>
</table>
Sie wird in etwa wie folgt angezeigt.
| 1 | 2 | 3 |
|---|---|---|
| 2 | 4 | 6 |
| 3 | 6 | 9 |
25. Dynamische Webseiten
25.1 HTML-Formulare für Benutzereingaben
Neben den bisher vorgestellten Dokument-Elementen können in HTML-Dateien auch Eingabe-Elemente in Formularen definiert werden. Formulareingaben können, wie wir später sehen werden, mit Programmen auf dem Webserver oder auch mit Javascript im Webbrowser verarbeitet werden. Zunächst lernen wir jedoch kennen, wie Formulare definiert werden und welche die wichtigsten Eingabe-Elemente sind.
Ein Formular wird in HTML mit dem Tag form definiert. Innerhalb
des form-Tags dürfen beliebige andere HTML-Elemente stehen,
insbesondere auch Elemente für Benutzereingaben.
Das einfachste Element zur Eingabe ist ein Texteingabefeld, das
wir mit einem input-Tag definieren können, deren type-Attribut
den Wert "text" hat:
<form>
<input type="text" name="message">
</form>
Das Attribut name gibt an, unter welchem Namen der eingegebene Text
beim Absenden des Formulars übermittelt werden soll. Das input-Tag
hat keinen Inhalt und braucht kein schließendes Tag.
Zur Übermittlung der eingegebenen Daten fügen wir dem Formular einen
entsprechenden Knopf hinzu. Diesen können wir mit dem input-Tag und
dem Wert "submit" für das type-Attribut definieren.
<form>
<input type="text" name="message">
<input type="submit">
</form>
Beim Druck auf den Submit-Knopf wird die HTML-Seite neu geladen,
wobei die Formulareingaben der URL als sogenannter Query-Parameter
angehängt werden. Dieser wird der URL nach einem Fragezeichen
angehängt und könnte zum Beispiel ?message=Hallo lauten, wenn ein
Benutzer den Text Hallo in das Eingabefeld eingibt und dann auf den
Submit-Knopf drückt.
Bei komplexeren Formularen können strukturierende HTML-Elemente wie Tabellen verwendet werden, um die Eingabefelder anzuordnen.
Neben Texteingabefeldern können wir auch Auswahllisten definieren,
mit denen unter vorgegebenen Texten gewählt werden kann. Auswahllisten
werden mit dem Tag select definiert, wobei jede Option durch ein
option Tag angegeben wird. Die folgende Auswahlliste erlaubt zum
Beispiel die Angabe der Priorität einer Nachricht.
<select name="priority">
<option value="indifferent">egal</option>
<option value="important">wichtig</option>
<option value="urgent">dringend</option>
</select>
Das Attribut name definiert wieder den Namen, unter dem die gewählte
Option übermittelt wird. Die value-Attribute der option-Tags
werden als Wert der Eingabe mit dem gegebenen Namen priority
übermittelt, wenn die entsprechende Option vor Absenden des Formulars
ausgewählt wurde. Eine mögliche Eingabe bei Auswahl der letzten Option
wäre also priority=urgent.
Statt mit einer Auswahlliste können wir vorgegebene Eingaben auch mit
Hilfe sogenannter Radiobuttons definieren. Dieser werden als
input-Tags angegeben, deren type-Attribut den Wert "radio"
hat. Radiobuttons werden von Webbrowsern in der Regel als klickbare
Kreise dargestellt.
<ol>
<li>
<input type="radio" name="priority" value="indifferent"> egal
</li>
<li>
<input type="radio" name="priority" value="important"> wichtig
</li>
<li>
<input type="radio" name="priority" value="urgent"> dringend
</li>
</ol>
Hier verwenden wir eine geordnete Liste, um die Optionen anzuordnen. Da Radiobuttons von sich aus keinen anzuzeigenden Text enthalten fügen wir entsprechende Beschriftungen nach jedem Radiobutton ein. Alle Radiobuttons mit demselben Namen werden zu einer Gruppe von Optionen zusammengefasst, von denen nur höchstens eine ausgewählt werden kann. Die übermittelten Daten entsprechen hier also denen, die auch bei der vorherigen Auswahlliste übermittelt würden.
Schließlich können wir auch noch Checkboxen definieren, die als kleine Kästchen dargestellt werden, in denen Häkchen gesetzt werden können.
<input type="checkbox" name="confirmation">
Dieses Element definiert eine Checkbox, die, wenn ein entsprechendes
Häkchen gesetzt wird, beim Absenden des Formulars als
confirmation=on übermittelt wird.
Im folgenden Kapitel werden wir sehen, wie wir Formulareingaben aus den hier definierten Elementen mit Javascript im Browser verarbeiten können.
25.2 Client-seitige Webprogrammierung mit Javascript
Javascript ist eine Programmiersprache, die in einem Webbrowser
ausgeführt werden kann. Wir können Javascript-Programme ähnlich wie
Stylesheets in eine HTML-Datei einbinden: entweder direkt innerhalb
von script Tags im Header einer HTML-Datei oder durch Angabe der URL
einer Javascript-Datei.
Javascript-Code kann in HTML-Dateien in <script>-Tags eingebunden
werden und dabei entweder in die HTML-Datei selbst geschrieben werden
oder aus einer Datei mit der Endung .js geladen werden.
<script type="text/javascript" src="dateiname.js"></script>
Die Sprachelemente von Javascript sind die gewöhnlicher imperativer Programmiersprachen. Wir werden einige im Folgenden exemplarisch immer dann einführen, wenn wir sie benötigen.
Die folgende HTML-Datei verwendet Javascript, um dynamisch die URL, unter der sie erreichbar ist, anzuzeigen.
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>URL-Anzeige</title>
</head>
<body>
<script type="text/javascript">
document.write(window.location);
</script>
</body>
</html>
Die Methode document.write wird hier verwendet, um die in
window.location gespeicherte Zeichenkette in das Dokument
einzubauen.
Mit window.location.search kann auf den sogenannten query
parameter, also den Teil der URL ab dem Fragezeigen, zugegriffen
werden. In Kombination mit der Methode substring, die einen
Teilstring ab einer gegebenen Position selektiert, können wir den Teil
der URL hinter dem Fragezeichen mit
window.location.search.substring(1) abfragen.
Die folgende HTML-Datei wandelt diesen Teil der URL in eine Zahl um und fügt dann in einer Schleife Zahlen von der gegebenen Zahl abwärts zählend bis 1 in das Dokument ein.
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Countdown</title>
</head>
<body>
<script type="text/javascript">
var counter = parseInt(window.location.search.substring(1));
while (counter > 0) {
document.write("<p>" + counter + "</p>");
counter = counter - 1;
}
</script>
</body>
</html>
Hierzu verwenden wir eine while-Schleife, die in Javascript eine
etwas andere Syntax hat als in Python.
25.2.1 Übungsaufgaben
Aufgabe: Countdown mit Formular als Liste erzeugen
Wandeln Sie die Implementierung des Countdowns so ab, dass statt Absätzen eine ungeordnete Liste verwendet wird, um den Countdown darzustellen.
Erweitern Sie nun das Dokument derart, dass der Zähler in einem Formular von der Benutzerin eingegeben werden kann.
Bonus: Überlegen Sie, welche Eingabeelemente Sie für den Zähler verwenden können und definieren Sie Varianten der Seite für unterschiedliche Möglichkeiten.
25.3 Das Document Object Model (DOM)
Eine Besonderheit von Javascript sind bereitgestellte Objekte zum
Zugriff auf die Elemente eines HTML-Dokuments. Am Einfachsten kann auf
HTML-Elemente zugegriffen werden, wenn diese mit einem id Attribut
versehen werden. Zum Beispiel kann auf eine wie folgt definierte
ungeordnete Liste
<ul id="list"></ul>
in Javascript durch den Methodenaufruf
var list = document.getElementById("list");
zugegriffen werden. Das Ergebnis dieses Aufrufs ist ein Javascript-Objekt, das verwendet werden kann, um auf Eigenschaften der Liste zuzugreifen oder um diese zu manipulieren. Zum Beispiel können wir der Liste neue Items hinzufügen, wie wir später sehen werden.
Um mit Javascript auf die Elemente eines Dokumentes zugreifen zu
können, darf das Programm erst aufgerufen werden, wenn die Seite
komplett geladen ist. Dies können wir durch einen Eventhandler
erreichen, den wir dem body Tag wie folgt zuordnen können.
<body onload="processForm();">
...
</body>
Falls eine Javascript-Funktion processForm definiert ist, wird diese
aufgerufen, nachdem das Dokument geladen wurde.
Eine solche Funktion können wir wie folgt definieren.
function processForm() {
var query = window.location.search;
if (query != "") {
...
}
}
Hierdurch wird mit dem Schlüsselwort function eine Funktion mit dem
Namen processForm ohne Argumente definiert. Im Rumpf dieser Funktion
wird der Query-Parameter der URL mit Hilfe der Eigenschaft
window.location.search abgefragt und in der Variablen query
gespeichert. Eine bedingte Anweisung testet, ob der Query-String leer
ist. Falls nicht, wird der Rumpf der bedingten Anweisung ausgeführt,
in dem wir die Formulareingaben verarbeiten können.
Zur Verarbeitung der Formulareingaben benötigen wir einige Funktionen auf Zeichenketten, die wir im Folgenden exemplarisch einführen. Mit der folgenden Anweisung erzeugen wir aus dem Query-String eine Liste, die Formulareingaben enthält.
var params = query.substring(1).split("&");
Wenn zum Beispiel in der Variablen query die Zeichenkette "?message=Hallo&priority=urgent" gespeichert ist, hat die Liste params nach dieser Anweisung den Wert ["message=Hallo", "priority=urgent"].
Wir verwenden hier die Methode substring, die einen Teilstring ab der gegebenen Position selektiert. Da das erste Zeichen ? an Position Null steht, wird es durch diesen Aufruf abgeschnitten. Die Methode split zerlegt einen String anhand des gegebenen Trennzeichens, hier "&". Als Ergebnis wird eine Liste der Teilstrings zurückgegeben, die zwischen den Trennzeichen stehen.
Wir können nun die Liste params in einer Schleife durchlaufen und in jedem Schritt dem in der Variablen list gespeicherten HTML-Element
ein Item hinzufügen.
for (var i = 0; i < params.length; i = i+1) {
var item = document.createElement("li");
var text = document.createTextNode(params[i]);
item.appendChild(text);
list.appendChild(item);
}
Hier verwenden wir eine for-Schleife, die sich deutlich von einer Zählschleife in Python unterscheidet. Der Kopf der for-Schleife definiert eine Variable i, die alle Indizes der Liste params durchläuft. Die beiden ersten Zeilen des Schleifenrumpfes verwenden Methoden zum Erzeugen von HTML-Elementen und Text-Knoten. In der Variablen item wird ein neu erzeugtes li Element gespeichert, die Variable text speichert einen neuen Text-Knoten mit dem aktuellen
Name-Wert-Paar der Formulareingabe.
Die beiden letzten Zeilen des Schleifenrumpfes verwenden die Methode appendChild, um das neu erzeugte List-Item der in der Variablen list gespeicherten Liste hinzuzufügen.
Wenn wir nach Definition der Funktion processForm das definierte Formular ausfüllen und absenden werden daraufhin der in der selben Seite enthaltenen Liste die Formulareingaben hinzugefügt.
25.3.1 Übungsaufgaben
Aufgabe: Multiplikationstabelle mit DOM erzeugen
In dieser Aufgabe sollen Sie eine HTML-Seite schreiben, die mit Hilfe des DOM von Javascript eine Multiplikationstabelle einzugebender Größe erzeugt. Eine Multiplikationstabelle der Größe 3 könnte zum Beispiel so aussehen:
1 2 3
2 4 6
3 6 9
Definieren Sie dazu zunächst eine HTML-Datei, die ein Formular mit einem Texteingabefeld und einem Submit-Button zur Eingabe der Tabellengröße enthält. Außerdem soll die Seite eine leere Tabelle enthalten, die mit Hilfe des DOM von Javascript gefüllt werden soll.
Binden Sie dann in Ihre Seite ein Javascript-Programm aus einer
.js-Datei ein, das beim Laden der Datei ausgeführt wird. Falls im
Formular eine Tabellengröße eingegeben wurde, sollen in die leere
Tabelle entsprechende Einträge eingefügt werden, so dass eine
Multiplikationstabelle der gegebenen Größe entsteht.
Binden Sie dann in Ihre Seite eine CSS-Datei ein, die die Einträge mit Rahmen versieht und die eingetragenen Zahlen rechtsbündig ausrichtet.
Bonusaufgabe: Pythagoräische Tripel mit DOM erzeugen
Implementieren Sie eine HTML-Seite, die pythagoräische Tripel bis zu einer in einem Formular eingegebenen Größe mit Hilfe des DOM auflistet. Ein pythagoräisches Tripel besteht aus positiven ganzen Zahlen \(a < b < c\), die die Eigenschaft \(a^2 + b^2 = c^2\) erfüllen. Die im Formular eingegebene Größe soll als Obergrenze für die Variablen \(a,b,c\) verwendet werden.
Verwenden Sie das HTML-Tag sup zum Hochstellen von Text, um Ausgaben
der Form \(3^2 + 4^2 = 5^2\) zu erzeugen.
Definieren Sie sinnvolle Hilfsfunktionen, um Ihre Implementierung zu vereinfachen.
25.4 Lösungen
Aufgabe: Countdown mit Formular als Liste erzeugen
Die folgende HTML-Datei definiert ein Eingabefeld für eine Zahl. Sobald eine Zahl eingegeben und abgeschickt wurde, wird unter dem Eingabefeld ein Countdown angezeigt.
<!DOCTYPE html>
<html>
<head>
<title>Zähler</title>
<meta charset="utf-8" />
<link rel="stylesheet" type="text/css" href="styles.css">
</head>
<body>
<h1>Zähler</h1>
<form>
<input type="number" name="start">
<input type="submit">
</form>
<ul>
<script type="text/javascript">
var counter = parseInt(window.location.search.substring(7));
while (counter > 0) {
document.write("<li>");
document.write(counter);
document.write("</li>");
counter = counter - 1;
}
</script>
</ul>
</body>
</html>
Das Eingabefeld verwendet statt type="text" das Attribut type="number". Dies führt dazu, dass in einigen Browsern Pfeiltasten eingeblendet werden, mit denen die Zahl verändert werden kann.
Wenn die Eingabe abgeschickt wird, wird die Seite mit einem Query-String der Form ?start=42 neu aufgerufen. start ist hier der Name des Eingabefeldes für den Startwert und 42 ein möglicher eingegebener Wert. Die 42 erhalten wir also, indem wir den Query-String ab Position 7 in eine Zahl umwandeln.
Statt eines Absatzelementes erzeugen wir <li>-Elemente, die dem <ul>-Element hinzugefügt werden, in dem das Skript notiert ist.
Aufgabe: Multiplikationstabelle mit DOM erzeugen
Die folgende HTML-Datei definiert ein Eingabefeld für eine Zahl und eine Tabelle, in der die Multiplikationstabelle bis zur angegebenen Grenze erzeugt werden soll.
<!DOCTYPE html>
<html>
<head>
<title>Multiplikationstabelle</title>
<script src="multtab.js"></script>
<link rel="stylesheet" href="multtab.css">
</head>
<body onload="fillMultTab();">
<form>
<input type="number" name="size">
<input type="submit" value="los">
</form>
<table id="multtab"></table>
</body>
</html>
Nachdem das Dokument geladen ist, wird die Funktion fillMultTab aufgerufen, die in der Datei multtab.js definiert ist, die ihrerseits im Kopf des Dokumentes geladen wurde.
function fillMultTab() {
var query = window.location.search;
if (query.length > 0) {
var tab = document.getElementById('multtab');
var size = parseInt(query.substring(6));
for (var rowIndex = 1; rowIndex <= size; rowIndex = rowIndex + 1) {
var row = document.createElement('tr');
for (var colIndex = 1; colIndex <= size; colIndex = colIndex + 1) {
var col = document.createElement('td');
var prod = document.createTextNode(rowIndex * colIndex);
col.appendChild(prod);
row.appendChild(col);
}
tab.appendChild(row);
}
}
}
Diese Funktion greift auf das Tabellen-Objekt anhand des Wertes seines id-Attributes zu. Die eingegebene Zahl wird aus dem Query-String extrahiert, falls eine Zahl eingegeben wurde.
In einer Schleife werden dann zunächst Tabellenzeilen erzeugt und der Tabelle hinzugefügt und dann in einer geschachtelten Schleife jeder erzeugten Zeile die einzutragenden Produkte hinzugefügt. Elemente mit Kindern erzeugen wir mit Hilfe der Methode createElement, Text-Objekte mit createTextNode. Beide Schleifen laufen von 1 bis zur eingegebenen Zahl, so dass eine quadratische Tabelle ausgegeben wird.
Damit die Zahlen rechtsbündig ausgerichtet werden, fügen wir der eingebundenen Datei multtab.css die folgende Definition hinzu.
td {
border: thin solid grey;
text-align: right;
width: 2em;
}
tr:first-child, td:first-child {
font-weight: bold;
}
Zusätzlich wird hier die Breite von Tabellenzellen vereinheitlicht und jeder Eintrag mit einem grauen Rahmen versehen. Außerdem werden Einträge der ersten Zeile sowie der ersten Spalte fett dargestellt.
Bonusaufgabe: Pythagoräische Tripel mit DOM erzeugen
Das folgende HTML-Dokument erzeugt eine Auflistung pythagoräischer Tripel mit Hilfe des Document-Object Models in Javascript.
<!DOCTYPE html>
<html><head><meta charset="utf-8"><script>
function showPyTriples() {
var list = document.getElementById("pytriples");
var size = parseInt(window.location.search.substring(6));
var triples = pyTriples(size);
for (var index = 0; index < triples.length; index++) {
list.appendChild(pyTripleItem(triples[index]));
}
}
function pyTriples(size) {
triples = [];
for (var a = 1; a <= size; a++) {
for (var b = a; b <= size; b++) {
for (var c = b; c <= size; c++) {
if (a*a + b*b == c*c) {
triples.push({"a": a, "b": b, "c": c});
}
}
}
}
return triples;
}
function pyTripleItem(triple) {
return elem("li", [
text(triple["a"]), elem("sup", [text("2")]), text(" + "),
text(triple["b"]), elem("sup", [text("2")]), text(" = "),
text(triple["c"]), elem("sup", [text("2")])
]);
}
function elem(name, args) {
var result = document.createElement(name);
for (var i = 0; i < args.length; i++) {
result.appendChild(args[i]);
}
return result;
}
function text(value) {
return document.createTextNode(value);
}
</script></head><body onload="showPyTriples();">
<form>
Berechne Pythagoräische Tripel bis zu einer gegebenen Größe:
<input type="number" min="1" name="size" placeholder="Größe">
<input type="submit" value="anzeigen">
</form>
<ul id="pytriples"></ul>
</body></html>
Statt das Skript in einer Extradatei zu definieren und nach dem Laden des Dokumentes aufzurufen, schreiben wir es in die Datei hinein.
Das Skript definiert Hilfsfunktionen, die Dokument-Objekte erzeugen. Außerdem gibt es eine Funktion zum Erzeugen Pythagoräischer Tripel, die mit Hilfe geschachtelter Schleifen alle Pythagoräischen Tripel so aufzählt, dass der erste Summand kleiner als der zweite ist. Tripel werden von dieser Funktion als Liste von Hashes zurückgeliefert, die in Javascript Objects heißen.
26. Digitale Bildverarbeitung
26.1 Rastergrafiken und Histogramme
Rastergrafiken
Die Pixel einer Rastergrafik haben einen Farbwert, der in der Regel als Kombination aus Rot, Grün und Blau dargestellt wird. Ein Histogramm speichert zu jeder möglichen Intensität eines Farbwertes, wie viele Pixel mit dieser Intensität im Bild vorkommen. Unterschiedliche Histogramm-Typen unterscheiden sich dadurch, welcher Intensitätsbegriff zu Grunde elegt wird. Als Intensität kann zum Beispiel die Gesamt-Helligkeit eines Pixels definiert werden, die Helligkeit eines einzelnen Kanals (Rot, Grün oder Blau) oder auch eine Kombination daraus.
Im Folgenden betrachten wir Graustufen-Bilder, da mit ihnen bereits die grundlegenden Eigenschaften von Histogrammen demonstriert werden können.
Das Bildverarbeitungsprogramm GIMP bietet über den Menüpunkt Colors > Desaturate > Desaturate (Farben > Entsättigen > Entsättigen) die Möglichkeit, Bilder in Graustufen zu konvertieren. Dazu stehen unter anderem die Optionen Lightness (HSL) (Helligkeit (HSL)), Luminance (Leuchtkraft) und Average (HSI Intensity) (Durchschnitt) zur Verfügung, die sich darin unterscheiden, mit welcher Gewichtung die Farbinformation der einzelnen Farbkanäle zur Gesamthelligkeit kombiniert wird. Wir verwenden die Option Luminance (Leuchtkraft), die durch entsprechende Gewichtung berücksichtigt, dass der Grün-Anteil eines Pixels seine Helligkeit für das menschliche Auge stärker beeinflusst als Rot und Blau. Die Option Average (Durchschnitt (HSI Intensity)) gewichtet alle drei Farbkanäle gleich, während Lightness (HSL) (Helligkeit (HSL)) eine subjektive Helligkeit anhand eines komplizierteren Zusammenhangs berechnet als Luminance (Leuchtkraft).
Grauwert-Histogramme
Der Menüpunkt Fenster > Andockbare Dialoge > Histogramm öffnet einen Dialog, in dem das Histogramm eines Bildes angezeigt wird.
Helligkeit analysieren
Als erstes Beispiel betrachten wir ein dunkles Bild, das wir vorher in Graustufen umgewandelt haben.
| Bild mit überwiegend dunklen Pixeln | Histogramm des dunklen Bildes |
|---|---|
 |
 |
Das Histogramm dieses Bildes zeigt für jeden Grauwert zwischen 0 und 255, wie viele Pixel mit diesem Grauwert im Bild vorhanden sind. Auf der x-Achse sind dazu die Grauwerte aufgetragen und auf der y-Achse die entsprechende Anzahl von Pixeln.
Wir können erkennen, dass die meisten Pixel niedrige (also dunkle) Grauwerte haben, denn diesen ist eine deutlich größere Anzahl zugeordnet als den hohen (also hellen) Grauwerten.
Am linken Rand des Histogramms ist außerdem eine Häufung zu erkennen, die andeutet, dass das Bild leicht unterbelichtet ist, also dunkle Pixel, die in der Originalszene eigentlich unterschiedliche Intensitäten hatten, alle mit dem niedrigsten Grauwert (schwarz) dargestellt sind. Ebenso kann es in hellen Bildern auftreten, dass viele unterschiedlich helle Stellen mit dem höchsten Grauwert (weiß) dargestellt sind. In diesem Fall wäre das Bild überbelichtet. Spitzen an den Rändern des Histogramms sind im Fall von Fotos also ein Indikator für eine unpassende Belichtungszeit bei der Aufnahme.
Als zweites Beispiel betrachten wir nun ein helles Bild und sein Histogramm.
| Bild mit überwiegend hellen Pixeln | Histogramm des hellen Bildes |
|---|---|
 |
 |
Hier sind vor allem hohen (also hellen) Grauwerten eine große Anzahl von Pixeln zugeordnet.
Die Helligkeit eines Bildes lässt sich am Histogramm also daran erkennen, ob der Grauwert-Bereich mit hohen Pixelzahlen eher links oder eher rechts im Histogramm liegt.
Kontrast analysieren
Als Nächstes vergleichen wir die Histogramme von Bildern mit unterschiedlichem Kontrast. Dazu betrachten wir zunächst ein Bild mit hohem Kontrast, also eines in dem Pixel mit stark unterschiedlichen Graustufen häufig vorkommen.
| Bild mit hohem Kontrast | Histogramm des Bildes mit hohem Kontrast |
|---|---|
 |
 |
Das Histogramm dieses Bildes ist mittig ausgerichtet, das Bild hat also eine mittlere Helligkeit.
Um zu erkennen, wie wir anhand des Histogramms auf den Kontrast schließen können, vergleichen wir es mit dem Histogramm eines Bildes mit niedrigerem Kontrast.
| Bild mit niedrigem Kontrast | Histogramm des Bildes mit niedrigem Kontrast |
|---|---|
 |
 |
In diesem Bild kommen weniger unterschiedliche Pixel häufig vor. Im Histogramm ist der Grauwertbereich mit hoher Pixelzahl wieder mittig ausgerichtet, nun allerdings schmaler als im Bild mit hohem Kontrast.
Den Kontrast eines Bildes erkennen wir an seinem Histogramm also daran, ob sich die Grauwerte mit hoher Pixelzahl in einem schmalen Bereich konzentrieren oder weit über das Histogramm verteilt sind.
Pixel-weise Manipulation
Der Dialog Colors > Curves (Farben > Kurven) erlaubt, das Bild mit Hilfe sogenannter Kurven zu manipulieren. Diese Kurven bilden Grauwerte auf neue Grauwerte ab. Die y-Achse ist für die Kurven also wie die x-Achse von 0 bis 255 beschriftet.
Die einfachsten Kurven sind Geraden und wir untersuchen im Folgenden, wie wir mit Geraden die Helligkeit und den Kontrast von Bildern manipulieren können.
Helligkeit bearbeiten
Die einfachste Möglichkeit, um die Helligkeit eines Bildes zu beeinflussen, ist, zu jedem Grauwert eine Konstante zu addieren oder zu subtrahieren. Dies entspricht einer Verschiebung der Einheitsgeraden nach oben oder unten, wobei sie am Rand abgeschnitten wird, um im Zielbereich der Farbwerte zu bleiben. Diese Methode, ein Bild heller zu machen, führt also bei bereits hellen Bildern zu einer künstlichen Überbelichtung. Analog führt das Verdunkeln eines bereits dunklen Bildes zu künstlicher Unterbelichtung.
Das Histogramm wird mit dieser Methode nach rechts (oder links) verschoben, da die Pixelanzahlen gleich bleiben und nur anderen Grauwerten zugeordnet werden. Dabei kann der Grauwert-Bereich mit hohen Pixelanzahlen gegen den rechten (oder linken) Rand des Histogramms gedrückt werden, wodurch die künstliche Über- oder Unterbelichtung sichtbar wird.
Um diesen Effekt zu vermeiden, kann man beim Aufhellen eines Bildes dunkle Pixel stärker verändern als helle und beim Verdunkeln helle stärker als dunkle. Diese Methode aum Aufhellen kann durch eine Gerade umgesetzt werden, die durch den Punkt (255, 255) und ansonsten oberhalb der Identitätsgeraden verläuft. Analog erreicht man Verdunklung mit einer Geraden durch den Nullpunkt, die unterhalb der Identitätsgeraden verläuft.
Diese Methode verringert den Kontrast eines Bildes, da beim Aufhellen dunkle Grauwerte komplett entfernt werden. Ebenso kommen nach dem Verdunkeln ganz helle Grauwerte im Bild nicht mehr vor. Um diesen Effekt zu vermeiden, muss man Kurven verwenden, die sowohl durch den Nullpunkt als auch durch (255, 255) aber ansonsten oberhalb (oder unterhalb) der Identitätsgeraden verlaufen.
Kontrast bearbeiten
Um den Kontrast eines Bildes zu verändern brauchen wir Kurven, die sowohl oberhalb als auch unterhalb der Identitätsgeraden verlaufen. Zum Beispiel erhöht sich der Kontrast, indem dunkle Pixel dunkler und helle Pixel heller gemacht werden. Der Kontrast verringert sich hingegen, wenn dunkle Pixel heller und helle dunkler werden. Dies erreichen wir zum Beispiel durch eine Gerade durch den Punkt (128, 128) mit gegenüber der Identitätsgeraden erhöhter (bzw. erniedrigter) Steigung.
Im Histogramm äußert sich eine Erhöhung des Kontrasts dadurch, dass der Grauwert-Bereich mit hohen Pixelzahlen auseinandergezogen wird. Dabei kann er gegen den rechten und/oder linken Rand des Histogramms gedrückt werden, was zu künstlicher Über- und/oder Unterbelichtung führt. Dieser Effekt lässt sich vermeiden, indem Kurven gewählt werden, die durch die Eckpunkte gehen und ansonsten sowohl unter- als auch oberhalb der Identitätsgeraden verlaufen.
26.1.1 Übungsaufgaben
Aufgabe: Software zur Bildverarbeitung anwenden
Verändern Sie in GIMP (oder einem vergleichbaren Programm) die Helligkeit und den Kontrast verschiedener Bilder Ihrer Wahl mit Hilfe von Kurven. Beobachten Sie die Auswirkungen ihrer Anpassungen für verschiedenen Arten von Kurven. Speichern Sie die Ergebnisse und vergleichen Sie die Histogramme der unterschiedlich veränderten Bilder.
Aufgabe: Ziffern-Histogramm berechnen
Definieren Sie eine Python-Funktion digit_histogram,
die eine Liste aus beliebig vielen Ziffern (von 0 bis 9) als Argument erwartet
und ein Histogramm dieser Ziffern zurückliefert.
Das Ergebnis soll als Liste von zehn Zahlen dargestellt werden,
wobei jeweils am Index i die Anzahl der Vorkommen von i im Argument steht.
26.2 Bildverarbeitung in Python
Rastergrafiken in Python
Wir wollen nun Python-Funktionen schreiben, mit denen Histogramme
berechnet und Bilder manipuliert werden können. Dazu verwenden wir das
Paket pillow, das einen einfachen Zugriff auf Bilder in verschiedenen
Dateiformaten implementiert.
Nach der Installation über die Paketverwaltung können wir das Paket mit
from PIL import Image
in eigene Python-Programme einbinden. Danach können wir über das
Modul Image Funktionen und Klassen zum Zugriff auf Bilder verwenden.
Die Klasse Image dieses Moduls repräsentiert ein Bild.
Neue Objekte der Klasse Image können wir erzeugen, indem wir sie
mit der Funktion Image.open aus einer Datei einlesen.
image = Image.open('filename.png')
Alternativ können wir ein Bild mit der Kontruktor-Funktion Image.new durch Angabe seiner Größe und eines
Farbwertes erzeugen, der für alle Pixel verwendet wird.
image = Image.new('RGB', (width, height), (255, 255, 255))
Der erste Parameter ist ein String, der das Farbformat des neuen Bildes angibt:
'RGB' für ein RGB-Farbbild oder 'L' für ein Grauwertbild (“L” steht hier
für luminosity, also Helligkeit).
Schließlich können wir Bilder auch abspeichern, indem wir die Methode
save verwenden.
image.save('filename.png')
Objekte dieser Klasse haben Attribute width und height zum
Zugriff auf ihre Größe. Außerdem ist es möglich mit
color = image.getpixel((x, y))
auf den Farbwert des Pixels an Position (x, y) zuzugreifen und diesen
mit
image.putpixel((x, y), color)
zu verändern, wenn image ein Image-Objekt ist. Die Pixelkoordinaten werden hierbei als Paar in runden Klammern angegeben. Paare sind (wie Tripel und größere Tupel) in Python Datenstrukturen, auf die ähnlich wie auf Listen zugegriffen werden kann, die aber nicht mutierbar sind.
Für Grauwertbilder sind die Farbwerte einfache Zahlen von 0 bis 255, die Graustufen angeben. Für Farbbilder sind die Farbwerte dagegen Tripel aus Zahlen, jeweils von 0 bis 255, die Rot-, Grün- und Blauwerte der Farbe. Wir können also
white = (255, 255, 255)
schreiben, um einen weißen Farbwert zu erzeugen. Ist color ein
Farbwert, so speichern die folgenden Zuweisungen den Rot-, Grün- bzw.
Blau-Wert (zwischen 0 und 255) des Farbbildes image an der Position
(x, y) in einer entsprechenden Variablen.
red = image.getpixel((x, y))[0]
green = image.getpixel((x, y))[1]
blue = image.getpixel((x, y))[2]
Als erstes Beispiel für Bildverarbeitung in Python definieren wir eine Prozedur zur Umwandlung eines übergebenen RGB-Bildes in Graustufen.
def desaturate(image):
for y in range(0,image.height):
for x in range(0,image.width):
gray = average(image.getpixel((x, y)))
image.putpixel((x, y), (gray, gray, gray))
Sie durchläuft alle Pixel des Bildes, berechnet den Grauwert mit Hilfe
einer noch zu definierenden Funktion average und überschreibt dann
den aktuellen Pixel mit seinem Grauwert. Die Funktion average
berechnet zunächst die Rot-, Grün- und Blauwerte des übergebenen
Farbwerts (das Tupel color mit drei Werten) und gibt dann deren Mittelwert zurück.
def average(color):
return round((color[0] + color[1] + color[2]) // 3)
Die folgende Prozedur liest ein Bild aus einer Datei ein, wandelt es in Graustufen um und speichert es mit einem anderen Namen ab.
def save_desaturated(base_name):
image = Image.open(base_name + '.png')
desaturate(image)
image.save(base_name + '_gray.png')
Dazu wird der Teil des Dateinamens vor der Dateiendung .png
übergeben. Wenn die eingelesene Datei den Namen filename.png hat,
muss also 'filename' übergeben werden. Das Graustufenbild wird dann
in einer Datei mit dem Namen filename_gray.png abgespeichert.
Grauwert-Histogramme
Als Nächstes definieren eine Funktion zur Berechnung eines Histogramms der Grauwerte eines Bildes.
def gray_histogram(image):
histogram = [0] * 256
for y in range(0,image.height):
for x in range(0,image.width):
gray = average(image.getpixel((x, y)))
histogram[gray] = histogram[gray] + 1
return histogram
Dazu erzeugen wir eine Liste aus 256 Zahlen, einer für jeden Grauwert. Diese Liste füllen wir dann, indem wir alle Pixel durchlaufen, den Grauwert jedes Pixels berechnen und jedesmal die entsprechende Anzahl erhöhen.
Helligkeit analysieren
Aus dem Histogramm lassen sich, ohne Kenntnis des Bildes, interessante Eigenschaften berechnen. Als Beispiel definieren wir eine Funktion, die die mittlere Helligkeit eines Bildes nur anhand seines Histogramms berechnet. Dazu berechnen wir gleichzeitig die Anzahl der Pixel und die Summe der Grauwerte aller Pixel. Letztere berechnen wir, indem wir jeden Grauwert mit der Anzahl der Pixel mit diesem Grauwert multiplizieren und die Ergebnisse addieren.
def mean_brightness(histogram):
total_gray = 0
pixel_count = 0
for gray in range(0,256):
count = histogram[gray]
total_gray = total_gray + gray * count
pixel_count = pixel_count + count
return round(total_gray / pixel_count)
Für das dunkle Bild vom Anfang dieses Abschnitts ergibt sich eine mittlere Helligkeit von 63, für das helle Bild eine von 189.
Pixel-weise Manipulation
Zur Manipulation von Bildern in Graustufen können wir, wie in GIMP gesehen, Abbildungen von Grauwerten in Grauwerte verwenden. Diese stellen wir in Python als Listen der Länge 256 dar, deren Einträge Zahlen zwischen 0 und 255 sind. So dargestellte Abbildungen können wir mit der folgenden Prozedur auf Bilder anwenden.
def change_pixels(image, gray_map):
for y in range(image.height):
for x in range(image.width):
gray = gray_map[average(image.getpixel((x, y)))]
image.putpixel((x, y), (gray, gray, gray))
Diese Prozedur durchläuft alle Pixel, berechnet den neuen Grauwert anhand des alten Grauwertes und der übergebenen Abbildung und überschreibt den alten Grauwert durch den neuen.
Helligkeit bearbeiten
Als Beispiel für eine Abbildung von Grauwerten berechnen wir eine Abbildung zum Aufhellen (oder Verdunkeln) eines Bildes durch Addition (oder Subtraktion) einer Konstanten.
def brightness_adjustment(diff):
gray_map = [0] * 256
for gray in range(0,256):
new_gray = gray + diff
new_gray = max(0, new_gray)
new_gray = min(new_gray, 255)
gray_map[gray] = new_gray
return gray_map
Diese Funktion erzeugt eine Abbildung als Liste und weist dann jedem Grauwert den Grauwert zu, auf den er abgebildet werden soll. Dazu wird die übergebene Konstante auf den aktuellen Grauwert addiert. Subtraktionen werden durch negative Parameter erreicht. Bevor ein Grauwert gespeichert wird, wird er durch Vergleich mit 0 und 255 auf den Zahlenbereich für Grauwerte eingeschränkt.
Die Prozedur save_with_new_brightness ändert die mittlere Helligkeit eines mit dem gegebenen Namen gespeicherten Bildes auf den übergebenen Wert und speichert es unter einem neuen Namen ab.
def save_with_new_brightness(base_name, new_mean):
image = Image.open(base_name + '.png')
gray_hist = gray_histogram(image)
old_mean = mean_brightness(gray_hist)
gray_map = brightness_adjustment(new_mean - old_mean)
change_pixels(image, gray_map)
image.save(base_name + '_luma' + str(new_mean) + '.png')
Die Prozedur berechnet zunächst ein Histogram und daraus dann die mittlere Helligkeit des Bildes. Aus der Differenz der aktuellen und der übergebenen Helligkeit wird eine Abbildung von Grauwerten berechnet, die die Helligkeit entsprechend anpasst. Diese wird schließlich auf das eingelesene Bild angewendet, bevor es unter einem neuen Namen gespeichert wird.
Auf ähnliche Weise können wir beliebige Abbildungen von Grauwerten berechnen und zur Manipulation von Bildern auf diese anwenden. Zum Beispiel könnten wir die Helligkeit mit Hilfe von Geraden durch einen Eckpunkt verändern oder sogar beliebige Funktionen als gray_map darstellen.
26.2.1 Übungsaufgaben
Aufgabe: Grauwerte berechnen
Definieren Sie eine Python-Funktion luminosity, die einen gewichteten Mittelwert der Farbkanäle einer übergebenen Farbe zurückgibt. Rot soll dabei 30% ausmachen, Grün 59% und Blau 11%.
Aufgabe: Histogramm zeichnen
Definieren Sie eine Funktion render_histogram, die als Eingabe ein
Histogramm erwartet und ein Image-Objekt zurück liefert. Das
erzeugte Bild soll 256 mal 256 Pixel groß sein und die Anzahl der
Pixel zu jeder Intensität ähnlich wie GIMP darstellen. Überlegen Sie,
wie sie das Bild in Abhängigkeit der größten vorkommenden Anzahl so
skalieren, dass diese genau an den oberen Rand stößt.
Hinweis: Die Funktion max liefert das größte im Aufruf übergebene Argument zurück. Wenn ihr als einziges Argument eine Liste übergeben wird, liefert sie das größte Element der Liste zurück.
Aufgabe: Kontrastveränderung programmieren
Definieren Sie eine Funktion contrast_adjustment, die den Kontrast eines Bildes mit Hilfe einer Geraden durch den Punkt (128,128) anpasst. Die Steigung der Geraden soll als Parameter übergeben werden, der Rückgabewert der Funktion soll eine als Liste dargestellte gray_map, also eine Abbildung von Grauwerten in Grauwerte sein.
Aufgabe: Andere Graustufen-Abbildungen
Definieren Sie Listen - Funktionen (Grauwert -> Grauwert), die folgende Abbildungen erzielen:
- Invertierung (Erzeugung eines Negativbildes)
- Aufhellen oder Abdunkeln, ohne Überbelichtungs- bzw.Unterbelichtungseffekt
- Partielle Kontrasterhöhung in einem Helligkeitsbereich, z. B. Aufhellen der Schatten oder Abdunkeln der Spitzlichter
Bonusaufgaben
Schreiben Sie Programme, die folgende Ideen umsetzen:
- Detektion und farbige Markierung von über- und unterbelichteten Bereichen
- Colorierung eines Graustufenbildes
- Änderung der Auflösung eines Bildes
- Spiegelung (Drehung) eines Bildes
- Objekterkennung und Ausschneiden eines Objektes (schraube.png)
Bonusaufgabe: Kunst nachbauen
Schreiben Sie ein Python-Programm, das das Bild Spectrum Colors arranged by Chance von Ellsworth Kelly nachahmt.
26.3 Quellen und Lesetipps
Die Bilder sind einem Histogramm-Tutorial der Online-Community Cambridge in Colour entnommen.
26.4 Lösungen
Aufgabe: Ziffern-Histogramm berechnen
Die folgende Funktion berechnet ein Histogramm der übergebenen Liste von Ziffern.
def digit_histogram(digits):
counts = [0,0,0,0,0,0,0,0,0,0]
for digit in digits:
counts[digit] = counts[digit] + 1
return counts
Aufgabe: Grauwerte berechnen
Die Funktion luminosity berechnet einen gewichteten Mittelwert der drei Farbkanäle
und rundet das Ergebnis anschließend zu einer ganzen Zahl.
def luminosity(color):
r = color[0]
g = color[1]
b = color[2]
return round(0.3*r + 0.59*g + 0.11*b)
Wir können sie in der Prozedur desaturate anstelle von average verwenden.
Aufgabe: Histogramm zeichnen
Die Funktion render_histogram erzeugt ein Bild der Größe 256 mal 256 Pixel. Sie berechnet einen Skalierungsfaktor in Abhängigkeit der größten im Histogram vorkommenden Anzahl, damit diese genau am oberen Bildrand dargestellt wird. In einer Schleife wird dann für jeden Grauwert mit einer weiteren Schleife eine vertikale Linie gezeichnet, die die im Histogram gespeicherte Anzahl anzeigt.
def render_histogram(histogram):
width = 256
height = 256
image = Image.new("RGB", (width, height), (255,255,255))
scaling = max(histogram) / height
for x in range(0,width):
for z in range(1,round(histogram[x] / scaling)):
y = max(0,height-z)
image.putpixel((x,y), (0,0,0))
return image
Aufgabe: Kontrastveränderung programmieren
Die Funktion contrast_adjustment berechnet eine Abbildung von Grauwerten in Grauwerte mit Hilfe einer Geradengleichung für die geforderte Gerade. Jeder neue Grauwert wird nach seiner Berechnung auf den zulässigen Wertebereich von 0 bis 255 beschränkt und dann in die zurückgegebene Abbildung eingetragen.
def contrast_adjustment(factor):
gray_map = [0] * 256
for gray in range(0,256):
new_gray = round(factor * gray + 128 * (1-factor))
new_gray = max(0, new_gray)
new_gray = min(new_gray, 255)
gray_map[gray] = new_gray
return gray_map
Die Prozedur save_with_changed_contrast liest ein Bild aus einer gegebenen Datei ein, berechnet dann mit contrast_adjustment eine Abbildung zwischen Grauwerten aus dem gegbeenen Faktor, wendet diese auf das eingelesene Bild an und speichert das Ergebnis unter einem neuen Namen.
def save_with_changed_contrast(base_name, factor):
image = Image.open(base_name + ".jpg")
gray_map = contrast_adjustment(factor)
change_pixels(image, gray_map)
image.save(base_name + "_cont" + str(factor) + ".jpg")
Bonusaufgabe: Kunst nachbauen
Hier ist ein Programm, das 1000 Farben zufällig auf einem schwarzen Bild aus 1600 Blöcken verteilt.
from PIL import Image
from random import randint
black = (0,0,0)
img_size = 400
block_size = 10
colored_blocks = Image.new("RGB", (img_size,img_size), black)
block_count = img_size / block_size
spectrum_colors = [None] * 1000
for r in range(0,10):
for g in range(0,10):
for b in range(0,10):
spectrum_colors[100*r+10*g+b] = (25*r,25*g,25*b)
def fill_square(img,from_x,from_y,size,color):
for x in range(from_x,from_x+size):
for y in range(from_y,from_y+size):
img.putpixel((x,y), color)
for i in range(0,len(spectrum_colors)):
color = spectrum_colors[i]
rx = block_size * randint(0, block_count-1)
ry = block_size * randint(0, block_count-1)
fill_square(colored_blocks,rx,ry,block_size,color)
colored_blocks.save("colored_blocks.png")
27. Backtracking
27.1 Suchbäume
Haufig kann man bei Suchproblemen Teillösungen betrachten und schrittweise zu einer Problemlösung erweitern. Unterschiedliche Teillösungen bieten oft unterschiedliche Möglichkeiten, sie zu erweitern, so dass der sogenannte Suchraum aller (Teil-)Lösungen als Baumstruktur aufgefasst werden kann. Die Blätter dieses Baumes sind Teillösungen, die nicht mehr erweitert werden können. Diese können erfolgreiche Problemlösungen darstellen oder Fehlschläge. Die inneren Knoten des Baumes entsprechen Teillösungen und deren Nachfolgeknoten entsprechen ihren Erweiterungen.
Beim Lösen eines Sudoku-Puzzles zum Beispiel, entsprechen vollständig ausgefüllte Puzzles den Blättern im Suchbaum und konfliktfrei ausgefüllte Puzzles den Lösungen. Die inneren Knoten sind teilweise ausgefüllte Puzzles, die dadurch erweitert werden können, dass ein bisher freies Feld mit einer Ziffer belegt wird.
Die Verzweigungen im Suchbaum entstehen durch Alternativen bei der Erweiterung von Teillösungen und Backtracking ist eine Technik, diese Alternativen systematisch auszuprobieren. Dazu merkt man sich bei der Auswahl einer Alternative, welche weiteren Alternativen es gibt. Bei einem Fehlschlag nimmt man dann die zuletzt vorgenommene Auswahl zurück und probiert stattdessen die nächste Alternative. Diese Rückkehr zur zuletzt betrachteten Alternative gibt der Programmiertechnik Backtracking ihren Namen.
Ein Algorithmus, der mit Hilfe von Backtracking nach der ersten Lösung eines Problems sucht, kann durch Kombination einer Schleife mit Rekursion formuliert werden. Er gibt zurück, ob eine Teillösung lösbar ist und muss mit einer initialen Teillösung aufgerufen werden.
Teillösung lösbar?
Falls Teillösung vollständig ist,
gib zurück, ob Teillösung gültig ist.
Durchlaufe jede Erweiterung der Teillösung.
Falls Erweiterung lösbar,
gib wahr zurück.
Gib falsch zurück.
Die Schleife, die die Erweiterungen einer Teillösung durchläuft, enthält in ihrem Rumpf einen rekursiven Aufruf des Algorithmus, um zu testen, ob die Erweiterungen lösbar sind. Falls keine der Erweiterungen lösbar ist, ist die Teillösung auch nicht lösbar, in diesem Fall wird also falsch zurück gegeben. Dieser Algorithmus basiert auf Unter-Algorithmen
- zum Testen, ob eine (Teil-)lösung vollständig ist,
- zum Testen, ob eine (Teil-)lösung gültig ist und
- zur Berechnung aller Erweiterungen einer Teillösung.
Unterschiedliche Backtracking-Algorithmen unterscheiden sich im Wesentlichen in diesen drei Aspekten, während das Grundgerüst gleich bleibt.
27.2 Damenproblem
Das Damenproblem ist ein einfach zu beschreibendes Problem, das sich elegant durch Backtracking lösen lässt und dabei erlaubt, die beschriebenen Aspekte eines Suchproblems zu verdeutlichen. Es besteht darin, acht Damen so auf einem Schachbrett zu platzieren, dass sie sich weder horizontal noch vertikal noch diagonal schlagen können. Im Folgenden ist eine gültige Platzierung von vier Damen auf einem entsprechend verkleinerten Schachbrett dargestellt.

Um die Platzierung von Damen auf einem Schachbrett in Python
darzustellen, können wir ausnutzen, dass diese, damit sie sich nicht
horizontal schlagen können, in unterschiedlichen Zeilen (Reihen) platziert
werden müssen. Wir stellen sie deshalb als Array aus Zahlen dar und
speichern dabei im ersten Eintrag des Arrays, in welcher Spalte (Linie) die
erste Dame steht, im zweiten Eintrag die Spalte der zweiten Dame und
so weiter.
Wir durchlaufen dabei die Zeilen von oben nach unten
und zählen die Spalten von Null beginnend.
Zum Beispiel entspricht das Array [2,0,3,1] der oben gezeigten
Platzierung von vier Damen auf einem 4x4 Schachbrett.
Die Prozedur print_queens gibt eine so dargestellte Platzierung von
Damen im Terminal aus.
def print_queens(queens):
for i in range(0, len(queens)):
print(" " * queens[i] + "Q")
Die Ausgabe von print_queens([2,0,3,1]) ähnelt der obigen grafischen
Darstellung.
Q
Q
Q
Q
Um das Damenproblem mit Hilfe von Backtracking zu lösen,
implementieren wir eine Funktion is_complete, die testet, ob eine so
dargestellte Platzierung vollständig ist. Da wir acht Damen auf einem
richtigen Schachbrett platzieren wollen, testen wir dazu, ob das
Array, die Größe acht hat. Unser Algorithmus soll also dem Array
schrittweise Einträge hinzufügen, bis dieses acht Einträge enthält.
BOARD_SIZE = 8
def is_complete(queens):
return len(queens) == BOARD_SIZE
Wir verwenden eine Konstante1 BOARD_SIZE für die Anzahl der Damen,
die auf dem Schachbrett platziert werden sollen. Diese definieren wir global (also außerhalb der Definition von is_complete), um sie auch in anderen Definitionen verwenden zu können.
Um zu testen, ob eine Platzierung gültig ist, müssen wir testen, ob alle Damen vor Angriffen anderer sicher sind. Da wir durch die Darstellung bereits sicher gestellt haben, dass Damen sich nicht horizontal schlagen können, brauchen wir dazu nur noch zu testen, ob sie sich vertikal oder diagonal bedrohen. Dazu durchlaufen wir jede Dame mit Hilfe einer Zählschleife und testen dann in einer weiteren Zählschleife, ob sie vor später platzierten Damen sicher ist.
def is_safe(queens):
# search all pairs of different queens
for i in range(0, len(queens)):
for j in range(i + 1, len(queens)):
# queens in same column
if queens[i] == queens[j]:
return False
# row distance equals column distance: queens on same diagonal
if j - i == abs(queens[j] - queens[i]):
return False
# found no attack
return True
Ob sich Damen vertikal bedrohen, erkennen wir daran, ob sich die Spalten zweier verschiedener Damen gleichen. Um zu testen, ob sich Damen diagonal bedrohen, vergleichen wir deren Spaltenabstand mit dem Zeilenabstand. Sind diese gleich, stehen die Damen auf der selben Diagonale und können sich schlagen. Zur Berechnung des Spaltenabstandes verwenden wir den Absolutbetrag. Da wir für jede in der äußeren Schleife durchlaufene Dame nur später platzierte Damen betrachten, ist dies für den Zeilenabstand nicht nötig.
Schließlich implementieren wir noch eine Funktion place_next, die
eine Platzierung um eine weitere Dame erweitert. Diese fügt dem Array
einen Eintrag zwischen null und sieben hinzu und gibt ein Array aller
so erzeugten Arrays zurück.
def place_next(queens):
extensions = [None] * BOARD_SIZE
for q in range(0, BOARD_SIZE):
extensions[q] = queens + [q]
return extensions
Wir können nun den zuvor umgangssprachlich formulierten Algorithmus als
Funktion is_solvable implementieren. Statt im Schleifenrumpf eine
return-Anweisung zu verwenden, speichern wir in einer Variablen
solvable, ob eine Lösung gefunden wurde. Diese können wir dann in
der Bedingung einer bedingten Schleife abfragen, um die Betrachtung
überflüssiger Alternativen zu vermeiden.
def is_solvable(queens):
if is_complete(queens):
return is_safe(queens)
exts = place_next(queens)
for index in range(0, len(exts)):
if is_solvable(exts[index]):
return True
return False
Falls die übergebene Teillösung vollständig ist, wird zurückgegeben,
ob diese gültig ist. Falls nicht, werden alle Erweiterungen der
übergebenen Teillösung berechnet und in der Variablen qs
gespeichert. Die anschließende Schleife durchläuft die Erweiterungen,
bis mit Hilfe eines rekursiven Aufrufs eine lösbare Erweiterung
gefunden wurde.
Mit den gezeigten Definitionen läuft der Aufruf is_solvable([]) für
einige Sekunden und liefert schließlich das Ergebnis True zurück,
zeigt also an, dass das Damenproblem für acht Damen lösbar ist. Dabei
werden alle Platzierungen von acht Damen auf einem Schachbrett
nacheinandner daraufhin getestet, ob sich Damen bedrohen, bis die
erste sichere Platzierung gefunden wurde. Da (bis zur ersten Lösung)
der komplette Suchraum aller Platzierungen von acht Damen auf einem
Schachbrett durchsucht wird, spricht man von einem sogenannten brute
force Algorithmus. Der Suchraum wird mit voller Kraft vorraus aber
auch blind durchsucht und erst vollständige Platzierungen werden auf
Gültigkeit überprüft.
Da wir bereits unvollständige Teillösungen auf Gültigkeit überprüfen können, können wir die Laufzeit des Algorithmus deutlich verbessern. Wenn sich zum Beispiel schon die beiden zuerst platzierten Damen bedrohen, brauchen die restlichen sechs gar nicht mehr platziert zu werden. Dadurch werden große Teile des Suchbaums gar nicht erst durchlaufen.
Wir implementieren diese Idee,
indem wir die Abbarbeitung des Rumpfes von is_solvable vorzeitig beenden,
wenn die übergebene Teillösung nicht gültig ist.
Dazu können wir die folgende optionale Anweisung
am Anfang des Funktionsrumpfes notieren.
if not is_safe(queens):
return False
Nach dieser Änderung liefert der Aufruf is_solvable([]) das Ergebnis
True ohne merkliche Verzögerung. Falls wie hier bereits
Teillösungen auf ihre Gültigkeit überprüft werden können, kann auf
diese Weise die Laufzeit des Backtracking-Verfahrens oft erheblich
verbessert werden.
Dass das Damenproblem lösbar ist, haben wir möglicherweise bereits
vorher vermutet. Um die gefundene Platzierung auszugeben, fügen wir
in der bedingten Anweisung zu Beginn der Definition von is_solvable einen
Aufruf von print_queens hinzu.
if is_complete(queens):
print_queens(queens)
return True
Da is_solvable ungültige Teillösungen vorher verwirft,
ist der Test is_safe(queens) für vollständige Teillösungen nun
überflüssig und wir ersetzen ihn durch True. Der Aufruf
is_solvable([]) gibt nun die folgende Darstellung einer sicheren Platzierung
von acht Damen auf einem Schachbrett aus.
Q
Q
Q
Q
Q
Q
Q
Q
-
Python bietet keine Möglichkeit, Zuweisungen an Variablen zu verhindern. Per Konvention wird aber Variablen, die nur aus Großbuchstaben und Unterstrichen bestehen, nach der Initialisierung kein neuer Wert zugewiesen. ↩︎
27.3 Aufgaben und Lösungen
27.3.1 Aufgaben
Aufgabe: Ablauf veranschaulichen
Stelle das rekursive Ablaufschema der Funktion is_solvable für BOARD_SIZE = 4 verkürzt dar, wie im Kapitel Rekursion beschrieben. Die verkürzte Darstellung sollte nur den Ablauf bis zur ersten Abbruchsituation und den Pfad bis zur Ausgabe der Lösung enthalten.
Aufgabe: Lösungen zählen
Wandeln Sie das Programm zur Lösung des Damenproblems so ab,
dass es nicht nach der ersten Lösung abbricht,
sondern die Anzahl aller Lösungen als Ergebnis zurückliefert.
Implementieren Sie dazu analog zu is_solvable
eine leicht abgewandelte Funktion solution_count,
die diese Anzahl zurück liefert.
Wie viele Lösungen hat das Damenproblem für acht Damen?
Bis zu wievielen Damen können Sie die Anzahl aller Lösungen des Damenproblems in annehmbarer Zeit berechnen?
Aufgabe: Sudoku lösen
Schreiben Sie ein Python-Programm, das Backtracking verwendet, um nach einer Lösung für ein Sudoku-Puzzle zu suchen. Testen Sie es zum Beispiel mit der folgenden Vorbelegung, bei der freie Felder als 0 dargestellt sind:
PUZZLE = [
[0, 0, 0, 0, 7, 3, 0, 1, 2],
[0, 1, 0, 2, 0, 6, 4, 0, 0],
[0, 0, 2, 0, 0, 0, 5, 0, 8],
[0, 0, 3, 0, 0, 4, 0, 0, 0],
[4, 9, 8, 0, 0, 1, 0, 0, 0],
[0, 0, 6, 0, 0, 5, 0, 0, 0],
[0, 0, 4, 0, 0, 0, 6, 0, 1],
[0, 6, 0, 3, 0, 7, 2, 0, 0],
[0, 0, 0, 0, 6, 8, 0, 4, 5],
]
Zur Implementierung der Gültigkeitsbedingung ist die vordefinierte Funktion set hilfreich, die (nicht mutierend) Duplikate aus einem Array entfernt. Zum Beispiel ist len(entries) == len(set(entries)) genau dann True, wenn alle Elemente von entries verschieden sind.
27.3.2 Lösungen
Aufgabe: Lösungen zählen
Die Funktion solution_count gibt statt eines Wahrheitswertes die Anzahl der gültigen Lösungen zurück. Diese Anzahl erhalten wir, indem wir in der Schleife, die die Erweiterungen durchläuft, die Teilergebnisse der einzelnen Erweiterungen aufaddieren. Anders als das Programm aus der Vorlesung bricht die Schleife nicht bei der ersten gefundenen Lösung ab sondern durchläuft alle.
def solution_count(queens):
if not is_safe(queens):
return 0
if is_complete(queens):
return 1
exts = place_next(queens)
count = 0
for index in range(0, len(exts)):
count = count + solution_count(exts[index])
return count
Für größere Zahlen lohnt es sich, den in is_safe implementierten Test zu optimieren. Da wir Damen schrittweise hinzufügen, genügt es, nur für die zuletzt hinzugefügte Dame zu testen, ob sie eine der anderen bedroht:
# assumes that only the last queen may be unsafe
def is_safe(queens):
j = len(queens) - 1
# search all previous queens
for i in range(0, len(queens) - 1):
# queens in same column
if queens[i] == queens[j]:
return False
# row distance equals column distance: queens on same diagonal
if j - i == abs(queens[j] - queens[i]):
return False
# found no attack
return True
Eine weitere Interessante Optimierung ergibt sich aus der Reihenfolge, in der Erweiterungen gebildet werden. In der Praxis zeigt sich nämlich, dass die erste Lösung deutlich schneller gefunden wird, wenn die Erweiterungen in zufälliger Reihenfolge durchlaufen werden:
def place_next(queens):
extensions = [None] * BOARD_SIZE
for q in range(0, BOARD_SIZE):
extensions[q] = queens + [q]
shuffle(extensions)
return extensions
Die Prozedur shuffle vertauscht die Elemente eines Arrays in zufälliger Reihenfolge und kann mit der Anweisung from random import shuffle importiert werden.
Mit den gezeigten Änderung können wir eine Lösung für sehr große Schachbretter in akzeptabler Zeit berechnen.
Zum Beispiel wird eine Lösung für 100 Damen oft nach wenigen Sekunden angezeigt.
Die Suche nach allen Lösungen wird durch die Randomisierung nicht beschleunigt,
profitiert aber ebenfalls vom vereinfachten Gültigkeitstest is_safe.
Aufgabe: Sudoku lösen
Wir definieren zunächst eine Prozudur zur Ausgabe eines Sudoku-Puzzles.
def print_puzzle(puzzle):
for i in range(0, len(puzzle)):
line = ""
for j in range(0, len(puzzle[i])):
if puzzle[i][j] == 0:
line = line + " ."
else:
line = line + " " + str(puzzle[i][j])
print(line)
Um zu testen, ob ein Puzzle vollständig ausgefüllt wurde, suchen wir nach Nullen.
def is_complete(puzzle):
for i in range(0, len(puzzle)):
for j in range(0, len(puzzle[i])):
if puzzle[i][j] == 0:
return False
return True
Der Test der Gültigkeitsbedingung wendet eine Hilfsfunktion all_valid auf alle Zeilen, alle Spalten und alle Quadrate an.
def is_valid(puzzle):
if not all_valid(puzzle):
return False
if not all_valid(columns(puzzle)):
return False
if not all_valid(squares(puzzle)):
return False
return True
Die Hilfsfunktion all_valid erwartet ein geschachteltes Array von Zahlen und prüft, ob die enthaltenen Arrays Duplikate enthalten.
def all_valid(areas):
for i in range(0, len(areas)):
entries = non_zero_entries(areas[i])
# check for duplicates using the set function
if len(entries) != len(set(entries)):
return False
return True
Die hier verwendete Funktion non_zero_entries erwartet ein Array von Zahlen als Argument und liefert ein neues Array derjenigen Zahlen zurück, die ungleich Null sind.
def non_zero_entries(area):
result = []
for i in range(0, len(area)):
if area[i] != 0:
result.append(area[i])
return result
Spalten berechnen wir mit einer geschachtelten Zählschleife.
def columns(puzzle):
result = []
for j in range(0, len(puzzle[0])):
column = []
for i in range(0, len(puzzle)):
column.append(puzzle[i][j])
result.append(column)
return result
Die Berechnung der Quadrate ist etwas komplizierter, aber ebenfalls mit einer geschachtelten Zählschleife möglich.
def squares(puzzle):
result = []
row = 0
for i in range(0, 3):
col = 0
for j in range(0, 3):
result.append(
puzzle[row][col : col + 3]
+ puzzle[row + 1][col : col + 3]
+ puzzle[row + 2][col : col + 3]
)
col = col + 3
row = row + 3
return result
Um Erweiterungen einer Teillösung zu berechnen, suchen wir zunächst nach der Position eines freien Feldes und tragen dann neue Zahlen in Kopien der ursprünglichen Lösung ein. Wir erzeugen die Erweiterungen in zufälliger Reihenfolge.
def extensions(puzzle):
pos = zero_position(puzzle)
row = pos[0]
col = pos[1]
result = []
for number in range(1, 10):
extension = copy(puzzle)
extension[row][col] = number
result.append(extension)
shuffle(result)
return result
Die Position eines freien Feldes suchen wir wieder mit einer geschachtelten Zählschleife.
def zero_position(puzzle):
for i in range(0, len(puzzle)):
for j in range(0, len(puzzle[i])):
if puzzle[i][j] == 0:
return [i, j]
return None
Die folgende Funktion kopiert ein geschachteltes Array von Zahlen.
def copy(puzzle):
result = []
for i in range(0, len(puzzle)):
result.append(puzzle[i] + [])
return result
Schließlich implementieren wir den Backtracking-Algorithmus unter Verwendung der definierten Hilfsfunktionen.
def is_solvable(puzzle):
if not is_valid(puzzle):
return False
if is_complete(puzzle):
print_puzzle(puzzle)
return True
exts = extensions(puzzle)
for index in range(0, len(exts)):
if is_solvable(exts[index]):
return True
return False
Der Aufruf is_solvable(PUZZLE) liefert True zurück und erzeugt vorher die folgende Ausgabe.
6 4 5 8 7 3 9 1 2
8 1 9 2 5 6 4 3 7
7 3 2 4 1 9 5 6 8
2 5 3 7 8 4 1 9 6
4 9 8 6 2 1 7 5 3
1 7 6 9 3 5 8 2 4
3 8 4 5 9 2 6 7 1
5 6 1 3 4 7 2 8 9
9 2 7 1 6 8 3 4 5
28. Künstliche Intelligenz für Spiele
28.1 Zwei-Personen-Spiele und automatisches Spiel
Im folgenden betrachten wir Spiele, in denen zwei Spieler abwechselnd ziehen, (anders als bei vielen Kartenspielen) keine Information geheim bleibt und (anders als bei Würfelspielen) der Zufall keine Rolle spielt. Beispiele für solche Spiele sind Schach, Dame, Reversi, Tic Tac Toe oder Vier Gewinnt.
Wir werden Klassen definieren, die es erlauben Zwei-Personen-Spiele darzustellen und Klassen, die es erlauben, automatische Spieler für solche Spiele zu definieren. Da die Algorithmen unabhängig von den konkreten Spielen definiert werden können, trennen wir die Definition von Spielern von der Definition von Spielen.
Spieler für Zwei-Personen-Spiele sind Objekte der Klasse Player.
class Player:
def __init__(self, name):
self.name = name
def set_game(self, game):
self.game = game
def __str__(self):
return self.name
Zur Darstellung auf dem Bildschirm geben wir Spielern einen Namen, der im Konstruktor übergeben wird. Unterklassen der Klasse Player sollen eine Methode select_move implementieren, die einen ausgewählten Zug im Spiel zurückliefert, dass im Attribut game gespeichert ist. Unterklassen der Klasse Game sollen dazu eine Methode valid_moves definieren, die ein Array gültiger Züge liefert, aus dem Spieler wählen können.
Zwei-Personen-Spiele sind Objekte der Klasse Game:
class Game:
def __init__(self, player1, player2):
player1.set_game(self)
player2.set_game(self)
self.current_player = player1
self.waiting_player = player2
# weitere Definitionen folgen
Objekten der Klasse Game werden im Konstruktor zwei Spieler übergeben. Der zuerst übergebene Spieler beginnt das Spiel, und nach seinem Zug wechselt das Zugrecht. Dazu vertauscht die Methode next_turn die Rollen beider Spieler.
def next_turn(self):
player = self.current_player
self.current_player = self.waiting_player
self.waiting_player = player
Die Methode play wird aufgerufen um ein Spiel zu starten und seine Durchführung auf dem Bildschirm auszugeben.
def play(self):
while not self.has_ended():
print(self)
move = self.current_player.select_move()
self.make_move(move)
self.next_turn()
print(self)
In jedem Schritt wird ein von dem Spieler, der an der Reihe ist, ausgewählter Zug ausgeführt, bis das Spiel beendet ist. Dazu müssen die Methoden has_ended und make_move von Unterklassen der Klasse Game implementiert werden.
Vor und nach jedem Zug wird das Spiel auf dem Bildschirm ausgegeben. Die folgende Methode gibt eine Zeichenkette zurück, die den Zustand des Spiels beschreibt.
def __str__(self):
if self.has_ended():
w = self.winner()
if w == None:
return "draw"
return str(w) + " won"
return str(self.current_player) + "'s turn"
Ist das Spiel beendet, so wird mit Hilfe der Methode winner ermittelt, wer gewonnen hat, und das Ergebnis zurück geliefert. Auch diese Methode muss also in Unterklassen implementiert werden. Läuft das Spiel noch, liefert __str__ zurück, wer an der Reihe ist.
Die gezeigten Definitionen der Klassen Player und Game speichern wir in two_player_games.py, um sie zur Definition konkreter Spiele und Spieler in anderen Dateien verwenden zu können.
Als Beispiel für ein einfaches Zwei-Personen-Spiel implementieren eine einfache Version des Nim-Spiel’s als Unterklasse von Game.
class SimpleNim(Game):
def __init__(self, player1, player2, count):
super().__init__(player1, player2)
self.count = count
# weitere Definitionen folgen
Das Nim-Spiel wird mit einem Haufen Streichhölzern gespielt, dessen Größe im Konstruktor übergeben wird. Die Methode __str__ gibt die Anzahl der Streichhölzer neben dem Spielzustand zurück, den die überschriebene Methode der Oberklasse liefert.
def __str__(self):
return str(self.count) + "\tmatches, " + super().__str__()
Die Spieler nehmen abwechselnd Streichhölzer vom Haufen, bis keine mehr da sind.
def has_ended(self):
return self.count == 0
Die Methode make_move entfernt so viele Streichhölzer vom Haufen, wie im übergebenen Zug angegeben sind.
def make_move(self, number):
self.count = self.count - number
Wer das letzte Streichholz nimmt, verliert das Spiel. Es gewinnt also der Spieler, der bei Spielende an der Reihe ist.
def winner(self):
return self.current_player
Ein gültiger Zug entfernt ein bis drei Streichhölzer vom Haufen, sofern noch so viele dort liegen. Die Höchstzahl zu entfernender Streichhölzer wird mit der Methode min der Klasse Array berechnet.
def valid_moves(self):
moves = []
for number in range(1, 1 + min(3, self.count)):
moves.append(number)
return moves
Um unsere Implementierung zu testen, definieren wir noch eine Klasse für Spieler, die in jedem Zug einen zufälligen der gültigen Züge auswählen.
from random import shuffle
class RandomPlayer(Player):
def select_move(self):
moves = self.game.valid_moves()
shuffle(moves)
return moves[0]
Wir können nun ein Spiel zwischen Zufallsspielern starten und den Verlauf beobachten.
>>> alice = RandomPlayer("Alice")
>>> bob = RandomPlayer("Bob")
>>> SimpleNim(alice,bob,21).play()
21 matches, Alice's turn
19 matches, Bob's turn
18 matches, Alice's turn
16 matches, Bob's turn
15 matches, Alice's turn
12 matches, Bob's turn
10 matches, Alice's turn
9 matches, Bob's turn
8 matches, Alice's turn
6 matches, Bob's turn
5 matches, Alice's turn
3 matches, Bob's turn
2 matches, Alice's turn
1 matches, Bob's turn
0 matches, Alice won
28.1.1 Aufgaben
Aufgabe: Interaktiven Spieler implementieren
Erweitern Sie die Klassendefinitionen um eine Unterklasse Human der Klasse Player, die es erlaubt, den auszuwählenden Zug im Terminal einzugeben. Lesen Sie vom Benutzer eine Zahl zwischen eins und der Anzahl gültiger Züge ein und verwenden Sie diese (damit der definierte Spieler für beliebige Spiele verwendet werden kann) als Position im Array gültiger Züge: Bei Eingabe einer 1 soll also der erste gültige Zug zurückgegeben werden, bei einer 2 der zweite und so weiter. Fragen Sie dabei so lange Eingaben ab, bis eine gültige Position eingegeben wurde.
Gehen Sie davon aus, dass durch die Anzeige des Spieles (mit Hilfe von dessen __str__-Methode) klar wird, welche Zahl welchem Zug entspricht. Sie brauchen die gültigen Züge also nicht gesondert auf dem Bildschirm auszugeben.
Nach der Definition Ihrer Klasse, sollten Sie wie folgt gegen einen Zufallsspieler im Nim-Spiel antreten können.
>>> alice = Human("Alice")
>>> bob = RandomPlayer("Bob")
>>> SimpleNim(alice,bob,21).play()
21 matches, Alice's turn
Your choice: 2
19 matches, Bob's turn
17 matches, Alice's turn
Your choice: 1
16 matches, Bob's turn
15 matches, Alice's turn
Your choice: 2
13 matches, Bob's turn
11 matches, Alice's turn
Your choice: 1
10 matches, Bob's turn
9 matches, Alice's turn
Your choice: 2
7 matches, Bob's turn
4 matches, Alice's turn
Your choice: 1
3 matches, Bob's turn
2 matches, Alice's turn
Your choice: 1
1 matches, Bob's turn
0 matches, Alice won
Aufgabe: Verallgemeinertes Nim-Spiel implementieren
In der verallgemeinerten Variante des Nim-Spiels wird mit mehreren Haufen von Streichhölzern gespielt. Ein Zug besteht darin, beliebig viele Streichhölzer (mindestens einen, höchstens alle) aus einem der Haufen heraus zu nehmen. Verloren hat, wer das letzte Streichholz nehmen muss.
Implementieren Sie dieses Spiel in einer Unterklasse Nim der Klasse Game. Überschreiben Sie dazu die Methoden __init__, __str__, has_ended, make_move, winner und valid_moves mit geeigneten Implementierungen. Die Ausgabe der Streichholzhaufen kann so aussehen wie im folgenden Beispiel gezeigt.
Hinweis: Die Methode join auf Zeichenketten ist hilfreich mehrere Zeichenketten aneinander zu hängen.
Zum Beispiel liefert "+".join(["a","b","c"]) den Wert "a+b+c" zurück.
>>> alice = Human("Alice")
>>> bob = RandomPlayer("Bob")
>>> Nim(alice,bob,[1,3,5]).play()
Alice's turn
1
2 3 4
5 6 7 8 9
Your choice: 7
Bob's turn
1
2 3 4
5 6
Alice's turn
1
2 3
4 5
Your choice: 1
Bob's turn
1 2
3 4
Alice's turn
1
2 3
Your choice: 3
Bob's turn
1
Alice won
Jeder Haufen wird in einer Zeile ausgegeben. Jede Zeile enthält so viele Zahlen, wie Streichölzer im entsprechenden Haufen liegen. Die Zahlen sind fortlaufend nummeriert. Bei Auswahl eines Zuges werden aus dem entsprechenden Haufen alle Streichhölzer bis zur eingegebenen Zahl entfernt.
Bonusaufgabe: Tic-Tac-Toe implementieren
Implementieren Sie das Spiel Tic Tac Toe als Unterklasse der Klasse Game. Ein Spiel zwischen Mensch und Zufallsspieler kann zum Beispiel so ausshehen:
irb> xavier = Human("Xavier")
irb> olga = RandomPlayer("Olga")
irb> TicTacToe(xavier,olga).play()
Xavier's turn
1 2 3
4 5 6
7 8 9
Your choice: 1
Olga's turn
X 1 2
3 4 5
6 7 8
Xavier's turn
X O 1
2 3 4
5 6 7
Your choice: 3
Olga's turn
X O 1
2 X 3
4 5 6
Xavier's turn
X O 1
2 X 3
4 O 5
Your choice: 5
Xavier wins
X O 1
2 X 3
4 O X
Belegte Felder werden hier mit dem Anfangsbuchstaben des entsprechenden Spielers gekennzeichnet; freie Felder mit einer Zahl, die als Zug eingegeben werden kann.
Hinweis: Der Python-Operator in ist hilfreich, um zu testen, ob ein Element in einem Array enthalten ist.
Zum Beispiel hat der Ausdruck "a" in ["a","b","c"] den Wert True.
28.2 Bewertung von Spielzügen
Um gute Spieler zu programmieren, müssen wir statt zufälligen sinnvolle Züge aus den gültigen auswählen. Diese Auswahl ist der Kern der in diesem Kapitel vorgestellten Algorithmen, die wir im folgenden schrittweise entwickeln.
Vollständige Suche im Spielbaum
In einfachen Spielen können wir alle Zugmöglichkeiten systematisch überprüfen, indem wir (ähnlich wie beim Backtracking) alle Folgezüge durchsuchen, bis das Spiel beendet ist. Dadurch entsteht eine Baumstruktur, an deren Blättern beendete Spiele stehen. Jeder innere Knoten verzweigt entsprechend der in diesem Zustand gültigen Züge.
Statt bei jeder Verzweigung Kopien der Spielzustände anzulegen, wollen wir das Spiel-Objekt mutieren. Dazu müssen Spiele neben der Methode make_move eine Methode undo_move definieren, die einen übergebenen Zug rückgängig macht. Dann können Züge probeweise mit make_move ausgeführt und vor dem Ausprobieren weiterer Züge mit undo_move wieder rückgängig gemacht werden.
Für das (vereinfachte) Nim-Spiel definieren wir die Methode undo_move wie folgt.
def undo_move(self, number):
self.count = self.count + number
Die im übergebenen Zug herunter genommen Streichhölzer werden hier also wieder auf den Haufen drauf gelegt.
Verglichen mit Backtracking kommt bei Spielbäumen erschwerend hinzu, dass zwei Spieler mit unterschiedlichen Zielen gegeneinander antreten. Was für den einen Spieler ein günstiger Zug ist, ist für den anderen Spieler ein ungünstiger. Beide Spieler versuchen, Züge so auszuwählen, dass sie ein möglichst gutes Ergebnis erzwingen können. Ist kein Sieg erzwingbar, kann möglicherweise zumindest ein Unentschieden gesichert werden, um eine Niederlage zu vermeiden.
Für Spiele im Endzustand können wir diese drei Ergebnisse als Zahl (1 für einen Sieg, 0,5 für ein Unentschieden und 0 für eine Niederlage) ausdrücken.
Wir verwenden Zahlen zwischen Null und Eins,
um bei Bewertungen einfach die Perspektive wechseln zu können.
Ist e die Bewertung einer Spielsituation aus Sicht des einen Spielers,
dann ergibt sich eine Bewertung aus Sicht des anderen Spielers als 1-e.
Kann der Gegner einen Sieg erzwingen, ist uns eine Niederlage sicher (und umgekehrt).
Alternativ könnten wir beliebige Zahlen erlauben und diese beim Perspektivwechsel negieren.
Unsere Wahl erlaubt die Interpretation der Bewertung als Gewinnwarscheinlichkeit.
Zur Berechnung dieser Bewertung (aus Sicht des Spielers, der an der Reihe ist) fügen wir der Klasse Game die folgende Methode hinzu.
def eval_on_end(self):
if self.winner() == None: # draw
return 0.5
if self.current_player is self.winner():
return 1.0
return 0.0
Wir definieren nun eine Klasse SearchingPlayer für Spieler, die den Spielbaum systematisch bis zum Ende durchsuchen. Die vier ersten Methoden können später von Unterklassen überschrieben werden, um die Suche zu beeinflussen.
class SearchingPlayer(Player):
def make_move(self, move, count):
self.game.make_move(move)
self.game.next_turn()
def undo_move(self, move, count):
self.game.undo_move(move)
self.game.next_turn()
def should_stop(self):
return self.game.has_ended()
def eval_on_stop(self):
return self.game.eval_on_end()
# weitere Definitionen folgen
In der Klasse SearchingPlayer sind die gezeigten Methoden durch bereits besprochene Methoden auf Spielen implementiert. Die teilweise abweichenden Namen und Parameter klären wir später.
Zur Definition der Methode select_move definieren wir zunächst gegenseitig rekursive Hilfsmethoden zur Bewertung von Spielzügen und Spielzuständen.
Die Methode eval_move berechnet die Bewertung eines Zuges anhand der aus diesem Zug resultierenden Spielsituation.
def eval_move(self, moves, index):
self.make_move(moves[index], len(moves))
eval = 1 - self.eval_by_search()
self.undo_move(moves[index], len(moves))
return eval
Hier werden die oben definierten Methoden make_move und undo_move aufgerufen,
denen neben dem Spielzug auch die Anzahl aller verfügbaren Spielzüge übergeben wird,
die wir uns später zunutze machen.
Die Bewertung der Spielsituation nach Ausführung des Zuges erfolgt mit der Methode eval_by_search,
die wie folgt definiert ist.
Da ihr Ergebnis aus Sicht des anderen Spielers zu interpretieren ist,
berechnen wir eine Bewertung aus der Sicht des ursprünglich ziehenden Spielers
mit Hilfe der oben erwähnten Subtraktion von Eins.
def eval_by_search(self):
if self.should_stop():
return self.eval_on_stop()
moves = self.game.valid_moves()
best_eval = -1
for index in range(0, len(moves)):
eval = self.eval_move(moves, index)
if eval > best_eval:
best_eval = eval
return best_eval
Diese Methode berechnet eine Bewertung mit eval_on_stop,
wenn die Suche beendet werden soll und liefert ansonsten die
(rekursiv mit eval_move berechnete)
bestmögliche Bewertung zurück, die durch gültige Züge erreichbar ist.
Die Definition der Methode select_move ähnelt der von eval_search,
liefert aber einen Spielzug zurück und keine Bewertung.
Außerdem wird die rekursive Suche nur gestartet,
wenn es überhaupt mehrere Züge zur Auswahl gibt.
def select_move(self):
moves = self.game.valid_moves()
if len(moves) == 1:
return moves[0]
best_eval = -1
best_move = None
for index in range(0, len(moves)):
eval = self.eval_move(moves, index)
if eval > best_eval:
best_eval = eval
best_move = moves[index]
return best_move
Falls es nur einen einzigen gültigen Zug gibt, wird dieser zurück gegeben. Ansonsten werden alle gültigen Züge der Reihe nach durchsucht. Für jeden Zug wird eine Bewertung berechnet, und am Ende wird der Zug mit der höchsten Bewertung zurück gegeben.
Der von den Methoden eval_move und eval_by_search implementierte Algorithmus berechnet den bestmöglichen Ausgang unter der Annahme, dass beide Spieler versuchen, ihre eigene Bewertung zu maximieren.
Wenn wir nun eine Instanz der Klasse SearchingPlayer im Nim-Spiel gegen einen zufälligen Spieler antreten lassen, sollte in der Regel der zufällige Spieler verlieren. Hier ist eine entsprechende Beispielausgabe.
>>> alice = SearchingPlayer("Alice")
>>> bob = RandomPlayer("Bob")
>>> SimpleNim(alice, bob, 21).play()
21 matches, Alice's turn
20 matches, Bob's turn
17 matches, Alice's turn
16 matches, Bob's turn
13 matches, Alice's turn
12 matches, Bob's turn
11 matches, Alice's turn
9 matches, Bob's turn
7 matches, Alice's turn
5 matches, Bob's turn
4 matches, Alice's turn
1 matches, Bob's turn
0 matches, Alice won
Für größere Streichholzhaufen können wir beobachten, dass die Suche nach dem besten Zug sehr lange dauert.
Tiefenbeschränkte Suche im Spielbaum
Für komplexe Spiele ist es nicht praktikabel, den Spielbaum vollständig zu durchsuchen. Es ist daher üblich, Zugfolgen nicht bis zum Ende sondern nur bis zu einer bestimmten Tiefe im Baum zu verfolgen. Die Klasse LimitingPlayer definiert dazu ein Attribut limit für die maximale Anzahl von Verzweigungen, die bei einer durchsuchten Zugfolge durchlaufen werden dürfen.
class LimitingPlayer(SearchingPlayer):
def __init__(self, name, limit):
super().__init__(name)
self.limit = limit
# weitere Definitionen folgen
Um die Suchtiefe wie beschrieben zu beschränken, überschreiben wir die Methode should_stop wie folgt.
def should_stop(self):
return self.limit == 0 or super().should_stop()
Da die Suche nun möglicherweise bei einem Spiel abbricht, das noch nicht beendet ist, müssen wir die Methode eval_on_stop so anpassen, dass sie auch mit nicht beendeten Spielen zurecht kommt.
def eval_on_stop(self):
if self.game.has_ended():
return self.game.eval_on_end()
return random()
Falls das Spiel beendet ist, rufen wir die dafür ausgelegte Implementierung der Oberklasse auf und geben ihr Ergebnis zurück. Falls nicht, geben wir eine zufällige Bewertung zwischen Null und Eins zurück. Für Spiele, für die wir eine spezialisierte Bewertungsfunktion angeben können, können wir eine Unterklasse von LimitingPlayer definieren, in der wir die Methode eval_on_stop überschreiben.
Die Methoden make_move und undo_move überschreiben wir so, dass das Attribut limit manipuliert wird, wenn es Alternativen zum übergebenen Zug gibt.
def make_move(self, move, count):
super().make_move(move, count)
if count > 1:
self.limit = self.limit - 1
def undo_move(self, move, count):
super().undo_move(move, count)
if count > 1:
self.limit = self.limit + 1
Mit diesen Definitionen, implementieren die geerbten Methoden eval_move und eval_by_search die beschriebene tiefenbeschränkte Suche. Wir können damit eine weitere Simulation des Nim-Spiels starten.
>>> alice = LimitingPlayer("Alice", 10)
>>> bob = RandomPlayer("Bob")
>>> SimpleNim(alice, bob, 42).play()
42 matches, Alice's turn
41 matches, Bob's turn
38 matches, Alice's turn
35 matches, Bob's turn
34 matches, Alice's turn
33 matches, Bob's turn
30 matches, Alice's turn
29 matches, Bob's turn
26 matches, Alice's turn
23 matches, Bob's turn
21 matches, Alice's turn
18 matches, Bob's turn
17 matches, Alice's turn
16 matches, Bob's turn
14 matches, Alice's turn
13 matches, Bob's turn
10 matches, Alice's turn
9 matches, Bob's turn
7 matches, Alice's turn
5 matches, Bob's turn
2 matches, Alice's turn
1 matches, Bob's turn
0 matches, Alice won
Trotz der beschränkten Suchtiefe gelingt es Alice am Ende gegen den zufälligen Spieler Bob zu gewinnen.
Beschneidung des Spielbaums
Bei geschickter Protokollierung von Zwischenergebnissen, gibt es noch mehr Potential, die Suche im Spielbaum vorzeitig abzubrechen. Bei der Suche im Spielbaum speichern wir als Zwischenergebnis den Wert best_eval für die beste bisher gefundene Bewertung. Rekursive Aufrufe speichern entsprechende Werte für uns und den Gegner. Aus diesen Werten ergeben sich Grenzen für solche Bewertungen, die für die Suche interessant sind. Bewertungen, die unterhalb dem bisher gefundenen besten Wert liegen, sind uninteressant, weil sie weniger Erfolg versprechen als ein bereits gefundener Zug. Statt dem niedrigeren Wert können wir gefahrlos den bisher besten gefundenen Wert zurückgeben, ohne das Ergebnis der Suche zu beeinflussen, denn der beste Wert wird nur bei einem noch besseren Wert angepasst.
Interessanterweise lässt sich auch eine Obergrenze für interessante Bewertungen angeben. Bewertungen, die oberhalb der Obergrenze liegen, sind uninteressant, wenn der Gegner bereits eine Möglichkeit gefunden hat, uns eine niedrigere Bewertung aufzuzwingen. Die Obergrenze ergibt sich also aus der bisherigen besten Bewertung des Gegners. Sobald uns eine Zugmöglichkeit zur Verfügung steht, die die Obergrenze überschreitet, können wir die Suche abbrechen, weil wir davon ausgehen können, dass der Gegner den vorherigen Zug, der uns diese Möglichkeiten bescherte, nicht auswählen wird. Statt des größeren Wertes können wir gefahrlos die übergebene Obergrenze zurück liefern, ohne das Ergebnis der Suche zu verändern, weil der Gegner einen bisher gefundenen Wert nur anpasst, wenn er uns eine noch niedrigere Bewertung aufzwingen kann.
Die Klasse PruningPlayer überschreibt die Methoden eval_move und eval_by_search unter Verwendung zusätzlicher Parameter für die besprochenen Grenzen.
class PruningPlayer(LimitingPlayer):
def eval_move(self, moves, index, min, max):
self.make_move(moves[index], len(moves))
eval = 1 - self.eval_by_search(min, max)
self.undo_move(moves[index], len(moves))
return eval
def eval_by_search(self, min, max):
if self.should_stop():
return self.eval_on_stop()
moves = self.game.valid_moves()
best_eval = min
for index in range(0, len(moves)):
if best_eval >= max:
return best_eval
eval = self.eval_move(moves, index, 1 - max, 1 - best_eval)
if eval > best_eval:
best_eval = eval
return best_eval
# weitere Definition folgt
In der Definition von eval_move wurden die Parameter min und max hinzugefügt,
um sie an eval_by_search weiterreichen zu können.
Die Definition von eval_by_search enthält neben den zusätzlichen Parametern eine bedingte Rückgabeanweisung im Schleifenrumpf, die die Suche wie oben diskutiert vorzeitig beendet.
Im rekursiven Aufruf wird als Obergrenze für den Gegner die umgekehrte bisher beste eigene Bewertung übergeben. Analog dazu wird als Untergrenze die umgekehrte Obergrenze verwendet, die dem bisher besten gefundenen Zug des Gegners entspricht.
Die neue Implementierung von select_move unterscheidet sich von der ursprünglichen nur durch den Aufruf von eval_move mit zusätzlichen Argumenten.
def select_move(self):
moves = self.game.valid_moves()
if len(moves) == 1:
return moves[0]
best_eval = -1
best_move = None
for index in range(0, len(moves)):
eval = self.eval_move(moves, index, -1, 1 - best_eval)
if eval > best_eval:
best_eval = eval
best_move = moves[index]
return best_move
Als Bereichsgrenzen übergeben wir solche außerhalb der berechneten Bewertungen. Die Untergrenze ist so klein, dass sie durch den ersten gefundenen Zug angehoben wird. Die Obergrenze ist so groß, dass sie durch den ersten gefundenen Zug des Gegners abgesenkt wird.
Nach diesen Anpassungen liefert die neue Implementierung von select_move den gleichen Zug wie die ursprüngliche. Dabei werden weniger Zugfolgen betrachtet als mit der ursprünglichen Implementierung, weil Teile des Spielbaums, die das Ergebnis nicht beeinflussen, nicht durchlaufen werden. Instanzen der Klasse PruningPlayer verhalten sich also wie Instanzen von LimitingPlayer, berechnen ihren Zug aber schneller. Die Suche ist weiterhin tiefenbeschränkt, und spezialisierte Implementierungen von eval_on_stop können in Unterklassen definiert werden.
28.2.1 Aufgaben
Bonusaufgabe: Reversi-Spielstände bewerten
Das Spiel Reversi (bzw. Othello) ist in der Datei reversi.py implementiert. Neben den üblichen Methoden der Klasse Game stellt die Klasse Reversi die folgenden Attribute und Methoden bereit:
all_tilesspeichert die Felder des Spielbretts als Array von Zeichenketten der Länge eins zurück. Jede Zeichenkette enthält entweder ein Leerzeichen oder den Anfangsbuchstaben eines Spielernamens.count_discs(player, tiles)liefert die Anzahl der Spielsteine des übergebenen Spielers zurück. Dabei werden nur die übergebenen Felder durchsucht, die das selbe Format haben müssen wie der Wert vonall_tiles.
Definieren Sie eine Unterklasse ReversiPlayer von PruningPlayer, die die Methode eval_on_stop mit einer für Reversi spezialisierten Implementierung überschreibt. Falls Sie Reversi nicht kennen, folgen Sie dabei den folgenden Grundsätzen:
- Sowohl das Verhältnis der Spielsteine als auch das Verhältnis der Zugmöglichkeiten beider Spieler spielen bei Reversi eine wichtige Rolle. Zu Beginn des Spiels sind Zugmöglichkeiten wichtiger, zum Ende des Spiels Spielsteine.
- In den Ecken platzierte Steine können nicht umgedreht werden. Solchen Steinen sollte daher besondere Aufmerksamkeit gewidmet werden.
Können Sie eine Bewertungsfunktion angeben, die besser ist als die zufällige Standard-Implementierung, die Sie überschreiben?
28.3 Lösungen
28.3.1 Lösungen
Aufgabe: Interaktiven Spieler implementieren
class Human(Player):
def select_move(self):
moves = self.game.valid_moves()
choice = ""
while not choice.isnumeric() or len(moves) < int(choice):
print("Your choice: ", end="")
choice = input()
return moves[int(choice) - 1]
Aufgabe: Verallgemeinertes Nim-Spiel implementieren
class Nim(Game):
def __init__(self, player1, player2, counts):
super().__init__(player1, player2)
self.counts = counts
def has_ended(self):
for index in range(0, len(self.counts)):
if self.counts[index] > 0:
return False
return True
def winner(self):
return self.current_player
def make_move(self, move):
heap = move[0]
count = move[1]
self.counts[heap] = self.counts[heap] - count
def valid_moves(self):
moves = []
for heap in range(0, len(self.counts)):
for count in range(1, self.counts[heap] + 1):
moves.append([heap, count])
return moves
def __str__(self):
lines = []
lines.append(super().__str__())
min = 0
for index in range(0, len(self.counts)):
count = self.counts[index]
options = []
for number in range(min + 1, min + count + 1):
options.append(str(number))
lines.append(" ".join(options))
min = min + count
return "\n".join(lines)
Bonusaufgabe: Tic-Tac-Toe implementieren
class TicTacToe(Game):
def __init__(self, player1, player2):
super().__init__(player1, player2)
self.grid = [" "] * 9
def has_ended(self):
return not (" " in self.grid) or self.winner() != None
def lines(self):
result = []
for row in range(0, 3):
result.append(self.grid[3 * row : 3 * (row + 1)])
for col in range(0, 3):
result.append(
self.grid[col : col + 1]
+ self.grid[col + 3 : col + 4]
+ self.grid[col + 6 : col + 7]
)
result.append(self.grid[0:1] + self.grid[4:5] + self.grid[8:9])
result.append(self.grid[2:3] + self.grid[4:5] + self.grid[6:7])
return result
def winner(self):
current_char = str(self.current_player)[0]
waiting_char = str(self.waiting_player)[0]
if ([current_char] * 3) in self.lines():
return self.current_player
if ([waiting_char] * 3) in self.lines():
return self.waiting_player
return None
def make_move(self, move):
self.grid[move] = str(self.current_player)[0]
def undo_move(self, move):
self.grid[move] = " "
def valid_moves(self):
moves = []
for index in range(0, len(self.grid)):
if self.grid[index] == " ":
moves.append(index)
return moves
def __str__(self):
grid = self.grid + []
moves = self.valid_moves()
for index in range(0, len(moves)):
grid[moves[index]] = str(index + 1)
result = super().__str__() + "\n"
for row in range(0, 3):
for col in range(0, 3):
result = result + " " + grid[3 * row + col]
result = result + "\n"
return result
Bonusaufgabe: Reversi-Spielstände bewerten
Da bei Reversi eine zufällige Bewertungsfunktion in Kombination mit Spielbaumsuche erstaunlich gute Ergebnisse liefert, ist es gar nicht so leicht, eine bessere anzugeben. Die folgende Implementierung basiert auf den in der Aufgabenstellung genannten Kriterien.
def relative_eval(one, two):
total = one + two
if total == 0:
return 0.5
return one / total
class ReversiPlayer(PruningPlayer):
def count_discs_at(self, player, indices):
tiles = []
for index in range(0, len(indices)):
tiles.append(self.game.all_tiles[indices[index]])
return self.game.count_discs(player, tiles)
def eval_on_stop(self):
if self.game.has_ended():
return self.game.eval_on_end()
current_discs = self.game.count_discs(
self.game.current_player, self.game.all_tiles
)
waiting_discs = self.game.count_discs(
self.game.waiting_player, self.game.all_tiles
)
disc_eval = relative_eval(current_discs, waiting_discs)
current_moves = len(self.game.valid_moves())
self.game.next_turn()
waiting_moves = len(self.game.valid_moves())
self.game.next_turn()
move_eval = relative_eval(current_moves, waiting_moves)
progress = (current_discs + waiting_discs) / 64
disc_move_eval = progress * disc_eval + (1 - progress) * move_eval
corners = [0, 7, 56, 63]
current_corners = self.count_discs_at(self.game.current_player, corners)
waiting_corners = self.count_discs_at(self.game.waiting_player, corners)
corner_eval = relative_eval(current_corners, waiting_corners)
return (disc_move_eval + corner_eval) / 2
29. Neuronale Netze
29.1 Das Perzeptron
Als einfaches Beispiel für Maschinelles Lernen betrachten wir das Perzeptron. Das Perzeptron ist ein einziges Neuron, das Eingabesignale in ein Ausgabesignal transformiert. Die Eingabesignale können dabei Zahlen sein, die als verschiedene Merkmale zu klassifizierender Eingaben interpretiert werden. Die Ausgabe eines Perzeptrons ist Eins oder Null, je nachdem, ob die Eingabe als der zu erkennenden Kategorie zugehörig klassifiziert wird oder nicht.
Die Ausgabe eines Perzeptrons ergibt sich neben der Eingabe aus intern gespeicherten Werten, sogenannten Gewichten. Für jedes Eingabesignal gibt es dabei ein Gewicht. Zur Berechnung der Ausgabe wird die mit den gespeicherten Gewichten gewichtete Summe gebildet. Zusätzlich speichert das Perzeptron einen sogenannten Bias, der zur gewichteten Summe hinzuaddiert wird. Wenn die so gebildete Summe größer als Null ist, liefert das Perzeptron als Ausgabe eine Eins, wenn nicht ist die Ausgabe Null.
Der Algorithmus, mit dem ein Perzeptron lernt, Eingaben zu klassifizieren ist vergleichsweise einfach. Zu Beginn des Trainings können alle Gewichte und der Bias als Null oder auch mit kleinen zufälligen Zahlen initialisiert werden. Anschließend werden diese Werte anhand von Trainingsbeispielen verändert, die aus Eingabesignalen und einer erwarteten Ausgabe bestehen. Nach Verarbeitung einer zunehmenden Anzahl von Trainingsbeispielen lernt das Perzeptron immer besser die erlernten Eingaben gemäß der erwarteten Ausgabe zu klassifizieren und kann dann auch solche Eingaben klassifizieren, die nicht in den Trainigsbeispielen vorkommen.
Die Veränderung des Bias und der Gewichte erfolgt anhand des folgenden Algorithmus.
Für jedes Trainingsbeispiel:
- Berechne den Klassifizierungsfehler als Differenz aus tatsächlicher und erwarteter Ausgabe.
- Ziehe von jedem Gewicht das Produkt aus dem zugehörigen Eingabesignal mit dem Klassifizierungsfehler ab.
- Ziehe den Klassifizierungsfehler vom Bias ab.
Als Beispiel betrachten wir einen Schritt im Lernprozess eines frisch initialisierten Perzeptrons mit zwei Eingängen. Wenn beide Gewichte sowie der Bias mit Null initialisiert werden, liefert dieses Perzeptron unabhängig von der Eingabe eine Null am Augang, da die intern berechnete Summe gleich Null ist. Wir wollen nun das Perzeptron so trainieren, dass es eine Eins am Ausgang liefert, wenn beide Eingänge Eins sind. Dazu berechnen wir zunächst den Klassifizierungsfehler. Da die tatsächliche Ausgabe Null ist, die erwartete Ausgabe aber Eins, ist der Klassifizierungsfehler \(0-1\), also \(-1\). Von jedem Gewicht (beide sind vor dem Lernschritt Null) ziehen wir nun das Produkt aus dem zugehörigen Eingabesignal (beide sind Eins) und den Klassifizierungsfehler \(-1\) ab. Nach dem Lernschritt sind also beide Gewichte \(0 - 1 \cdot (-1)\), also \(1\). Anschließend ziehen wir den Klassifizierungsfehler vom Bias (der vor dem Lernschritt Null ist) ab und erhalten dabei \(0 - (-1)\), also ebenfalls \(1\). Nach diesem Lernschritt berechnet das Perzeptron mit zwei Einsen als Eingabe die Ausgabe \(1\), da die intern berechnete Summe \(1\cdot1 + 1\cdot1 + 1\), also größer als Null ist.
Um solche Berechnungen nicht länger von Hand ausführen zu müssen, wollen wir sie im folgenden programmieren.
Programmierung eines Perzeptrons
Wir können ein Perzeptron als Array darstellen, das die internen Gewichte sowie den Bias enthält. Die folgende Funktion create erzeugt ein so dargestelltes Perzeptron mit übergebener Anzahl an Eingabesignalen.
def create(input_count):
# last entry is bias
weights = [None] * (input_count + 1)
# initialize weights and bias
for i in range(0, len(weights)):
weights[i] = 0.0
return weights
Alle intern gespeicherten Gewichte werden als 0.0 initialisiert. Da zusätzlich zu den Gewichten für die Eingabesignale auch der Bias gespeichert wird, hat das erzeugte Array ein Element mehr als es Eingabesignale gibt. Der Aufruf create(2) liefert beispielsweise als Ergebnis [0.0, 0.0, 0.0].
Die Funktion output erwartet als ersten Parameter ein als Array dargestelltes Perzeptron, als zweiten Parameter ein dazu passendes Array von Eingabesignalen und berechnet anhand der oben diskutierten Vorschrift, die Ausgabe des übergebenen Perzeptrons für die übergebene Eingabe.
def output(weights, inputs):
sum = 0.0
# compute weighted sum of inputs
for i in range(0, len(inputs)):
sum = sum + weights[i] * inputs[i]
# add bias
sum = sum + weights[len(inputs)]
# compute output based on sum
if sum > 0:
return 1
else:
return 0
Zusätzlich zu den bisher eingeführten Programm-Konstrukten enthält diese Deklaration am Ende des Funktions-Rumpfes eine Bedingte Anweisung, die entsprechend der berechneten Summe den Rückgabewert 1 oder 0 spezifiziert. Der Aufruf output(create(2), [1,1]) liefert beispielsweise das Ergebnis 0 (wie alle Aufrufe mit einem frisch initialisierten Perzeptron).
Die Prozedur train erwartet als Parameter ein Perzeptron, ein Array von Eingabesignalen und eine erwartete Ausgabe. Sie passt die intern gespeicherten Gewichte und den Bias entsprechend der oben diskutierten Vorschrift an.
def train(weights, inputs, target):
# compute error
error = output(weights, inputs) - target
# adjust weights
for i in range(0, len(inputs)):
weights[i] = weights[i] - error * inputs[i]
# adjust bias
weights[len(inputs)] = weights[len(inputs)] - error
Die Prozedur train speichert zunächst den Klassifizierungsfehler in einer Variablen error, die dann verwendet wird, um die Gewichte und den Bias anzupassen. Wir können die Interaktive Python-Umgebung verwenden, um den Effekt der train-Prozedur zu testen.
>>> neuron = create(2)
>>> neuron
[0.0, 0.0, 0.0]
>>> train(neuron, [1,1], 1)
>>> neuron
[1.0, 1.0, 1.0]
Durch den Aufruf der Prozedur train werden die in neuron gespeicherten Gewichte verändert. Das gezeigte Beispiel vollzieht den Lernschritt nach, den wir oben bereits von Hand berechnet hatten.
Um ein Perzeptron mit mehreren Trainings-Beispielen zu trainieren, können wir jene in einem Array speichern. Hier ist ein Array mit vier Trainings-Beispielen, die jeweils als Hash-Map1 dargestellt sind.
training_data = [
{"inputs": [0, 0], "target": 0},
{"inputs": [0, 1], "target": 0},
{"inputs": [1, 0], "target": 0},
{"inputs": [1, 1], "target": 1},
]
Eine Hash-Map wird zwischen geschweiften Klammern notiert. Jedes sogenannte Feld der Hash-Map hat einen Namen, dem ein Wert zugeordnet ist. Hier haben Hash-Maps für Trainings-Beispiele jeweils zwei Felder, eins mit dem Namen inputs und eins mit dem Namen target. Die gezeigten Paare aus Eingaben und erwarteter Ausgabe sind die der logischen Und-Verknüpfung: Die Ausgabe soll Eins sein, wenn beide Eingaben Eins sind und ansonsten Null.
Die folgende Zählschleife durchläuft das Array mit Trainings-Beispielen und wendet dann die Prozedur train für jedes Beispiel auf ein vorher erzeugtes Perzeptron an.
neuron = create(2)
for i in range(0, len(training_data)):
example = training_data[i]
train(neuron, example["inputs"], example["target"])
Auf die in einer Hash-Map (hier in der Variable example gespeichert) enthaltenen Komponenten können wir mit Hilfe von deren Namen zwischen eckigen Klammern zugreifen, wobei wir den Namen einen Doppelpunkt voranstellen.
Da das frisch initialisierte Neuron für die drei ersten Beispiele keinen Klassifizierungsfehler aufweist, wirkt sich nur das letzte (von uns bereits zwei mal berechnete) Beispiel auf die intern gespeicherten Gewichte aus. Nach dem Durchlauf dieser Schleife hat das in der Variablen neuron gespeicherte Array mit internen Gewichten also den Wert [1.0, 1.0, 1.0]. Dieses Neuron liefert für alle Trainings-Beispiele die Ausgabe 1, in den drei ersten Fällen also nicht mehr die erwartete Ausgabe. In der Hoffnung, dass weiteres Training die Situation verbessert, können wir die gezeigte Trainings-Schleife mehrfach ausführen.
neuron = create(2)
for j in range(0,5):
for i in range(0, len(training_data)):
example = training_data[i]
train(neuron, example["inputs"], example["target"])
print(neuron)
In diesem Fall genügt es, das Perzeptron fünf mal hintereinander mit allen Trainings-Beispielen zu trainieren, damit für alle betrachteten Eingaben die erwartete Ausgabe erzeugt wird. Nach dem Ablauf dieser Schleife hat das in neuron gespeicherte Array den Wert [2.0, 1.0, -2.0]. Der erste Eingang wird also mit 2.0 gewichtet, der zweite mit 1.0 und der Bias ist -2.0.
Nach der Schleife wird der Wert der Variablen neuron im Terminal ausgegeben.
Aufgrund der einfachen Struktur eines Perzeptrons lässt sich nicht jede Klassifizierungsaufgabe mit einem einzigen Perzeptron lösen. Ein einfaches Beispiel, das von einem Perzeptron nicht erlernt werden kann, ist die Exklusive Oder-Verknüpfung (XOR). Die Kombination mehrerer Neuronen erlaubt es, komplexere Klassifizierungen (inklusive XOR) zu erlernen, wozu aber auch komplexere Trainingsmethoden erforderlich sind.
-
Hash-Maps können ähnlich wie Arrays verwendet werden, erlauben aber nicht nur Zahlen als Indizes sondern beliebige Werte als sogenannte Schlüssel. Sie werden in einem anderen Kapitel ausführlicher behandelt. ↩︎
29.1.1 Aufgaben
Aufgabe: Zufällige Initialisierung
Die Funktion random, die mit from random import random importiert werden kann, liefert eine zufällige Zahl zwischen Null und Eins zurück. Passen Sie die Funktion create so an, dass die intern gespeicherten Gewichte und der Bias statt mit Null unabhängig voneinander mit zufälligen Zahlen zwischen Null und Eins initialisiert werden.
Aufgabe: Gesamtfehler und Trainingsfortschritt
Wir haben das Perzeptron fünf mal trainiert, bis es für alle betrachteten Beispiele die erwartete Ausgabe lieferte. Im Allgemeinen ist vorab nicht klar, wie lange wir das Perzeptron trainieren müssen, bis es fehlerfrei klassifiziert.
Definieren Sie eine Funktion total_error, die als ersten Parameter ein als Array dargestelltes Perzeptron erwartet, als zweiten Parameter ein Array von Trainingsbeispielen, und als Ergebnis den über alle Trainings-Beispiele akkumulierten Fehler liefert. Berechnen Sie dazu die Summe der Quadrate der Klassifizierungsfehler aller Trainings-Beispiele.
Passen Sie die Trainings-Schleife so an, dass ein weiterer Durchlauf mit allen Trainings-Beispielen durchgeführt wird, solange der Gesamtfehler größer als Null ist.
Bonusaufgabe: Grafische Darstellung eines Perzeptron mit zwei Eingaben
Ein Perzeptron mit zwei Eingaben können wir grafisch darstellen, indem wir die Ausgaben in einem geeignete Eingabe-Raster abtasten. Wenn wir die Eingabe-Werte als Koordinaten in einem 2-dimensionalen Koordinatensystem auffassen, und uns für beide Koordinaten auf einige Werte zwischen Null und Eins beschränken, können wir entsprechende Ausgaben des Perzeptrons im Terminal darstellen. Das oben trainierte Perzeptron würde wie folgt dargestellt, wenn wir für die x- und y-Koordinaten jeweils die Eingabewerte 0.0, 0.1, … 1.0 abtasten.
0 0 0 0 0 0 1 1 1 1 1
0 0 0 0 0 0 1 1 1 1 1
0 0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0
Wir können erkennen, dass das Perzeptron diesen Teil des Koordinatensystems durch eine trennende Gerade so in zwei Bereiche aufteilt, dass für die trainierten Beispiele die richtige Ausgabe erzeugt wird. Dass es durchaus mehrere Geraden mit dieser Eigenschaft gibt, können Sie bei Tests mit einem zufällig initialisierten Perzeptron beobachten.
Definieren Sie eine Prozedur display2d, die ein Perzeptron mit zwei Eingaben wie beschrieben abtastet
und die gezeigte Darstellung im Terminal erzeugt.
29.1.2 Lösungen
Aufgabe: Zufällige Initialisierung
Die angepasste Definition der Funktion create verwendet die Funktion random,
um die intern gespeicherte Gewichte und den Bias zu initialisieren.
def create(input_count):
# last entry is bias
weights = [None] * (input_count + 1)
# initialize weights and bias
for i in range(0, len(weights)):
weights[i] = random()
return weights
Aufgabe: Gesamtfehler und Trainingsfortschritt
Die Funktion total_error berechnet den Gesamtfehler eines Perzeptrons für ein Array von Trianingsbeispielen
als Summe der Quadrate der Klassifizierungsfehler aller Trainingsbeispiele.
def total_error(weights, data):
sum = 0.0
# add squared errors
for i in range(0, len(data)):
example = data[i]
error = output(weights, example["inputs"]) - example["target"]
sum = sum + error * error
return sum
Wir können total_error verwenden, um so lange zu trianieren, bis kein Fehler mehr auftritt.
while total_error(neuron, training_data) > 0:
for i in range(0, len(training_data)):
example = training_data[i]
train(neuron, example["inputs"], example["target"])
Bonusaufgabe: Grafische Darstellung eines Perzeptron mit zwei Eingaben
def display2d(weights):
for row in range(0, 11):
y = (10 - row) / 10
for col in range(0, 11):
x = col / 10
out = output(weights, [x, y])
print(" " + str(out) + " ", end="")
print("")
29.2 Training vernetzter Neuronen
Der Algorithmus zum Training eines Perzeptrons verändert die intern gespeicherten Gewichte und den Bias in trickreicher Weise so, dass das Perzeptron schrittweise immer besser in der Lage ist, die erwarteten Ausgaben zu berechnen. Warum das funktioniert, haben wir bisher nicht geklärt. Im folgenden skizzieren wir, wie die intern gespeicherten Werte systematisch an Trainings-Beispiele angepasst werden können. Dabei werden wir auch eine Intuition entwickeln, die klärt, warum das Verfahren funktioniert.
Interessanter Weise können wir dieses Verfahren dann ebenfalls anwenden, um mehrere vernetzte Neuronen zu trainieren. Künstliche Neuronale Netze bestehen aus mehreren Schichten, deren Neuronen zwar nicht miteinander dafür aber mit allen Neuronen benachbarter Schichten verbunden sind.
Zur Berechnung einer Ausgabe werden zunächst alle Eingabesignale als Eingaben für alle Neuronen der ersten Schicht verwendet. Die Ausgaben dieser Neuronen werden dann als Eingaben der Neuronen der nächsten Schicht verwendet und so weiter. Die Ausgabe des Neuronalen Netzes ist dann die Ausgabe der letzten Schicht.
Anders als beim Perzeptron wird die Ausgabe anhand der für ein einzelnes Neuron berechneten Summe auf neue Art berechnet. Die bisher betrachtete Funktion lieferte Eins, wenn die Summe größer als Null war und sonst Null. Der Graph dieser Funktion ist eine Treppenstufe, die beim Argument Null von Null auf Eins springt. Stattdessen kann die Ausgabe mit einer überall differenzierbaren Funktion (wie z.B. der Sigmoidfunktion) berechnet werden, bei der der Wechsel zwischen Null und Eins fließend in Form einer S-Kurve verläuft, die sich den Grenzen Null und Eins annähert.
Durch Verwendung einer überall differenzierbaren Funktion zur Berechnung der Ausgabe eines Neurons wird auch die Funktion, die ein Neuron (und damit auch ein Neuronales Netz insgesamt) berechnet, überall differenzierbar. Diese Eigenschaft ist entscheidend für das im Folgenden skizzierte Trainings-Verfahren.
Gradienten-Abstiegs-Verfahren
Um einzelne Neuronen und später auch Neuronale Netze systematisch zu trainieren, müssen wir wissen, wie die intern gespeicherten Werte den Klassifizierungsfehler beeinflussen. Änderungen der gespeicherten Gewichte (und Bias-Werte) führen zu entsprechenden Änderungen des Fehlers. Interessant ist vor allem, in welche Richtung sich solche Änderungen auswirken. Unser Ziel ist es, die Gewichte in jedem Schritt so anzupassen, dass sich der Fehler verkleinert, bis er eine gewählte Grenze unterschreitet.
Den Klassifizierungsfehler eines Neuronalen Netzes können wir als Summe der Klassifizierungsfehler über alle Neuronen der letzten Schicht berechnen. Um auszurechnen, wie sich Änderungen des Bias und der Gewichte auf den Fehler auswirken, können wir partielle Ableitungen der Fehlerfunktion ausrechnen. Hierbei betrachten wir die Fehlerfunktion in Abhängigkeit des Bias und der Gewichte. Die Eingaben des Neurons sind durch das gegebene Trainingsbeispiel festgelegt.
Der Vektor dieser partiellen Ableitungen heißt Gradient. Er zeigt in die Richtung, in die die Fehlerfunktion am schnellsten ansteigt. Um den Bias und die Gewichte so anzupassen, dass sich der Fehler verkleinert, können wir also den Gradienten vom Bias-Gewichts-Vektor abziehen. Um Fluktuation durch zu große Änderungen zu vermeiden, kann der berechnete Gradient vor der Subtraktion mit einem verkleinernden Faktor multipliziert werden.
Backpropagation
Bei der sogenannten Backpropagation wird eine Abweichung der tatsächlichen von der erwarteten Ausgabe eines Neuronalen Netzes rückwärts durch das Netz propagiert, um die internen Gewichte aller Neuronen anzupassen.
Da ein Trainingsbeispiel nur für die letzte Schicht erwartete Ausgaben definiert, ist zunächst nicht klar, welchen Fehler wir beim Training innerer Schichten zugrunde legen müssen. Um zu verstehen, wie genau wir die Gewichte innerer Schichten anpassen müssen, um den Fehler zu verkleinern, werden wieder partielle Ableitungen betrachtet, diesmal aber für ein Neuron, dessen Ausgabe mit Neuronen einer weiteren Schicht verbunden ist. Die Ausgabe eines inneren Neurons beeinflusst dabei den Klassifizierungsfehler auf mehreren Wegen, nämlich durch alle Neuronen der nächsten Schicht.
Auf Basis der skizzierten Ideen, kann der Klassifizierungsfehler von der letzten zur ersten Schicht propagiert werden, um schrittweise die intern gespeicherten Gewichte und Bias-Werte entsprechender Neuronen anzupassen.
29.3 Programmierung Neuronaler Netze mit Keras
Bisher haben wir eine eigene Implementierung Neuronaler Netze angegeben, die helfen soll, deren grundlegende Funktionsweise zu vermitteln. Für die Praxis ist unsere Implementierung nicht geeignet. Keras ist eine Programmier-Schnittstelle, mit deren Hilfe sich Algorithmen zum Maschinellen Lernen inlusive Neuronaler Netze auf einer vielseitigen und effizienten Basis (wie TensorFlow) implementieren lassen. Im folgenden wollen wir Keras anhand von Beispiel-Programmen kennenlernen.
Logische XOR-Verknüpfung
Wir haben bereits gesehen, dass ein einzelnes Neuron nicht ausreicht, um die XOR-Verknüpfung auf zwei Eingängen zu lernen. Mit mehreren Neuronen ist das aber möglich. Bevor wir komplexere Funktionen lernen, implementieren wir dieses Beispiel in Keras.
Die folgenden Definitionen speichern wir in einer Datei xor.py. Die ersten Zeilen importieren benötigte Bibliotheken.
import numpy
import tensorflow.keras
import matplotlib.pyplot
Nun definieren wir die Struktur unseres Neuronalen Netzes. Wir verwenden zwei Neronen in der ersten Schicht und ein weiteres in der zweiten Schicht. In Keras können wir Neuronale Netze mit mehreren Schichten mit Hilfe von tensorflow.keras.models.Sequential definieren. tensorflow.keras.layers.Dense liefert eine Schicht, in der alle Neuronen mit allen vorherigen Neuronen verbunden sind. Wir können Schichten mit der Methode add einem Neuronalen Netzwerk hinzufügen.
network = tensorflow.keras.models.Sequential()
network.add(tensorflow.keras.layers.Dense(2, input_dim=2, activation="sigmoid"))
network.add(tensorflow.keras.layers.Dense(1, activation="sigmoid"))
Der ersten Schicht übergeben wir die Anzahl der Eingaben als zusätzlichen Parameter input_dim. Jede Schicht kann zudem eine unterschiedliche Aktivierungsfunktion übergeben bekommen, die für Neuronen dieser Schicht verwendet wird. Wir verwenden die Sigmoidfunktion. Ohne weitere Parameter werden die Neuronen standardmäßig mit zufälligen Gewichten initialisiert.
Bevor wir das erzeugte Netz trainieren können, müssen wir es mit der Methode compile darauf vorbereiten.
network.compile(loss="mean_squared_error", optimizer="sgd", metrics=["acc"])
Als Parameter übergeben wir den Namen einer Fehlerfunktion (hier wie zuvor basierend auf Fehlerquadraten) und einen Trainings-Algorithmus. Der Name sgd steht hier für stochastic gradient descent also das zuvor diskutierte Gradienten-Abstiegs-Verfahren. Der Parameter metrics erlaubt es, zusätzliche Metriken anzugeben, die während des Trainings berechnet werden sollen. Die Abkürzung acc steht hier für accuracy, den Anteil der Trainings-Beispiele für die das Netz das richtige Ergebnis liefert.
Training
Die Trainingsdaten erwartet Keras in Form von NumPy-Arrays. NumPy ist eine Numerik-Bibliothek für Python.
inputs = numpy.array([[0, 0], [0, 1], [1, 0], [1, 1]])
targets = numpy.array([0, 1, 1, 0])
Als Eingaben deklarieren wir ein mehrdimensionales Array inputs mit vier Einträgen von denen jeder zwei Eingaben der XOR-Funktion beschreibt. Das Array targets beschreibt die zu den Eingaben gehörigen erwarteten Ausgaben.
Nun können wir unser Netzwerk mit der fit-Methode trainieren.
training = network.fit(inputs, targets, epochs=20000, batch_size=1)
Der Parameter epochs beschreibt, wie oft die intern gespeicherten Gewichte aktualisiert werden sollen; batch_size gibt an, wieviele (zufällig ausgewählte) Trainings-Beispiele für eine solche Aktualisierung herangezogen werden.
Wir können nun das erstellte Programm im Terminal ausführen.
# python3 xor.py
...
4/4 [==============================] - 0s 746us/step - loss: 0.2493 - acc: 0.5000
Epoch 9781/20000
...
Es gibt während des Trainings Informationen zum Trainingsfortschritt aus. Die Angabe acc: 0.5000 zeigt an, dass das Netz für 50% (also 2 von 4) der Trainings-Beispiele das richtige Ergebnis liefert.
Wir erweitern nun das Programm so, dass es den Trainingsfortschritt auch grafisch darstellt. Dazu greifen wir auf das Objekt training zu, das von der fit-Methode zurückgeliefert wurde.
fig = matplotlib.pyplot.figure()
pic = fig.add_subplot(1,1,1)
pic.plot(training.history['loss'])
pic.plot(training.history['acc'])
pic.set_title('XOR training')
pic.legend(['loss','acc'], loc='upper left')
pic.set_xlabel('epoch')
pic.set_ylabel('metric')
fig.savefig('xor_training.png')
Wenn wir das erweiterte Programm ausführen, erzeugt es nach dem Training die folgende Grafik.

Der blau dargestellte Gesamtfehler (loss) nimmt kontinuierlich ab während der Anteil Trainingsbeispiele mit richtigem Ergebnis (acc) sprunghaft zunimmt und teilweise fluktuiert.
Auffällig ist, dass das Training sehr viele Schritte benötigt. Da Gewichte zufällig initialisiert und Trainingsbeispiele zufällig ausgewählt werden, führt jeder Programmlauf zu einem anderen Ergebnis. Nicht immer ist der Anteil korrekt klassifizierter Trainingsbeispiele am Ende bei 100%.
Um das Training zu beschleunigen können wir die Lernrate anpassen. Sie beschreibt, wie stark Gewichte in jedem Schritt angepasst werden. Die Standard-Implementierung des Gradienten-Abstiegs-Verfahrens verwendet eine Lernrate von 0.01. Um sie anzuheben, passen wir den Aufruf der compile-Methode wie folgt an.
sgd = tensorflow.keras.optimizers.SGD(learning_rate=0.5)
network.compile(loss="mean_squared_error", optimizer=sgd, metrics=["acc"])
Nun genügen oft schon 500 Schritte (statt den vorherigen 20000), um alle Testbeispiele korrekt zu klassifizieren, wie die folgende Grafik zeigt.

Bei zu hoher Lernrate kann es jedoch passieren, dass die Gewichte in jedem Schritt so stark verändert werden, dass kein Minimum für die Fehlerfunktion mehr gefunden wird.
Exkurs: NumPy-Arrays
Bevor wir ein komplexeres Beispiel behandeln, sehen wir uns NumPy-Arrays etwas genauer an. Wir haben bereits gesehen, dass wir Arrays mit der Funktion numpy.array erzeugen können.
>>> data = numpy.array([[0,0,0],[0,1,1],[1,0,1],[1,1,0]])
>>> print(data)
[[0 0 0]
[0 1 1]
[1 0 1]
[1 1 0]]
Darüber hinaus benötigen wir Methoden, die es erlauben, Teil-Arrays zu extrahieren. Dazu können wir zu extrahierende Bereiche mit einem Doppelpunkt zwischen eckigen Klammern notieren:
>>> print(data[1:3])
[[0 1 1]
[1 0 1]]
Die erste Zahl ist der Index, bei dem der extrahierte Teil beginnt. Die zweite Zahl ist der erste nicht mehr extrahierte Index. Negative Indizes erlauben es, Elemente vom Ende her abzuzählen. Wenn man eine oder beide Zahlen weglässt wird vom Anfang und/oder bis zum Ende extrahiert:
>>> print(data[1:-1])
[[0 1 1]
[1 0 1]]
>>> print(data[:])
[[0 0 0]
[0 1 1]
[1 0 1]
[1 1 0]]
Wir können mehrere Bereiche hintereinander notieren, um innerhalb mehrdimensionaler Arrays zu extrahieren. Der folgende Aufruf extrahiert alle Einträge des Arrays data, von jedem aber nur die ersten beiden Elemente (alle bis auf das letzte).
>>> print(data[:,:-1])
[[0 0]
[0 1]
[1 0]
[1 1]]
Dieses Array haben wir als Eingaben im Training der XOR-Funktion verwendet. Der folgende Aufruf extrahiert aus dem Array data die von uns für das Training der XOR-Funktion verwendeten erwarteten Ausgaben.
>>> print(data[:,-1])
[0 1 1 0]
Statt eines Bereiches können wir also auch einen einzigen Index (ohne Doppelpunkt) angeben.
Praxisbeispiel
Wir wollen nun ein Neuronales Netz trainieren, auf Basis gewisser Patientendaten vorherzusagen, ob bei zugehörigen Patienten innerhalb von fünf Jahren Diabetes ausgebrochen ist. Die CSV-Datei mit Patientendaten enthält neun Spalten. Was die ersten acht Spalten bedeuten, können Sie in der Beschreibung nachlesen. Die letzte Spalte gibt an, ob beim zugehörigen Patient innerhalb von fünf Jahren Diabetes ausgebrochen ist. Diese Spalte soll unser Neuronales Netz also auf Basis der ersten acht Spalten vorherzusagen lernen.
Zunächst lesen wir dazu die Daten aus der CSV-Datei in ein NumPy-Array ein.
import numpy
import tensorflow.keras
import matplotlib.pyplot
data = numpy.loadtxt('diabetes.csv', delimiter=',')
inputs = data[:,:-1]
targets = data[:,-1]
Nun erzeugen wir ein Neuronales Netz mit drei Schichten. Die erste Schicht hat zwölf Neuronen, die zweite acht und die letzte eines zur Ausgabe einer Null oder Eins.
network = tensorflow.keras.models.Sequential()
network.add(tensorflow.keras.layers.Dense(12, input_dim=8, activation='sigmoid'))
network.add(tensorflow.keras.layers.Dense(8, activation='sigmoid'))
network.add(tensorflow.keras.layers.Dense(1, activation='sigmoid'))
network.compile(loss='mean_squared_error', optimizer='sgd', metrics=['acc'])
Anders als bisher teilen wir die Datensätze nun in zwei Hälften. Die eine Hälfte wird für das Training verwendet wie bisher. Die andere Hälfte dient zur Kontrolle (validation) des trainierten Netzes und hat selbst keinen Einfluss auf die Gewichte. Über den Parameter validation_split teilen wir der fit-Methode mit, welcher (zufällige) Anteil der Daten für die Kontrolle verwendet werden soll.
training = network.fit(
inputs, targets, epochs=2000, batch_size=10,
validation_split=0.5
)
Diesmal verwenden wir in jedem Schritt zehn Trainingsbeispiele, um eine gemittelte Gewichts-Änderung zu bestimmen und führen insgesamt 2000 Anpassungen durch.
# python3 diabetes.py
...
Epoch 2000/2000
384/384 [==============================] - 0s 115us/step - loss: 0.1853 - acc: 0.7135 - val_loss: 0.2047 - val_acc: 0.6406
Wir können erkennen, dass bei den Kontrolldaten der Fehler größer und der Anteil korrekt klassifizierter Beispiele kleiner ist. Den Trainingsfortschritt stellen wir auch wieder grafisch dar. Diesmal erzeugen wir getrennte Kurven für die zum Training und die zur Kontrolle verwendeten Daten.
fig = matplotlib.pyplot.figure()
pic = fig.add_subplot(1,1,1)
pic.plot(training.history['loss'])
pic.plot(training.history['acc'])
pic.plot(training.history['val_loss'])
pic.plot(training.history['val_acc'])
pic.set_title('diabetes training')
pic.legend(['loss','acc','val_loss','val_acc'], loc='upper left')
pic.set_xlabel('epoch')
pic.set_ylabel('metric')
fig.savefig('diabetes_training.png')
Das erweiterte Programm erzeugt die folgende Grafik.

Wir können erkennen, dass der Anteil korrekt klassifizierter Kontrolldaten zwischen 750 und 1000 Schritten deutlich abnimmt, nachdem er vorher gemeinsam mit dem entsprechenden Anteil der Trianingsdaten zugenommen hatte. Diesen Effekt nennt man Überanpassung (overfitting). Das Neuronale Netz lernt dabei spezifische Eigenschaften der Trainingsdaten, die bei einer Klassifizierung anderer Daten nicht helfen sondern stören.
Trainings-Abbruch
Wir wollen nun das Programm so erweitern, dass das Training abgebrochen wird, sobald es Anzeichen für eine Überanpassung gibt. Statt des Anteils korrekt klassifizierter Kontrolldaten betrachten wir hierzu den zugehörigen Gesamtfehler, weil dieser weniger stark fluktuiert. Wir erweitern den Aufruf der fit-Methode um einen sogenannten Callback, der das Training abbricht, wenn sich der Gesamtfehler bei der Klassifizierung aller Kontrolldaten (val_loss für validation-set loss) 500 Schritte lang nicht mehr verringert.
stop = tensorflow.keras.callbacks.EarlyStopping(monitor="val_loss", patience=500)
training = network.fit(
inputs, targets, epochs=2000, batch_size=10,
validation_split=0.5, callbacks=[stop]
)
Das angepasste Programm bricht nach etwa 1300 Schritten ab und erzeugt die folgende Grafik.

Da das letztlich erzeugte Netz noch immer (wenn auch nicht mehr so stark) an die Trainingsdaten überangepasst ist, erweitern wir das Training um einen weiteren Callback. Wannimmer der Gesamtfehler der Kontrolldaten ein neues Minimum erreicht, speichern wir das aktuell trainierte Netz in einer Datei best.h5.
best = tensorflow.keras.callbacks.ModelCheckpoint(
"best.h5", monitor="val_loss", save_best_only=True
)
training = network.fit(
inputs, targets, epochs=2000, batch_size=10,
validation_split=0.5, callbacks=[stop,best]
)
Das beim Training gespeicherte Neuronale Netz können wir einlesen und auf alle Daten anwenden, um den korrekt klassifizierten Anteil aller Datensätze zu bestimmen. Das folgende Programm gibt den Gesamtfehler und den genannten Anteil aus.
import numpy
import tensorflow.keras
network = tensorflow.keras.models.load_model('best.h5')
data = numpy.loadtxt('diabetes.csv', delimiter=',')
print(network.evaluate(data[:,:-1], data[:,-1]))
Es erzeugt die folgende Ausgabe.
# python diabetes_eval.py
...
[0.20267222449183464, 0.671875]
Die erste Zahl ist der Fehler (loss) und die zweite der Anteil korrekt klassifizierter Daten (acc), der also gut 67% beträgt.
29.3.1 Aufgaben
Aufgabe: Eigene Experimente mit Keras
Experimentieren Sie im Programm zur Vorhersage von Diabetes mit alternativen Werten für die Parameter activation, loss und optimizer. Variieren Sie auch andere verwendete Parameter der Implementierung. Können Sie dadurch ein besseres Netzwerk zur Erkennung von Diabetes erzeugen?
29.3.2 Lösungen
Aufgabe: Eigene Experimente mit Keras
import numpy
import tensorflow.keras
import matplotlib.pyplot
data = numpy.loadtxt('diabetes.csv', delimiter=',')
inputs = data[:,:-1]
targets = data[:,-1]
network = tensorflow.keras.models.Sequential()
network.add(tensorflow.keras.layers.Dense(12, input_dim=8, activation='relu'))
network.add(tensorflow.keras.layers.Dense(8, activation='relu'))
network.add(tensorflow.keras.layers.Dense(1, activation='sigmoid'))
network.compile(loss='binary_crossentropy', optimizer='adam', metrics=['acc'])
stop = tensorflow.keras.callbacks.EarlyStopping(monitor='val_loss', patience=500)
best = tensorflow.keras.callbacks.ModelCheckpoint(
'best.h5', monitor='val_loss', save_best_only=True)
training = network.fit(
inputs, targets, epochs=5000, batch_size=10,
validation_split=0.3, callbacks=[stop,best]
)
fig = matplotlib.pyplot.figure()
pic = fig.add_subplot(1,1,1)
pic.plot(training.history['loss'][10:])
pic.plot(training.history['acc'][10:])
pic.plot(training.history['val_loss'][10:])
pic.plot(training.history['val_acc'][10:])
pic.set_title('diabetes training')
pic.legend(['loss','acc','val_loss','val_acc'], loc='upper left')
pic.set_xlabel('epoch')
pic.set_ylabel('metric')
fig.savefig('diabetes_training.png')

30. Relationale Datenbanken
31. Algorithmen und Datenstrukturen
31.1 Hashing
Wir haben bereits die Datenstruktur Dictionary in Python kennen gelernt und diese auch schon häufig verwendet. Sturkturen, wie Dictonaries werden auch als Map bezeichnet, da man in ihnen Schlüssel auf Werte abbildet. Wir haben auch schon mögliche Implementierungen diskutiert. Eine effiziente Implementierung ist z.B. als AVL-Suchbaum möglich.
In der Praxis verwendet man für solche Maps aber in der Regel eine Implementierung, die auf Arrays basiert, die sogenannte Hash-Map. Auch in Python sind Dictonaries tatsächlich als Hash-Maps implementiert, welche intern ein Array verwendet.
Die Idee der Implementierung ist dabei sehr einfach. Man verwendet ein Array, welches Platz bietet, die Werte aufzunehmen. Das Array habe dabei die Größe \(n\). In der Regel erlaubt man aber sehr viel mehr als \(n\) Schlüssel und muss sich überlegen, wie man die Schlüssel auf den Wertebreich 1 bis \(n\), also die im Array verfügbaren Indizes abbilden kann.
Wie wir schon bei Dictonaries gesehen haben, verwendet man als Schlüssel auch gerne andere Werte als Zahlen, z.B. Strings oder sogar (fast) beliebige Python-Werte. Um also einen beliebigen Schlüssel auf einen Index im Array abzubilden, verwendet man eine Hash-Funktion
$$hash : KeySet \rightarrow {0, \ldots, n}$$
Dann kann man den Index, an dem ein Schlüssel in der HashMap ablegen möchte, einfach durch Anwendung der Hash-Funktion auf den Schlüssel ermitteln und hier den Wert ablegen oder auch nachschlagen.
Wir betrachten ein kleines Beispiel, bei dem wir eine Liste der Größe 5 und als Hashfunktion die folgende Python-Funktion verwenden (wir beschränken uns hier auf String-Schlüssel):
def hash_code(key) :
code = 0
for c in str :
code = code ` ord(c)
return code % 5
Wir addieren also alle ASCII-Werte und rechnen abschließend modulo 5, um einen passenden Index zu erhalten.
Dann können wir unser Liste wie folgt nutzen, um neue Einträge zur HashMap hinzu zu fügen:
| Komando | Hashwert | Liste |
|---|---|---|
| insert(‘hi’,42) | 4 | [None,None,None,None,42] |
| insert(‘hallo’,55) | 3 | [None,None,None,55,42] |
| insert(‘hola’,73) | 0 | [73,None,None,55,42] |
| insert(’toll’,0) | 3 | [73,None,None,??,42] |
Im letzten Schritt bekommen wir aber ein Problem. Der Schlüssel 'toll' wird auf denselben Index abgebildet, wir der Schlüssel 'hallo'. Es gibt eine sogenannte Kollision und wir können es ist unklar, wie wir beide Werte hier ablegen sollen.
Als Lösung gibt es im Wesentlichen zwei Ansätze:
- man speichert in der Liste nicht nur einen Wert, sondern eine Liste von Werten
- man verwendet den nächsten freien Platz in der Liste
Wir verfolgen hier den ersten Ansatz. Der zweiten Ansatz soll als Übung realisiert werden.
Wenn man nun also anstelle der Werte eine Liste von möglichen Werten abspeichert, so ist es darüber hinaus notwendig, auch den wirklichen Schlüssel abzuspeichern, da wir Schlüssel mit demselben Hash-Wert nach dem Hashing ja nicht mehr unterscheiden können. Wir fügen also Listen von Tupeln ein und erhalten für obiges Beispiel:
| Komando | Hashwert | Liste |
|---|---|---|
| insert(‘hi’,42) | 4 | [[ |
| insert(‘hallo’,55) | 3 | [[ |
| insert(‘hola’,73) | 0 | [[(‘hola’,73)],[ |
| insert(’toll’,0) | 3 | [[(‘hola’,73)],[ |
Schlägt man nun den Schlüssel ’toll’ in der HashMap nach, so schaut man zunächst an dem Index, welcher sich durch Anwendung der Hash-Funktion ergibt (hier 3) und muss dann in der Liste an Index 3 noch den konkreten Schlüssel nachschlagen.
Bei den Listen, mit denen wir die Kollisionen auflösen, handelt es sich tatsächlich um Python-Listen und keine Arrays. Dass diese tatsächlich geeignet sind, werden wir in Abschnitt ~\ref{pythonlisten} verstehen. Es sind auch noch andere Strukturen (verkettete Listen oder Suchbäume möglich). Die Vor- und Nachteile werden wir noch diskutieren.
Die HashMap ist also dann besonders gut gefüllt, wenn es möglichst wenige Kollisionen gibt und entsprechend die Listen in der Hash-Liste möglichst kurz sind. Dies hängt aber insbesondere davon ab, wie gut die Hash-Funktion ist. Werden die gegebenen Schlüssel tatsächlich möglichst gleichverteilt auf alle verfügbaren Indizes abgebildet?
Die bisher gemachten Überlegungen können wir nun in einer Klasse HashMap recht einfach realisieren:
class HashMap :
def __init__(self) :
self.hash_list = []
for i in range(5) : # default size of HashMap
self.hash_list.append([])
self.size = 0 # Entries within HashMap
def insert(self,key,value) :
i = 0
l = self.hash_list[hash_code(key)]
while i < len(l) and l[i][0] != key : # search key in list
i = i ` 1
if i == len(l) : # new key
l.append((key,value))
self.size = self.size ` 1
self.__resize() # not defined yet
else : # key exists, update
list[i] = (key,value)
def lookup(self,key) :
list = self.hash_list[self.__hashcode(key)]
i = 0 # search key in list
while i < len(list) and list[0][0] != key :
i = i ` 1
if i == len(list) : # key not found
return None
else : # key found
return list[i][1]
Ein weiteres Problem der HashMap ist, dass immer mehr Kollisionen entstehen, je voller die HashMap wird. Ist die Anzahl der Einträge in der HashMap sehr viel größer als der verfügbare Platz, so bildet die HashMap letztlich nur noch einen konstanten Faktor im Vergleich zur Verwendung einer einfachen Liste von Schlüssel-Wert-Paaren. Deshalb ist es sinnvoll, die Hashliste zu vergrößern, wenn ein bestimmter Füllgrad erreicht ist. Dieser Schritt kostet natürlich zusätzliche Laufzeit. Wir werden diese im nächsten Abschnitt genauer analysieren, verfolgen hier aber zunächst die Idee, dass wir ab einem bestimmten Füllgrad die Listengröße verdoppeln. Da die Hash-Funktion als Bildbereich alle Indizes der Hash-Liste hat, müssen wir für alle Schlüssel-Werte-Paare in der HashMap eine Neuberechnung vornehmen und diese dann entsprechend übertragen.
Hierzu haben wir in der Definition von insert bereits einen Aufruf einer Methode __resize vorbereitet, welchen wir nun auch recht einfach realisieren können:
def __resize(self) :
old_space = len(self.hash_list)
if self.size / old_space > 0.7 : # maximal fill 70%
old_hash_list = self.hash_list
self.hash_list = []
new_space = old_space * 2
self.hash_list = []
for i in range(new_space) :
self.hash_list.append([])
self.size = 0 # insert will correct size again
for list in old_hash_list :
for k,v in list :
self.insert(k,v)
Wir haben in der Implementierung Kollisionen mittels einer unsortierten Liste aufgelöst. Alternativen wären hier verkette Listen, sortierte Listen, so dass man effizienter mittels binärer Suche nachschlagen kann oder auch AVL-Bäume. In der Praxis hofft man eine gute Hashfunktion zu haben, so dass die Listen nicht besonders lang werden und die lineare Laufzeit über diesen Listen vernachlässigt werden kann.
Dass das Verdoppeln der Hash-Listen-Größe bei einem zu hohen Füllgrad sinnvoll ist, werden wir im nächsten Kapitel sehen, bei dem wir uns auch damit beschäftigen, wie der Schritt von Arrays zu den dynamsichern Listen effizient realisiert werden kann.
31.2 Python-Listen
In diesem Kapitel wollen wir untersuchen, wie Listen in Python implementiert sind und welche Laufzeiten hierbei gewährleistet werden können. Hierbei geht es insbesondere um die dynamischer Veränderung ihrer Größe, welche ein sehr flexibles Programmieren mit Listen ermöglicht. Dennoch haben einige Listen-Operationen dennoch keine konstante Laufzeit und für das effiziente Programmieren mit Listen ist es wichtig, um welche Operationen es sich dabei handelt und wie man Listen einsetzen soll.
Python Listen stellen eine dynamische Weiterentwicklung von Arrays dar. Arrays wurden schon in den ersten Programmiersprachen als die Datenstruktur zur Speicherung mehrerer Werte angeboten und sind auch heute noch als eingebaute Datenstruktur in C, C+` und Java sehr wichtig. Ein Array hat dabei in der Regel eine feste Größe, welche bei der Konstruktion festgelegt wird. Die Werte im Array können dabei standardmäßig beim Anlegen vordefiniert werden (z.B. in Java) oder undefiniert sein, wie in C. Der Zugriff auf die Elemente erfolgt über einen Index, welche in der Regel von Null bis zur Größe des Arrays minus eins geht. Die Zugriffe (nachschlagen oder mutieren) sind hierbei in konstanter Zeit möglich und entsprechen in der Regel einem direkten Zugriff auf eine Speicherzelle im Speicher des Computers.
Arrays entsprechen also letztlich Python-Listen, ohne Operationen, die die Größe der Liste verändern. Auch Operationen, wie Slicen oder die Operation + zum Zusammenfügen von Listen standen zunächst für Arrays nicht zur Verfügung, können aber (insbesondere da sie die Liste nicht mutieren, sondern eine neue Liste konstruieren) auch für Arrays definiert werden. Problematisch ist allerdings, wenn Slices zum Verändern einer Liste genutzt werden und sich hierbei die Länge der Liste ändert. Auch dies kann nicht so einfach auf Arrays übertragen werden.
In Python gibt es keinen vordefinierten Array-Datentyp. Wir werden im Folgenden aber dennoch Arrays in Python verwenden und hierzu die Bibliothek numpy verwenden, welche spezielle Datenstrukturen für Arrays, aber auch Matrizen zur Verfügung stellt und im Bereich der numerischen Programmierung sehr beliebt ist. Die vordefinierten Funktionen auf den Arrays sind dabei sehr effizient in C implementiert und sehr umfangreich ausgestaltet, weshalb Python auch besonders gerne im Bereich Data Science und KI eingesetzt wird.
Wir demonstrieren die Verwednung von Arrays in numpy anhand des folgenden Beispielcodes:
import numpy
a = numpy.array([1,2,3,4,5])
print(a) # [1 2 3 4 5]
a[2] = 42
print(a) # [1 2 42 4 5]
print(a.size) # 5
print(a[4]) # 5
print(a+a) # [2 4 84 8 10]
b = numpy.zeros(5, dtype=int)
b[2] = 31
print(a+b) # [1 2 73 4 5]
In Zeile 3 legen wir eine neues Array an. Hierbei stellt die Funktion numpy.array einen Konstruktor des Array-Datentyps dar. Es erhält eine Liste als Parameter und legt ein Array an, welches genau die Werte der Liste enthält. Ein weitere Konstruktor ist zeros, welcher ein Array der übergebenen Größe (hier 5) anlegt und alle Werte mit 0 initialisiert. Hierbei legt numpy standardmäßig ein Array von Floatingpointzahlen an, welches wir durch Angabe des dtype auch auf int setzen können. Als Einschränkung dürfen Arrays in numpy aber nicht heterogen sein. Alle Werte müssen denselben Typ haben und es sind in der Regel Basistypen, die hier verwendet werden. Arrays können in numpy auch mehrdimensional sein, worauf wir hier aber nicht weiter eingehen.
Die weiteren Zugriffe auf das Array verhalten sich sehr ähnlich, wie bei Listen. Einzige Ausnahme ist die Operation +, welche die Arrays nicht konkateniert, sondern komponentenweise addiert, siehe Zeile 9 und 12. Hierbei wird aber keins der Arrays mutiert, sondern ein neues Array gleicher Größe angelegt.
Bei der Ausgabe werden Arrays zur besseren Unterscheidung zu Listen ohne Kommas dargestellt, was auch eher der Matrizen- oder Vektor-Schreibweise entspricht.
Methoden, wie append stehen zur Verfügung und Slices können nur sehr eingeschränkt verwendet werden, was hier dem Selbststudium überlassen werden soll.
Um zu verstehen, weshalb Operationen, die die Größe eines Arrays verändern problematisch sind, skizzieren wir kurz, wie Arrays im Speicher des Computers abgelegt werden. Sie beginnen an einer beliebigen Speicherstelle und enthalten hintereinander einfach die Werte, die im Array abgelegt wurden. Darüber hinaus wird in der Regel noch eine Information zur Größe des Arrays abgelegt, damit eine Fehlermeldung beim Zugriff auf einen Index außerhalb der Array-Größen erfolgen kann. Bei C ist dies nicht der Fall und man liest oder schreibt einfach irgendwo anders in den Speicher, was oft zu den berühmten Segmentation Faults führen kann.
Betrachtet man das Array aus Zeile 4 unseres Beispielprogramms, so wird dies wie folgt im Speicher abgelegt werden:
Adresse: |98|99|9A|9B|9C|9D|9E|9F|A0|
-------------------------------------
Wert : |B0|42|05|01|02|03|04|05|A4|
Hierbei ist in diesem Beispiel die Speicheradresse (welche wir vereinfacht als zweistellige Hexadezimalzahl betrachten) an der das Array abgelegt wurde 9A und die Werte stellen wir der Einfachheit halber ebenfalls als zweistellige Hexadezimalzahl dar. Die Werte des Arrays beginnen somit an Adress 9B und die Größe befindet sich in Adresse 9A. Die Adresse 9A wird in der Variablen a abgelegt, wie wir es auch vorher schon skizziert hatten (Variablen zeigen auf Objekte).
Greift man nun auf a[i] zu, wird der Index i+1 einfach zur Adresse in a hinzu addiert, was sehr effizient direkt über einen Ladebefehl des Prozessors möglich ist. Die zusätzliche 1 kompensiert hierbei die Längeninformation. Entsprechend kann auch ein mutieren eines Indexes durch eine einfache Schreiboperation in den Speicher sehr effizient realisiert werden.
Man beachte, dass der Speicher hinter dem Array wieder für andere Objekte verwendet wird. Möchte man das Array also vergrößern (z.B. mittels append) ergibt sich das Problem, dass hinter dem Array nicht wirklich Platz verfügbar ist und wir letztlich das Array nur an eine andere, freie Speicherstelle kopieren können. Hierzu bieten maschinennahe Programmiersprachen, wie C, in der Regel die Möglichkeit Speicher einer gewissen Größe anzufordern und diesen dann zu beschreiben. Möchte man also ein append realisieren, würde man also Speicher anfordern, der eine Speicherzelle größer ist, als der bisher für das Array verwendete und würde diesen das Array dann dort hin kopieren müssen, bevor man dann den angehängten wert hinzu fügt.
Diese Kopieroperation hat aber (auch in Maschinensprache) lineare Laufzeit in der Länge des Arrays, was die Operation vergleichsweise teuer macht und früher in der Regel in Form einer expliziten Programmierung in die Hände der Programmiererin gelegt wurde. Darüber hinaus gibt es noch ein weiteres Problem. Das Array liegt nach dem Kopieren natürlich an einer anderen Stelle im Speicher und wie wir ja wissen, kann es mehrere Referenzen auf dieses Array geben, z.B. wenn man eine weitere Variable auf dasselbe Array referenziert (b = a).
Referenzen zeigen ja nur in eine Richtung und wir speichern nicht alle Referenzen auf eine Array beim Array ab. Somit ist es nicht möglich, nach dem Vergrößern des Arrays in a, auch den Zeiger in b zu aktualisieren. Um es dennoch zu ermöglichen Objekte im Speicher zu verschieben, führt man eine sogenannte Box ein, welche einfach nur einen Zeiger auf das Array enthält und deren Speicheradresse wir dann in den Variablen a und b ablegen können. Diese Adresse wird niemals verändert und wir können nach dem Verschieben unseres Arrays einfach nur den Zeiger in der Box verändern und diese Änderung wird dann bei allen Verweisen auf unser Array sichtbar. In C werden solche Boxen in der Regel nicht verwendet und Objekte werden auch nicht im speicher verschoben. Dies ist natürlich effizienter, weshalb C auch als maschinennahe Programmiersprache bezeichnet wird. Höhere Programmiersprachen verwenden in der Regel solche Indirektionen, welche auch bei der automatischen Speicherverwaltung (Garbage Collection) sinnvoll sind, aber zu einem konstanten Slowdown führen.
Bei unserem obigen Beispiel haben wir die int-Werte direkt in die Speicherzellen geschrieben. Verwendet man heterogene Arrays, ist die Verwendung von Boxen für die Werte im Array ebenfalls sinnvoll, da es so möglich ist, auch größere Objekte (wie z.B. Listen) als einzelnen Eintrag im Array zu verwenden. In dem Array stecken also wieder nur Referenzen auf die entsprechenden Objekte, was wir auch vorher schon als Pfeile in den Objekt-Bildern dargestellt haben. Wenn man dies mit der Repräsentation von Variablen vergleicht, sieht man dass man Arrays auch als Hintereinanderreihung von Variablen auffassen kann und man mittels a[i] eben auf die i-te Variable im Array zugreift und diese lesen oder eben auch zuweisen kann.
Nachdem wir nun also verstanden haben, wie wir Arrays prinzipiell auch verlängern können, können wir unter Verwendung von numpy-Arrays eine eigene Implementierung von Listen entwickeln. Wir beschränken uns zunächst auf die Methoden zum Zugriff auf einen Index und die Methode append. Um eine Verwechslung mit den vordefinierten Listen zu vermeiden nennen wir unsere Klasse DynArray. Außerdem beschränken wir uns bei den Werten auf int-Werte, da Arrays in numpy nicht heterogen sein dürfen.
import numpy
class DynArray :
# construct an empty list, like []
def __init__(self) :
self.array = numpy.array([], dtype=int)
self.size = 0
# with this, you can access elements by l[index]
def __getitem__(self,index) :
return self.array[index]
# with this, you can modify indices by l[index] = value
def __setitem__(self,index,value) :
self.array[index] = value
# with this, you can compute the length by len(l)
def __len__(self) :
return self.size
# convert to string for output, like print(l)
def __str__(self) :
# for simplicity we use Pythons lists, but we could also
# produce the string directly
return str(list(self.array[0:self.size]))
Im Konstruktor initialisieren wir zunächst mit einem leeren Array (den Typ setzen wir sicherheitshalber auf int) und speichern auch die verwendete Größe.
Des weiteren definieren wir spezielle Methoden, welche uns wichtige Python-Funktionen für Listen zur Verfügung stellen. Wie __add__ wird z.B. die Mutation l[i] = v in einen Aufruf l.__getitem__(i,v) umgewandelt.
Nun wollen wir auch das append realisieren und müssen ein resize initiieren, welches neuen Speicher anlegt (durch das Anlegen des neuen Arrays) und dann (hier explizit) die Werte kopiert.
Wir werden das Array später nicht in jedem Schritt um nur eine Speicherzelle vergrößern, weshalb wir hier die neue Kapazität als Parameter übergeben.
def resize(self,new_capacity) :
old_array = self.array
self.array = numpy.zeros((new_capacity,),dtype = int)
for i in range(self.size) :
self.array[i] = old_array[i]
def append(self,x) :
if self.size == self.array.size :
self.resize(self.array.size ` 1)
self.array[self.size] = x
self.size = self.size ` 1
Bei der Verwendung des DynArray ergibt sich nun fast kein Unterschied mehr im Vergleich zur Python-Liste, was das folgende Testprogramm zeigt:
l = DynArray()
n = 10
for i in range(n) :
l.append(i)
print(len(l)) # 10
sum = 0
for x in l : # also works, without any further method definition
sum = sum ` x # simply iterates all indices
print(sum) # 45
Führt man dieses Programm (auch ohne die Summenberechnung) nun für unterschiedliche Werte in n aus, so sieht man, dass es nicht besonders effizient ist und die Laufzeit in \(O(n^2)\) liegt. Dies liegt daran, dass wir in jedem append-Aufruf das komplette Array kopieren und somit über den kleinen Gaus eine quadratische Laufzeit erhalten.
Es ist natürlich auch nicht sinnvoll, das Array in jedem Schritt um nur einen Eintrag zu vergrößern. Besser wäre es, hier auf Vorrat direkt 100 zusätzliche Zellen anzulegen. Hierdurch können dann die nächsten 99 append-Aufrufe ohne weiteres Kopieren erfolgen und einfach die freien Zellen im Array nutzen. Hierdurch verbessert sich die Laufzeit enorm. Allerdings behalten wir immer noch eine quadratische Laufzeit, da nun alle 100 Schritte ein Kopiervorgang durchgeführt werden muss und wir zwar nur noch in \(O(\frac{1}{100}n^2)\) liegen, was aber immer noch in \(O(n^2)\) ist. Die einzelne append Operation hat also eine Laufzeit von \(O(n)\).
Für die praktische Nutzung wäre es natürlich wünschenswert, wenn ein append-Aufruf konstante Laufzeit hätte und bisher haben wir Listen auch immer so verwendet, als würde dies gelten. Wir haben gesehen, dass eine Vergrößerung um einen größeren Wert zwar besser ist, aber eben nicht die Komplexität verändert. Wir müssen also dafür sorgen, dass für größere Listen, eine größere Vergrößerung erfolgt, als für kleinere Listen, um hier tatsächlich einen Effekt zu erzielen. Deshalb addieren wir beim Vergrößern keinen konstanten Wert, sondern verdoppeln die Arraygröße jeweils. Als kleines Detail sollten wir dann mit einem Array der Größe 1 starten, da sich sonst bei der Verdoppelung eine Größe von \(0 \cdot 2 = 0\) ergeben würde.
def append(self,x) :
if self.size == self.array.size :
self.resize(self.array.size ` 1)
...
Messen wir erneut die Laufzeiten unseres Programms, sehen wir, dass es sich nun linear verhält. Es scheint, dass das Programm in \(O(n)\) und die append-Funktion damit in \(O(1)\) liegt. Aber wie ist dies möglich. Wenn wir append analysieren, so hat die Funktion im Worst-Case eine Laufzeit von \O(n)\, mit \(n\) Größe des Arrays. Allerdings hat sie im Best-Case auch die Laufzeit \(O(1)\), wenn das Array eben nicht vergrößert und kopiert werden muss. Wieso spielt bei den Messungen die Worst-Case-Laufzeit von append letztlich keine Rolle?
Dies liegt daran, dass nach einem Worst-Case-Fall für ein Array der Länge \(l\) die Hälfte des neuen Arrays ungenutzt ist und als Konsequenz die nächsten \(l\) append-Operationen eine konstante Laufzeit haben. Erst danach findet erneut eine Operation mit \(2\cdot n\) Kopierschritten statt, bevor dann wieder \(2\cdot n\) Schritte lang der hinzugefügte Wert innerhalb des konstruierten Arrays und damit in konstanter Zeit abgelegt werden kann. Es ergibt sich also die folgende Situation für \(n\):
Das Array wird in den folgenden Schritten vergrößert:
$$ 1, 2, 4, 8, 16, 32, 64, \ldots$$
Betrachten wir also \(n\) append-Schritte, so ergibt sich, die folgenden Schritte des Algorithmus:
1 k ` 1 `
2 k ` 1 ` 1 +
4 k ` 1 ` 1 ` 1 ` 1 +
8 k ` 1 ` 1 ` 1 ` 1 ` 1 ` 1 ` 1 ` 1 +
...
= 1k ` 1 ` 2k ` 2 ` 4k ` 4 ` 8k ` 8 ` ...
= 1(k ` 1) ` 2(k ` 1) ` 4(k ` 1) ` 8(k ` 1) ` ...
wobei k die Kosten für das kopieren eines Arrays der Größe 1 ist und für eine Array der Größe \(n\) sich eben Kosten in Höhe von \(n \cdot k\) ergeben.
Summiert man also die Kosten für \(n\) append-Schritte, so ergeben sich Gesamtkosten in Höhe von
$$\ \ \ \sum\limits_{i=0}^{\lfloor\log_2 n\rfloor} 2^i \cdot (k 1)$$
$$ = (k+1) \cdot \sum\limits_{i=0}^{\lfloor\log_2 n\rfloor} 2^i$$
$$ = (k+1) \cdot 2^{\lfloor\log_2 n\rfloor 1} - 1$$
$$\leq (k+1) \cdot (n 2) - 1$$
$$ = (k+1) n 2k 2 - 1$$
$$ = (k+1) n 2k - 1$$
$$\in O(k\cdot n)$$
Gehen wir nun davon aus, dass \(k\) konstant ist (die Kosten für das anlegen eines Array-Platzes und das Kopieren eines Wertes), so ergibt sich, dass \(n\)-maliges Ausführen von append in \(O(n)\) ist. In der Regel wird \(k\) sogar 1 oder kleiner sein (ist in Python ja in C implementiert), so dass wir insgesamt eine Laufzeit von \(2n ` n - 1 = 3n - 1\) erhalten, also eine recht kleine Konstante.
Fasst man die Analyse noch einmal zusammen, so sieht man, dass für einen teuren Schritt (kopieren, linear in \(n\)) eben genau \(n\) günstige Operationen mit konstanter Laufzeit folgen. Man nennt dies eine \emph{amortisierte Laufzeit}, welche dann eben über viele Operationen gemittelt bedeutet, dass die einzelne Operation im Durchschnitt eben nur eine konstante Laufzeit hat.
Wichtig ist hierbei, dass die teuren Operationen immer seltener werden und damit eben immer mehr konstante Operationen folgen können, was wir durch eine Verdopplung und damit ein exponentielles Wachstum der Listengröße erreichen.
Man beachte hierbei aber, dass in einzelnen Situationen tatsächlich sehr viel Speicher ungenutzt verschwendet wird. Außerdem kann es immer noch passieren, dass einzelne append-Schritte eine längere Laufzeit haben, weshalb man in bestimmten zeitkritischen Anwendungen, wie z.B. im Bereich eingebetteter System mit amortisierten Laufzeiten vorsichtig sein muss. In den meisten Anwendungen spielt dies aber keine Rolle und die Listen in Python sind als solche dynamischen Arrays realisiert.
Neben append bieten Listen auch noch eine Methode pop, welche wir auch schon dazu genutzt haben, Listen als Stacks zu verwenden. Wir müssen also überlegen, wie wir die Arrays auch verkleinern können, um nicht unnötig Speicherplatz zu verschwenden. Hierbei macht es keinen Sinn, die Arrays direkt zu verkleinern, wenn sie nur noch halb gefüllt ist, da wir dann mit dem nächsten append-Schritt direkt wieder eine Verdoppelung der Arraygröße bewirken würden und wir so direkt mehrere teure Schritte hinter einander machen würden, was zu einer Worst-Case linearen Laufzeit in der aktuellen Listengröße von append und pop führen würde. Es macht also Sinn mit der Verkleinerung zu warten, bis das Array nur noch zu einem Viertel gefüllt ist und das Array dann zu halbieren. Dann haben wir für append wieder ausreichend Luft, bis das Array wieder verdoppelt werden muss und auch für weitere \(\frac{n}{4}\) viele pop-Schritte, bis das Array erneut halbiert werden kann. Werden also append- und pop-Schritte, wie beim Stack gemischt, wird die Laufzeit nur besser, da Größenänderungen des Arrays noch seltener stattfinden.
Mit dieser Strategie haben sowohl append als auch pop eine amortisierte, konstante Laufzeit und es ist somit möglich anstelle von Arrays nur die viel dynamischeren Listen zu verwenden. In Java ist man diesen Schritt nicht gegangen, sondern bietet weiterhin auch die statischen Arrays an. Die Klasse ArrayList bietet aber genau die vorgestellten dynamischen Arrays an und viele Programmierer verarbeiten lieber direkt diese, um später auch dynamische Erweiterungen machen zu können.
Die weiteren Methoden, wie extend oder auch das Ersetzen von Slices durch Listen andere Größe, haben aber auch in Python keine konstante Laufzeit. Dies sollte man bei der Programmierung beachten und diese Operationen immer mit Bedacht einsetzen. Oft ist der gewünschte Effekt aber auch auf anderem Weg nicht effizienter zu realisieren. Als Beispiel betrachten wir das Einfügen eines Wertes in eine Liste l[2:2] = [42], bei welchem sich die Listen zum einen Verlängert, aber die Listenelemente ab Index 3 aber eben auch alle um einen Index nach rechts geschoben werden müssen.
Bei der HashMap haben wir diese Idee, des Verdoppelns des Arrays auch schon umgesetzt und mit exakt der gleichen Argumentation erhalten wir hier ebenfalls eine amortisierte konstante Laufzeit für eine insert-Operation, unter der Annahme, dass wir eine gute Hashfunktion verwenden, welche wenig Kollisionen erzeugt.
31.3 Definition Suchbäume
Suchbäume sind binäre Bäume, deren Knoten mit Werten beschriftet sind. Darüber hinaus zeichnen sich Suchbäume dadurch aus, dass sie sortiert sind: Für jeden Knoten gilt, dass alle Werte im rechten Teilbaum größer und alle Werte im linken Teilbaum kleiner sind als sein Wert.
Hierbei ist es wichtig, dass dies für jeden Knoten im Suchbaum gilt.
Wir gehen zunächst davon aus, dass jeder Wert nur einmal im Suchbaum vorkommt, im Gegensatz zu den Listen, die wir sortiert haben und bei denen Werte mehrfach vorkommen durften.
Beispiele zu Suchbäumen
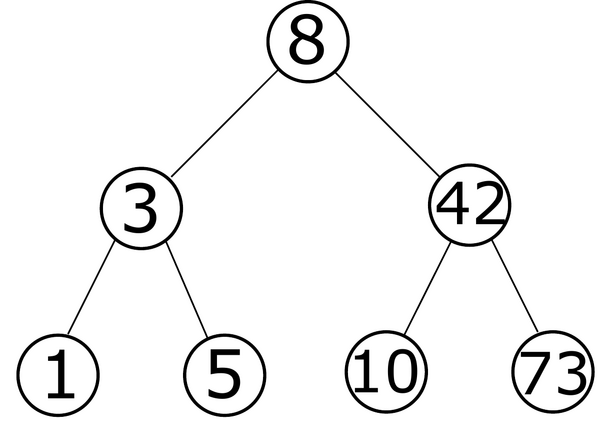
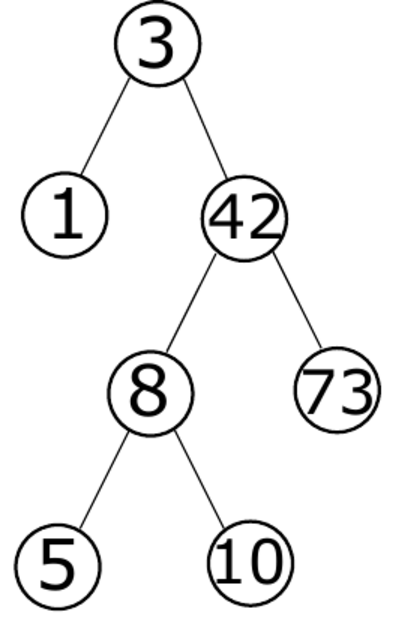
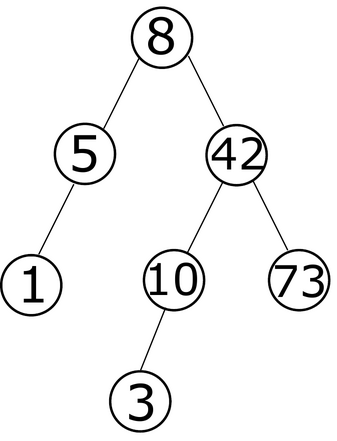
Der Binärbaum in Abbildung 30.3 ist kein Suchbaum, obwohl für jeden Knoten im Suchbaum gilt, dass sein linkes Kind kleiner und sein rechtes Kind größer als der Knoten ist. Der Fehler ist, dass die 3 im rechten Teilbaum der Wurzel vorkommt, aber kleiner als der Wert der Wurzel (8) ist. Korrigieren könnte man dies z.B. dadurch, dass man die 3 als rechten Kindknoten der 1 einfügt.
Suchen
Ein Suchbaum ist eine direkte Repräsentation für das Prinzip der binären Suche.
Jede Suche beginnt beim Wurzelknoten. Durch einen Größer/Kleiner/Gleich-Vergleich wird entschieden, ob es danach im rechten oder im linken Teilbaum weitergeht, oder ob der Wert bereits gefunden wurde.
Beispiel:
Im Suchbaum aus Beispiel 30.1 soll die 5 gesucht werden:
- Die 5 ist kleiner als die 8, also wird der linke Teilbaum gewählt.
- Die 5 ist größer als die 3, also wird der rechte Teilbaum gewählt.
- Die 5 ist gleich der 5, also wurde die 5 gefunden.
Das Suchen im Suchbaum funktioniert also genau wie die binäre Suche in einer Liste, mit dem Vorteil, dass der Index des nächsten Wertes nicht ausgerechnet werden muss, sondern direkt der nächste Kindknoten verwendet wird. Dabei ist es für die Laufzeit wichtig, dass der Baum einigermaßen ausgeglichen ist, also dass sich links und rechts ungefähr gleich viele Knoten befinden. Der folgende Baum zum Beispiel erfüllt alle Eigenschaften eines Suchbaums, eignet sich aber nicht zum schnellen Suchen:
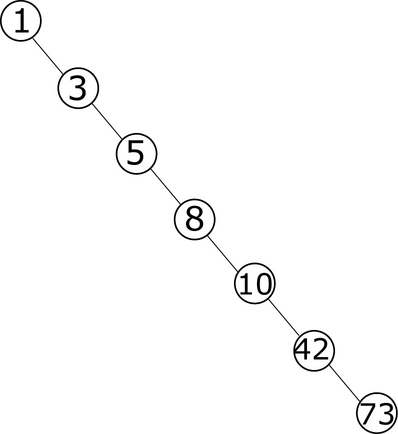
Wir gehen zunächst für die Laufzeitbetrachtungen davon aus, dass Suchbäume relativ ausgeglichen sind, ein solcher Fall also nicht auftritt. Tatsächlich kann man Suchbäume nach Einfüge- und Lösch-Operationen immer wieder geschickt umbalancieren, so dass sie ausgeglichen bleiben. Dies werden wir im nächsten Kapitel betrachten. Zunächst werden wir aber Prozeduren entwickeln, die das Suchen, Hinzufügen und Löschen eines Wertes in einem Suchbaum im Fall eines ausgeglichenen Suchbaums mit der Laufzeit \(\O(\log n)\) realisieren.
Einfügen
Zum Einfügen eines Wertes in einen Suchbaum muss zunächst mit der binären Suche die richtige Stelle gefunden werden. Sobald die Suche ins Leere läuft, kann der Wert genau an dieser Stelle als neues Blatt des Baumes eingefügt werden.
Beispiel:
Im Suchbaum aus Beispiel 30.1 soll die 30 eingefügt werden:
- Die 30 ist größer als die 8, also wird der rechte Teilbaum gewählt.
- Die 30 ist kleiner als die 42, also wird der linke Teilbaum gewählt.
- Die 30 ist größer als die 10, also wird der rechte Teilbaum gewählt.
- Der rechte Teilbaum ist leer, also kann die 30 hier eingefügt werden.
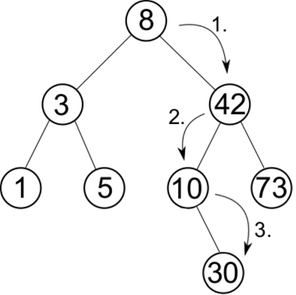
Jeder Knoten, der hinzugefügt wird, bietet durch die Binärstruktur des Baumes genau zwei neue Positionen, an denen wieder Blätter angehängt werden können. So ist sichergestellt, dass jeder beliebige Wert genau einen Platz hat, an dem er eingefügt werden kann. Genau wie bei einer Liste existieren immer \(n+1\) Positionen, an denen neue Werte eingefügt werden können, wobei \(n\) die Anzahl der schon vorhandenen Werte ist.
Man kann dies auch anders ausdrücken: Jeder Binärbaum mit \(n\) Knoten hat \(n+1\) nicht vorhandene Kindknoten.
Löschen
Soll ein Knoten aus dem Suchbaum gelöscht werden, so müssen wir sicherstellen, dass nach dem Löschen der Baum weiterhin zusammenhängend ist, d.h. es darf außer dem Wurzelknoten keinen Knoten ohne Elternknoten geben. Außerdem muss die Sortierung erhalten bleiben. Wir können unterschiedliche Fälle unterscheiden:
-
Blätter (also Knoten ohne Kindknoten) können einfach gelöscht werden.
-
Bei Knoten, die nur einen Kindknoten haben, kann dieser Kindknoten mit seinem kompletten nachfolgenden Teilbaum an die Stelle des zu löschenden Knotens gesetzt werden.
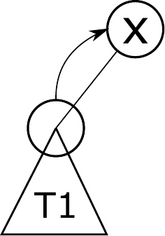
-
Zum Löschen von Knoten mit zwei Kindknoten gibt es im wesentlichen zwei Varianten:
-
Der Knoten mit dem größten Wert aus dem linken Teilbaum kann an die Stelle des gelöschten Knoten wandern, da er größer ist als alle Werte im linken Teilbaum und gleichzeitig kleiner als alle Werte im rechten Teilbaum. Dasselbe gilt natürlich auch für den Knoten mit dem kleinsten Wert des rechten Teilbaums.
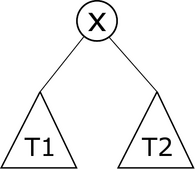
Beachte hierbei, dass der Knoten mit dem größten Wert im linken Teilbaum selber noch einen linken Teilbaum haben kann. Wenn man diesen also löscht, muss man Fall 2 für einen Knoten mit einem Kindknoten anwenden.
-
Eine andere Möglichkeit ist, den kompletten rechten Teilbaum als rechten Unterbaum an den rechtesten Knoten des linken Teilbaums zu hängen. Dann hat der zu löschende Knoten nur noch einen Kindknoten und kann wie in Fall 2 gelöscht werden.
-
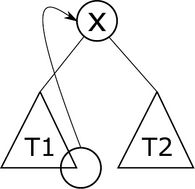
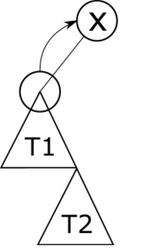
Implementierungen
Im Suchbaum hat eineinfügen in linken Teilbaum Knoten bis zu zwei Kindknoten. Dies stellt man in der Regel im Speicher etwas anders dar. Man unterscheidet zwei Arten von Knoten:
- innere Knoten, welche eine Beschriftung
vund exakt zwei Kindknotenlundrhaben:node(l,v,r) - Blätter, welche weder Beschriftung noch Kindknoten haben:
empty()
Einen Suchbaum mit den Werten 3 und 5 können wir dann wie folgt repräsentieren:
node(empty(),3,node(empty(),5,empty())
Konkret können wir die beiden Knoten repräsentieren als:
-
verschachtelte Liste:
Jeder Knoten wird durch eine Liste mit den drei Einträgen Wert, linkes Kind und rechtes Kind dargestellt. Die Einträge linkes Kind und rechtes Kind sind dann wieder dreielementige oder leere Listen. Diese Implementierung werden wir als nächstes realisieren.
-
verschachteltes Dictionary:
Jeder Knoten wird durch ein Dictionary mit den drei Einträgen Wert, linkes Kind und rechtes Kind dargestellt. Die Einträge linkes Kind und rechtes Kind sind dann wieder solche oder leere Dictionaries. Zur vollständigen Implementierung siehe Übung.
-
Klasse:
Jeder Knoten wird durch ein Objekt repräsentiert. Es enthält drei Attribute, zwei für die beiden Teilbäume und eins für den Wert.
Suchbäume als verschachtelte Listen
Suchbäume können in Python als verschachtelte Listen dargestellt werden. Alternativ kann man sehr ähnlich auch Tupel verwenden, was wir hier aber zunächst nicht weiter betrachten.
In unserer Implementierung stellen wir jeden Knoten, welcher einen Wert enthält, als Liste der Länge drei dar. Also auch die Blätter in unseren Suchbäumen, die eigentlich keine Kindknoten haben. Die Blätter in unserer Implementierung sind also vielmehr leere Listen, welche noch unterhalb der Blätter des Baumes verwendet werden. Hierdurch hat tatsächlich jeder Knoten im Binärbaum entweder zwei oder kein Kind.
Als Beispiel betrachten wir den folgenden Suchbaum:
Bild fehlt noch
Mit verschachtelten Listen würde er dann wie folgt repräsentiert:
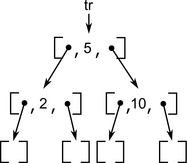
Um Binärbäume in dieser Form konstruieren zu können ist es sinnvoll zunächst einen Satz Hilfsfunktionen zu definieren, die uns helfen, solche Bäume zu konstruieren.
def node(l,v,r) :
return [l,v,r]
def empty() :
return []
Unter Verwendung dieser Funktionen können wir obigen Suchbaum konstruieren mittels
t = node(node(empty(),2,empty()),5,node(empty(),10,empty())
Da man mit diesen Funktionen also recht elegant Datenstrukturen konstruieren kann, nennt man solche Funktionen auch Smartkonstruktoren. Wie wir später sehen werden, verstecken Sie auch gewissermaßen die Implementierung, was dann auch durch passende Selektoren zum Selektieren der Kindbäume bzw. des Wertes und Testfunktionen zum Unterscheiden der beiden Knotentypen, elegant ergänzt werden kann:
# Selektoren
def left(l) :
return l[0]
def right(l) :
return l[2]
def value(l) :
return l[1]
# Testfunktion
def is_empty(tree) :
return tree == []
Die Verwendung unserer Hilfsfunktionen erleichtert nun die Realisierung der Funktion zum effizienten Suchen eines Wertes im Suchbaum:
def elem(v,tree) :
if is_empty(tree) :
return False
elif v < value(tree) :
return elem(v,left(tree))
elif v > value(tree) :
return elem(v,right(tree))
else :
return True # hier gilt v == value(tree)
Durch die Hilfsfunktionen sehen wir in der Implementierung der Funktion elem gar nicht mehr, wie genau wir den Suchbaum implementiert haben und produzieren sehr gut lesbaren Code.
Als nächsten Schritt wollen wir eine Prozedur add definieren, welche einen Wert zu einem Suchbaum hinzufügt. Unsere Implementierung wird dies mutierend realisieren, weshalb wir hier von einer Prozedur sprechen. Wir beginnen mit dem Absteigen, analog zur Implementierung von elem. Wir gehen ja davon aus, dass Werte nicht mehrfach in unseren Suchbäumen vorkommen. Sollte der Wert, den wir einfügen wollen also bereits im Baum vorhanden sein, können wir dies mit dem Rückgabewert False anzeigen. Waren wir erfolgreich liefert unsere Funktion `True+:
def add(v,tree) :
if is_empty(tree) :
??? # Einfuegen des neuen Knotens
return True
elif v < value(tree) :
return add(v,left(tree))
elif v > value(tree) :
return add(v,right(tree))
else :
return False # hier gilt v == value(tree)
An der Stelle ??? ist uns nicht klar, wie wir den neuen Knoten node(empty(),v,empty()) einfügen können.
Der übergeordnete Knoten verweist auf die leere Liste, an die die Variable tree nun gebunden ist.
In unserer Implementierung müssen wir diese Liste zu der Liste node(empty(),v,empty()) mutieren, damit der übergeordnete Knoten auf unseren neuen Knoten verweist.
Hierzu erweitern wir unsere Hilfsfunktionen um eine spezielle Mutationsfunktion
def empty_to_value(tree,v) :
if tree==[] :
tree.extend([empty(),v,empty()])
Hierbei ist die Funktion extend eine mutierende Methode der list Klasse, d.h. das vorhandene Listenobjekt bleibt erhalten, aber wird verändert (mutiert).
Mit dieser Funktion ist es dann möglich unsere Definition fertig zu stellen:
def add(v,tree) :
if is_empty(tree) :
empty_to_value(tree,v)
return True
elif v < value(tree) :
return add(v,left(tree))
elif v > value(tree) :
return add(v,right(tree))
else :
return False # hier gilt v == value(tree)
Dieser Einfügeschritt sähe dann für das Einfügen des Wertes 7 in den Suchbaum von oben wie folgt aus:
Bei allen Implementierungen (also auch mit Dictionaries, siehe Übung) ist es wichtig, dass das Einfügen eines neuen Wertes unbedingt als Mutation der bereits vorhandenen Objekte/Einträge geschieht, da der neue Eintrag sonst nicht mit seinem Elternknoten verbunden werden kann. Wenn man neue Einträge/Objekte verwenden will, muss man die Rekursion bereits eine Ebene höher beenden und den linken/rechten Kindknoten ersetzen. Dies ist aber in der Regel sehr viel aufwendiger, so dass es besser ist, leere Blätter zu verwenden, welche man in nicht-leere Knoten mutieren kann.
Wir haben nun einige Funktionen definiert, welche ein potentieller Nutzer unserer kleinen Bibliothek verwenden könnte. Hierbei ist es aber nur sinnvoll, dass ein Benutzer die Funktionen elem und add verwendet.
Außerdem könnte er noch empty zur Konstruktion eines leeren Suchbaums verwenden.
Von einer Verwendung der Funktion node sollte ein Benutzer aber absehen, da man mit ihr auch ungültige Suchbäume konstruieren kann. Wir verwenden die Funktion node lediglich, innerhalb unserer eigenen Definition.
Deshalb ist es sinnvoll eine klare Benutzerschnittstelle zur Verfügung zu stellen und hierzu ein Synonym für die Funktion empty zu definieren, welches für den Benutzer unserer Bibliothek gedacht ist:
# Konstruktor fuer den Benutzer
def empty_search_tree() :
return empty()
Damit stehen dem Benutzer nun drei Funktionen empty_search_tree, elem und add zur Verfügung.
In den Übungen kommt noch delete hinzu.
Das Abstraktionskonzept hinter dieser Aufteilung werden wir später noch bei der Betrachtung abstrakter Datentypen vertiefen.
Zum Abschluss des Kapitels beginnen wir noch mit einer Implementierung der Suchbäume mit Klassen.
Klassen geben uns die Möglichkeit Objekte mit Zustand zu definieren.
Die einzelnen Komponenten unserer Listen (linkes Kind, Wert und rechtes Kind) werden dabei Attribute des zugehörigen Objekts der Klasse.
Außerdem verwenden wir noch ein weiteres boolesches Attribut empty, welche uns zusätzlich anzeigt, ob der jeweilige Knoten leer ist (entspricht empty) oder nicht (node).
class SearchTree:
def __init__(self):
self.empty = True
self.value = None
self.left = None
self.right = None
def elem(self, value):
...
def add(self, value):
...
Der Konstruktor entspricht hier dem Anlegen eines leeren Suchbaums, also der Funktion empty.
Die Attribute left und right werden dann später auch andere Objekte der Klasse SearchTree enthalten, wodurch die Baumstruktur repräsentiert wird.
Verändert man diese Attribute entspricht dies genau der Mutation der leeren Liste in eine nichtleere Liste mit Hilfe der Funktion empty_to_value.
Die Methoden elem und add werden dann in den Übungen realisiert.