Darstellung von Algorithmen
Motivation
Wir haben bisher verschiedene Möglichkeiten kennengelernt, um Algorithmen zu beschreiben: Zum einen in natürlicher Sprache, die allerdings Uneindeutigkeiten enthalten kann und es erschwert, einen Algorithmus wirklich präzise und eindeutig zu beschreiben. Auf der anderen Seite haben wir die Umsetzung als Programm in einer konkreten Programmiersprache, also die Implementierung eines Algorithmus in Form von Programmcode. Diese Darstellung ist zwar maximal eindeutig, da ihre Syntax und Semantik durch die verwendete Programmiersprache genau vorgegeben sind, für Menschen aber nur dann verständlich, wenn die entsprechende Programmiersprache beherrscht wird. Zwischen diesen beiden Welten liegt der sogenannte Pseudocode, also eine Beschreibung in natürlicher Sprache, die sich aber auf ganz bestimmte Formulierungen und Anweisungen beschränkt – etwa “wiederhole … bis”, “falls … dann … sonst …” – so dass eine Beschreibung entsteht, die schon relativ nah am Code einer textuellen imperativen Programmiersprache ist, dabei aber allgemeiner verständlich ist.
Um einen Algorithmus zu einer gegebenen Problemstellung zu entwickeln und darüber zu kommunizieren, kann es hilfreich sein, den Ablauf zunächst auf Papier zu entwerfen, bevor er in Scratch oder einer anderen Programmiersprache umgesetzt wird. Als Alternative zu einer textuellen Beschreibung gibt es auch Möglichkeiten, Algorithmen unabhängig von einer konkreten Programmiersprache grafisch darzustellen. Zwei verbreitete Darstellungsformen dafür sind Struktogramme und Programmablaufpläne.
Diese grafischen Darstellungen sind sowohl für das Lesen von Algorithmen als auch für den Algorithmenentwurf hilfreich: Zum einen sind sie durch ihre reduzierte, strukturierte Darstellung übersichtlicher und eindeutiger als Texte – zum anderen leiten sie uns durch ihre formalen Vorgaben und die zur Verfügung stehenden grafischen Grundbausteine dazu an, uns beim Algorithmenentwurf auf bestimmte Ablaufstrukturen zu beschränken.
Struktogramme
Struktogramme (auch nach ihren Entwicklern Nassi-Shneiderman-Diagramme genannt) sind Diagramme zur grafischen Beschreibung von Algorithmen.1 In einem Struktogramm werden rechteckige Blöcke als Grundbausteine verwendet, die gestapelt und ineinander geschachtelt werden können.
| Anweisung | |
|---|---|
 |
Einzelne elementare Anweisungen werden jeweils durch einen einfachen Block dargestellt, der mit der möglichst kurz und präzise formulierten Anweisung beschriftet ist. |
 |
Anweisungen, die Unterprogramme aufrufen, können durch einen Block mit zwei Seitenstreifen dargestellt werden, um sie von elementaren Anweisungen zu unterscheiden (hier in Anlehnung an Unterprogrammaufrufe in Scratch rot schattiert). |
| Sequenz | |
|---|---|
 |
Blöcke können vertikal zu größeren Blöcken gestapelt werden, so dass sich Sequenzen ergeben. |
Für die Kontrollstrukturen (Fallunterscheidungen und Wiederholungen) gibt es spezielle Blöcke, in die andere Blöcke eingepackt werden.
| Wiederholung | |
|---|---|
 |
Der Block für eine bedingte Wiederholung besteht aus einem |
 |
Bei Endloswiederholungen wird in der Regel die Beschriftung weggelassen und der Rahmen |
| Fallunterscheidung | |
|---|---|
 |
Der Block für eine Fallunterscheidung (“falls … dann … sonst …”) besteht aus einer Kopfzeile, in der die Bedingung steht, gefolgt von zwei Blöcken, die nebeneinander stehen: Links der Block, der ausgeführt wird, wenn die Bedingung erfüllt ist, rechts der Block, der anderenfalls ausgeführt wird (beide Bereiche können auch leer sein). |
 |
Bei rein bedingten Anweisungen (“falls … dann” ohne “sonst”) bleibt der rechte Teilblock leer. |
Die Blöcke innerhalb von Wiederholungen und Fallunterscheidungen können dabei einfache Anweisungsblöcke, Sequenzen oder komplexere, aus anderen Blöcken zusammengesetzte Teilalgorithmen sein.
Ihnen ist vermutlich schon aufgefallen, dass Struktogramme den aus Scratch bekannten, ebenfalls aus Blöcken zusammengesetzten Skripten stark ähneln – mit dem Hauptunterschied, dass die alternativen Anweisungen einer Fallunterscheidung nebeneinander gestellt werden statt übereinander.2 Die folgende Tabelle stellt zur Veranschaulichung ein paar Struktogramm-Beispiele den jeweiligen Umsetzungen in Scratch gegenüber:
| Grundstruktur | Darstellung im Struktogramm | Darstellung in Scratch |
|---|---|---|
| Anweisungssequenz | 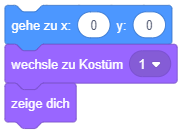 |
|
| Bedingte Wiederholung | 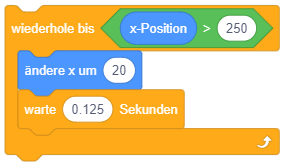 |
|
| Endloswiederholung | 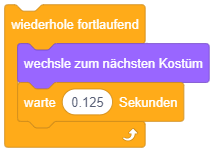 |
|
| Bedingte Anweisung (ohne Alternative) | 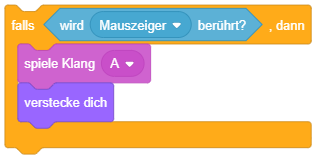 |
|
| Fallunterscheidung (Bedingte Anweisung mit Alternative) |
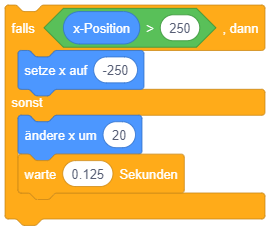 |
Beispiel: Code knacken
Betrachten wir noch einmal den einfachen Algorithmus zum Ermitteln der richtigen Kombination eines Zahlenschlosses aus dem vorigen Kapitel:
- Stelle Code
0000ein - Versuche Schloss zu öffnen
- Wiederhole bis Schloss offen ist:
- Stelle nächsten Code ein
- Versuche Schloss zu öffnen
Im Struktogramm wird der Algorithmus wie folgt dargestellt:
Die einzelnen Anweisungen werden durch entsprechend beschriftete Blöcke dargestellt, die gestapelt werden. Für die Wiederholung verwenden wir einen -förmigen Block, der mit der Wiederholungsbedingung “solange Schloss nicht offen ist” beschriftet ist und den Block der beiden zu wiederholenden Anweisungen enthält.
Varianten der Wiederholungen
Die Kontrollstruktur “Wiederholung” gibt es in verschiedenen Varianten, von denen wir ein paar bereits in Scratch kennengelernt haben: die Endloswiederholung, Wiederholung mit fester Anzahl und bedingte Wiederholung. An dieser Stelle werfen wir einen genaueren Blick auf diese verschiedenen Variante und grenzen sie voneinander ab.
Aus Scratch kennen wir die Endloswiederholung und die Wiederholung mit fester Anzahl (“wiederhole n-mal”) als Formen der Wiederholung ohne Bedingung.
Die aus Scratch bekannte bedingte Wiederholung ist eine Wiederholung mit Abbruchbedingung – sprachlich formuliert als “wiederhole bis Bedingung” – und wird folgendermaßen ausgeführt: Zuerst wird überprüft, ob die Bedingung erfüllt ist. Falls sie nicht erfüllt ist, wird der enthaltene Block einmal ausgeführt und anschließend erneut die Bedingung geprüft. Falls sie erfüllt ist, wird die Wiederholung beendet und das Programm fährt nach dem Wiederholungsblock fort.
Manchmal ist es aber intuitiver, eine Wiederholung stattdessen als “wiederhole solange Bedingung” zu formulieren. In diesem Fall erfüllt die Bedingung die Rolle einer Laufbedingung: Falls sie zu Beginn bzw. nach einem Durchlauf der Wiederholung erfüllt ist, wird ein weiterer Wiederholungsdurchlauf durchgeführt, anderenfalls wird die Wiederholung beendet (also genau entgegengesetzt zu einer Wiederholung mit Abbruchbedingung).3
Ein weiterer Unterschied besteht darin, ob die Lauf- oder Abbruchbedingung das erste Mal vor dem ersten Wiederholungsdurchlauf (bzw. zu Beginn einer Wiederholung) oder nach dem ersten Durchlauf (bzw. am Ende der Wiederholung) überprüft und ausgewertet wird. Bei den oben beschriebenen Varianten wird die Bedingung bereits zu Beginn einmal ausgewertet, weswegen sie im Block auch oben steht (im “Kopf” des Blocks). Diese Form der Wiederholung wird daher als kopfgesteuerte Wiederholung bezeichnet.
In Struktogrammen lassen sich auch fußgesteuerte Wiederholungen darstellen, bei denen die Bedingung nur am Ende jeden Durchlaufs geprüft wird – hier wird intuitiverweise ein -förmiger Block verwendet und die Bedingung ans Ende gestellt. Im Gegensatz zur kopfgesteuerten Wiederholung wird der enthaltende Block hier mindestens einmal ausgeführt, selbst wenn die Abbruchbedingung bereits zu Beginn erfüllt ist (bzw. die Laufbedingung bereits zu Beginn nicht erfüllt ist). Die kopfgesteuerte Wiederholung würde in diesem Fall gar nicht ausgeführt werden.
Die folgende Übersicht zeigt alle Varianten der Wiederholungen (kopf- oder fußgesteuert mit Lauf- oder Abbruchbedingung, Endloswiederholung und Wiederholung mit fester Anzahl), die sich in Struktogrammen darstellen lassen:
Für die bedingten Wiederholungen gilt: Ob kopf- oder fußgesteuerte Form, ob Lauf- oder Abbruchbedingung zur Formulierung eines Algorithmus am besten geeignet ist, hängt immer von der konkreten Situation ab. Manchmal kann eine der Varianten zu intuitiver verständlichen oder eleganter wirkenden Formulierungen führen. Es sollte allerdings beachtet werden, dass nicht alle Varianten in jeder Programmiersprachen direkt umsetzbar sind – in Scratch gibt es beispielsweise keine fußgesteuerten Wiederholungen – und daher bei der Implementierung eventuell umformuliert werden müssen.
Aufgabe: Geschirrspülmaschine leeren
Zur praktischen Veranschaulichung soll nun ein einfacher Algorithmus als Struktogramm entworfen werden. Als Problemstellung soll eine Geschirrspülmaschine ausgeräumt werden, die Tassen, Teller und Schüsseln enthält. Dabei sollen die verschiedenen Geschirrteile unterschiedlich behandelt werden:
Tassen sollen in den Schrank geräumt werden, alle anderen Geschirrteile ins Regal.
Geschirrteile, die beim Spülen kaputtgegangen sind, werden dagegen weggeworfen.
Dabei soll mitgezählt werden, wie viele Geschirrteile weggeworfen werfen.
Als Erstes legen wir fest, welche einfachen Anweisungen wir zur Formulierung des Lösungsverfahrens verwenden können, mit welchen Objekten gearbeitet wird und welche Eigenschaften der Objekte hier für uns relevant sind. Als problemspezifische Anweisungen reichen hier “nimm das nächste Teil aus der Spülmaschine”, “stelle das Teil in den Schrank”, “stelle das Teil ins Regal” oder “wirf das Teil weg”. Da wir außerdem zählen müssen, wie oft die Anweisung “wirf das Teil weg” ausgeführt wurde, verwenden wir zusätzlich eine Variable namens “Zähler” und als weitere Anweisungen Variablenzuweisungen wie “setze Zähler auf Wert” oder “erhöhe Zähler um Wert”.
Die naheliegenden Objekte, mit denen hier gearbeitet wird, sind hier die Geschirrteile, die wir aus der Spülmaschine nehmen. Uns interessieren nur zwei Attribute dieser Objekte: die Sorte (Tasse oder etwas anderes) und der Zustand (kaputt oder nicht). Außerdem müssen wir überprüfen können, ob die Spülmaschine leer ist oder nicht, um zu entscheiden, wann wir fertig sind.
Wir werden uns im Struktogramm also auf die folgenden elementaren Anweisungen, Variablenzuweisungen und Zustandsabfragen beschränken:
Nun geht es darum, die elementaren Anweisungen mit Hilfe von Kontrollstrukturen in den richtigen Ablauf zu bringen, wobei wir die Zustandsabfragen in den Bedingungen der Kontrollstrukturen verwenden werden.
Wir nähern uns Schritt für Schritt an die Lösung an, indem wir das Problem zunächst auf das Wesentliche reduzieren und Details wie das Zählen der weggeworfenen Geschirrteile erst einmal weglassen, um sie später zu unserer Lösung hinzuzufügen.
Wir beginnen also mit dem Grundgerüst: Es sollen nacheinander alle Geschirrteile aus der Spülmaschine genommen und verarbeitet werden, bis diese leer ist. Die Anweisung “nimm nächstes Teil” wird also innerhalb einer bedingten Wiederholung platziert. Als Abbruchbedingung wird geprüft, ob die Spülmaschine leer ist.
Wir ergänzen nun innerhalb des Blocks, der wiederholt ausgeführt wird, die eigentliche Verarbeitung der Geschirrteile. Es sollen unterschiedliche Aktionen durchgeführt werden, je nach Zustand und Sorte des zuletzt genommenen Objekts.
Als Erstes fügen wir also eine Fallunterscheidung zur Unterscheidung zwischen kaputten und nicht kaputten Objekten hinzu. Falls die Bedingung “ist kaputt?” erfüllt ist, soll die Anweisung “wirf weg” ausgeführt werden, die dazu in der linken Seite des Fallunterscheidungs-Blocks platziert wird.
In der rechten Seite des Fallunterscheidung-Blocks fügen wir nun den Block ein, der beschreibt, was im anderen Fall getan werden soll. Wenn das zuletzt genommene Objekt nicht kaputt ist, hängt es von seiner Sorte ab, was mit ihm gemacht werden soll.
Wir platzieren rechts also einen weiteren Fallunterscheidungs-Block, der als Bedingung prüft, ob das Objekt eine Tasse ist. Falls ja, soll die Anweisung “stelle in den Schrank” ausgeführt werden (links), anderenfalls die Anweisung “stelle ins Regal” (rechts).
Nun fehlt noch das Zählen der weggeworfenen Geschirrteile: Dazu ergänzen wir die Anweisung “erhöhe Zähler um 1” im linken Bereich der äußeren Fallunterscheidung, so dass sie zusätzlich zu “wirf weg” ausgeführt wird, wenn ein kaputtes Objekt aus der Spülmaschine genommen wurde. Der Vollständigkeit halber sollten wir den Zähler ganz zu Beginn noch auf 0 als Startwert setzen.
Das vollständige Struktogramm finden Sie unter “Schritt 4”. Es sind natürlich auch Variationen dieses Lösungsverfahrens möglich, z. B. könnten die Eigenschaften der Objekte auch in anderer Reihenfolge überprüft oder das Zählen der weggeworfenen Objekte auf andere Weise gelöst werden.
Fazit
Um einen Algorithmus als Struktogramm darzustellen, sind wir “gezwungen”, das Gesamtproblem in kleinere Teilprobleme zu zerlegen, bis nur noch Grundstrukturen wie Sequenzen und Kontrollstrukturen zur Lösung der Teilprobleme benötigt werden, die sich mit den Blöcken der Struktogramme darstellen lassen und zur Gesamtlösung zusammengebaut werden – ganz im Sinne der strukturierten Programmierung bzw. des “Computational Thinking”. Durch die Beschränkung auf diese einfachen Grundstrukturen lassen sich Algorithmen, die als Struktogramme formuliert werden, sogar in gewissem Maße automatisch in Programmcode verschiedener imperativer Programmiersprachen übersetzen.
Als Struktogramm formulierte Algorithmen lassen sich außerdem durch die Ähnlichkeit der Darstellung relativ einfach in Scratch implementieren – und andersherum Scratch-Programme sehr direkt als Struktogramme abstrakter skizzieren. Es kann also nützlich sein, Algorithmen, die später in Scratch umgesetzt werden sollen, zunächst auf Papier oder an der Tafel als Struktogramm zu entwickeln.
Struktogramme können mit Papier und Stift oder mit einem einfachen digitalen Zeichenwerkzeug wie LibreOffice Draw erstellt werden. Bequemer ist aber die Erstellung mit einem speziellen Struktogramm-Editor. Solche Tools sind oft auch in der Lage, automatisch Programmcode verschiedener Programmiersprachen aus dem erstellten Struktogramm zu erzeugen. Verweise auf Struktogramm-Editoren finden Sie in der Linksammlung bei den Software-Werkzeugen.
Programmablaufpläne
Programmablaufpläne (auch kurz “PAP”, engl. flowcharts) stellen eine weitere Möglichkeit zur grafischen Darstellung von Algorithmen dar, die sich deutlich von Struktogrammen unterscheidet. Hier werden Algorithmen als Graphen repräsentiert, die mögliche zeitliche Abfolgen von Anweisungen in einem Algorithmus abbilden. Die Knoten in diesem Graphen sind Anweisungen, Verzweigungen und Start-/Endzustände.
- Einzelne Anweisungen oder Unterprogrammaufrufe werden hier (wie bei Struktogrammen) durch Blöcke dargestellt, die mit der Anweisung beschriftet sind.
- Pfeile kennzeichnen den Übergang von einem Knoten zum nächsten. Ein Pfeil, der von einem Anweisungsblock ausgeht, gibt also beispielsweise an, mit welcher Anweisung als Nächstes fortgefahren wird.
- Verzweigungen werden durch Rauten dargestellt, die mit einer Bedingung beschriftet sind und von denen zwei Pfeile ausgehen. Sie repräsentieren Entscheidungen im Programmablauf, bei denen in Abhängigkeit von der angegebenen Bedingung entweder über den “ja”-Pfeil oder den “nein”-Pfeil fortgefahren wird.
- Start und Ende des Ablaufs werden durch kleine runde Knoten dargestellt. Jeder Algorithmus hat genau einen Startknoten, an dem der Ablauf beginnt.
Die folgende Tabelle stellt die grundlegenden Elemente dar, aus denen Programmablaufpläne bestehen:4
 |
 |
 |
 |
 |
| Start-/Endzustand | Anweisung | Unterprogrammaufruf | Übergang zum nächsten Element | Verzweigung |
Auffällig ist, dass es keine Grundbausteine für bedingte Anweisungen/Fallunterscheidungen oder bedingte Wiederholungen gibt wie bei Struktogrammen. Stattdessen werden diese Kontrollstrukturen alle mit Hilfe von Verzweigungen zusammengesetzt.
Der Ablauf eines Algorithmus kann für einen gegebenen PAP einfach nachvollzogen werden, indem vom Startknoten aus entlang der Pfeile gegangen wird und alle Anweisungen auf dem Weg ausgeführt werden. Bei jeder Verzweigung wird die in der Raute enthaltene Bedingung ausgewertet, um zu entscheiden, ob der mit “ja” beschriftete Pfeil oder der mit “nein” beschriftete Pfeil weiterverfolgt wird.
Damit ein Algorithmus, der als Programmablaufplan dargestellt wird, eindeutig ist, müssen ein paar Regeln eingehalten werden:
- Es muss genau einen Startknoten geben und mindestens einen Stopknoten.
- Von jedem Element des Programmablaufplans muss genau ein Pfeil ausgehen, der dieses Element mit dem als Nächstes auszuführenden Element verbindet. Einzige Ausnahmen sind Verzweigungen und Stopknoten.
- Von jeder Verzweigung gehen genau zwei Pfeile aus, von denen einer mit “ja” und der andere mit “nein” (oder “wahr” und “falsch”) beschriftet ist.
- Von Stopknoten gehen keine Pfeile aus, der Ablauf des Algorithmus endet hier also, da nicht weitergangen werden kann.
Mit diesen wenigen Elementen lassen sich alle bisher behandelten Kontrollstrukturen darstellen:
- Fallunterscheidungen bestehen aus einer Verzweigung, die den Ablauf in zwei parallele Abläufe aufteilt (der “wenn”-Fall und der “sonst”-Fall), die anschließend wieder zusammenführen.
- Wiederholungen entstehen, wenn Pfeile einen Kreis bilden. Üblicherweise muss hier am Beginn (bei einer kopfgesteuerten Wiederholung) oder am Ende (bei einer fußgesteuerten Wiederholung) dieses Kreises eine Verzweigung stehen, die es ermöglicht, in Abhängigkeit von einer Abbruchbedingung aus dem Kreis auszusteigen. Anderenfalls erhalten wir eine Endloswiederholung.
Die folgende Tabelle stellt die bekannten Kontrollstrukturen anhand von Beispielen als PAP dar und stellt sie zum Vergleich den jeweiligen Struktogrammen und Umsetzungen in Scratch gegenüber:
| Grundstruktur | Darstellung im PAP | Darstellung als Struktogramm | Darstellung in Scratch |
|---|---|---|---|
| Anweisungssequenz |  |
||
| Bedingte Wiederholung |  |
||
| Endloswiederholung |  |
||
| Bedingte Anweisung (ohne Alternative) |  |
||
| Fallunterscheidung (Bedingte Anweisung mit Alternative) |
 |
Beispiel: Code knacken
Auch hier soll als erstes Beispiel der einfache Algorithmus zum Ermitteln der richtigen Zahlenschloss-Kombination als Programmablaufplan untersucht werden:
Auf den Startknoten – den Beginn des Algorithmus – folgt eine Sequenz von zwei Anweisungen, die jeweils durch Pfeile miteinander verbunden sind. Anschließend folgt mit der bedingten Wiederholung der eigentlich interessante Teil: Hier wird eine Verzweigung verwendet, in der die Abbruchbedingung der Wiederholung “ist Schloss offen?” überprüft wird. Falls das der Fall ist, endet der Algorithmus: Der mit “ja” beschriftete Pfeil aus der Verzweigung wird also mit einem Stopknoten verbunden. Anderenfalls soll die Sequenz der beiden Anweisungen “stelle nächsten Code ein” und “versuche Schloss zu öffnen” ausgeführt werden. Der mit “nein” beschriftete Pfeil führt daher zur ersten dieser beiden Anweisungen und von dieser ein Pfeil zur nächsten. Nach der zweiten Anweisung soll erneut die Abbruchbedingung ausgewertet werden: Der von ihr ausgehende Pfeil führt daher wieder zur Verzweigung zurück.
Ablaufsimulation
Die folgenden Bilder stellen einen möglichen Ablauf dieses Algorithmus dar (die richtige Kombination lautet hier 0815):
Wir beginnen im Startknoten, der eindeutig festgelegt ist.
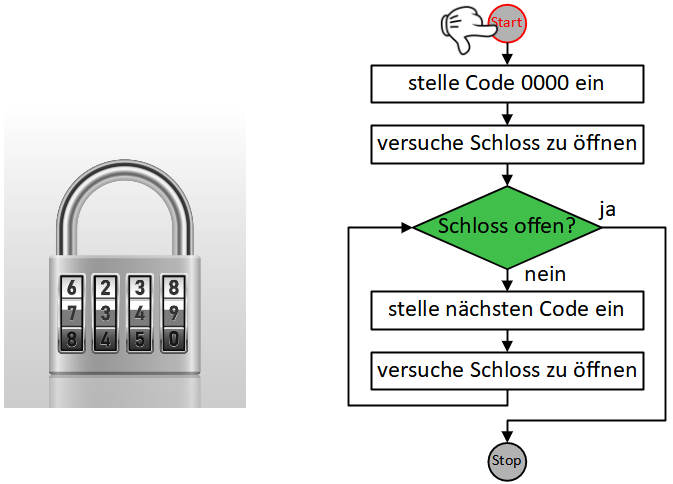
Vom Startknoten aus gehen wir entlang des Pfeils zur nächsten Anweisung und führen diese aus.
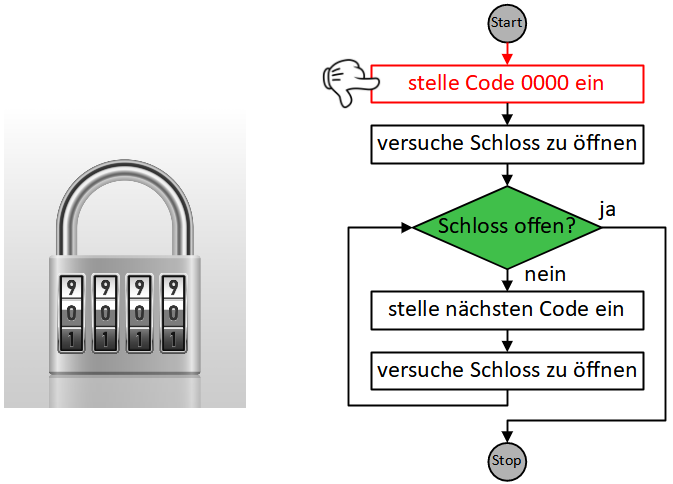
Von dieser Anweisung gehen wir wieder entlang des Pfeils zur Folgeanweisung und führen diese ebenfalls aus.
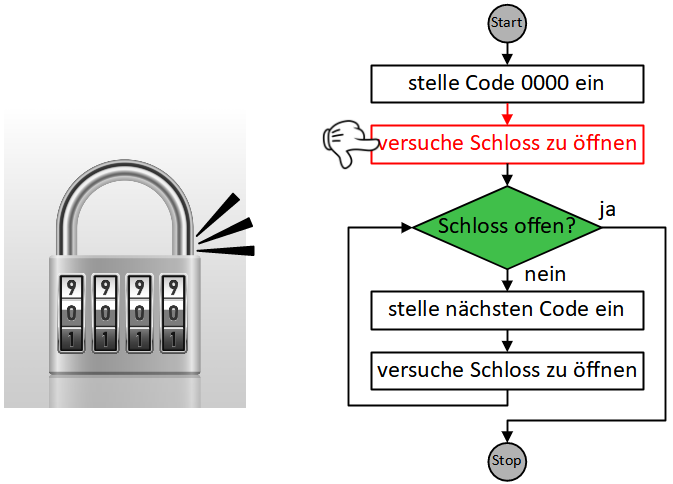
Wir erreichen eine Verzweigung: Nun wird die darin enthaltene Bedingung ausgewertet, die zu diesem Zeitpunkt nicht erfüllt ist.
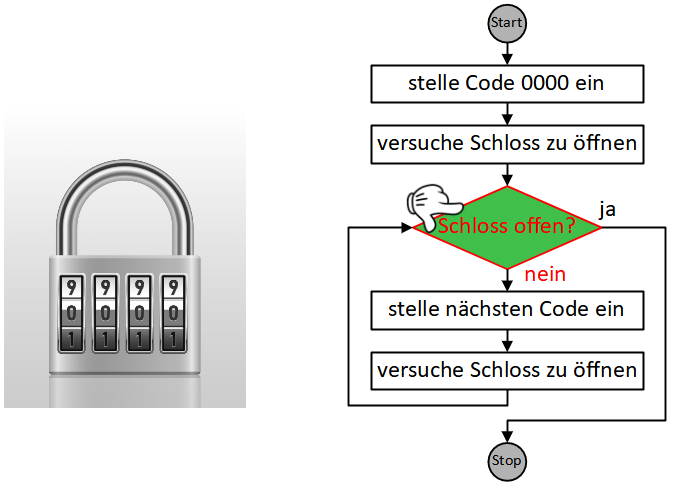
Also verfolgen wir den mit “nein” beschrifteten Pfeil zur nächsten Anweisung, die ausgeführt wird.
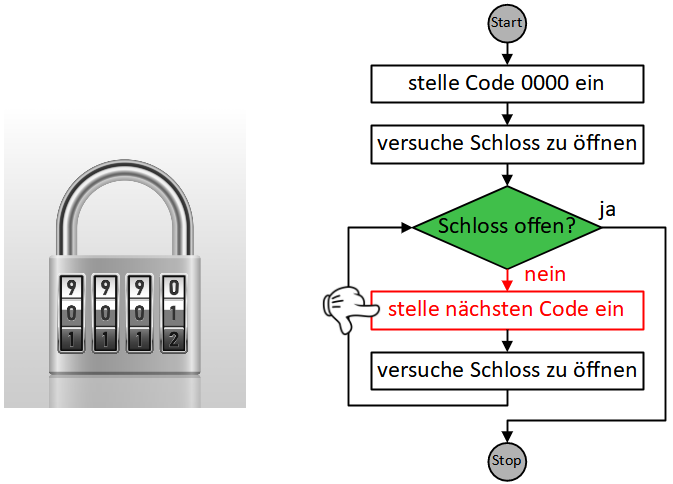
Von dieser Anweisung gehen wir wieder entlang des Pfeils zur Folgeanweisung und führen diese ebenfalls aus.
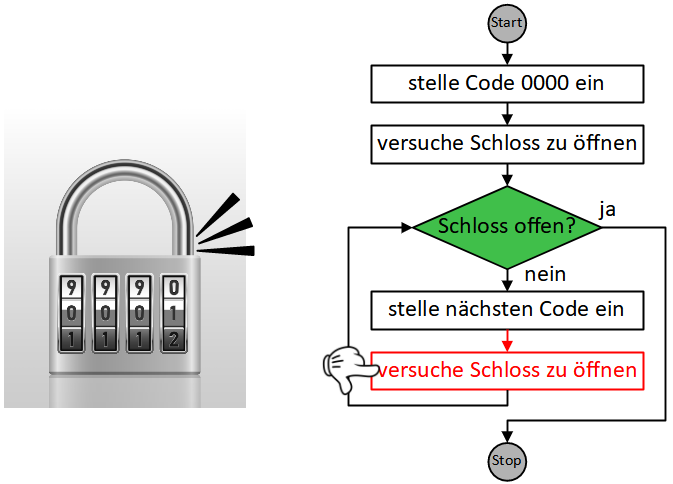
Über den Pfeil erreichen wir nun wieder die Verzweigung zu Beginn des Wiederholung und überprüfen ihre Bedingung erneut.
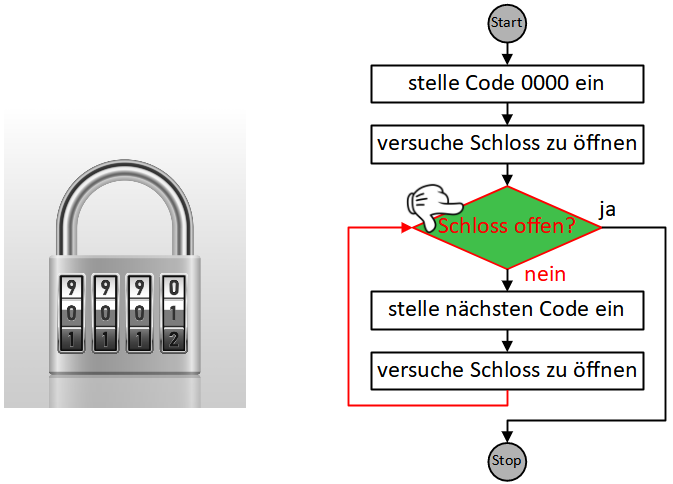
Es vergehen nun einige Schritte, bis wir im 2446. Schritt die Kombination 0814 erreichen und überprüfen.
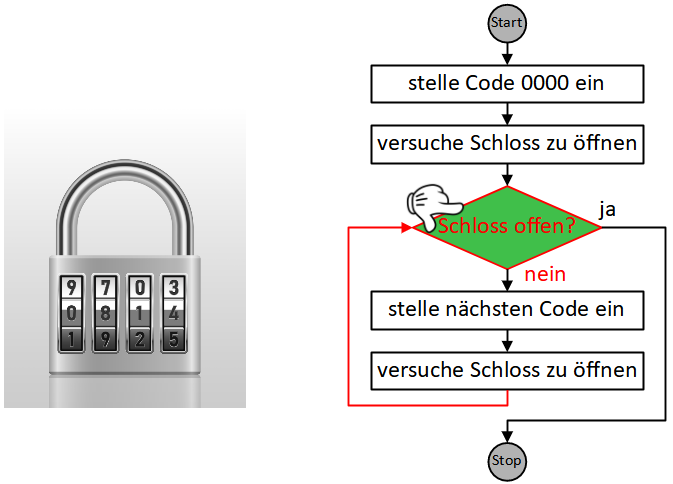
Da die Bedingung momentan nicht erfüllt ist wird entlang des “nein”-Pfeils gegangen und die nächste Anweisung ausgeführt.
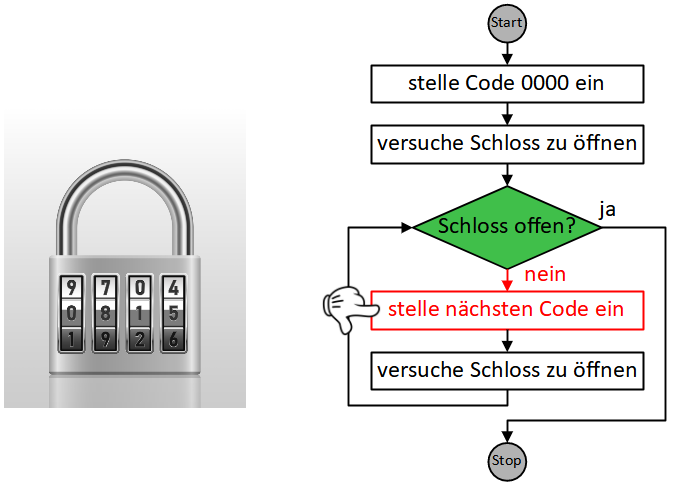
Die Ausführung der folgenden Anweisung öffnet das Schloss, da 0815 hier die richtige Kombination ist.
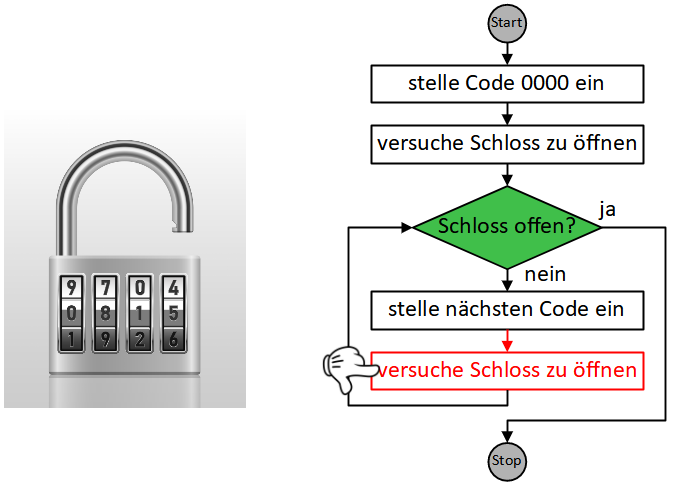
Wir kehren zur Verzweigung zu Beginn des Wiederholung zurück und überprüfen ihre Bedingung, die nun erfüllt ist.
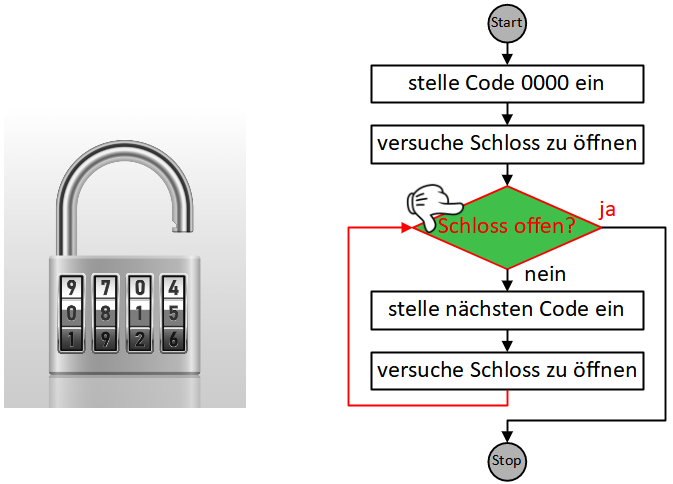
Also verfolgen wir den mit “ja” beschrifteten Pfeil und erreichen den Stopknoten. Der Algorithmus endet an dieser Stelle.
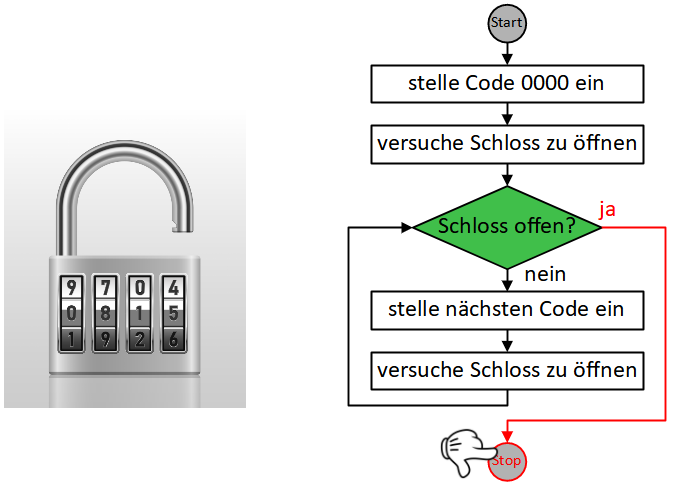
An diesem Beispielalgorithmus ist erkennbar, dass eine Wiederholung in einem PAP durch eine Verzweigung beschrieben wird, von der ein Weg ausgeht, der später wieder zu dieser Verzweigung zurückführt. Als Nächstes werden wir uns genauer ansehen, wie die verschiedenen üblichen Kontrollstrukturen in Programmablaufplänen umgesetzt werden.
Fallunterscheidungen im PAP
Bedingte Anweisungen und Fallunterscheidungen werden in Programmablaufplänen durch Verzweigungen umgesetzt, die zu zwei parallelen Wegen führen, die später wieder zusammenlaufen:
Bei einer bedingten Anweisung ohne Alternative enthält der Weg, von dem der “nein”-Pfeil ausgeht, keine weiteren Anweisungen:
Bei mehrfachen Fallunterscheidungen enthält dieser Weg dagegen weitere Verzweigungen in parallele Wege, die später mit dem “Hauptweg” zusammengeführt werden:
Wiederholungen im PAP
Generell werden Wiederholungen in Programmablaufplänen durch Verbindungen von Elementen mittels Pfeilen umgesetzt, die einen Weg bilden, der im Kreis läuft.
Bei bedingten Wiederholungen enthält dieser Kreis mindestens eine Verzweigung, die es ermöglicht, in Abhängigkeit von einer Abbruchbedingung aus dem Kreislauf auszubrechen:
Bei einer Wiederholung mit Laufbedingung (statt Abbruchbedingung) verläuft der Kreis vom “ja”-Pfeil aus, während der “nein”-Pfeil aus dem Kreis ausbricht:
Bei einer Endloswiederholung gibt es dagegen einen Weg ohne Verzweigung, der im Kreis führt:
Aufgabe: Geschirrspülmaschine leeren
Im Folgenden wird noch einmal der Algorithmus aus dem Beispiel Geschirrspülmaschine leeren betrachtet und Schritt für Schritt als Programmablaufplan formuliert. Dazu gehen wir von einem möglichen Ablauf des Algorithmus aus und untersuchen, welche Anweisungen nacheinander ausgeführt werden und welche Entscheidungen dabei gefällt werden müssen.
Als Erstes muss überprüft werden, ob die Spülmaschine leer ist, um zu entscheiden, was als Nächstes gemacht werden soll. Der Startknoten wird also durch einen Pfeil mit einer Verzweigung mit der Bedingung “Spülmaschine ist leer?” verbunden.
Falls die Bedingung erfüllt ist, sind wir fertig. Der “ja”-Pfeil der Verzweigung führt also zum Stopknoten. Anderenfalls soll das nächste Geschirrteil aus der Spülmaschine genommen werden.
Um zu entscheiden, was mit dem genommenen Geschirrteil gemacht werden soll, muss anschließend überprüft werden, ob das Teil kaputt ist oder nicht. Dazu wird eine weitere Verzweigung eingeführt, deren Bedingung in diesem Fall “Teil ist kaputt?” lautet.
Falls es kaputt ist, soll es weggeworfen werden und anschließend mit dem nächsten Geschirrteil (wenn vorhanden) weitergemacht werden. Dazu wird der “ja”-Pfeil der Verzweigung mit der Anweisung “wirf weg” verbunden, die wiederum zurück zur Verzweigung führt, in der geprüft wird, ob die Spülmaschine weitere Teile enthält.
Anderenfalls soll es entweder in den Schrank oder ins Regal gestellt werden, je nachdem, ob eine Tasse oder ein anderes Geschirrteil genommen wurde. Dazu wird eine weitere Verzweigung eingeführt, die als Bedingung “Teil ist Tasse?” prüft.
Tassen werden in den Schrank gestellt: Der “ja”-Pfeil der Verzweigung führt also zur Anweisung “stelle in Schrank”. Da anschließend mit dem nächsten Geschirrteil weitergemacht werden soll, führt der ausgehende Pfeil von dieser Anweisung zurück zur Verzweigung “Spülmaschine ist leer?”.
Andere Geschirrteile werden ins Regal gestellt: Der “nein”-Pfeil der Verzweigung führt also zur Anweisung “stelle ins Regal”. Auch diese Anweisung verweist anschließend zurück zur Verzweigung “Spülmaschine ist leer?”.
Abschließend müssen noch die Anweisungen zum Zählen der weggeworfenen Geschirrteile ergänzt werden: Zu Beginn (zwischen Startknoten und erster Verzweigung) wird der Zähler auf den Startwert 0 gesetzt und direkt nach dem Wegwerfen eines Geschirrteils um 1 erhöht.
Den vollständigen Programmablaufplan finden Sie unter “Schritt 8”. Wie beim Entwurf des Struktogramms sind auch hier andere Abläufe möglich.
Fazit
Anhand von Programmablaufplänen lässt sich die Ausführung von Algorithmen intuitiver nachvollziehen als bei Struktogrammen. Sie verfolgen einen anderen Ansatz beim Entwurf von Algorithmen, da hier vom Ablauf ausgegangen wird statt von der Struktur des Algorithmus. Allerdings erfordert der Entwurf von Algorithmen mit PAP eine gewisse Disziplin: Umfangreichere Algorithmen können schnell chaotisch und unübersichtlich werden und es können leicht uneindeutige Diagramme entstehen, wenn Kanten fehlen oder zu viele Kanten eingezeichnet werden.
Ein Problem von Programmablaufplänen ist, dass hier mit Sprüngen gearbeitet wird: Der Kontrollfluss kann von jeder Anweisung zu jeder beliebigen anderen Anweisung übergehen. Dadurch lassen sich Abläufe darstellen, die mit den üblichen Kontrollstrukturen gar nicht direkt beschreibbar sind und sich auch nicht in jeder Programmiersprache implementieren lassen.5 In Struktogrammen sind die möglichen Abläufe dagegen auf die üblichen Kontrollstrukturen eingeschränkt.
-
Die Elemente von Nassi-Shneiderman-Diagrammen sind in Deutschland genormt in DIN 66261. ↩︎
-
Tatsächlich sind blockbasierte visuelle Programmiersprachen wie Scratch, Snap! oder Blockly unübersehbar von Struktogrammen zur grafischen Darstellung von Algorithmen als Vorbild inspiriert. ↩︎
-
Jede Wiederholung mit Laufbedingung kann in eine Wiederholung mit Abbruchbedingung umformuliert werden und umgekehrt, indem die Lauf- bzw. Abbruchbedingung einfach negiert wird – z. B. ist “wiederhole bis Ziel erreicht” gleichbedeutend mit “wiederhole solange Ziel nicht erreicht”. ↩︎
-
Die grafischen Elemente von Programmablaufplänen sind genormt in DIN 66011, gemeinsam mit den ähnlichen Elementen von Datenflussplänen. ↩︎
-
Um Programmablaufpläne uneingeschränkt in einer Programmiersprache implementieren zu können werden sogenannte Sprunganweisungen benötigt, die es erlauben, den Kontrollfluss an einer beliebigen anderen Stelle im Programm fortzusetzen. Sprunganweisungen gelten in der imperativen Programmierung aber als tendenziell fehleranfällig, da sie dazu verleiten, unübersichtlichen und schwer überprüfbaren Programmcode zu schreiben. ↩︎